时序耦合约束下的多无人机协同任务决策研究

张耀中, 陈岚, 史国庆, 郭操

(1.西北工业大学 电子信息学院, 陕西 西安 710072; 2.沈阳飞机设计研究所, 辽宁 沈阳 110035)

无人机(unmanned aerial vehicle,UAV)具有隐身性好、自主能力强、可重回收等特点,能够代替有人机执行“枯燥、恶劣、危险”的任务,减少参战人员的伤亡,降低装备和使用成本等,其军事地位正不断提高,逐渐成为现代战场上的重要作战力量[1]。早期的无人机由于功能单一通常执行战场目标侦察、跟踪、监视等单类型任务,随着无人机平台以及各类载荷技术的快速发展,无人机的功能不断完善,任务能力不断增强,已经逐步转化为能够执行一系列复杂任务的多用途空中作战平台,如压制敌防空系统(suppression of enemy air defense,SEAD)、电子攻击、渗透式侦察/打击等任务。SEAD主要指对特定区域的敌方防空系统(预警雷达站、地面防空导弹雷达阵地以及通信/指挥控制站等)实施打击摧毁,使其暂时或永久失去作战能力,从而极大削弱敌方的防空力量[2]。

在SEAD作战任务中,假定每个目标都已事先侦察确认,则需要无人机分别对这些目标执行打击和毁伤评估2类子任务[3]。且打击任务完成后必须在特定的时间内执行相应的毁伤评估任务,因此这2类子任务间具有特定的时序耦合约束关系。

如何有效执行特定时序耦合约束下的多个任务已经成为当前无人机协同打击领域的研究热点问题之一。国内外的研究者提出了不少相应的解决方案,并取得了一定的成果,如文献[4]以多无人机协同执行搜索——打击任务为背景,提出了一种PTCFA联盟组建算法,在搜索到目标时,由leader组建针对该目标的打击联盟和毁伤评估联盟,同时满足相应的约束条件,是一种比较有效的分配方法,但是该算法对无人机资源约束做了较多的简化处理。文献[5]对集中式控制和分布式控制进行比较后认为当无人机执行相互约束性强的任务时,集中式控制往往能获得更好的性能。文献[6]同时考虑了多无人机的空间协同约束、任务执行时序约束和时间约束等多类协同约束关系,给出了求解策略,但算法搜索空间巨大,难以在有效时间寻找最优解。文献[7]考虑了单任务规划中的优先级约束,规定具有较低优先级的任务必须在具有较高优先级的任务执行之后才能被分配,但算法在考虑2种以上任务类型时的寻优时间随着任务的增多而呈指数增长,大规模动态任务规划难以实现。文献[8]采用分布式方法建立了具有时序约束的任务分配模型,将任务按优先级分层,运用扩展的一致性束算法进行求解,对比集中式算法,求解结果相对较差但可行。文献[9]针对多异构无人机协同任务规划问题构建了分层控制算法,在考虑无人机的异构性、资源有限性以及任务多样性等复杂约束条件下,针对任务中存在的死锁问题提出了一种基于图论算法的解锁方法,取得了较好的效果。

通过对相关文献的分析可以看出,目前对耦合约束特性下协同任务决策问题的研究已经取得了不少成果。但是由于任务间特定的耦合关系导致任务分配过程具有一定的复杂性,针对特定任务时序耦合下协同分配问题的研究仍然较少。本文通过研究多异构无人机协同执行SEAD任务过程中存在的时序耦合约束,提出了一种基于遗传算子的离散引力搜索算法(GSA-GA)对问题进行求解,通过仿真验证了算法的有效性,并采用蒙特卡罗仿真实验与离散粒子群算法(DPSO)进行了对比,仿真结果表明该算法具备更好的收敛性和更快的收敛速度。

1 具有时序耦合约束时的协同任务决策问题建模

1.1 问题描述

设有3种类型(约定为A/B/C型)共M架无人机,无人机配置信息如表1所示,用集合U={U1,U2,…,UM}表示。任务场景中有N个待摧毁目标,用集合T={T1,T2,…,TN}表示,要求无人机在任务航程最短约束下对所有目标执行打击和毁伤评估2种任务,要求目标必须在打击任务完成后的特定时间约束内完成相应的毁伤评估任务。

表1 无人机配置信息表

1.2 目标函数

在无人机执行SEAD任务时要求无人机在任务区内飞行的时间越短越好,因此,以最小化所有无人机中的最大任务航程为目标函数,定义如下:

F=min(maxVi)i=1,2,…M

(1)

式中,Vi表示第i架无人机的任务航程。i=1,2,…M为无人机编号。

假设无人机在任务执行过程中的飞行高度和速度恒定,则第i架无人机的航程为:

Vi=vi×(eTni-sTni)+D(Tni,BP)

(2)

式中,vi为第i架无人机的速度;eTni为任务Tni的完成时刻;sTni为任务Tni的开始执行时刻;D(Tni,BP)为任务Tni与基地BP的欧式距离,计算公式为:

(3)

xBP,yBP,xTni,yTni分别为基地BP与任务Tni的位置坐标。

(4)

pi表示第i架无人机的初始位置,Ti(ni-1,ni)表示第i架无人机从任务ni-1所在的位置飞向任务ni所在位置需要的时间,其计算公式为:

(5)

1.3 约束条件

时序耦合约束下协同任务决策问题中的约束条件如下:

1) 确保每个目标的打击和毁伤评估任务都能被执行:

(6)

(7)

Tjh为目标Tj的第h类任务(h=1,2),h=1表示打击任务,h=2表示毁伤评估任务。

2) 确保每个任务只能被执行1次:

(8)

3) 确保每架无人机至少被分配1个任务:

(9)

4) 满足任务执行的时序耦合约束:

sTjh+xijh*tijh≤eTjh

(10)

eTjh≤sTj(h+1)

(11)

tijh为无人机Ui执行任务Tjh的任务执行时间;sTjh表示任务Tjh的开始执行时刻,eTjh表示任务Tjh的完成时刻。

5) 航程约束:

Vi≤Vmaxi

(12)

Vmaxi为无人机Ui的最大航程。

6) 武器载荷资源约束:

(13)

Ri为无人机Ui携带的武器载荷数量。

7) 打击任务和毁伤评估任务的时序约束:

eTj1+Inter-min≤sTj2

(14)

eTj1+Inter-max≥sTj2

(15)

Inter-min和Inter-max分别为打击任务和毁伤评估任务间的最小和最大时间间隔。

2 基于遗传算子的混合引力搜索算法

2.1 引力搜索算法

引力搜索算法(gravitation search algorithm,GSA)是由克曼大学教授Esmat Rashidi等人在2009年提出的元启发式优化算法,其本质是模拟自然界中的万有引力现象,并将其演化成随机搜索最优解的过程[12]。GSA算法的原理如下:

1) 个体表示:

假设在一个D维搜索空间中,存在N个个体构成的群体,第i个个体的位置为:

(16)

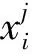
2) 质量计算:

每个个体的惯性质量由个体所在位置所决定的适应度值决定,在t时刻,个体Xi的质量用Mi(t)表示,计算公式如下:

(17)

式中,fi(t)表示个体Xi在t时刻的适应度值,b(t)和w(t)分别表示在第t次迭代中所有GSA个体的最好适应度值和最差适应度值。

3) 引力计算:

在t时刻,个体i和个体j之间在第l维的万有引力计算公式为:

(18)

式中,Mpi(t)表示在t时刻个体i的被动引力质量,Maj(t)表示在t时刻个体j的主动引力质量,s是防止分母为0的控制常量,Rij(t)为个体i和个体j在t时刻的距离。G(t)表示t时刻的引力常数,它由开始的某一初始值,随着时间的推移,迭代步数的增加不断地减小,其计算公式为:

(19)

式中,T表示最大迭代次数,G0和α为固定常数。参考文献[13],通过多次试验数据表明G0取100,α取20时算法具有最好的收敛性能。

Rij(t)表示个体i和个体j在t时刻的距离:

Rij(t)=‖Xi(t),Xj(t)‖

(20)

式中,Xi(t)和Xj(t)分别为个体i和个体j在t时刻的位置。而在t时刻,个体i在第l维上受到的合力等于其他所有个体对其作用力的总和,计算公式如下:

(21)

4) 位置更新:

引力搜索算法来源于对万有引力现象的模拟,它遵循经典的牛顿第二定律。当个体受到其他个体的引力作用后会产生相应的加速度,因此,根据公式(20)计算得到的引力以及牛顿第二定律,个体i在第l维获得的加速度等于其受到合力与其自身惯性质量的比值,计算公式为:

(22)

式中,Mii(t)为个体i在t时刻的惯性质量,其值等于(17)式中的Mi(t)。

每一次更新过程中,个体根据引力产生的加速度更新自身的速度和位置,更新方式如公式(22)所示:

(23)

2.2 个体编码模式

针对问题特点,我们采用了一个4N维的数组表示一个个体,分为2部分:任务分配(task allocation)部分和任务排序(task sequencing)部分,其中个体的前2N维为任务分配部分,余下2N维表示任务的排序方式。

任务分配部分表示了N个目标共2N个任务的分配结果,即哪个目标的哪个任务分配给哪架UAV。该部分共有2N个位,由N个目标依次按照目标编号排列,从第一个位开始,每两个位代表一个目标,其中第一个位表示攻击任务,第二个位表示毁伤评估任务。每个位的取值为当前位所代表任务可供选择的UAV顺序编号,有效保证了各任务被分配给能够执行该任务的UAV。

任务排序部分表示了所有任务的排序情况,由2N个位组成,每个位由目标的编号编码,每个目标的编号出现2次,出现的顺序表示该目标两个任务间的先后顺序,目标编号i出现的第j次,表示该目标的第j个任务。设定j=1表示攻击任务,j=2表示毁伤评估任务。如此编码,可保证攻击任务和毁伤评估任务的时序耦合约束。

2.3 个体解码模式

个体信息的解码是在编码的基础上,采用相反的处理模式,将编码得到的数据通过一定的方式转换成所求解问题的可行解决方案,用解码得到的数据计算出当前方案的适应度值,即目标函数值,并通过目标函数值的大小评判当前解决方案的优劣。

算法的具体解码步骤如下:

Step1 对个体的任务分配部分进行解码。

1) 初始化各无人机的任务集合为空集,即Tsequencei=ø;

2) 从左至右依次读取第k位上的值i,若k为奇数,则j=(k+1)/2,h=1;若k为偶数,则j=k/2,h=2,将Tjh加入到Tsequencei中。

Step2 对个体的任务排序部分进行解码。

1) 从左至右依次读取第k位上的值j,每个j代表的是目标Tj上的一个任务,若j是第h次出现,则表示Tjh。当k=2N得到所有任务的排列顺序Ts;

2) 将Tsequencei根据Ts重新排列任务顺序,当Tjh和Tkl都在Tsequencei中时,将两者按照Ts中的先后顺序重新排列。

Step3 输出各无人机的任务执行序列Tsequencei。

2.4 种群初始化与个体更新策略

以随机数方法对每个个体进行初始信息赋值。对于个体中的任务分配部分通过(23)式更新个体的位置和速度,更新后的个体位置需要进行可行性修正。首先对每一位的值采用四舍五入的方法进行取整,其次,对取整后的每一位进行合法性判断,若该位的取值不在该位表示任务的可执行无人机集合内,则采用就近原则,以集合的边界元素代替。

对于任务排序部分的更新,本文引入遗传算法中的交叉和变异操作对该部分进行更新。

1) 交叉:交叉操作是利用父代个体经过一定的操作组合后产生新个体,从而达到在不破坏有效模式的前提下对解空间进行高效搜索的目的。采用改进的POX交叉方法,对个体的任务排序部分进行交叉操作,进而达到更新的目的。改进后的POX交叉操作每一次只产生一个新个体,算法步骤如下:Step1:从目标集{T1,T2,…Tn}随机抽取一个目标子集Tset;

Step2 选择需要进行交叉操作的个体X1和X2,若X1的适应度函数优于X2,则将X1中包含在目标子集Tset中的目标复制到新的个体C中,保持位置和顺序不变;

Setp3 将X2中不包含在Tset中的目标复制到C中,保持顺序不变;

Step4 若新个体C的适应度函数优于X2,则保存新个体,并替代原来的个体X2。如图1所示,含有4个目标,随机抽取的目标集Tset={2,3},X1要优于X2,将X1中包含目标2,3的位复制到新个体C中,然后将X2中去掉目标2,3后,剩下的部分按照原来的次序依次复制到C的除去2,3所在位的其他位,从而产生新个体C。

图1 POX交叉操作

2) 变异:变异操作是通过随机改变个体的某些位,从而产生较小扰动生成新个体,增加种群多样性,在一定程度上控制引力搜索算法的局部搜索能力。我们采用基于邻域搜索变异操作,在个体的任务分配部分不变的情况下,采用基于邻域搜索的变异方法,能够更好地通过局部范围内的搜索找到适合任务分配部分的任务排序,从而改善子代性能。其算法操作步骤如下:

Step1 在个体的任务排序部分随机选择r个位,并生成其排序的所有邻域;

Step2 计算所有邻域的适应度函数值,选出最佳个体作为子代,并代替原来的个体。

引入遗传算子改进后的混合引力遗传搜索算法(GSA-GA)的处理流程如图2所示。

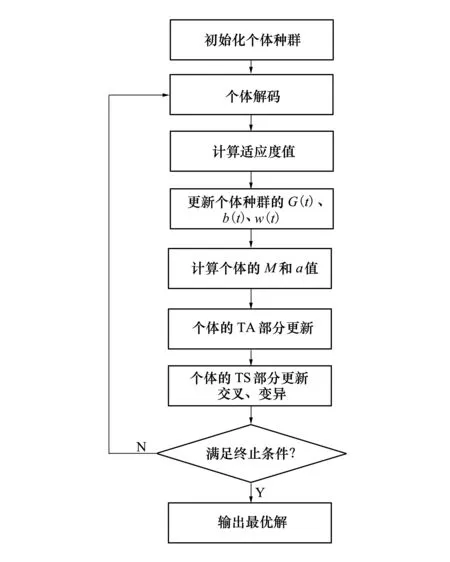
图2 GSA-GA算法流程图

3 仿真算例与分析

设定任务场景中有5架UAV和9个待摧毁目标,无人机相关信息如表2所示。

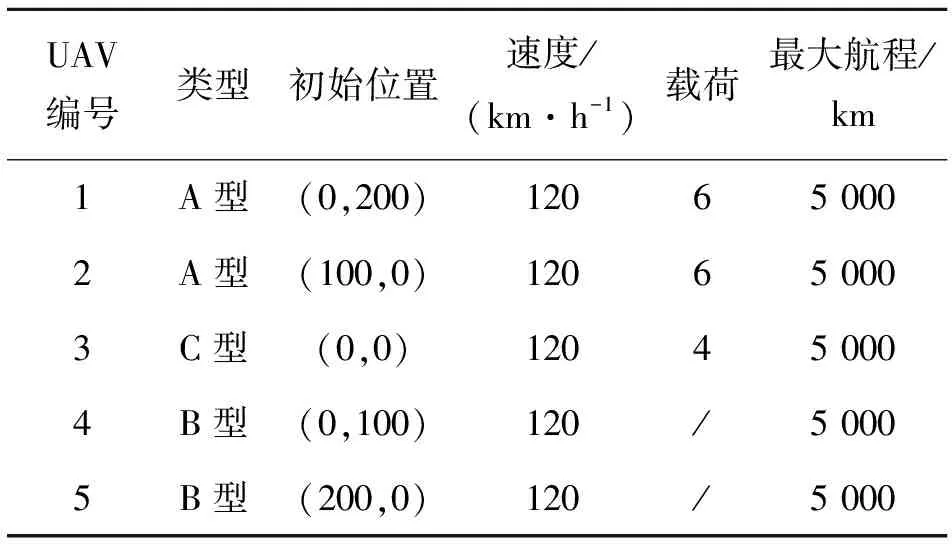
表2 无人机相关信息

目标及返回基地信息如表3所示。假设无人机执行完成打击任务的时间为0.05 h,执行完成毁伤评估任务的时间为0.1 h,且毁伤评估任务和打击任务的最小时间间隔为0.1 h,最大时间间隔不能超过0.5 h。

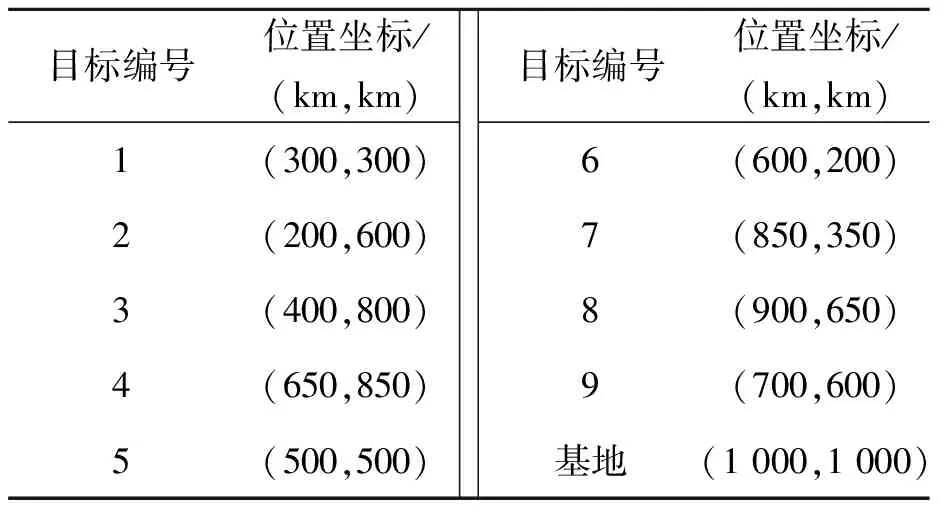
表3 目标及基地位置信息

基于以上作战想定,采用改进的引力搜索算法进行仿真,种群规模为30,最大迭代次数为100次。仿真得到最优任务分配结果如表4所示,各子任务被执行时刻如表5所示,图3为最优任务分配结果下的无人机执行任务过程示意图。

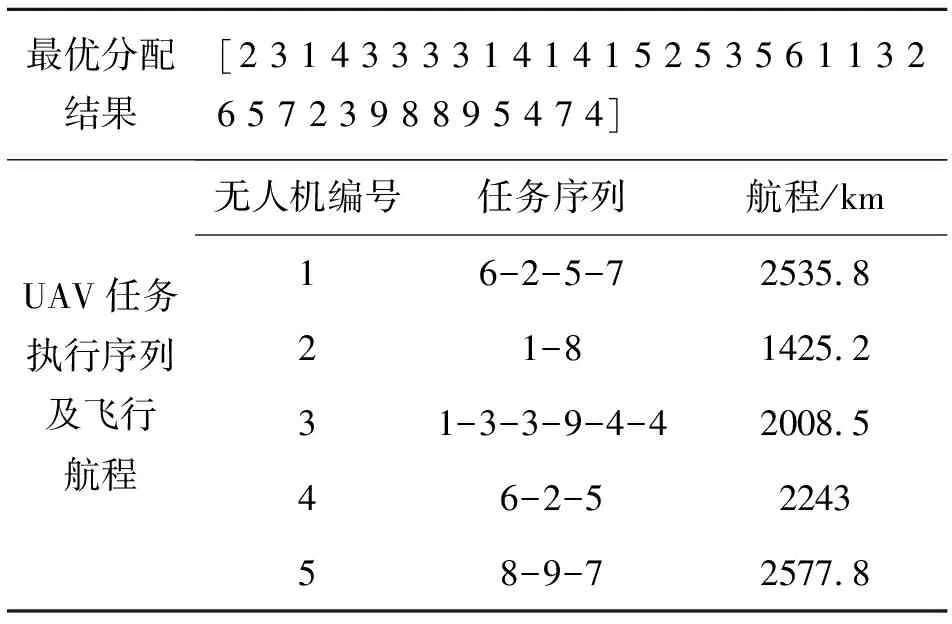
表4 最优分配结果

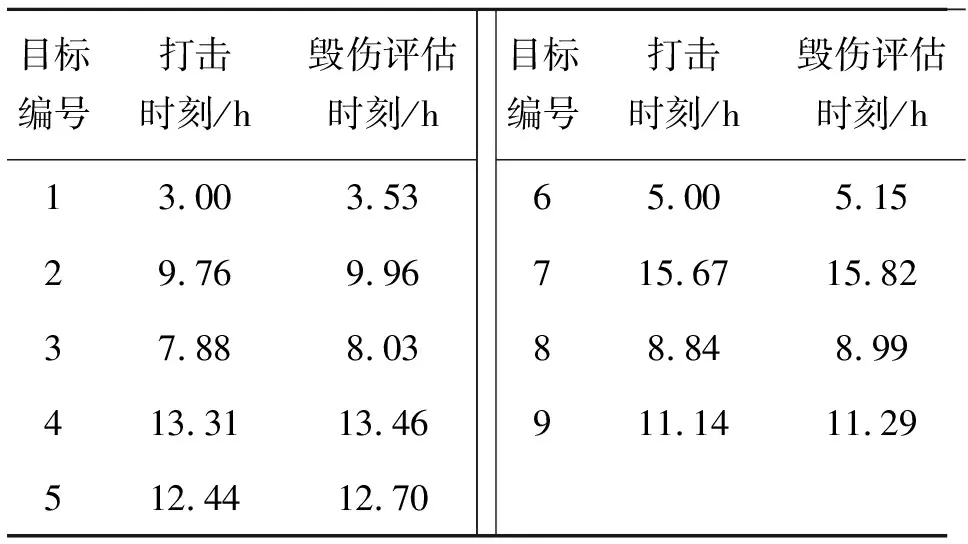
表5 任务执行时刻表

由表4可以看出,分配结果中各UAV的资源约束和航程约束是完全满足的,由表5可以看出,各目标的打击与评估任务是满足任务间的时间耦合约束的。

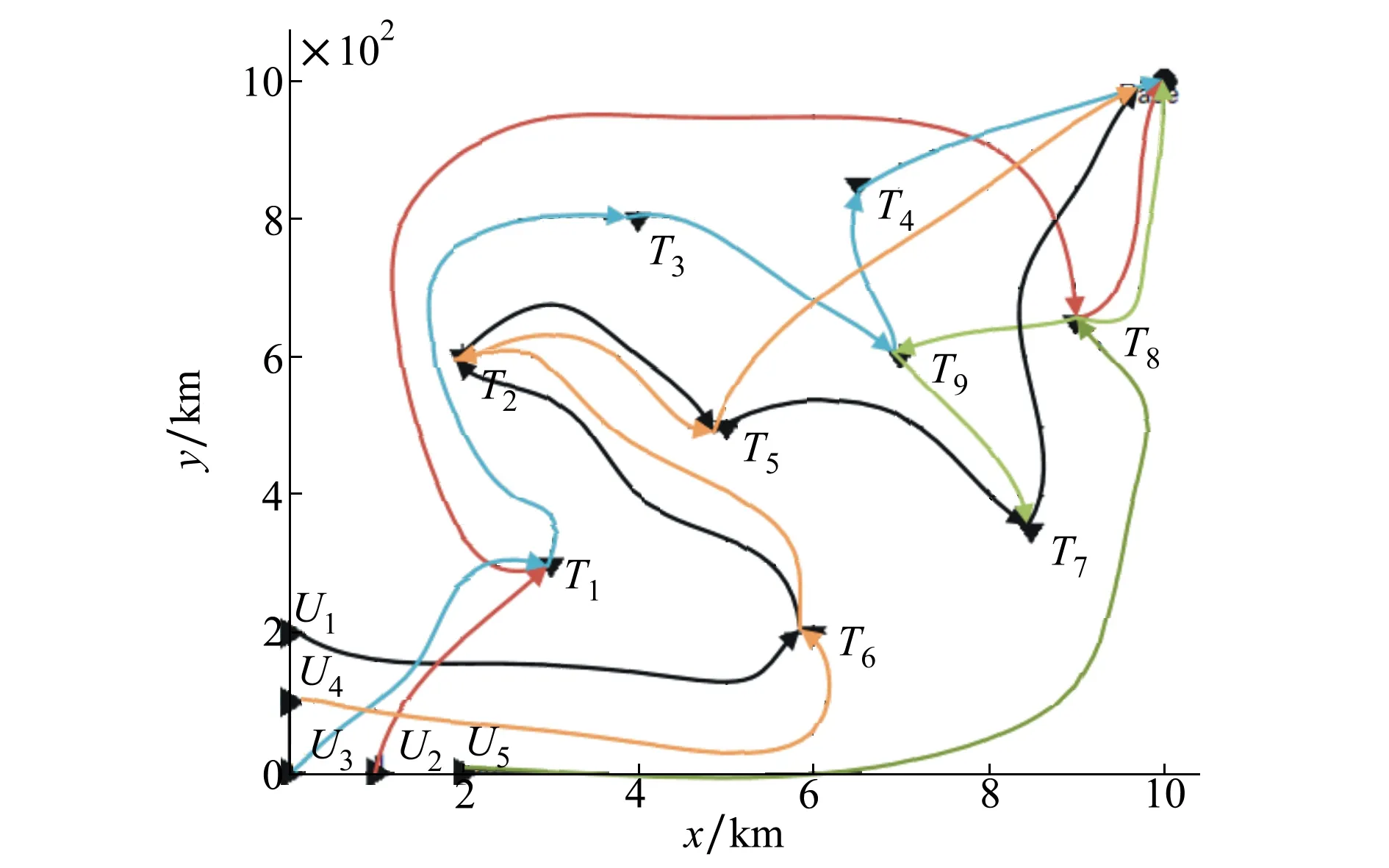
图3 无人机执行任务过程示意图

为了验证GSA-GA算法的性能,针对上述问题,采用离散粒子群算法(DPSO)进行仿真对比分析,DPSO参数参照文献[11]设置为:粒子种群规模为30,最大迭代次数为100,ω=0.5,c1=0.3,c2=0.2,图4所示为2种算法求解下的收敛曲线。由图中可以看出,相对于DPSO算法,改进的引力搜索算法能够较快地收敛到最优解。但是由于2种算法均属于启发式优化算法,求得的结果往往不一定是最优解,也可能是次优解,因而单一的仿真结果并不能准确地比较出2种算法在求解任务分配问题上的优劣,针对以上问题分别采用2种算法进行200次蒙特卡罗法仿真实验,2种算法的收敛过程如图4所示,统计结果如表6所示。

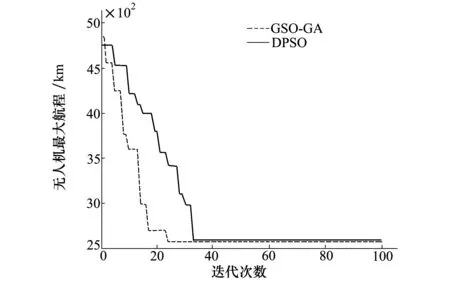
图4 GSA-GA和DPSO的收敛曲线

表6 GSA-GA与DPSO算法对比分析

如表6所示,经过200次随机求解,改进的GSA-GA算法得到的最佳适应度为2 577.8,最差适应度为2 720.5,平均适应度为2 585.9 km,平均收敛代数为20代,平均消耗时间为1.073 s,相比于DPSO算法,在最佳适应度、平均收敛代数及平均消耗时间上均有更好的表现。实验数据表明,改进的GSA-GA算法能够更高效地对时序耦合约束下多UAV协同任务决策问题进行求解。

4 结 论

多无人机协同任务决策问题是一个十分复杂的典型NP-Hard问题,本文以多无人机协同执行SEAD任务为背景,重点关注任务间的时序耦合关系,对时序耦合约束下的多无人机任务分配问题进行了数学建模,提出了一种基于遗传算子的混合引力遗传搜索算法 (GSA-GA)并应用于任务分配问题的求解,通过算例仿真实验验证了所提出算法的有效性和合理性,并采用蒙特卡罗仿真方法对改进算法与离散粒子群算法进行了对比分析,结果表明GSA-GA 算法能够更快地收敛,寻优结果更优。从而为无人机执行具有时序耦合约束任务时的协同任务分配问题提供了科学的决策依据。