嵌入式多核系统中三维立体调度模型的研究
黄姝娟, 朱怡安, 刘白林, 肖锋
(1.西安工业大学 计算机科学与工程学院, 陕西 西安 710021; 2.西北工业大学 计算机学院, 陕西 西安 710072)
嵌入式多核平台下,任务调度是系统的核心,如何优化调度算法,充分发挥多核处理器性能优势,是当今研究的主要方向[1-3]。当前多核实时任务的调度算法主要分为全局调度算法(global scheduling algorithm)[4-6]和分区调度算法(partitioned scheduling algorithm)[7-8]2大类。GEDF(global earliest deadline first)[9]和PEDF(partitioned earliest deadline first)[10],是2类调度算法的典型代表。对于全局调度算法来说,如果一个任务不允许抢占,而另外一个任务必须执行,那么就要将该任务迁移到其他核上执行[11]。这种迁移开销比较大。对于分区调度算法而言,划分在一个范围内的任务只能在同一个处理器核上调度,虽避免了迁移,简化了问题[12],但对划分的精确度有很高要求,划分不好会直接影响丢失时限的任务数量。很多情况下任务划分方法是很棘手的问题。为此,研究者提出了半分区调度算法(semi-partitioned scheduling algorithm)[13],该方法将全局调度算法与分区调度算法相结合,旨在减少迁移开销的同时减少进行划分的任务数量,降低划分难度。尽管如此,该类算法仍然存在迁移开销和划分方法如何精确的问题。为此,本文提出一种三维立体调度模型和调度算法,该方法以区域面积作为划分方法,降低划分的难度,提高划分算法的精确度,在提高系统效率的同时,降低丢失时限的任务数量。
1 三维调度模型
1.1 实时周期任务模型
假设一个包含n个实时周期任务的嵌入式多核系统I={T0,T1,T2…Tn},其中Ti为一个四元组Ti(Ri,Ci,Di,Pi),Ri表示该任务首次发布时刻,Ci表示该任务的WCET(worst case execution time),Di表示相对时限且Di≥Ci,Pi表示该任务的执行周期且Pi≥Di≥Ci。用Jobi,j(ri,j,ci,j,di,j)表示Ti的第j次执行,其中ri,j为jobi,j的发布时间ri,j=Ri+(j-1)Pi,ci,j为jobi,j的执行时间ci,j=Ci,di,j为jobi,j的绝对时限di,j=ri,j+Di=Ri+(j-1)Pi+Di。
1.2 三维调度模型
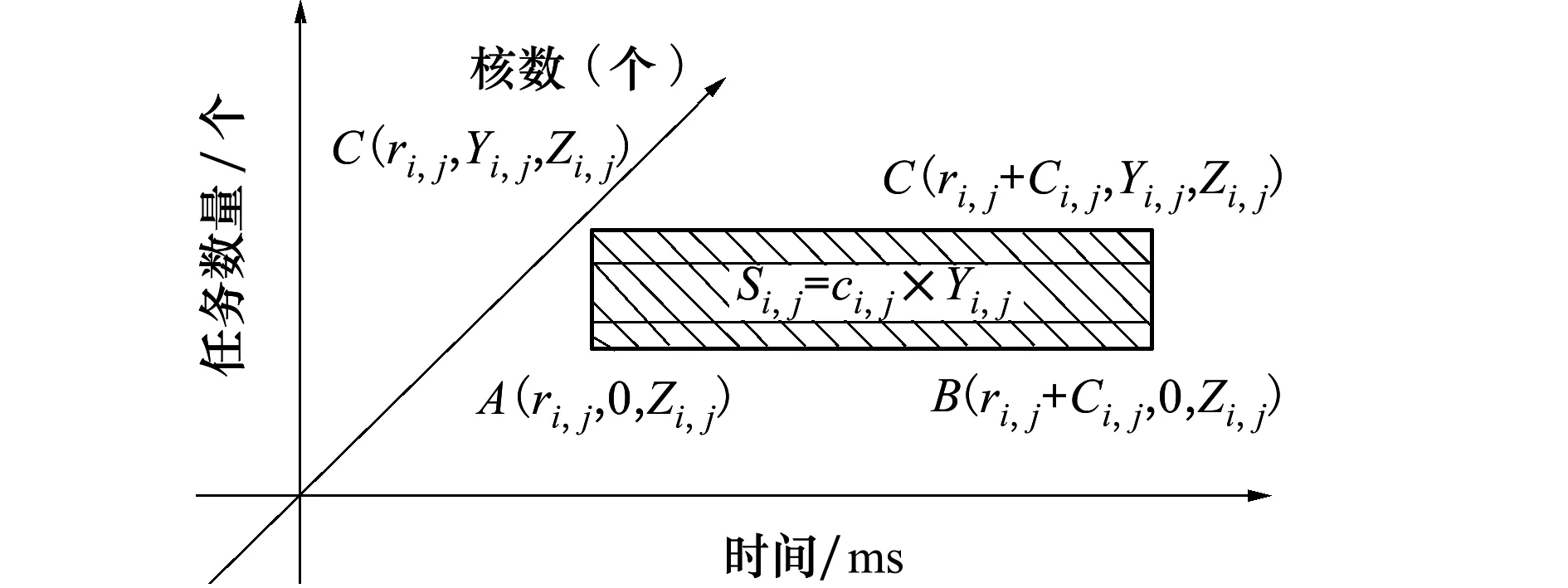
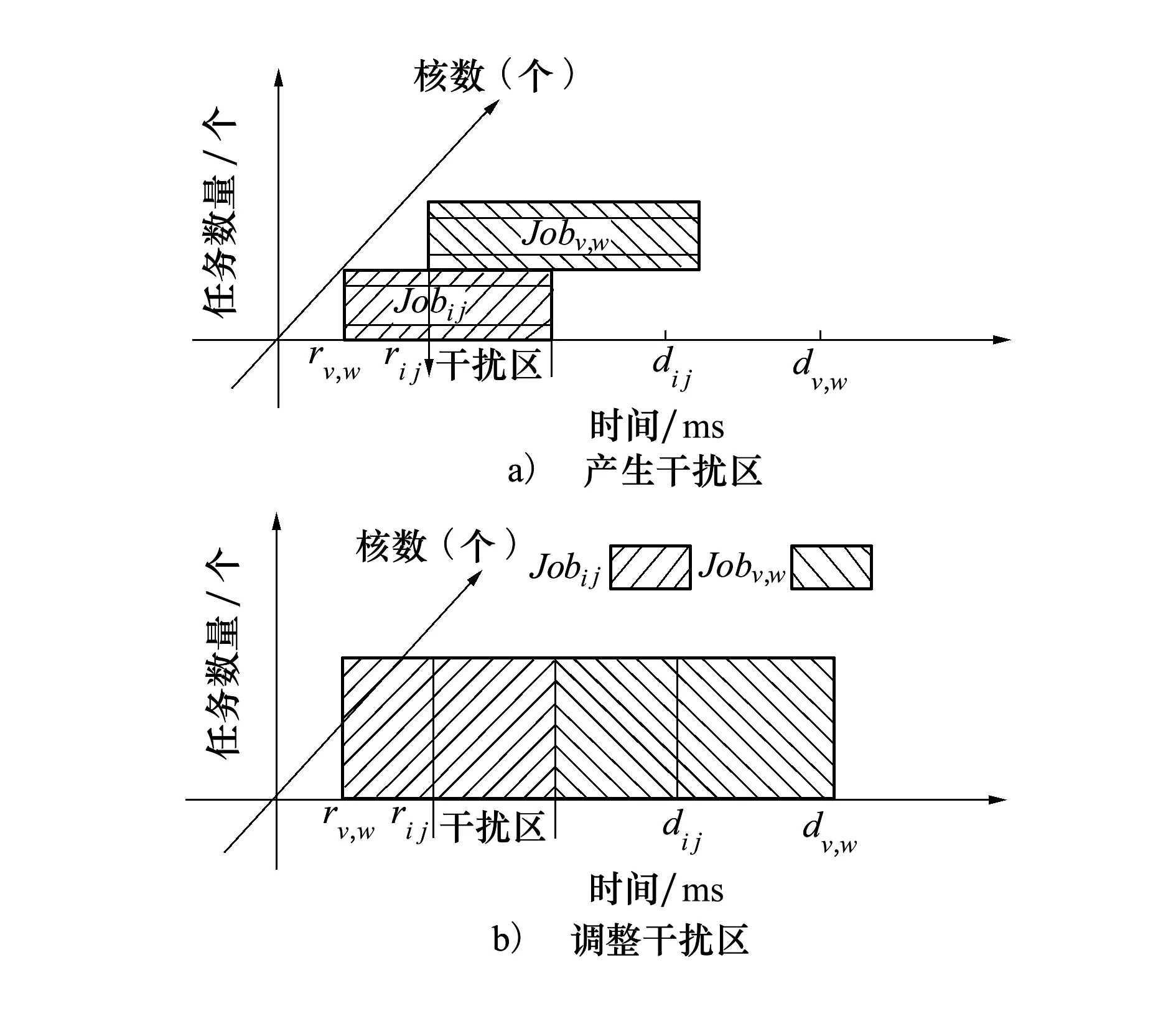
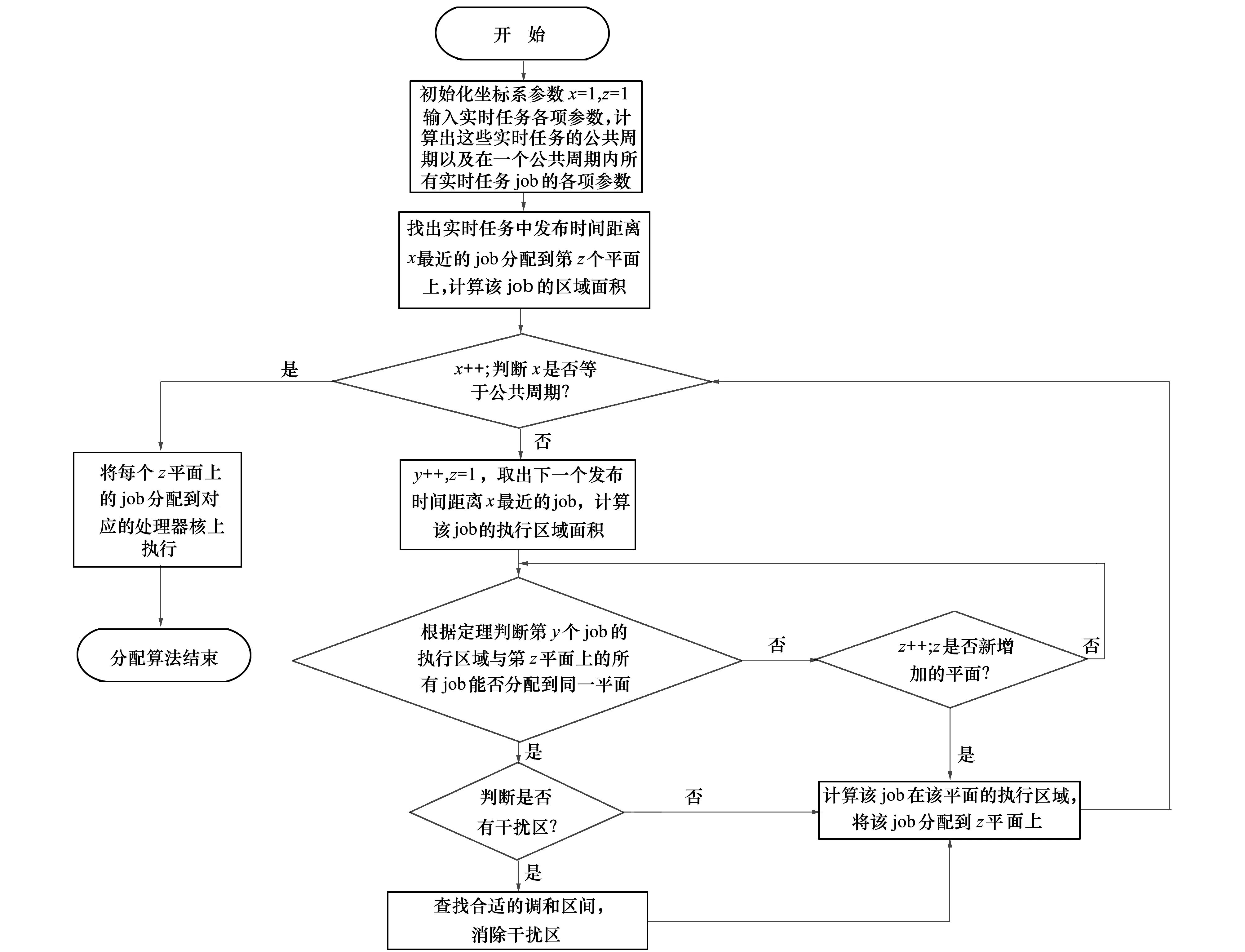
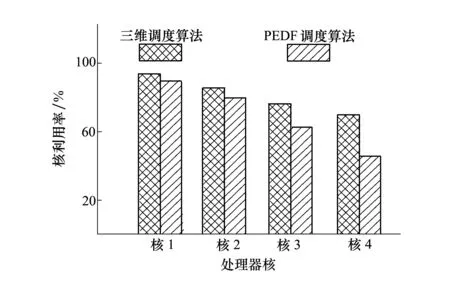
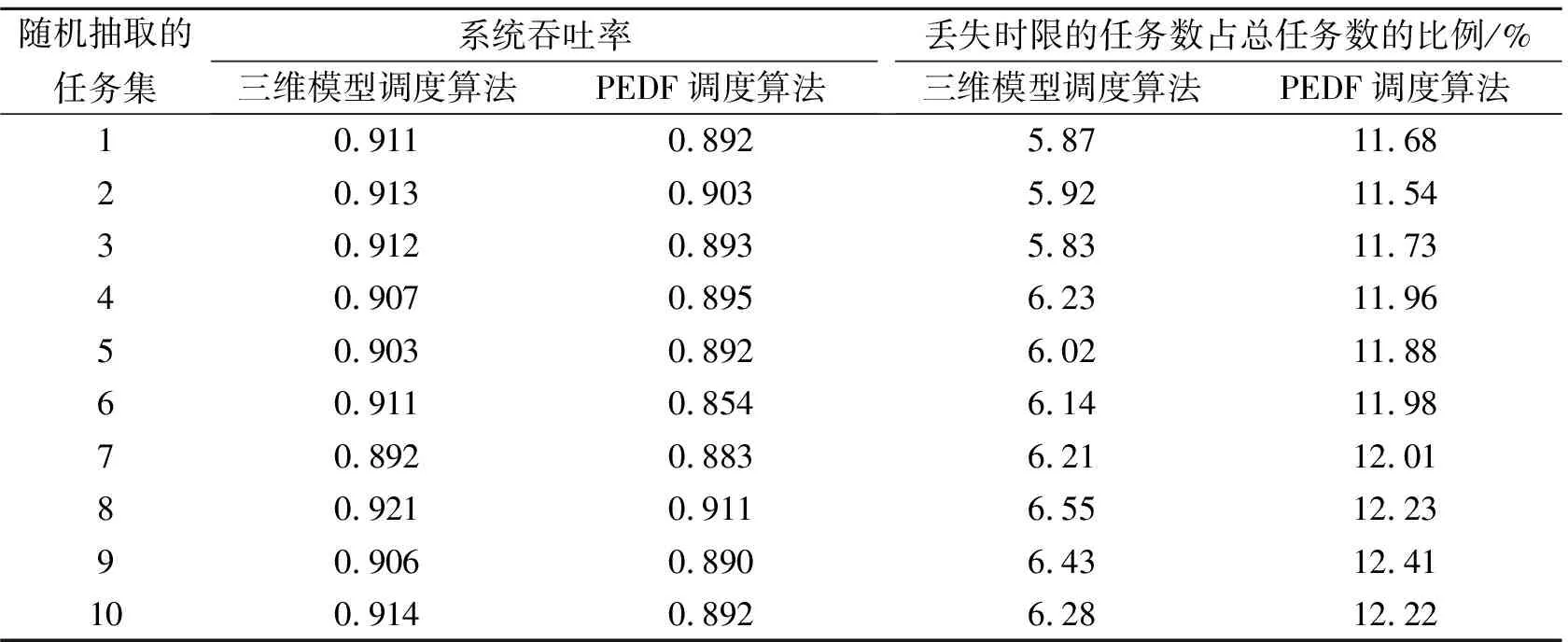
定义1对于一个实时周期任务Ti(Ri,Ci,Di,Pi),如果Ci=Di则称该任务为不可调和任务;如果Ci 定义2对于一个可调和任务Ti(Ri,Ci,Di,Pi),若用hfi表示该任务的调和因子(harmonic factor),则hfi=Di-Ci。则Ti的任何一个jobi,j都会有hfi+1个调和区间HFi,j={[ri,j+k,ri,j+ci,j+k]| 定义3对于任意实时调度系统I={T0,T1,T2…Tn},必然存在一个三维调度空间Ω={x,y,z},其中x表示时间轴,y表示当前运行在该平面的任务数,z表示处理器核数。对于任何一个实时周期任务Ti的任何一次执行jobi,j,该调度空间上必然会存在该job执行的一个矩形区域Φi,j,该区域的4个顶点坐标分别为Ai,j(ri,j,0,zi,j),Bi,j(ri,j+ci,j,0,zi,j)Ci,j(ri,j,yi,j,zi,j),Di,j(ri,j+ci,j,yi,j,zi,j)其中zi,j表示给jobi,j分配的处理器号,yi,j表示在第zi,j平面上所分配的任务的个数;把该矩形区域Φi,j称为jobi,j对应在该三维调度空间Ω上的执行区域,简单记为Φi,j={(ri,j,ri,j+ci,j,yi,j,zi,j)}。 对应于该矩形Φi,j区域上的面积称为执行区域面积即Si,j=ci,j*yi,j如图1所示。 图1 Jobi,j(ri,j,ci,j,di,j) 的执行区域 定义4对于在同一Z平面上任何2个jobi,j和jobv,w,如果它们的执行区域面积没有任何交叉覆盖情况,则称jobi,j和jobv,w相互独立。如果在某段时间t内,2个任务Ti和Tj在该时间段内所有需要执行的job都相互独立,则称这2个任务在时间段t内相互独立。如果t为无穷大都能满足,则Ti和Tj称为永久相互独立任务。 定义5对于任何2个jobi,j和jobv,w的执行区域面积存在交叉覆盖情况,则称这2个job具有互干扰性。交叉覆盖的区域称为干扰区。相对应的干扰区面积SΛ为交叉覆盖面积,相对应的jobi,j对jobv,w的干扰因子为ξi,j/v,w=SΛ/Sv,w而相对应的jobv,w对jobi,j的干扰因子为ξv,w/i,j=SΛ/Si,j。 定义6对于任何2个具有干扰区的job,如果至少有一个是可调和job,且其衍生出来的任意一个job或者是l-job中存在执行区域与另外一个job或其任意一个衍生job或者是l-job相互独立,则称这干扰区为可调和干扰区,否则称为不可调和干扰区。 定义7k重干扰区 如果在某段时间t内,存在k个job的执行区都覆盖了同一干扰区且该干扰区对于任何一个job都不可调和,那么称该干扰区为k重干扰区。 定义8如果在Z=zi平面上存在某个区域既不是执行区也不是干扰区,则该区域称为闲置区。 定义9给定一个三维空间Ω={x,y,z}在某段时间t内,假设xt,yt和zt分别为三维空间在该时间段内3个坐标轴所能取到的最大值,则在任意的Z=zi(i=1,2,…t)的平面内,所有单位面积之和称为可调度空间面积,记为S=xt*yt。 由上述定义可知,调度空间面积为执行区面积和闲置区面积之和。对于Z=zi的平面,任何一个区域无非为干扰区、执行区和闲置区三者之一,其中干扰区必定是执行区。 推论1如果系统I中所有任务之间在任何时间段不产生不可调和干扰区,则该系统中所有任务可以被调度在同一个处理器上。 证:如果在任何时间段内不产生干扰区,就说明所有任务都有自己的执行区且执行区并不被相互覆盖,那么所有任务在任何时间段内产生的job都能在时限之前被调度完成。故可以被分配到同一个处理器上。 如果在任何时间段内产生的干扰区都是可调和干扰区,就说明所有任务都有自己的执行区且执行区通过调和区间衍生job或者l-job调和后并不被相互覆盖,那么所有任务在任何时间段内产生的job都能在时限之前被调度完成。故可以被分配到同一个处理器上。 推论2若在某段时间t内,系统I产生k重干扰区,则在该时间段内必须有k个处理器核才能完成调度。 证:因为产生了k重干扰区,说明有k个job的执行区域都覆盖在同一区域,且没有任何可调和空间,若采用小于k个处理器核来调度,则必然还会产生无法调和的干扰区,一定会存在一些job无法在时限之前调度完成,因此必须采用k个处理器核来调度。 可以根据区域覆盖情况来判断2个job是否有干扰区。如果任务是可以互相抢占的,可以根据任务的可调和性来判断干扰区是否为不可调和干扰区。下面讨论都是可抢占的实时任务。 定理假设在不考虑上下文切换和中断等额外开销的情况下,任何2个jobi,j(ri,j,ci,j,di,j)和jobv,w(rv,w,cv,w,dv,w)能够被调度在同一平面z上的充分必要条件是区域Φ={min(ri,j,rv,w),max(di,j,dv,w),2,z}的面积大于等于jobi,j的执行区域面积与jobv,w的执行区域面积之和。 证明先证充分条件: jobi,j(ri,j,ci,j,di,j)和jobv,w(rv,w,cv,w,dv,w)的ri,j,rv,w,di,j,dv,w有如下4种情况:①ri,j≤rv,w且di,j≤dv,w;②ri,j>rv,w且di,j>dv,w;③ri,j>rv,w且di,j≤dv,w;④ri,j≤rv,w且di,j>dv,w 先证明(1)因为dv,w-ri,j≥dv,w-rv,w≥cv,w且di,j-rv,w≥di,j-ri,j≥ci,j那么由条件知Φ={(ri,j,dv,w,2,z)}的区域面积S=(dv,w-ri,j)×2≥Si,j+Sv,w其中Si,j=ci,j×2;Sv,w=cv,w×2分别是jobi,j和jobv,w的执行面积,如果没有干扰区,则根据推论1在时间段[ri,j,dv,w]内jobi,j和jobv,w可以调度在同一个处理器核上。若有干扰区如图2a)所示,则可以在Ω中先满足jobi,j的执行区域,保证jobi,j在di,j之前执行完毕。剩余的区域划出与Sv,w等量的区域作为jobv,w的执行区域,则能保证jobv,w在dv,w之前完成,如图2b)所示。那么jobi,j和jobv,w就可以调度在同一个处理器核上。 图2 干扰区产生/调整图 同理可以证明②③④。 证明必要条件 根据推论1可知,如果可以调度在同一个处理器上则说明不存在干扰区或存在可调和的干扰区,如果不存在干扰区,则在[min(ri,j,rv,w),max(di,j,dv,w)]的时间段内Jobi,j和Jobv,w的执行区不存在区域覆盖的情况,则Jobi,j和Jobv,w的执行区域面积之和必定小于等于Φ={min(ri,j,rv,w),max(di,j,dv,w),2,z}的区域面积。 如果存在的是可调和干扰区,则可以通过调和区间在时间段[min(ri,j,rv,w),max(di,j,dv,w)]内化解为不互相覆盖的区域,则它们的执行区必定存在该时间段的区域内,Jobi,j和Jobv,w的执行区域面积之和必定小于等于Φ={min(ri,j,rv,w),max(di,j,dv,w),2,z}的区域面积。 得证。 本文所涉及的分区调度算法是根据实时任务的各项参数特征,计算出所有实时任务的公共周期。在该公共周期内找出实时任务所要执行的job。由文献[8]可以知道,如果该系统所有实时任务的job在公共周期内可以被调度成功,那么这些实时任务在所有周期内都能被调度成功。 系统开始初始化x,y,z3个参数代表3个坐标轴,分别表示时间、任务个数以及处理器个数;第一次找出发布时间最近的1个job分配到z=1的平面上,按照定义3计算出该job的执行区域,再依次找出相应的job,根据定理和推论3从z=1的平面开始判断新加入的job是否能被调度到该平面上,直到将所有新加入的job分配到相应的平面上,程序结束。具体算法流程图如图3所示。 图3 三维调度算法主流程图 在整个流程中,比较难的步骤是如何找出相应的调和区间以便消除干扰区。 方法如下: 1) 从该平面找出所有可调和job和不可调和job分别放入不同的队列中,将不可调和任务的执行区间放入集合H中; 2) 判断可调和队列是否为空?若是,则返回集合H。若不是,则转入步骤3)。 3) 从可调和任务队列中取出时限最小的job,从该job的可调和区间找出一个与集合H中的所有执行区间不覆盖的可调和区间,放入集合H中;转2。 具体算法流程如图4所示。 图4 查找合适的调和区间算法流程图 本文测试的环境是在一个Intel(R)Core(TM)2Quad Q8400多核平台上。将所提出的三维调度算法和PEDF算法进行比较,测试方法是随机产生1 000个任务集,每个任务集中产生50个参数不等的实时周期任务,所有周期任务都满足时限小于或等于周期,且执行时间小于时限。在整个仿真实验过程中,为了描述算法之间的性能差异,采用多次模拟求平均值的方法按照在某段时间内,系统吞吐率,丢失时限的任务数量所占总任务数的比例,核利用率3个方面进行性能对比,如图5和表1所示。 图5 2种算法核利用率 表1 2种算法的系统利用率和丢失时限任务数所占总任务的比例 从图5中可以看出,随着核数的增加,采用三维调度算法比PEDF算法在核利用率方面要更加充分。从表1可以看出,在系统吞吐率方面三维调度算法相比PEDF算法优势不是很明显。这是因为寻找调和区花费的时间比较长,开销较大,但在丢失时限的任务数比例方面,三维调度算法明显占据优势。这种提高对于解决减少丢失时限的任务数量来说,是能够满足某些实际需要的。由于目前实验条件限制,运行的核数量仅为4个,以后将在核数更多的机器上进行实验,并会进一步优化寻找调和区的算法,来验证三维调度算法的优势。 本文设计了一种新的三维调度模型,在该模型中确立了任务之间的相互独立和相互干扰关系,并根据调度面积设定了调度方案,给出了相应的调度算法。通过实验,该算法在核利用率、系统吞吐量以及丢失时限的任务数方面更优于PEDF算法。这为以后在异构多核平台下的实时任务调度提供了新的思路。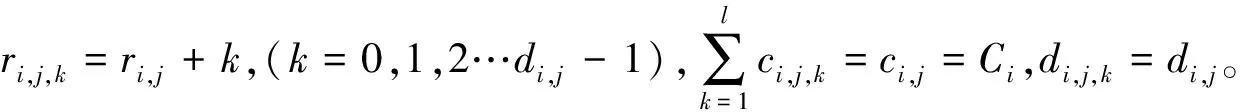
1.3 可调度性证明

2 调度算法

3 实验结果
4 结 论

