人口老龄化与收入不平等的时变效应
孙 晔,吕康银,朱金霞
(1.东北师范大学 商学院,吉林 长春 130117; 2.鲁东大学 商学院,山东 烟台 264025)
一、引 言
随着我国人口老龄化问题的凸显,其与收入不平等之间的动态关系已经成为学术界研究的热点之一,并且涌现出大量的相关研究文献。作为我国经济社会发展中日益凸显的两大焦点问题,二者之间究竟存在着怎样的关系,值得进行深入的理论研究与探索。
在实证研究方法上,可以将对该问题的研究分为基于线性模型的实证研究 (主要包括线性单方程回归模型、协整分析、线性Granger因果检验、线性向量自回归模型和线性面板回归模型等) 和基于非线性模型实证研究 (主要包括门限的单方程回归、滚动视窗Granger因果关系检验、面板平滑迁移回归模型等)。本文结合已有的研究思路,重点基于时域视角,使用含断点的时变协整、线性Granger因果关系检验、非线性Granger因果关系检验法考察我国老龄化与收入不平等之间的时变的动态关联机制,并进一步采用平滑迁移性向量自回归模型 (STVAR) 检验二者之间是否存在非对称的影响及测度影响效果。
二、数据选取与处理
对于收入不平等的度量,已有研究文献使用最多的指标是基尼系数 (董志强等,2012[1];刘金东等,2014[2];蓝嘉俊等,2014[3];范洪敏和穆怀中,2018[4])。鉴于此,本文选择我国基尼系数作为收入不平等的度量指标,记为Gini。对于老龄化的度量,存在大量的选择空间,比如采用老年抚养比和少儿抚养比构造度量老龄化的指标*老龄化=老年抚养比/ (1+老年抚养比+少儿抚养比),具体参见蓝嘉俊等 (2014)。和采用老年抚养比*65岁 (含65岁) 以上老年人口占15~64岁劳动年龄人口的比重。度量老龄化。本文参考范洪敏和穆怀中 (2018)[4]的做法,选择老年抚养比作为老龄化的代理变量,记为Aging。以上基尼系数原数据和老龄化原数据均来自于WIND数据库,二者具体的实际序列如图1、图2所示。
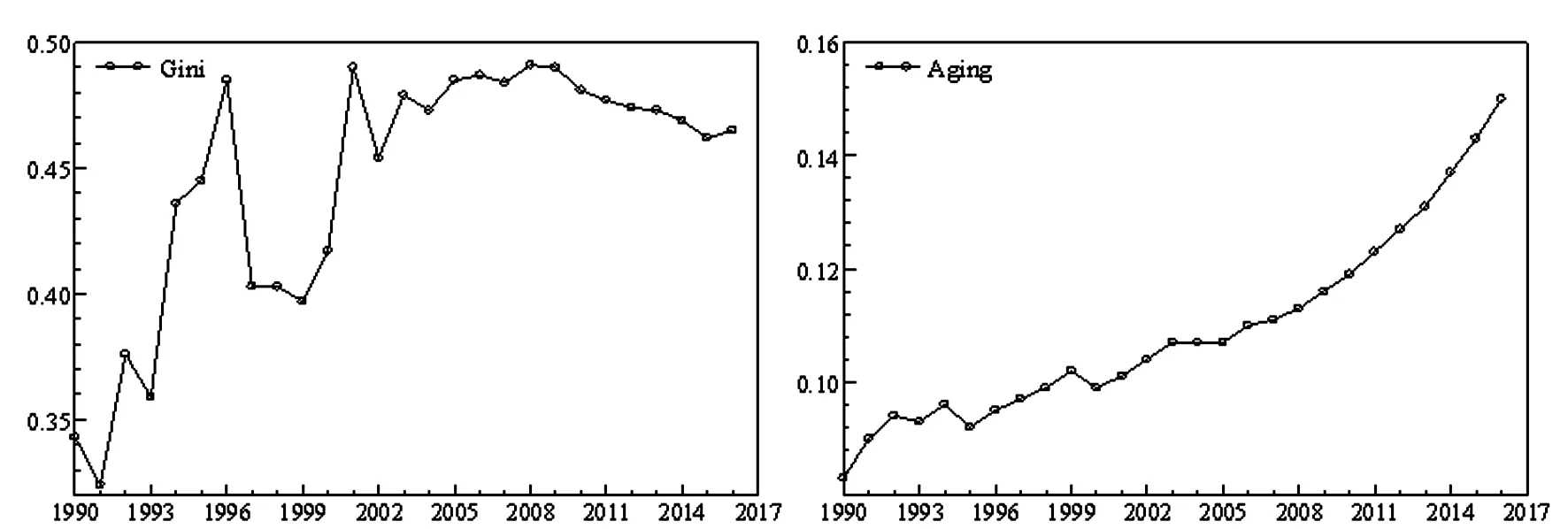
图1 中国基尼系数序列 图2 中国老龄化序列
从图1、图2中绘制的原始数据序列可以看出我国基尼系数和老龄化之间在整体上存在缓慢的上升趋势,即可能存在某一协整向量可以较好拟合二者间的长期相关关系;但在局部时间内二者之间的协同性较差,具体表现在1990年至1999年间,基尼系数呈现出陡增骤降的特征,而此时的老龄化序列却表现出具有较小波动且逐渐上升的特点;此外,在1999年之后基尼系数出现急剧上涨并持续保持较高的水平,相对应的老龄化序列表现出稳健上升的态势。
结合两段时间内每个时间序列变量均表现出独自特点的现象,从统计学角度出发,二者可能存在时变的协整关系,而此时如果采用常系数协整检验方法可能有失准确性和稳健性。有鉴于此,本文主要的研究思路是首先检验二者是否具有时变的协整关系;其次基于检验结果通过构建线性Granger因果关系检验和非线性Granger因果关系检验法进一步确定二者之间的交互影响关系,即确定二者间的因果关系。
三、我国收入不平等与老龄化的时变协整检验
基于图1和图2的描述,由于我国收入不平等与老龄化均在样本期间表现出各自的特征,二者之间可能存在时变的协整关系,因此,需要构造时变协整检验模型来考察二者之间的长期关系是否稳定。众所周知,协整检验是建立在变量均是同阶单整序列基础上的,因而在构建时变协整模型前应对时间序列数据进行平稳性检验。
(一)数据平稳性检验
为了与数据选取中所标记的符号一致,在数据平稳性检验中我们将基尼系数序列(Gini) 和老龄化序列(Aging)的一阶差分分别标记为△Gini和△Aging。同时为使数据的单位根检验结果具有较好的稳健性,分别采用ADF检验法、PP检验法和KPSS检验法进行数据的平稳性检验。数据平稳性检验结果如表1所示。

表1 基尼系数和老龄化序列的单位根检验结果
注:“**”和“***”分别表示在5%、1%显著概率水平下显著。
由表1的检验结果可知,基于ADF检验时基尼系数序列(Gini)和人口老龄化序列(Aging)均是非平稳时间序列,其对应的检验统计值分别为-2.2705和-2.2930,均大于ADF检验10%所对应的临界值-2.6422和-2.6299,即接受序列包含单位根的原假设;而其差分序列的检验统计值分别为-3.1061和-2.4622,均小于ADF检验5%所对应的临界值-3.0124和-2.4622,即拒绝序列包含单位根的原假设。
基于PP检验时基尼系数序列(Gini)和人口老龄化序列(Aging)均是非平稳时间序列,其对应的检验统计值分别为-2.4080和2.2930,均大于PP检验10%所对应的临界值-2.6422和-2.6299,即接受序列包含单位根的原假设。而其差分序列的检验统计值分别为-6.7653和-3.8872,均小于PP检验1%所对应的临界值-3.7241,即拒绝序列包含单位根的原假设。同理,基于KPSS检验时,由于该检验方法的原假设与ADF检验和PP检验的原假设相反,但检验结果同样表明基尼系数序列和人口老龄化序列均为非平稳序列,而其一阶差分序列为平稳的时间序列。
结合上述分析,可以得到基尼系数序列和人口老龄化序列均为一阶单整序列,因此可以通过构建时变协整检验法捕捉二者之间是否具有时变的长期均衡关系,而不是仅仅存在一个或多个恒定的协整向量。
(二)时变协整模型的构建及检验
时变协整模型的构建主要是识别出收入不平等和人口老龄化之间是否存在结构断点,进而导致常系数的协整检验失效。通常情况下,进行断点识别使用最多的方法是Chow检验,但是该检验方法需要外生设定断点,断点的选择往往依据的是重大经济事件,这一约束使得断点独立于样本数据进而导致传统检验统计量失效。考虑到上述方法的缺点,参考Hansen (1992)[5]给出的一阶单整时间序列的回归模型参数是否具有时变性的检验方法。该方法与Chow检验最大的区别在于能够内生识别出结构断点,并且可以进一步判别协整方程的回归系数是否具有非稳定性。
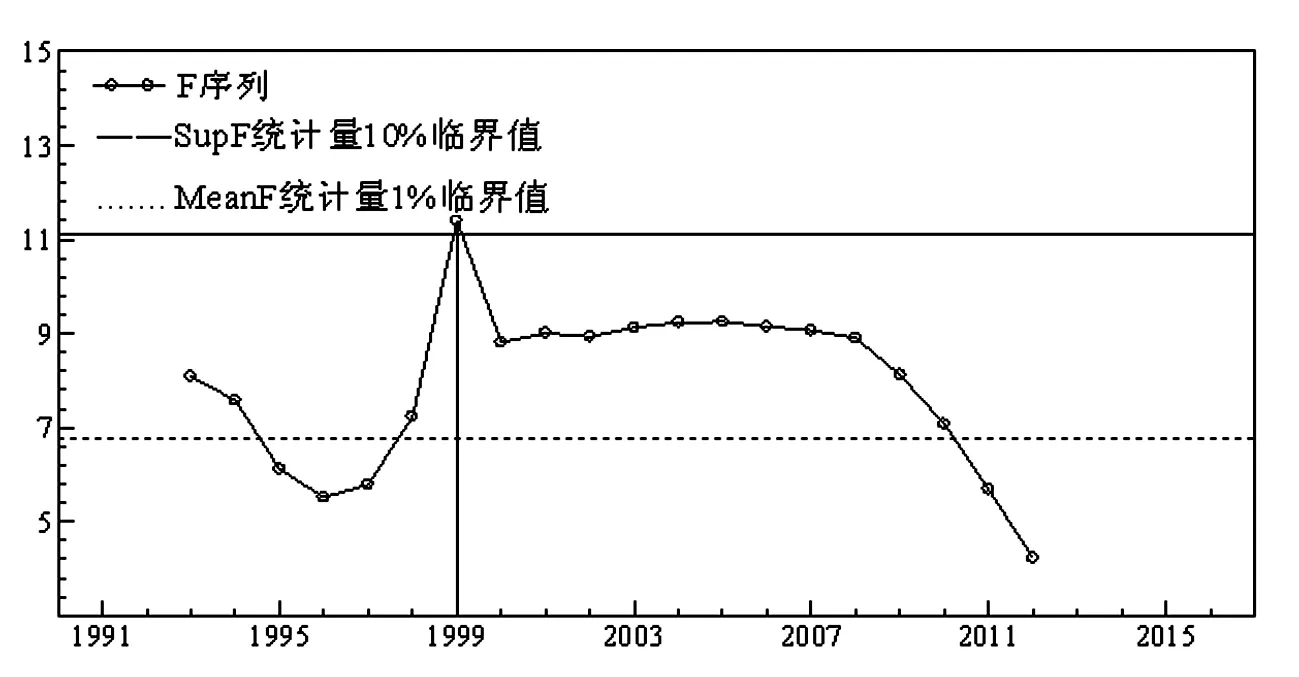
根据以上对基尼系数和人口老龄化原始数据进行平稳性检验的结果,确定二者均为一阶单整序列,可以通过构建带有变截距项的协整方程:
yt=αt+βtxt+εt
(1)
其中yt代表基尼系数序列,xt代表人口老龄化序列,αt和βt分别代表时变截距项和时变系数项。εt为服从白噪声过程的随机误差项。令Xt=(1,xt)′,Bt=(αt,βt)′,则式 (1) 可表示为:
(2)
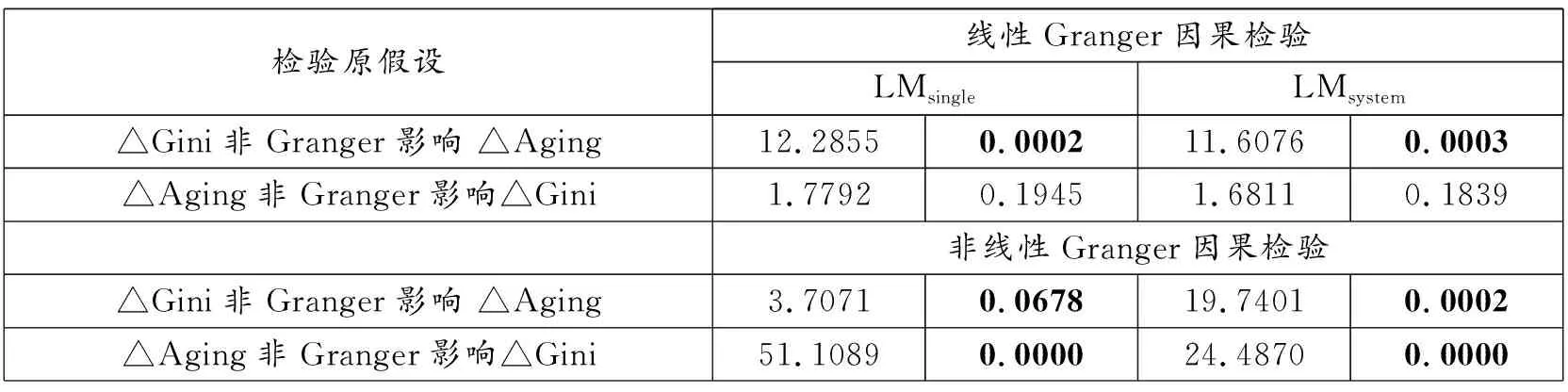
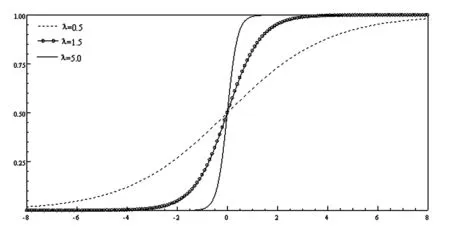
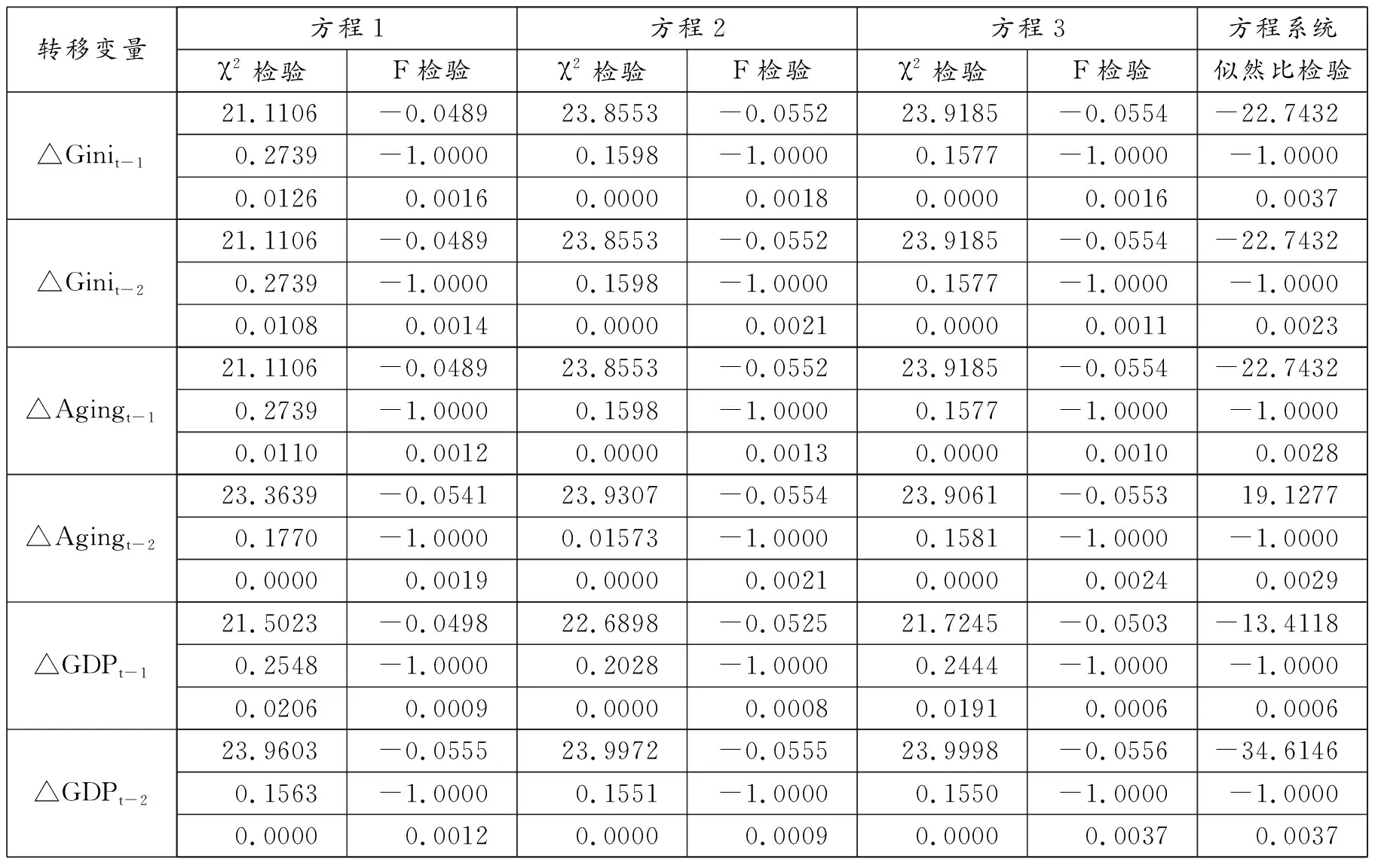
如果式(2)中的协整向量不存在变异,则时变系数向量Bt为以常数。否则,如果上述协整向量存在变异,可以通过设定如下假设对上述结构性断点进行检验。假设t时刻为内生结构断点(1 (3) 对于以上构建的检验协整方程是否具有时变特性的统计量,其中Fnt检验统计量的计算最为便捷,并且当样本容量较大时该检验统计量还有标准的渐进分布。但如果结构断点并不是外生时,即断点的选择和样本数据具有显著的相关关系,则Fnt检验统计量对应的检验功效便会极大下降,导致检验结果失准。有鉴于此,Hansen(1992)[5]给出了SupF和MeanF检验统计量,且二者能够克服上述缺陷;但出现的另一个问题是二者计算相对复杂,没有标准的渐进分布。Hansen(1992)[5]利用蒙特卡洛模拟方法给出了SupF和MeanF检验统计量1%、5%和10%显著水平的临界值,表2为基于SupF检验统计量和MeanF检验统计量的收入不平等和人口老龄化协整方程断点检验结果。 表2 基于协整方程的结构断点检验结果 注:SupF和MeanF检验统计量的1%、5%和10%的临界值均来自Hansen (1992)。 从表2的检验结果可以看出,无论是SupF检验统计量还是MeanF检验统计量均能在10%的显著水平下拒绝收入不平等和人口老龄化构成的协整方程中协整向量不存在结构断点的原假设;具体而言,SupF检验统计值(11.40)大于10%临界值(11.20),MeanF检验统计值(7.91)大于1%临界值(6.78)。这一检验结果充分表明,在研究的样本期间内,我国收入不平等和人口老龄化之间的长期均衡关系已经发生了明显的结构变化。 为了准确识别出结构断点的具体时点位置,我们绘制了基于已知结构断点的F检验统计量的时序图,如图3所示。从图3可以看出,基于已知结构断点的F检验统计量在1999年取得了最大值(对应为11.40),这表明1999年前后我国收入不平等和人口老龄化之间的长期均衡关系发生了显著的突变;而在1999年前后,对应的F序列均低于10%显著水平的临界值,进一步表明在统计学角度上,1999年我国收入不平等和人口老龄化之间的长期均衡机制发生了变异。 图3基尼系数与人口老龄化时变协整检验 我国收入不平等和人口老龄化之间的长期均衡关系在1999年发生了显著突变的这一结果可以从原始数据中找到解释。基于图1和图2中所绘制的原始数据时序图,我们可以清晰地观察到,1999年之前我国收入不平等呈现波幅大、增速快的特点,而在1999年后则表现出缓慢上升、波幅减小的新特征;与之对应的人口老龄化数据则在断点前表现出增速较缓的特点,而在断点后呈现出增速加快且无丝毫下降趋势的新特征。 当前全球几乎所有的国家都面临人口老龄化问题,只是程度不同而已。发达国家已经进入老龄化社会,发展中国家也正在迈入老龄化社会。相较于历史上大部分时期的人口结构,当下我国人民生活水平大幅提高、社会保障制度不断完善、医疗技术创新日新月异等因素带来了人口平均预期寿命的增加,我国正在进入持续40年的高速老龄化时期。出现老龄化这一新的人口现象,势必会影响收入不平等和人口结构的长期均衡关系,表现出显著的时变特征。 通常的情况下,检验变量之间的因果关系多数基于线性Granger因果检验方法。但当变量之间存在时变的协整关系时,或者说变量之间的长期均衡在某一时点发生了显著变化,则基于线性Granger因果检验方法得到的检验结果往往会缺乏准确性。结合前面的分析,我们知道我国收入不平等和人口老龄化之间存在时变的协整关系,因此,需要采用Péguin-Feissolle等(2008)[6]非线性Granger因果检验法来识别出二者之间的非线性传导机制。 令△Gini和△Aging分别表示收入不平等的差分序列和人口老龄化的差分序列,且二者均为弱平稳且遍历的时间序列,则有二者构成的二元随机系统可以是: △Ginit=fG(△Ginit-1,△Ginit-2,…,△Ginit-p,△Agingt-1,△Agingt-2,…,△Agingt-p;φG)+εGt 安徽六国化工是我国最早的磷酸二铵生产企业,多年来,在磷资源高效利用上积累了丰富的技术和经验。铜陵化学工业集团党委书记、董事长陈嘉生介绍:“作为与长江一路之隔的沿江企业,六国化工十分重视环境保护,不断加大资金投入,环境整治成绩显著,实现了‘三废’达标排放,磷石膏综合利用率达100%,在行业名列前茅。”他表示,平台启动后,六国化工将继续贯彻生态优先、绿色发展的战略决策,立足本业,结合现代农业发展需求,积极引进国际国内顶尖智力资源,不断提高磷资源利用率和技术、服务水平,为长江经济带区域绿色发展作出更大的贡献。 △Agingt=fA(△Ginit-1,△Ginit-2,…,△Ginit-p,△Agingt-1,△Agingt-2,…,△Agingt-p;φA)+εAt (4) 基于二阶泰勒近似和在二阶泰勒近似基础上提取主成分的刻画△Ginit和△Agingt短期交互影响的动态关系,均可采用单方程和方程系统的估计方法,构建拉格朗日乘子形式的约束检验统计量进行Granger因果关系检验。单方程和方程系统的拉格朗日乘子检验统计量分别为: (5) 和 (6) 式(5)和式(6)分别表示基于单方程和方程系统估计方法得到的非线性Granger因果关系检验拉格朗日乘子检验统计量。其中RSS1和RSS0分别表示参数约束检验中无约束回归和约束回归的残差平方和,U1和U0分别为系统方程无约束和约束回归对应的T×2维的残差矩阵。T表示样本观测值的个数,m为系统中方程的个数,tr(·)表示矩阵的迹。LMnonline-single和LMnonline-system检验统计量均服从F分布。 基于上述关于非线性Granger因果关系检验方法,通过对单方程的拉格朗日乘子检验统计值和方程系统的拉格朗日乘子检验统计值的计算,我们得到收入不平等和人口老龄化之间的短期交互影响关系的检验结果,如表3所示。此外,为充分捕捉到二者之间存在的非线性作用机制,我们同时采用了线性Granger因果检验方法和非线性Granger因果检验方法进行实证研究。 表3 变量间Granger因果检验结果 注:LMsingle和LMsystem分别基于单方程和方程系统构造的检验统计量,其中每一个统计量对应的第一列为统计量检验值,第二列为显著性概率,表中加粗字体表示均在10%显著概率下显著。 从表3的Granger因果检验结果中可以清楚地看到,当采用线性Granger因果关系检验方法时,得到的仅仅是存在收入不平等单向影响人口老龄化的结论。而当采用非线性Granger因果关系检验时,则检验结果表明收入不平等和人口老龄化在研究的样本区间内是互为因果关系的。 基于非线性Granger因果检验方法得到的结论更合理地捕捉到我国人口老龄化会影响收入不平等,而仅仅采用线性Granger因果检验方法则未发现上述现象。这同时也表明人口老龄化作用于收入不平等存在非线性的传导机制,而不是简单地意味着人口结构不同程度的改变均能带来同等程度的收入不平等。 对于收入不平等会影响到老龄化这一检验结果,可以从我国少儿抚养比占总人口的比重的角度进一步理解。自20世纪90年代以来,我国少儿抚养比占总人口的比重持续下降,直到2010年左右才基本维持在近17%左右。[注]数据来源于WIND统计数据库。其原因可能是由于收入不平等导致多数人抚养幼儿的成本负担增加。人口老龄化既有来自于人口预期寿命增加引起的顶部老龄化,又有来自于生育率下降造成的底部老龄化[3];而底部老龄化问题同样不容忽视。 基于前面的计量模型,对应的检验结果表明收入不平等和老龄化之间存在显著的非线性协整关系和非线性Granger因果关系。此前的计量模型主要是检验二者在方程构建方面是否存在时变系数,但并未能形象地观测出变量间随时间的递进会表现出何种形式。为此,考虑到脉冲曲线分析法可以更直观地观测所考察的经济变量间的动态影响路径,本文通过构建平滑迁移向量自回归模型 (STVAR) 分析收入不平等和老龄化间的动态影响效果。 自Sims (1980)[7]提出向量自回归模型后,该模型在分析研究复杂的经济问题上发挥了至关重要的作用。但随着时间的推移,计量经济学家发现现实中的经济变量之间并不与线性向量自回归模型中的假设一致;换言之,现实经济变量存在更复杂的传导机制,并非是简单的线性关系。考虑到上述线性向量自回归模型的局限,参考Weise (1999)[8]构建的逻辑平滑向量自回归模型 (LSTVAR),分析收入不平等和老龄化之间的短期动态非线性传导机制。 包含基尼系数一阶差分序列、人口老龄化一阶差分序列和实际产出同比增速序列作为内生变量的p阶滞后向量自回归模型可以表示为: (7) 其中,Xt=(x1t,x2t,x3t)′,x1t,x2t和x3t分别代表基尼系数一阶差分序列、老龄化一阶差分序列和实际产出同比增速序列。Γ0=(γ10,γ20,γ30)′为常数项对应的系数列向量;Γi=(γi1,γi2,γi3)′,γij=(γij,1,γij,2,γij,3)′为第j个方程i阶滞后内生变量(Xt-i) 对应的回归系数向量;μt为随机误差列向量。由于内生变量可能存在非线性数据生产机制,可以将式 (7) 表示的线性向量自回归模型拓展为非线性平滑迁移向量自回归模型的形式,其中非线性平滑向量自回归模型中第j个方程可表示为: (8) 其中,φ0j对应的是非线性部分中常数项的回归系数,φij为非线性部分中内生变量对应的回归系数列向量。Fj(·)表示转移函数,具体分为逻辑型转移函数和指数型转移函数,其中逻辑型转移函数形式为: F(zt;λ,c)={1+exp[-λ(zt-c)]}-1-1/2 (9) 其中,zt表示转移变量,可以为内生变量滞后项、外生变量和内生变量的函数;λ和c分别表示转移斜率和位置参数,转移斜率越大,表示经济变量在不同区制的转移速度越快,反之则反;特别地,当转移斜率趋于无穷时,则转移函数在位置参数附近表现为跳跃式的门槛模型,当转移斜率趋于零时,则转移函数值也同样趋于零,此时的非线性模型退化为线性向量自回归模型。绘制不同转移斜率下转移函数图像如图4所示。为简单起见,将位置参数设置为0。换言之,线性向量自回归模型和门槛向量自回归模型是平滑迁移向量自回归模型的特例。 图4不同转移斜率对应的转移函数图像 从图4中可以直观地观察到转移斜率的变化对转移函数图像的影响,当转移斜率逐渐增大时,其对应的转移函数在位置参数附近的转变速度也变大。具体地,当转移斜率为0.5时,转移函数的函数值在0至1之间的变化速度最慢,当转移斜率增大到5时,转移函数对应的函数值由0迅速变化到1。 对于平滑迁移向量自回归模型的线性检验,由上面的分析可知,到转移斜率λ=0时转移函数对应的函数值为0,此时平滑迁移向量自回归模型退化为线性的向量自回归模型,故可以将原假设设定为H0:λ=0,当原假设成立时,对应的模型为线性向量自回归,变量间具有线性关系;否则,拒绝原假设表示变量间具有非线性关系。我们注意到,当原假设成立时,式(8)中包含冗余的参数(即转移斜率参数和位置参数在原假设成立的条件下是不可识别的),此时传统的参数约束检验统计量没有渐进的统计分别,故检验方法失效。 参考Weise(1999)[8]的做法,将式 (8) 在λ=0处进行泰勒展开,得到线性检验的辅助回归方程: (10) (11) F分布类型的检验统计量: (12) LR=T(log|Ω0|-log|Ω1|)~χ2[3m(mp+1)] (13) 式 (13) 中,Ω0和Ω1分别表示平滑迁移向量自回归模型对应的辅助回归方程的约束和无约束方差协方差矩阵。结合上述基于单方程的线性检验和基于方程系统的线性检验方法,包含测度收入不平等、人口老龄化和实际产出的三元平滑迁移向量自回归模型的线性检验结果如表4所示。 表4 STVAR模型线性检验结果 注:方程1、方程2和方程3分别代表收入不平等方程、老龄化方程和实际产出方程;对于每一个转移变量,第一行为检验统计量,第二行为依据渐进分布计算的显著概率,第三行为利用自举法 (bootstrap) 模拟的显著性概率,抽样次数设定为10 000次。 由表4的模型线性检验结果可以看出,当老龄化一阶差分滞后项和二阶差分滞后项分别作为转移变量时,无论是基于单方程检验还是方程系统检验,抑或是基于卡方检验统计量和F检验统计量,方程1、方程2和方程3均在1%显著概率下拒绝模型为线性的原假设,即方程中所包含的经济变量间存在显著的非线性关联机制。 此外,由表4还可以看到,当转移变量为基尼系数一阶滞后和二阶滞后、实际产出同比增速的一阶滞后或者二阶滞后时,模型同样表现出非线性的特征。由于是基于老龄化对收入不平等的影响视角来分析变量间的短期动态影响机制,因此选择老龄化作为转移变量,并依据老龄化的不同程度将研究样本分为老龄化高区制和老龄化低区制,进一步研究其对收入不平等是否具有显著的非对称影响,或者不同的影响程度。同时考虑到样本数据是年度数据且样本容量较少,故选择老龄化一阶差分滞后项作为转移变量。后面的脉冲曲线分析同样也将转移变量设定为老龄化一阶差分滞后项,不再赘述。 基于平滑迁移向量自回归模型计算的脉冲响应曲线与线性向量自回归模型的脉冲曲线不同,对于线性模型而言,模型中的回归系数在整个样本区间为固定数值,而在非线性模型中,解释变量前的回归系数是非恒定在,如在不同的样本区制内,同一解释变量前的回归系数大小不同或者符号迥异。此时采用线性模型计算脉冲相应曲线有失偏颇,因此本文参考Koop (1996)[9]提出的计算非线性向量自回归模型脉冲曲线的方法,通过计算估计出转移函数中的转移斜率和位置参数,可以进一步计算出在位置参数两侧的脉冲曲线函数。 人口老龄化是我国经济社会发展中必须直面的现实问题。从各国人口老龄化的历史进程上看,人口年龄结构逐渐老化会给一个国家或地区的经济社会发展带来一系列消极的影响。与此同时,收入不平等会影响经济发展的驱动力,并引发诸多社会问题,影响经济发展和社会稳定。我国已经进入老龄化社会,政府在制定政策改善收入不平等的同时,应该注意人口结构的改变对收入不平等所产生的影响,加快完善我国老年人口的社会保障体系。
四、我国收入不平等与老龄化的因果关系检验
五、我国收入不平等与老龄化的脉冲响应分析
(一) 平滑迁移向量自回归模型 (STVAR) 的构建
(二)非线性检验
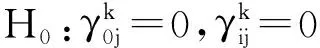
(三) 变量间脉冲响应分析
六、结论和政策建议

