一种改善BLDCM调速性能的模糊矢量控制策略*
朱明祥,孙红艳,慈文彦,窦爱玉,袁丽丽
(南京师范大学泰州学院 电力工程学院,江苏 泰州 225300)
0 引 言
永磁BLDCM因其结构简单、运行可靠、功率因数高、调速性能和机械特性好等特点,被广泛应用于国防、航空航天、医疗器械、家用电器等各个领域[1]。由于BLDCM是以自控式运行,所以重载启动时无需另加启动绕组,同时负载突变时不会出现振荡和失步等问题。理想的永磁BLDCM反电势为120°平顶的梯形波,通以方波电流时可产生恒定转矩。由于电机设计或制造的原因,实际的BLDCM反电势波形不是理性的梯形波,也不是正弦波,其转矩系数随转子位置角的变化而改变,通以方波电流时会产生低频转矩脉动;此外,BLDCM一般采用两相导通模式进行控制,换相时由于电流上升率和下降率不等,存在换相转矩脉动[2]。矢量控制方式将电流分解成平行和垂直于转子磁场的两个电流分量,所以对电流地控制可以等效为直流,使电机在低速运转和高速时一样地平滑,因此文中采用矢量控制方式进行调速控制,增强电机调速控制中的整体性能。
针对永磁BLDCM高性能要求地控制,国内外学者提出了诸多控制方案及改进措施。文献[3-5]提出改进型直接转矩控制策略,较好地抑制了转矩脉动且电机动态调节性能得到很好地改善,但电流稳定性不够理想。文献[6]提出了改进型无位置传感器控制策略,该策略引入光滑的双曲正切滑模观测器来减少系统抖动,但电流在换相时存在脉动现象,进而发生转矩脉动。文献[7-8]提出采用滞环电流跟踪型PWM逆变器控制策略实现电流控制,使系统具有较好的动静态特性,但在电流换相时,电流及转矩均有一定程度的脉动现象。文献[9-12]提出采用矢量控制策略,使系统电流与转矩脉动更小,并提高电源利用效率,但其相对于方波控制,存在系统算法复杂的问题。
鉴于此,在分析BLDCM调速控制算法上,考虑到矢量控制的特点,提出一种基于模糊控制的BLDCM矢量控制调速策略。该策略使用模糊方式动态调节参数,进而增强BLDCM调速性能;使用矢量控制抑制电流及转矩脉动,使转速调节更平滑。经MATLAB仿真模拟出该策略的运行状态,并细致分析了BLDCM的运行中各参数地变化,验证了该方法的正确性与有效性。
1 无刷直流电机数学模型
永磁BLDCM转子进行特殊地磁路设计,可获得梯形波的气隙磁场。为了分析的方便,研究首先对BLDCM模型作以下假设:忽略空间谐波,定子三相绕组完全对称,空间互差120°,参数相同;忽略定子铁心齿槽效应地影响;忽略功率器件导通和关断时间地影响,功率器件的导通压降恒定,关断后等效无穷大;忽略定子绕组电枢反应地影响,各绕组自感和互感恒定不变;电机气隙磁导均匀,忽略磁路饱和,不急磁滞损耗与涡流损耗。上述假设下三相定子变量数学模型为[13-14]:
(1)
式中p为微分算子;ua,ub,uc为定子三相绕组电压;ia,ib,ic为三相绕组电流;ea,eb,ec为三相绕组反电势;R为三相绕组电阻;LS为定子绕组自感;LM为定子两相绕组互感。
当电机采用三相星型绕组时,有ia+ib+ic=0,并且令L=LS-LM。将其代入式(1),整理得:
(2)
永磁BLDCM的电磁转矩方程可表示为:
(3)
式中Ω为BLDCM的机械角速度(rad/s)。
(4)
(5)
式(4)中ψ(θ)为A相绕组的永磁磁链;θ为转子位置角,如图1(a)所示;式(5)中φ(θ)为A相绕组磁通;N为A相绕组匝数;S为绕组在定子内径表面围成的面积;B(x)为沿x轴承梯形分布的转子永磁体径向气隙磁密,B(x)周期为2π,同时满足B(x+π)=-B(x)。结合式(4)、式(5)可得:
ea=ωrψmfa(θ)
(6)
式中ωr为转子角速度;ψm=2NSBm,为A相绕组磁链幅值;fa(x)=B(x+π/2)为A相幅值为1的单位反电势。
假设电机气隙磁场为标准的梯形波,平顶宽度为120°,则磁密分布B(x)的具体数学模型为:
(7)
式中Bm为B(x)磁通分布中120°平顶对应的磁通幅值,A相绕组磁通如图1(b)所示。


图1 A相绕组位置及磁通分布
同理可得,B相与C相的反电势数学模型为:
(8)
(9)
根据Clark和Park变换及其逆变换,可将三相静止坐标系下定子电压变量转换成同步旋转坐标系下的d、q电压分量为:
(10)
d-q坐标系下转矩公式为:
(11)
上式即为BLDCM在矢量控制下的转矩公式,比常规的永磁同步电机矢量控制的转矩公式更加复杂。在矢量控制系统中,若采用id=0的控制方式,上式可化简为:
(12)
从式(12)可看出,当电机运行在稳态状态下,电磁转矩近似恒定,但依旧会随着时间做周期性地变化。
2 模糊控制的矢量控制策略
2.1 BLDCM控制策略
BLDCM调速策略可以使用方波控制、弦波控制以及矢量控制等。使用方波控制可以更便捷地对电机进行控制,且具有更高的转速,但转矩脉动和噪声较大。而弦波控制相对于方波控制,在复杂度上要高于前者,且最大运行转速受PWM频率地限制,但其转矩脉动噪声较小。弦波式控制能得到方波控制所不能达到地平滑控制,然而这种理想的控制方式只能对电机低速运动起到较好地平滑作用,而对于电机的高速运动则没有任何作用,因为当电机转速不断提高,PI控制器超出极限工作带宽时,此控制方式将失效。矢量控制将电流分解成平行和垂直于转子磁场的两个电流分量,所以对电流地控制可以等效为直流,使电机在低速运转和高速时一样地平滑。
传统矢量控制方式多采用PI控制器,该种控制方式是靠目标与实际之间的误差来决定消除此误差的控制策略,而不是靠对象的输入-输出关系,只要参数整定合适,就能使系统达到指标,但该控制策略已不能满足当前BLDCM控制的高要求,因此提出采用模糊方法的矢量控制策略,使用模糊方法对系统控制器参数进行动态调整,以适应系统高性能地要求。
此策略的系统控制框图如图2所示。系统中使用模糊控制器代替转速环PI控制器,再将指令值经过电流环、矢量坐标变换以及空间矢量脉宽调制(SVPWM),最后通过逆变器对BLDCM进行高性能驱动控制。

图2 模糊控制的BLDCM矢量控制系统框图
2.2 模糊控制器设计
模糊控制器结构如图3所示。在模糊控制器地设计过程中,由于操作者经验难以描述,控制对象过程及其参数复杂多变,故使用模糊控制方法来解决这一难题。

图3 模糊自适应PI控制器结构框图
2.2.1 隶属度函数与模糊逻辑决策地确立
转速误差e、误差变化率ec的隶属度函数曲线如图4所示,输出量Δkp、Δki的隶属度函数曲线如图5所示。将电机转速的实测值与给定值的误差e和误差变化ec作为输入变量,令其量化等级为3级,即{-1,0,1},两者均服从Z型、三角型以及Sigmoid型隶属度函数分布曲线。以Δkp、Δki作为输出变量,量化等级为3级,即{-1,0,1},两者均服从Z型、三角型以及Sigmoid型隶属度函数分布曲线,各输入输出的模糊子集均为{N,Z,P}[15]。

图4 e和ec的隶属度函数图

图5 Δkp和Δki的隶属度函数图
模糊逻辑决策采用Mamdani算法的max-min进行合成,取误差e和误差变化率ec的模糊集进行直积运算,其结果再和模糊算子进行模糊矢量积运算得出系统的控制输出量。
2.2.2 控制规则的确立
Δkp整定的模糊规则表如表1所示,Δki整定的模糊规则表如表2所示。当响应上升时,需要增加kp,以加快动态响应过程,但当响应出现超调时,需要减小kp,以增大系统阻尼,使响应快速进入稳态;当转速误差较大时,ki可以取为0,随着误差的减小,ki将逐渐增大以消除系统静差。参数整定时,必须综合考虑两个参数的影响以及联系,利用所设立的模糊规则进行模糊推理,并查询模糊矩阵表进行参数调整[16-17]。

表1 Δkp的模糊规则表

表2 Δki的模糊规则表
2.2.3 模糊量反模糊化
文中反模糊化采用输出更加平滑的重心法,其表达式为[18]:
(13)
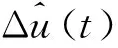
3 BLDCM控制系统Matlab/Simulink仿真分析
在MATLAB环境下,采用Simulink和Simscape的块图模型建立永磁BLDCM控制系统的仿真模型。采用基于模糊控制的BLDCM矢量控制策略,电机和实验的参数见表3。

表3 无刷直流电机模型和实验参数
此实验的主要目的是将所提出的模糊矢量控制策略与方波控制策略进行对比,来验证此策略的优越性。
此实验中,两个策略都进行了0.1 s地仿真。在t=0 s时,给定负载转矩为0 N·m,即让电机空载启动运行,给定转速为800 r/min,在t=0.05 s时,加上负载5 N·m。基于模糊控制的BLDCM矢量控制策略输出转矩波形如图6(a)所示,方波控制的BLDCM调速策略输出转矩波形如图6(b)所示。通过对比两者输出转矩波形可知,前者在输出转矩稳定时,转矩脉动更小,在t=0.05 s加载后,电机输出转矩也比后者稳定且脉动较小。后者整体的输出转矩脉动幅值都大于前者,但前者在0.02s前,转矩峰值上存在一个大范围地突变。

图6 输出转矩波形
基于模糊控制的BLDCM矢量控制策略电流波形如图7(a)所示,方波控制的BLDCM调速策略电流波形如图7(b)所示。通过对比两者电流波形可知,前者无论是在加载前还是加载后,电流稳定性都优于后者,但前者的最大电流比后者大。

图7 电流波形
基于模糊控制的BLDCM矢量控制策略反电势波形如图8(a)所示,方波控制的BLDCM调速策略反电势波形如图8(b)所示。通过对比两幅图可知,前者的反电势比后者更加稳定,由于反电势与转速成正比,因而反电势的不稳定对转速会产生一定影响。
基于模糊控制的BLDCM矢量控制策略转速波形如图9(a)所示,方波控制的BLDCM调速策略转速波形如图9(b)所示。前者在tr=2.52×10-3s时达到给定转速,并在tp=2.74×10-3s时到达峰值转速,其超调量为σ%=1.375%,在t=0.05 s时加载,此时产生ΔCmax=10 rpm的动态速降。后者在tr=4.62×10-3s时达到给定转速,在t=0.05 s时加载,产生ΔCmax=190 rpm的动态速降。对比两者可知,前者的上升时间优于后者,且在加载后产生的动态速降与转速稳定性也优于后者。


图8 反电势波形

图9 转速波形
4 结束语
针对无刷直流电机转矩脉动大、电流畸变程度大以及反电势不稳定造成转速波动等问题,给出了一种基于模糊控制的BLDCM矢量控制调速策略。实验结果表明,采用该策略,其输出转矩具有更小地脉动以及更好的稳定性;电流的畸变程度与稳定性在加载前后都得到较大改善;电机的反电势与转速相对于方波控制方式,具有更稳定更平滑等优势,且该调速策略的动态性能也更优,进而使系统整体性能得到较大地提升,仿真结果证明了其正确性与有效性。

