转向机动拖曳线列阵空间谱稀疏重构*

袁 骏，蔡志明，肖 卉，奚 畅

（1.海军工程大学电子工程学院，武汉 430033；2.空军预警学院，武汉 430019）

0 引言

拖曳线列阵声纳凭借其工作频率低、阵列增益高、平台干扰小等优势，已成为水下低频、远距离探测的有效技术手段[1]。常规的拖线阵由多个全向水听器按照一定的间距线性排列而成。由于沿阵列左右对称的目标信号到达阵列的时间差完全一致，所以单纯依赖常规拖线阵直接探测的结果往往难以决定目标的真实角度位置，这种现象常被称为“目标左右舷模糊”。解决左右舷模糊的最简便方法是利用拖曳平台的转向机动，人工分析转向前后目标角度的变化趋势，最终完成目标左右舷分辨。然而在转向过程中，阵形容易发生畸变，从而导致测向误差恶化，影响目标的稳定跟踪。为了更加有效地解决左右舷模糊问题，研究人员对拖线阵接收信号的形制进行改进，提出了采用双线阵、三元组水听器阵以及矢量水听器阵[2-4]等多种方法。但是受到制造工艺、生产成本以及平台适装性等条件的限制，这些新体制拖线阵在军事、民用领域还未被广泛使用。因此，采用信号处理方法实现拖线阵的全向空间谱估计一直是研究的热点。

在拖线阵的转向机动过程中，阵形的畸变从根本上破坏了目标左右舷对称的条件，在已知阵形的情况下，原理上可以抑制拖线阵的左右舷模糊[5]。但是，阵形畸变同时也会减小目标信号的接收增益，并且每个处理节拍内的有效快拍数大幅减少限制了大部分自适应波束形成算法的应用。为了实现拖线阵声纳全向有效的目标探测，本文将压缩感知理论应用到拖线阵的空间谱估计问题，提出了基于多个波束域快拍的机动拖线阵空间谱稀疏重构模型，并采用前向后向分裂算子法进行优化求解。与常规波束形成方法相比，本文方法提高了左右舷模糊抑制能力，改善了目标方位估计性能，对实现拖线阵声纳全向实时空间谱估计具有重要的现实意义。

1 机动拖线阵接收信号模型

1.1 转向机动阵形模型

采用流体力学领域的“Water Pulley”模型[6-7]对转向机动下的拖线阵阵形进行数学建模。假设拖线阵的M个阵元沿阵列均匀布放，阵元间距为d，阵首第1个阵元位于直角坐标系原点。根据“Water Pulley”模型，拖线阵在进行小角度转向过程中，可以认为当前阵元的运动轨迹与前一个阵元的轨迹是近似吻合的。

假设在时刻t，第1个阵元的即时航向角记为h（t），若每隔△T时刻可以得到一次艏阵元航向角，则在时间T内，共有个航向角信息，记为 h（t）=[h（t），h（t-△T ），…，h（t-（L-1）△T ）]T。因此，拖线阵转向时的航向角向量可以用一阶AR动态模型描述为

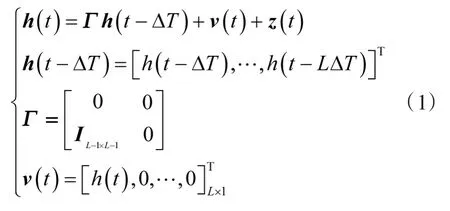
式中，v（t）是模型更新的驱动项，主要由第1个阵元的即时航向角决定，在工程中，该信息可以通过阵内罗经测量得到；z（t）表示测量航向角受到实际环境的扰动，满足独立同高斯分布假设。

假设拖船航速恒定为V m/s，L个航向角可以看成是对拖线阵阵形的 L 次采样，第 l∈{2，3，…，L}个航向角对应的坐标向量可以表示为

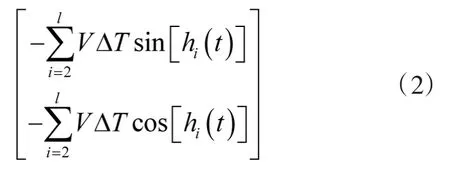
由于实际的转向拖线阵阵形可以合理地用抛物形方程y=Ax2+Bx+C来近似，采用最小二乘拟合方法可以对方程的系数进行求解，从而可以得到转向拖线阵阵形的抛物线模型。

假设拖线阵在拖曳过程中不发生拉伸形变，其总长度保持不变，所以第m个阵元的横坐标xm可以通过下式计算得到

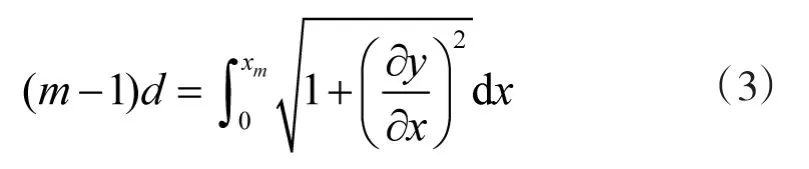
1.2 拖线阵接收信号稀疏模型

考虑由各向同性水听器阵元组成的拖线阵接收远场平面波信号，信号源与阵列位于同一个水平坐标系内，如图1所示。

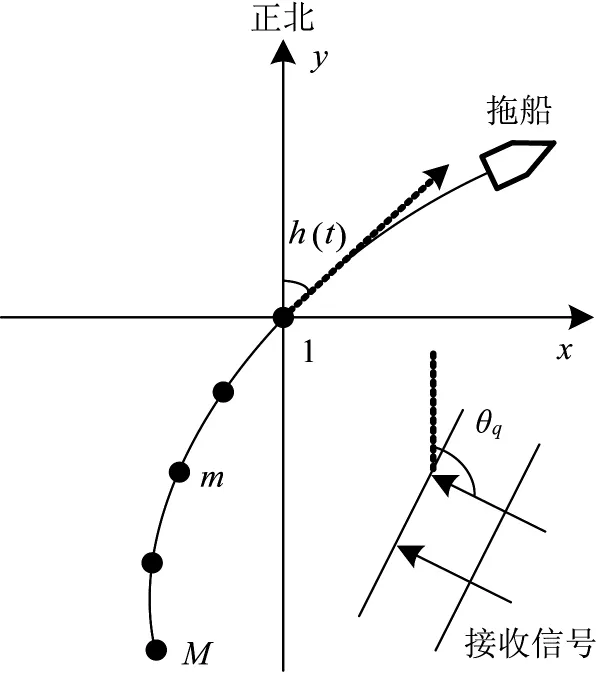
图1 机动拖线阵坐标系

不失一般性地假设阵列在第三象限，在时刻t，拖线阵的第m∈{2，3，…，M}个阵元的坐标位置向量可以表示为

第q个信号的单位方向向量表示为

则从 θq∈[0°，360°）方向入射信号的阵列响应向量为

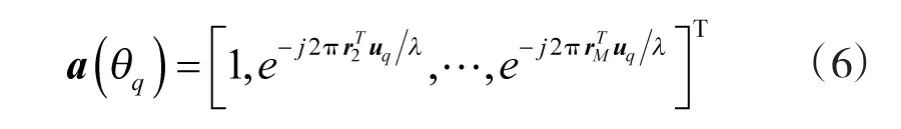
根据稀疏重构理论[8-10]，假设空间真实存在P个信号，将感兴趣的信号角度空间Θ划分成Q个角度分量，P＜＜Q，对空间信号的采样可以用阵列响应矩阵表示为

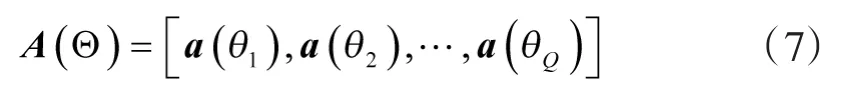
式中，θ1，θ2，…，θQ为离散化的测量方位角。

因此，阵列接收信号的稀疏模型表示为

式中，y∈CM是基阵对Q个方向采样的复包络向量，x∈CQ是所有Q个离散方位角上的窄带信号复包络向量，且信号间互不相关，n∈CM是阵元接收的各向同性噪声复包络向量，是满足独立同分布的零均值复高斯随机过程，且与信号不相关。

2 算法描述

主要思想：在拖线阵转向机动过程中，远场目标真实方位在多个连续波束快拍中的变化可以忽略不计，而模糊目标的方位随着阵列转向发生快速的变化。因此，可以对多个波束快拍的总体重构误差进行约束来估计空间谱。

首先，给出基于波束域快拍的拖线阵空间谱稀疏表示模型[8]。由于拖线阵的阵形是一维线性的，所以对不同方向形成波束时，主瓣宽度会随着扫描角度偏离正横方向而逐渐展宽。因此，在设计拖线阵预成波束指向角时，最终得到的预成多波束角度分布是非线性的。假设在360°空间范围内共形成K个波束，波束指向角为 φk∈[0°，360°），（k=1，…，K），常规波束形成的输出信号功率为

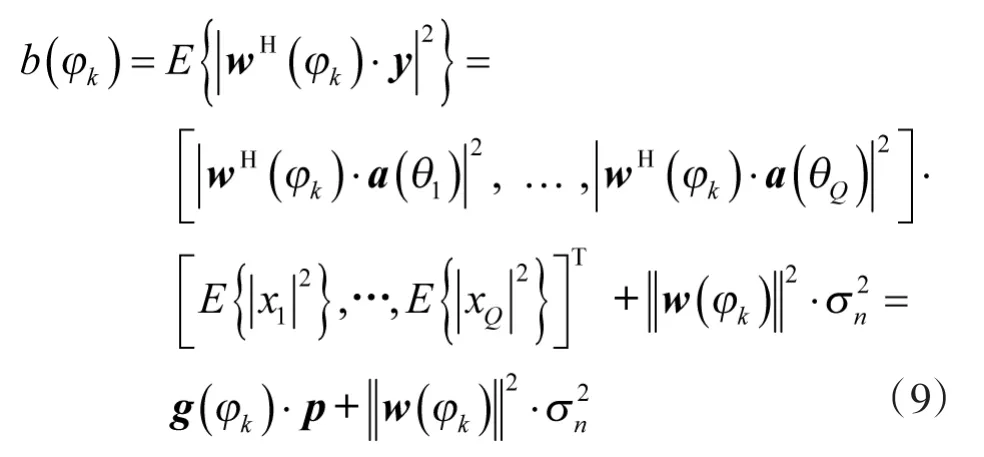
因此，基于波束域快拍的拖线阵空间谱稀疏模型为

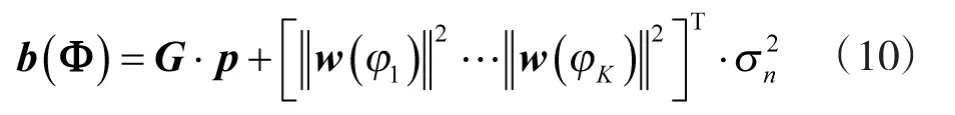
由于空间角度划分数Q＞K，且P＜＜Q，根据压缩感知理论，该欠定问题可以通过引入l1-范数正则条件进行凸优化求解。

在此基础上，利用拖线阵转向机动过程中的目标方位变化固有特征，同时考虑转向过程中多个时刻的波束域快拍，进行多时刻联合空间谱稀疏重构，势必能抑制左右舷模糊，从而改善探测效果。因此，在已知拖线阵阵形的条件下，机动拖线阵联合空间谱稀疏重构可以表述为如下变分问题[11-12]

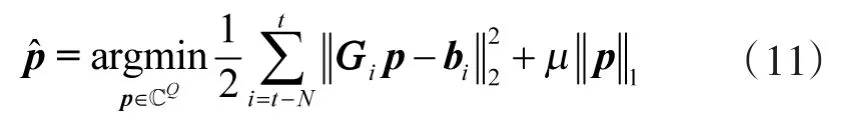
式中，N为波束快拍的数目，μ＞0是一个常数。

上述凸优化问题可以采用经典凸规划、活动集等算法进行求解，然而在大尺度空间角度精细划分情形下，这些算法的求解过程将十分耗时，因此，需要更加行之有效的算法。前后向算子分裂[13-14]是凸优化分析中一种快速、有效的算法，它将待优化函数f（x）看成是两个凸函数的和f（x）=f1（x）+f2（x），采用迭代求解的方式，分别对f1（x）的前向步（梯度下降）和f2（x）的后向步（临近算子）进行计算，固定点迭代公式为

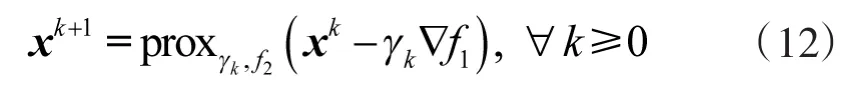
式中，k 为迭代的次数，γk＞0 为步长，f1表示函数的梯度，表示函数的临近算子，定义为

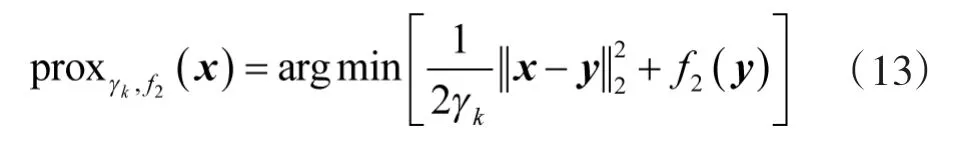
由于待优化函数f（x）是凸的，并且f1（x）具有可微的β-Lipschitz连续梯度，从而可以保证算法是收敛的。通过上述分析，针对式（11），基于前后向算子分裂的固定点迭代公式如下

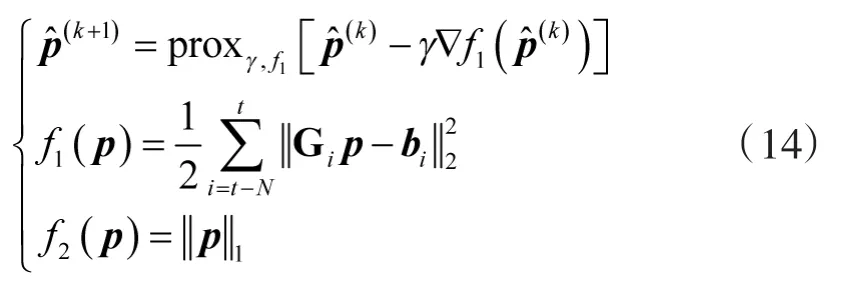
经过化简，最终的迭代计算式为

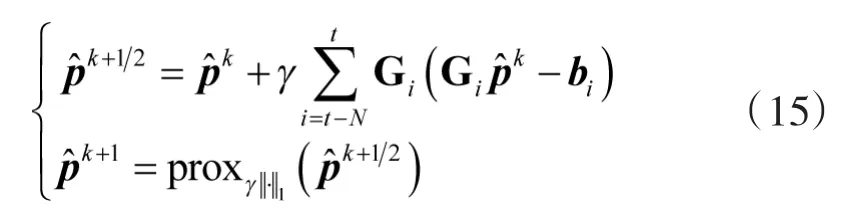
3 性能分析

3.1 计算机仿真

首先通过计算机仿真验证本文方法的有效性。仿真中采用的拖线阵是由各向同性水听器均匀排列而成的，阵元数M=70，阵元间距为2 m。拖船航速6 kn，向正北方向航行，在第0时刻开始以0.3°/s的转向速度向东转向至27°，各阵元航向的估计噪声方差为0.2°。假设空间存在两个中心频率为375 Hz的远场窄带信号源，方位分别为80°和120°，且强度相等；每个阵元接收的背景噪声符合独立同高斯分布。每次常规波束形成采用2个阵元域快拍，并假设在计算过程中，阵形保持不变。本文方法采用N=5个波束域快拍进行联合空间谱稀疏重构，空间角度被均匀划分为Q=360份。

图2给出了在拖线阵开始转向后第90 s时的空间谱估计性能仿真结果。图3给出了当信噪比为0 dB时，CBF方法和本文方法估计的空间谱图，图中“*”表示目标的真实角度位置。结果表明本文方法能够获得高分辨的空间谱，并且有效抑制了左右舷模糊。

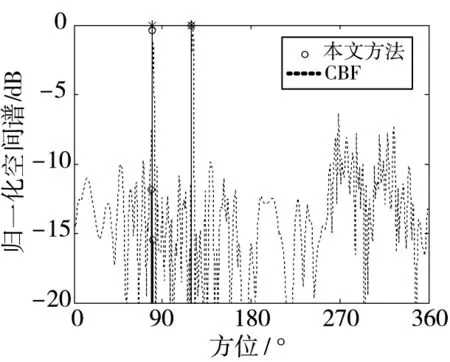
图2 估计的空间谱图

图3～图5给出了100次蒙特卡洛仿真的统计结果。图3为模糊抑制比[5]与信噪比的关系图，在目标信噪比大于-18 dB时，本文方法的模糊抑制能力远好于CBF方法。图4给出了检测概率与信噪比的关系，本文方法的检测性能提高了约4 dB。图5给出了方位估计均方误差与信噪比的关系，本文方法的误差随着信噪比增加下降更快，具有更好的测向精度。

3.2 海试数据处理结果

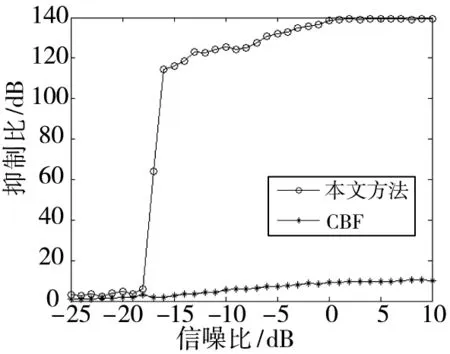
图3 模糊抑制比随信噪比的变化情况

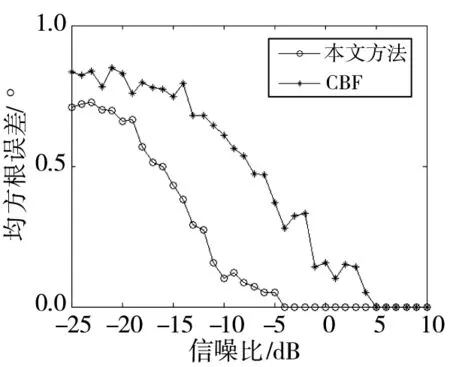
图5 目标方位估计均方根误差随信噪比的变化情况

采用2016年5月在我国南海海域进行的一次水声探测试验数据进行算法的可行性验证。试验时，试验拖船同时拖曳主动声源和被动线列阵，主动声源周期性地发射脉冲信号，同时试验海域存在水下不明周期性干扰。信号处理时，选取间隔为设计频率半波长的70个水听器数据进行空间谱估计。拖线阵初始航向约为51°，向正北方向转向，平均转向速度约为0.14°/s。

图6 阵形未校正的常规波束形成方位时间历程图

图6是CBF方法在拖线阵阵形保持线性假设下的方位时间历程图。可以看出每个目标在以航向（图中虚线表示）对称的角度上存在着模糊目标，拖线阵转向引起的阵形畸变影响了目标方位的估计精度。同时可以发现试验现场态势较为复杂，拖船周期发射主动脉冲影响了被动拖线阵的持续接收；目标2位于拖线阵尾部的端射方向附近，并在拖线阵转向过程中（约100 s～140 s间）穿越了阵尾，目标轨迹发生了分裂；目标1与目标3之间存在着周期性的水下不明干扰。

图7是采用估计阵形进行的CBF方位时间历程图。从图中可以发现，目标1的测向精度得到明显改善，其模糊目标在角度上发散，强度降低；目标2由于处在端射方向附近，其测向精度并未有改善；目标3在120 s以后逐渐进入阵尾端射范围，并与目标2的模糊目标重叠，测向精度受到影响。

图7 阵形校正后的常规波束形成方位时间历程图

图8是本文方法得到的方位时间历程图，与图7相比，目标1的模糊目标得到了进一步抑制；目标2在穿越阵尾前后的测向精度得到明显改善；由于目标3的强度较弱，在其进入阵尾端射区后探测效果并不明显。

图8 本文方法的方位时间历程图

4 结论

本文根据拖线阵转向机动时的目标方位变化特征，提出了基于多个波束域快拍的空间谱联合稀疏重构模型，并采用前后向算子分裂方法进行优化求解，从而有效提高了数值求解的效率。计算机仿真结果表明，本文方法在阵形已知的条件下，只需少量的波束域快拍就能有效抑制左右舷模糊，并在测向精度方面优于常规波束形成方法。最后，通过对海试数据的处理分析初步验证了本文方法的可行性。