有人机/无人机协同下空空导弹发射区仿真分析*

李英豪，樊 蓉，郭 创，王厚哲

（1.空军工程大学航空航天工程学院，西安 710038；2.西安铁一中滨河中学，西安 710038）

0 引言

现代空战正逐渐由以平台为中心向网络为中心过渡，有人机/无人机协同作战体系使空空导弹的发射和制导不再局限于同一平台，无人机通过选择合理策略前置飞行并发射导弹，极大改善了空空导弹的攻击条件和攻击范围。传统攻击区没有考虑无人机的飞行策略，也不涉及协同因素，因此，不再适用这一作战体系，需要进行改进。

目前，有人机/无人机的协同作战相关问题已经有一定研究成果，但是对于有人机/无人机协同条件下空空导弹的发射区研究比较少。文献[1]研究双机编队下的空空导弹协同发射区，考虑编队协同约束，并使用黄金分割法搜索导弹发射区，没有触及与无人机协同。文献[2]研究空空导弹弹射后的动态攻击区计算以及信息提示，与无人机前置飞行攻击有诸多相似之处。文献[3]研究网络瞄准下空空导弹允许发射区。同时，无人机的飞行策略与攻击轨迹是有人机/无人机协同发射区的关键因素，目前攻击轨迹的研究多是关于有人机对地[3]、对空[4]。对无人机对地攻击的轨迹规划的研究[5]，侧重于分析地面威胁与编队的协同飞行，针对空战机动目标的无人机协同攻击轨迹研究较少。

本文分析了有人机/无人机协同攻击模式，从而定义了有人机/无人机协同发射区；有人机、目标和导弹采用三自由度仿真模型计算，同时构建无人机截击的矢量三角形，提出了无人机的截击策略，针对黄金分割法在搜索边界过程中可能陷入的死循环，提出了改进措施，在此基础上搜索了发射区的远近边界，并探究了目标的参数对发射区边界的影响。

1 有人机/无人机协同下空空导弹发射区概念

1.1 单平台空空导弹允许发射区

单平台空空导弹允许发射区以攻击机为参考，满足一定攻击条件下，攻击机发射导弹能以一定的概率命中目标的目标初始位置的范围[6-7]。发射区主要由发射平台与导弹的参数决定，该发射区以攻击机为中心，表示能以一定的概率命中目标的目标初始位置构成的三维空间区域。

1.2 有人机/无人机攻击模式

有人机/无人机协同攻击模式，就是在将要接敌的情况下，无人机凭借自身体积小，速度快的特点，迅速前突，随后在协同条件下，由传统的单机发射/制导发展成为在数据链路支持条件下，有人机探测跟踪，无人机发射，有人机制导的新攻击模式。其主要的特点在于：有人机探测跟踪目标，无人机利用机间数据链接受目标数据，对目标发射空空导弹。

1.3 有人机/无人机协同下空空导弹发射方式

因此，有人机/无人机协同下的空空导弹发射方式与传统的平台瞄准主要存在导弹形成发射条件和导弹的发射/制导方式两点不同。

1.3.1 导弹形成发射条件

导弹能否形成发射条件由“载机是否稳定跟踪并截获目标”和“目标是否进入导弹允许发射区确定”[8]。对于进行攻击的载机而言，前者与机载雷达性能密切相关，后者与空空导弹的攻击距离、机动能力相关。

无人机/有人机协同下，有人机利用雷达对目标探测、跟踪和截获，无人机根据有人机的信息发射导弹，实现了探测跟踪与武器发射平台的分离。

1.3.2 导弹的发射/制导方式

在有人机/无人机协同攻击模式下，传统单机发射/制导的攻击模式，发展成为无人机发射/有人机制导的攻击模式。该模式下，由有人机对目标进行探测、跟踪和截获，并通过机间数据链路共享目标信息，由无人机发射空空导弹，有人机对目标持续照射，进行中制导。

1.4 有人机/无人机协同下空空导弹发射区

结合上述条件，可以定义有人机/无人机协同下空空导弹发射区为在有人机无人机协同条件下，当满足攻击条件时，攻击机或者无人机发射空空导弹可以命中目标机的初始位置。该发射区是无人机和有人机攻击区的叠加。

2 运动模型的建立

2.1 有人机运动参数方程

以有人机为例，建立有人机的运动参数方程。

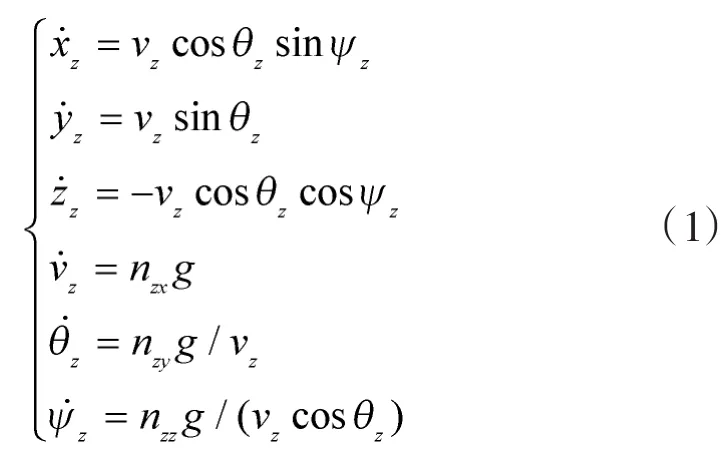
同理，可以参照有人机的运动参数方程，建立目标运动参数方程和无人机运动参数方程。

2.2 空空导弹运动参数方程

F、P和m的变化规律为：

式中，ρ为大气密度，Sm为弹体有效面积，Cm为导弹阻力系数，msec为燃料秒流量，m0为导弹初始发射质量，t0为导弹发动机工作最长时间。

2.3 相对运动参数方程

在研究导弹制导过程，有人机瞄准，跟踪以及无人机导弹发射的过程中，通常使用目标-有人机，目标-无人机，导弹-有人机视线坐标系的相对运动方程。

下面以目标-有人机为例，建立相对运动方程。

2.4 导弹制导参数方程

本模型导弹制导采用比例导引法，设在比例导引法控制下，导弹速度vm的方向变化率与导弹视线转率成比例[9]。即

式中，导引系数K（一般取3～5）需要满足机载导弹的收敛条件

其中，μ为机载导弹的前置矢量角。

导弹导引头通常存在最大跟踪角速度ωmax的限制：

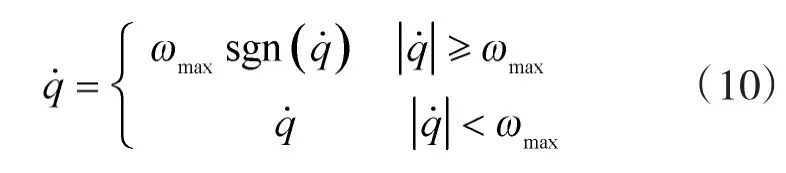
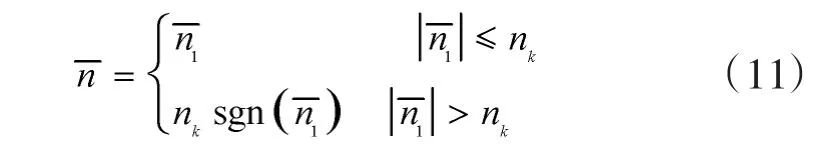
考虑舵机存在延迟[10]，则

式中，ni-1表示上一时刻的过载；为系统反应时间，通常取 =20 ms～30 ms，则当前时刻过载ni为

式中，△t为控制步长[1]。

2.5 协同发射区约束条件

在导弹飞行过程中，在某一时刻t，满足条件r＜e且t＞tj，则认为导弹命中目标，否则攻击失败，e代表允许脱靶量，tj为导弹解除引信时间。

同时导弹必须满足飞行高度限制、最小可控飞行速度限制、可控飞行时间限制、最大视场角限制约束：

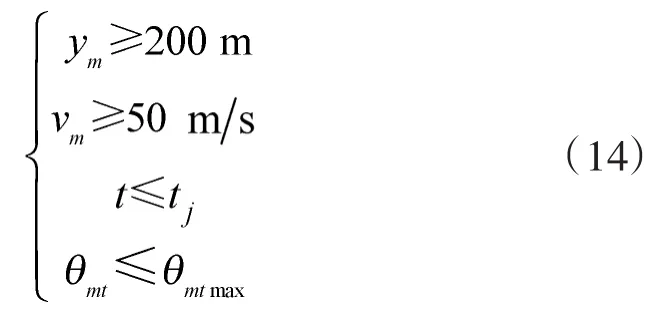
式中，θmtmax表示导弹的最大视场角。

2.6 编队有人机与无人机约束条件

同时有人机与无人机编队必须有人机探测距离约束、探测角度约束、编队协同最大距离约束、中制导距离和角度约束：

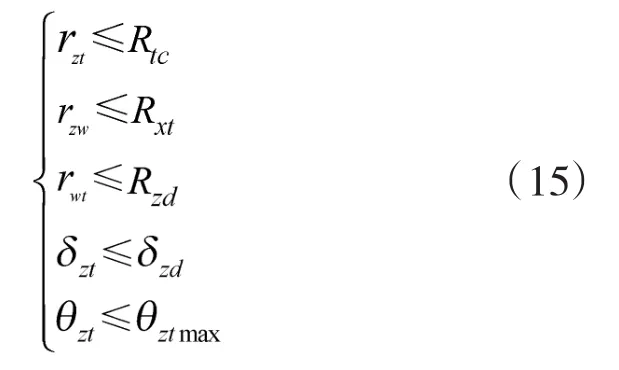
式中，Rtc表示最大探测距离，Rxt表示最大协同飞行距离，Rzd表示最大中制导距离，δzd表示最大制导角度，θztmax表示最大探测角度。

3 无人机机动策略选择

3.1 解决思路

当有人机或者战场预警系统发现目标后，无人机按照一定的机动策略截击飞行。首先根据空战态势，建立目标、无人机以及瞄准点构成的矢量方程，利用构成矢量三角形的关系，分解成标量方程组，然后综合考虑过载和导弹发射区限制，以时间最短为目标函数，求解出最优的攻击飞行轨迹。

3.2 建立模型

如图1所示，目标位于M0点，速度方向指向Ma匀速直线飞行，无人机初始点速度方向指向Ma，按照平行接近法，无人机可以在点发射导弹命中目标。设计无人机机动飞行轨迹为。

图1 无人机拦截飞行矢量图

符号说明：M0为目标的初始位置，Ma为初始目标瞄准点，Mb为实际目标瞄准点，W0为无人机初始位置，Wa为无人机机动节点a，Wb为无人机机动节点b，Wc为无人机武器发射点，Wd为初始无人机瞄准点，We为无人机预计武器发射点，D0为无人机与目标初始距离，Dd为无人机导弹射程，r为机动飞行的半径，q0为目标初始进入角，q1为无人机与目标线的夹角，α为目标线与基准线的夹角，θ为目标轨迹与无人机飞行轨迹夹角，ψ为导弹发射时目标线与基准线的夹角，T0为节点W0到Wa之间的时间，T1为Wa到 Wb之间的时间，T2为Wb到 Wc之间的时间，Tt为目标飞行到Ma的时间，Td为Ma到Mb的时间，Vp为无人机飞行速度，Vt为目标飞行速度，无人机机动过载为n，重力加速度为g，建立矢量方程：

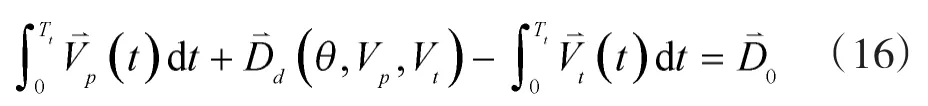
根据矢量方程和三角形的相关性质，可得标量方程：

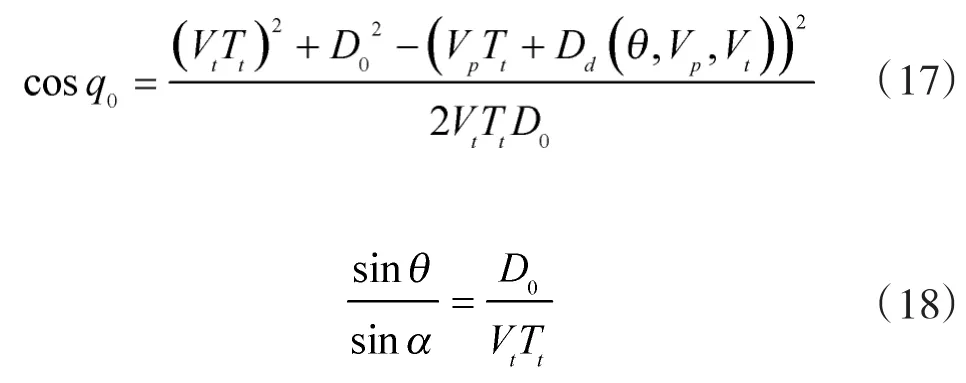
联立、可求解 Tt、q0。

初始位置W0到机动节点Wb转弯半径r为

3.3 模型的约束条件

飞行时间约束：无人机的飞行轨迹由初始节点W0到初始无人机瞄准点Wd变为先从初始节点W0进行机动飞行，至机动节点Wb，再直线飞行至导弹发射点Wc，这要求后者增加的飞行时间满足，为目标从初始瞄准点Ma到实际目标瞄准点Mb的时间。令，得

利用MATLAB仿真分析ρ与η、β其关系如下页图2，截取ρ≥1的部分，得到图3。

选取曲线上部的点ρ（η、β）≥1，即可满足约束条件。

图2 约束变量ρ与η、β的关系

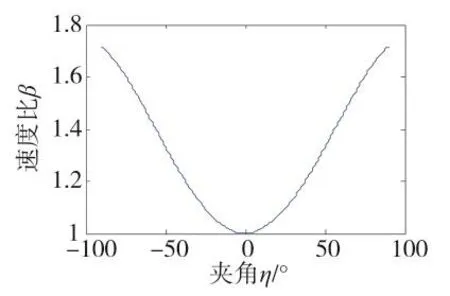
图3 约束变量ρ=1与η、β的关系曲线

3.4 截击策略仿真对比

假设空战态势如下，无人机与有人机协同飞行，在初始距离为D=100 km时发现目标，无人机开始加速前置飞行，无人机行驶速度为Vp=600 m/s，初始与目标线夹角为η=0°，目标进入角为q=60°，选取无人机初始点与初始瞄准点所在直线为基准线，无人机最大可用过载为nT=8 g，假设目标匀速直线飞行，目标运动速度Vt=350 m/s，无人机最大探测角为ψ=60°，导弹发射距离由计算的无人机/有人机协同下的导弹发射区求得。

图4 导弹拦截的初始阶段机动轨迹

表1 无人机过载与拦截时间关系表

结果表明，目标做匀速直线运动时，在该拦截方式下，过载对导弹拦截时间影响较小。

改变初始距离，观察在比例导引攻击轨迹与该模型攻击轨迹的拦截时间。得到一组结果，其部分结果如表2所示。

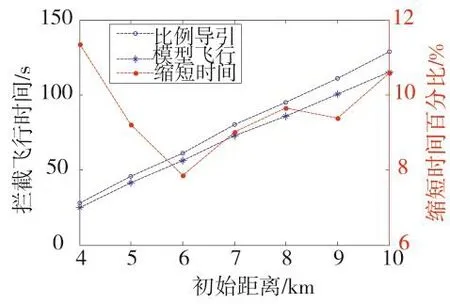
图5 两种攻击轨迹的攻击时间对比

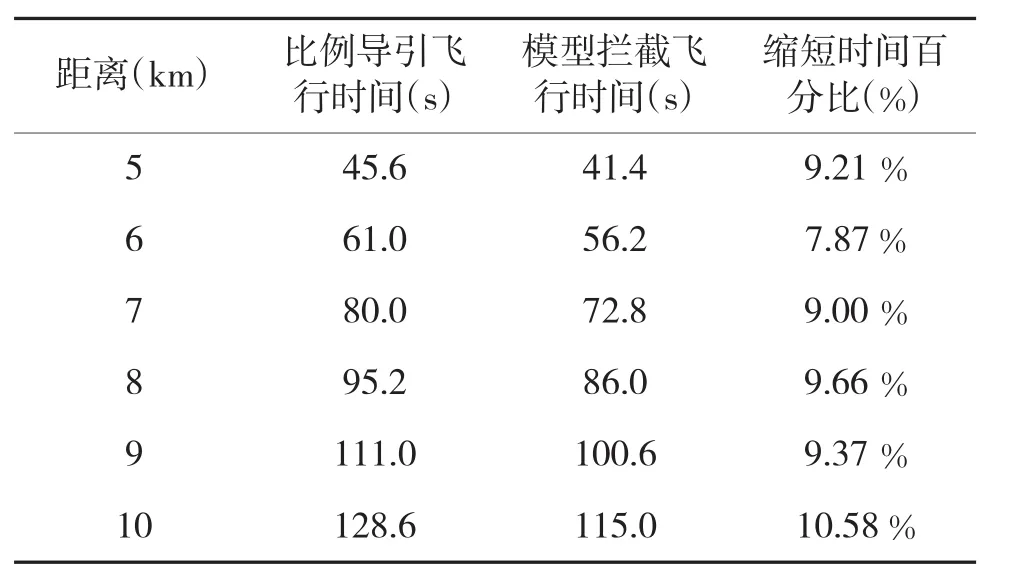
表2 目标距离与拦截时间关系表

改变目标的进入角，对比结果如图6所示。

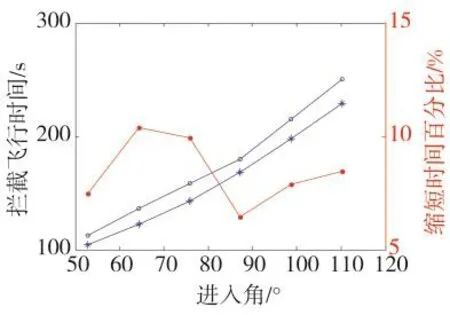
图6 两种攻击轨迹的攻击时间对比

其部分结果如表3所示。

表3 目标进入角与拦截时间关系表

图5、图6结果表明，该模型的拦截飞行比比例导引法飞行时间更短。截击飞行的时间越长，缩短的时间越多，其比例在8%左右。

4 有人机/无人机协同导弹发射区仿真

求解有人机无人机的协同发射区，先搜索周围空间，判断目标在某一初始位置，若无人机发射空空导弹，能否命中目标。仿真首先建立以有人机为中心的极坐标系，然后给定无人机的坐标，无人机的坐标根据目标位置求解，接着对有人机的周围区域，采用一维黄金分割法[11-12]，搜索导弹攻击近距离边界和远距离边界。

4.1 黄金分割法

4.2 缺陷及改进

黄金分割法要正常迭代，计算远边界时，初始点必须大于近边界，否则其远边界值会趋近与0，计算近边界时，初始点必须小于远边界，否则其近边界会趋近于无穷大。这是因为，载机的不可发射区分为近距不可发射区和远距不可发射区，通常由近至远依次为近距不可发射区，发射区，远距不可发射区，而黄金分割法只能在某一不可发射区与发射区之间搜索，当初始点落到另一不可发射区时，就会陷入死循环。

图7 近边界黄金分割法计算流程图

如图7所示，以近边界为例描述其改进方法：

2）在计算近边界时，如果该轮循环中曾命中目标，此时，如果在命中时，取；否则令。若未命中过目标，取。

4.3 仿真流程图

根据图8所示的仿真流程图，对无人机/有人机协同下的导弹发射区进行仿真计算。

图8 发射区计算仿真流程图

5 结果及分析

数值仿真计算条件：

1）目标飞行速度为100 m/s，做匀速直线飞行。

2）机载导弹发动机工作时间为8.4 s，导弹最大供电时间为26 s，导弹引信解锁时间为2 s，导弹杀伤半径为5 m，导引头最大视场角为60°。导弹初始质量为300 kg，燃料秒流量为10 kg/s，平均推力为6 200 N，最大机动过载为18 g。

3）无人机前置飞行速度500 m/s，载机飞行速度为200 m/s。

仿真1：目标进入角q=0°，无人机高度h=5000m，对比无人机前置飞行15 s与未前置飞行时的导弹发射区。

图9 进入角q=0°，高度h=5 000 m发射区

图9在水平面与垂直平面内，无人机/有人机的协同发射区远界增加；攻击的目标高度越低，导弹可以获得的能量越大，因此，下边界的攻击边界减小慢，攻击的距离相对更远。

仿真2：目标进入角q=200，无人机高度h=5 000m，对比无人机前置飞行15 s与未前置飞行时的导弹发射区。

图10 进入角q=20°，高度h=5 000 m发射区

图10结果与上面相似。但由于目标存在进入角，因此，无人机前置发射导弹对发射区左右两侧的增益不相同，目标速度指向的一侧发射区面积小，发射区距离减小快。

仿真3：目标进入角q=0°，无人机高度h=6000m，对比无人机前置飞行15 s与未前置飞行时的导弹发射区。

图11结果显示，无人机前置飞行时，无人机高度增加，对于导弹上界增益较大。

图11 进入角q=0°，高度h=6 000 m发射区

表4选取了不同参数下的发射区远边界值。目标与载机迎头飞行时，有人机/无人机协同攻击，能使该仿真条件下的导弹发射区扩大43%左右。

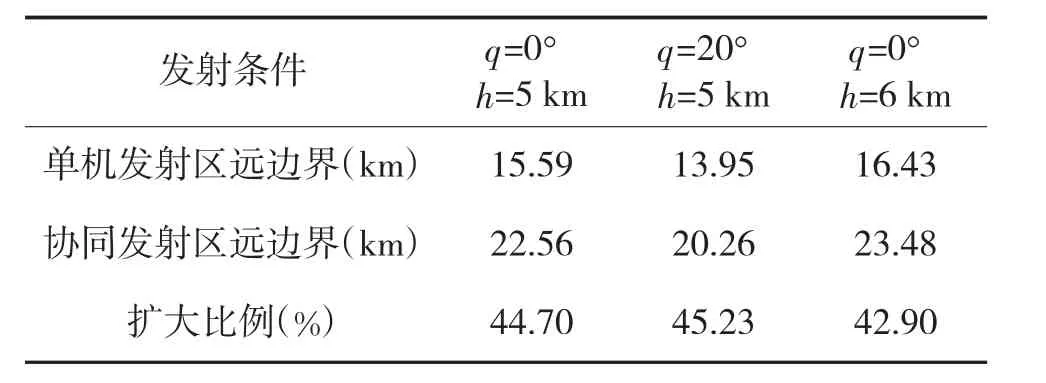
表4 迎头条件下导弹发射区远边界

6 结论

本文定义了无人机/有人机协同态势下的空空导弹发射区，提出了一种攻击模型，相比比例导引飞行，具有更短飞行时间。仿真计算出协同攻击区，结果明显大于传统攻击区，为有人机/无人机协同作战的决策提供了依据。