弹簧储能密度理论研究

陶元芳，刘亚倩，高友山

1 引言

能源与环境问题是当今社会面临的最严重的问题之一。如何减少能量损耗、储存能量，实现循环利用从而减轻环境和资源的负担成为人们关注的焦点[1]。储能是通过能量之间的相互转换，将能量储存在质量或体积中的过程。弹簧储能是通过弹簧的压缩或拉伸将外力做功转换成弹簧的变形能，将能量储存在变化的弹簧体积中[2]。储能密度作为衡量储能技术水平的主要指标，对研究储能效率具有重要作用。

2 定义

储能密度：利用各种物质或各种手段，在一定的空间或质量物质中储存起来的可利用能量，即单位质量的储能量或单位体积的储能量。因此，储能密度包括质量储能密度和体积储能密度[3]。

3 弹簧储能

弹簧储能的基本原理是：利用弹簧的变形将外界做功转换为弹簧的弹性势能储存起来。弹簧质量储能密度：在弹簧不产生塑性变形的条件下，弹簧在最大压变形量时的储能总量与弹簧总质量的比值[4]。弹簧体积储能密度：在弹簧不产生塑性变形的条件下，弹簧在最大变形量时的储能总量与弹簧的最大体积的比值[5]。

3.1 拉伸弹簧储能

拉伸弹簧工作过程中，主要受限于材料的许用应力[6]。

拉伸弹簧的极限拉力：

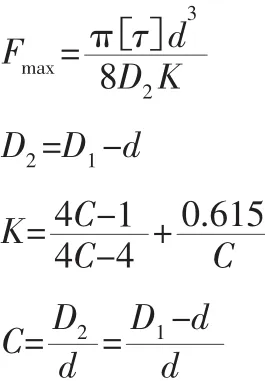
代入得：

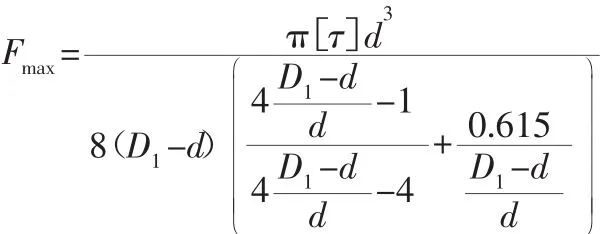
式中：Fmax—弹簧能承受的极限拉力（N）；

［τ］—许用切应力，（MPa）；

K—曲度系数；

D2—弹簧的中径（mm）；

d—弹簧材料的直径（mm）；

D1—弹簧的外径（mm）；

C—旋绕比。

由上式可以看出，在许用应力范围内，拉伸弹簧的极限拉力受弹簧丝直径和弹簧外径的影响。弹簧的极限拉力的关系，如图1所示。

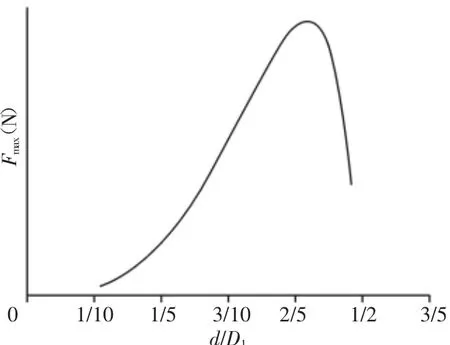
图1 极限拉力变化曲线Fig.1 The Change Curve of Maximum Tensile Force

极限拉力下的变形量：

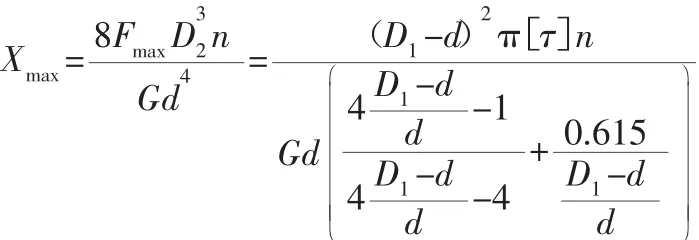
式中：Xmax—极限拉力下的变形量（mm）；n—弹簧的圈数；G—切变模量（MPa）。

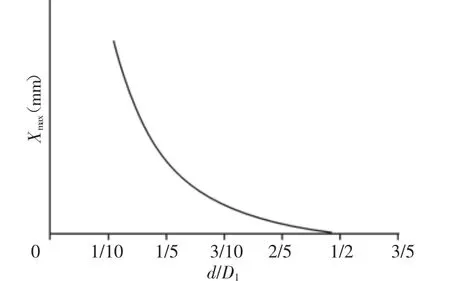
图2 变形量变化曲线Fig.2 The Change Curve of Deformation

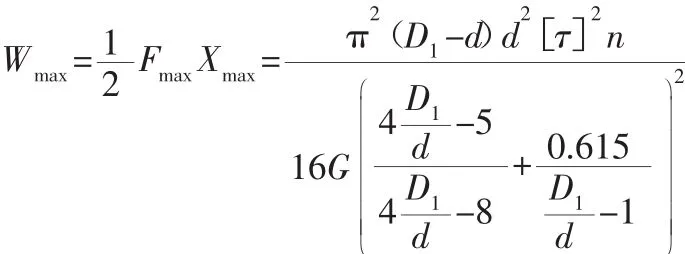
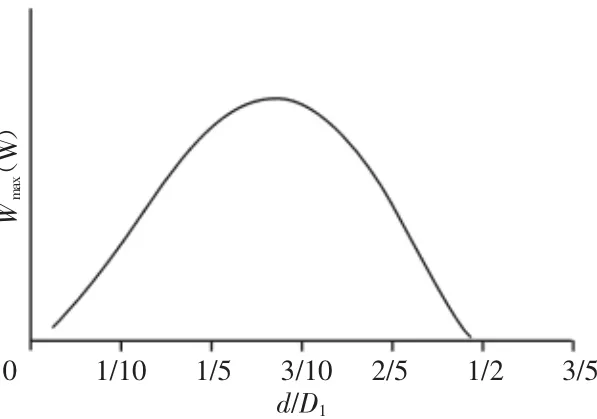
图3 变形能变化曲线Fig.3 The Change Curve of Deformation Energy

由图3可以看出，弹簧的圈数和外径不变时，弹簧的变形能随着弹簧丝直径的增大先增大后减小，最大值出现在处。

质量储能密度：

式中：m—弹簧的质量（kg）；l—弹簧丝的总长度（mm）；l1—弹簧的钩部展开长度（mm）；ρ—弹簧材料的密度（kg/mm）。代入得：

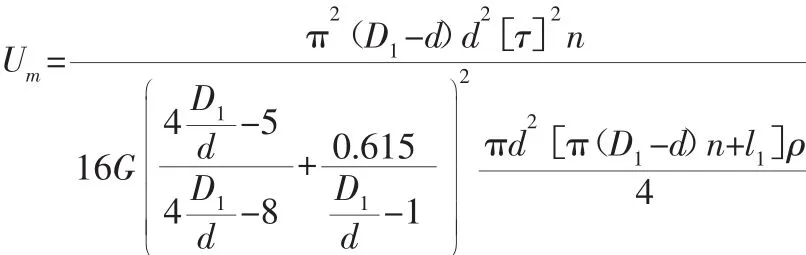
以LⅠ型拉伸弹簧为例：

l1=2×0.5πD2=π（D1-d）

所以质量密度：

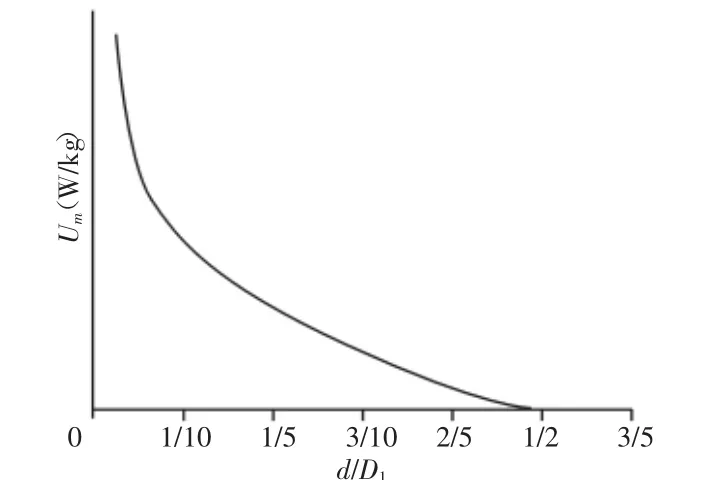
图4 质量储能密度变化曲线Fig.4 The Change Curve of Mass Energy Storage Density

体积储能密度：

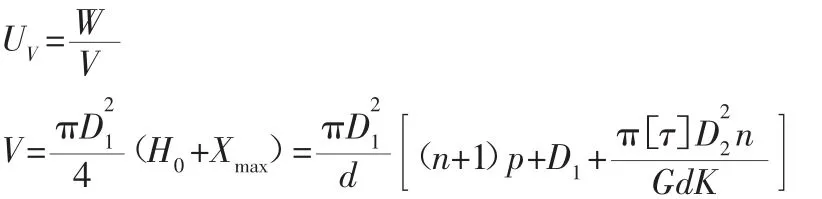
式中：V—弹簧的体积，（mm3）；H0—弹簧的初始高度，（mm）；p—弹簧的节距（mm）。

代入得：

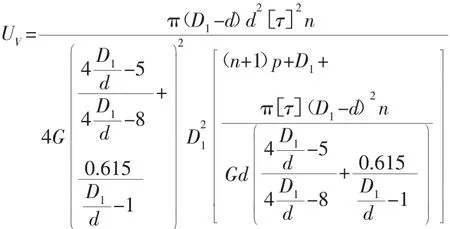
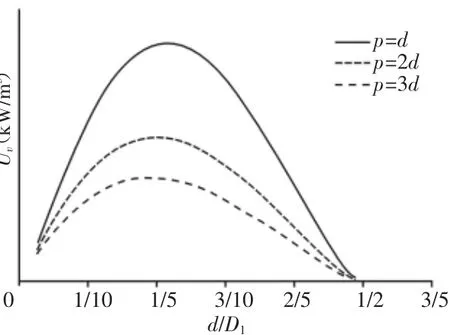
图5 体积储能密度变化曲线图Fig.5 The Change Curve of Volume Energy Storage Density

3.2 压缩弹簧储能

（1）压缩弹簧与拉伸弹簧不同，压缩弹簧会出现弹簧圈压紧的状态。因此，在研究压缩弹簧的储能密度时，要考虑两种情况：（1）压紧状态：弹簧处于压紧状态时产生的工作切应力τ＜［τ］，此时不受许用应力的影响，弹簧的压缩量最大；（2）极限状态：弹簧压紧时，如果τ＞［τ］，压缩弹簧与拉伸弹簧相似，在压缩过程中受许用应力的影响，受力达到最大值[6]。

①压紧状态

式中：n1—弹簧的总圈数，（n1=n+1.5）；

②极限状态

弹簧能够承受的极限压力：

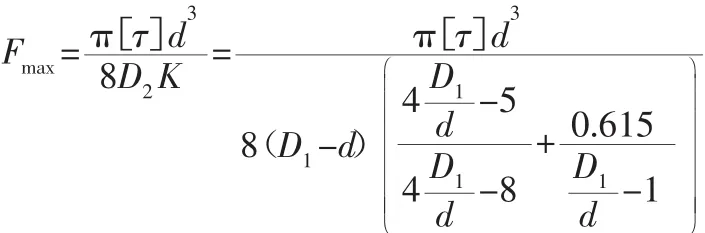
极限压力下的变形量：

（2）曲线分析

当弹簧的体积固定（外径与初始高度不变）时，弹簧丝直径和节距对弹簧的变形量、力、变形能、质量储能密度和体积储能密度的影响曲线，如图6～图10所示。图中：·表示两种状态的分界点，分界点之前是压紧状态，分界点之后是极限状态。

①变形量

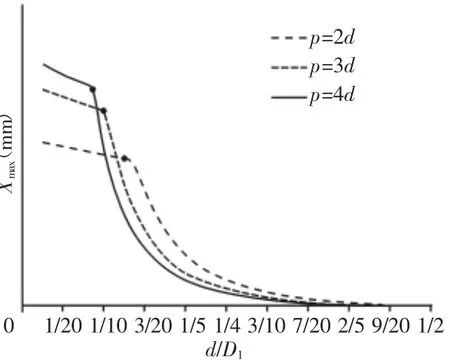
图6 变形量变化曲线Fig.6 The Change Curve of Deformation

不同弹簧丝直径和不同节距对弹簧变形量的影响曲线，如图6所示。弹簧丝直径越大，弹簧的刚度越大，弹簧的变形量越小[7]。压紧状态下，弹簧丝直径相同的弹簧，节距越大弹簧的变形量越大；极限状态下，弹簧的压缩量受到许用应力的限制，弹簧的节距越大，弹簧的压缩量越小。

②压力曲线

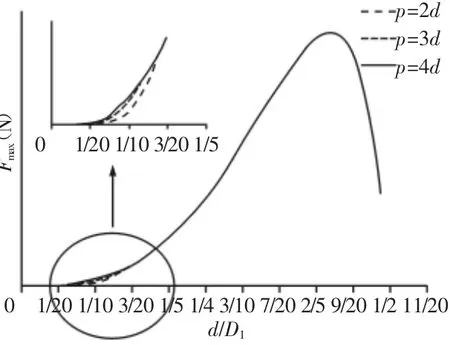
图7 压力变化曲线Fig.7 The Change Curve of Force

由图7可以看出，随着弹簧丝直径的增加，压力呈现先增后减的趋势。压紧状态下，压力受弹簧节距的影响，弹簧丝直径相同的弹簧，节距越大压力越大；而极限状态下，弹簧的压力不受节距的影响。

③变形能曲线

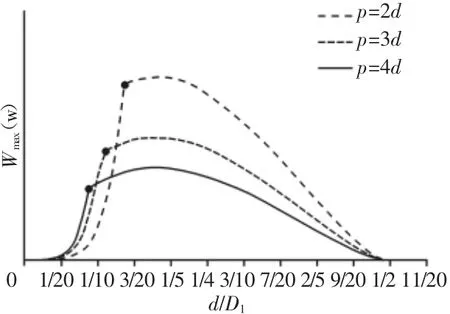
图8 变形能变化曲线Fig.8 The Change Curve of Deformation Energy

由图8可知（1）压紧状态下，弹簧丝直径越大，弹簧的变形能越大；弹簧丝直径相同弹簧，节距越大，变形能越大[7]。（2）极限状态下，随弹簧丝直径的增加，变形能先增后减；而且，弹簧丝直径相同的弹簧，节距越大，变形能越小。变形能的最大值通常出现

④质量储能密度

图9 质量储能密度曲线图Fig.9 The Change Curve of Mass Energy Storage Density

由图9可知（a）压紧状态下，弹簧丝直径越大，弹簧的质量储能密度越大。（b）极限状态下，随弹簧丝直径的增加，质量储能密度先增后减，最大值通常出现在弹簧丝直径相同的弹簧的质量储能密度都随节距的增大而减小。

⑤体积储能密度曲线

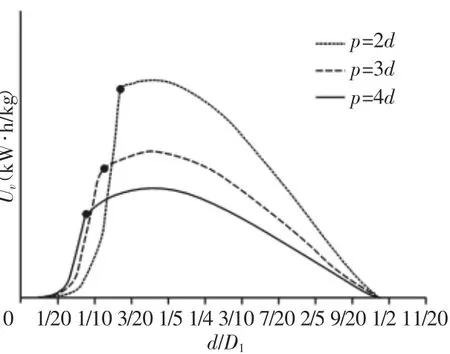
图10 体积储能密度变化曲线Fig.10 The Change Curve of Volume Energy Storage Density

由于弹簧的最大体积是不变的。所以弹簧的体积储能密度的变化趋势与变形能的变化趋势相同。

在满足弹簧丝直径的基础上，压缩弹簧的储能密度受节距的影响，节距p对Um的影响和UV的影响相反，因此p的选择应综合考虑，通常p的值选在4左右[8]。

（3）实例

①拉伸弹簧

弹簧外径D1=40mm，材料许用切应力［τ］=706MPa，切变模量 G=78.5GPa，材料密度 ρ=7850kg/m3。

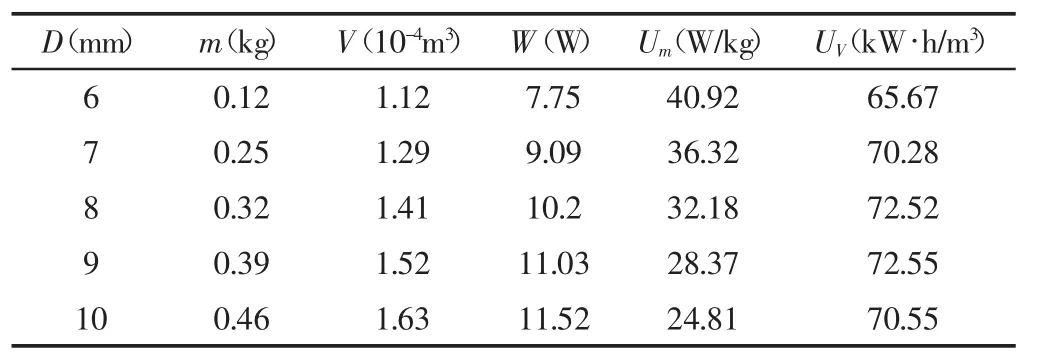
表1 拉伸弹簧的储能密度（P=d）Tab.1 The Energy Storage Density of Tensile Spring（P=d）

1节5号电池的电量为1.8W，也就是说此弹簧的最大变形能相当于4到5节5号电池的能量。

②压缩弹簧

弹簧外径D1=40mm，初始高度H0=132mm，材料许用切应力［τ］=706MPa，切变模量 G=78.5GPa，材料密度 ρ=7850kg/m3。

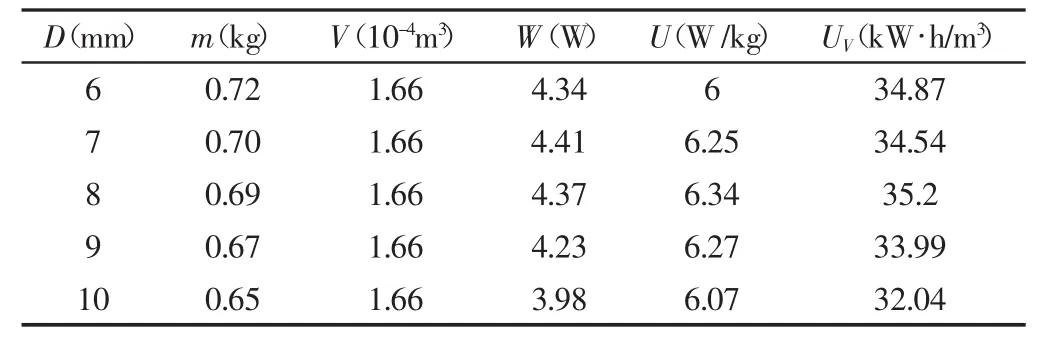
表2 P=4d时弹簧的变形能和储能密度Tab.2 The Energy Storage Density of Compression Spring（P=4d）

此弹簧大最大变形能相当于2.5节5号电池的能量。

4 结论

（1）无论是拉伸弹簧还是压缩弹簧，变形能、质量储能密度和体积储能密度的最大值都出现在因此，要想提高弹簧的储能效果，就要在满足许用应力的前提下，。（2）在满足弹簧丝直径的基础上，拉伸弹簧节距越小储能密度越大[9]。（3）而对于压缩弹簧而言，综合考虑质量储能密度和体积储能密度，取p=4d最合理。（4）弹簧的储能密度相对于其他储能装置而言是比较小的[10]。