考虑多因素的一步矿房采场跨度优化

东龙宾 王少泉 张 华 周 育 何 祥

（1.中冶北方（大连）工程技术有限公司，辽宁大连116000；2.安徽马钢张庄矿业有限责任公司，安徽六安237400）

采用充填法进行开采可有效控制地压、防止地表沉降和预防岩爆。目前越来越多的大型深部金属矿山采用充填法进行开采，而采用充填法开采时，如何确定合理的采场结构参数，一直是现场工程技术人员关注的热点，国内外学者也对采场结构参数优化进行了多方面的研究。许多研究者采用层次分析法与模糊数学综合评价方法对采场结构参数进行评价［1-5］，但未涉及遗传算法的研究。例如李洁慧等［1］针对影响采场结构参数选择的复杂因素，提出了一种基于层次分析法和模糊数学的综合评价方法。杨建［4］根据残矿资源技术分类和技术条件，运用模糊数学和层次分析法的基本理论，对4种备选开采模式方案进行综合评判优选。许多研究者也通过遗传算法优化获得最优采场结构参数［6～10］，但未涉及考虑多个因素并基于AHP和模糊综合法获得不同采场结构参数的综合评价指标的研究。例如王星星［6］利用遗传算法全局搜索能力得到最合适的采场结构参数，并从岩体力学参数随机性角度分析了其稳定性的可靠度。尚振华等［7］对采场结构参数进行了多种方案的FLAC3D数值模拟，采用神经网络和遗传算法对模拟结果进行选择、优化，确定了最佳的采场结构参数。王洪武等［10］提出了一种基于正交有限元—模糊可靠度—遗传算法的采场结构参数优化设计分析方法。徐帅等［11］基于正交试验方法设计了16种模拟方案，运用FLAC3D进行数值计算，并通过建立SOM模型，获取了最佳采场结构参数。许多学者也从能量释放率角度对采场结构参数进行了研究［12-13］，但未涉及本项目中胶结充填率、能量释放率、屈服率以及顶板拉应力区率多种指标的研究。

在上述研究的基础上，本研究对不同采场跨度参数的优劣采用胶结充填率、能量释放率、屈服率及顶板拉应力区率4种评价指标，并采用层次分析法和模糊评判法获取综合评价指标，再利用遗传算法计化出最优的一步矿房采场跨度。

1 工程背景

张庄铁矿矿体为隐伏状，一期开采-210～-450 m阶段矿体，首采阶段为-450 m阶段，二期开采-450～-690 m阶段，综合生产能力500万t/a。采矿方法为大直径深孔阶段空场嗣后充填法，阶段高度60 m，沿矿体走向每108 m划分为一个盘区，每个盘区内划分为5个采场。阶段空场嗣后充填法开采每个阶段衍生了2个步骤，将矿体间隔划分成2种类型的矿房，即一步矿房回采单元和二步矿房回采单元，开采一步矿房时，二步矿房作为矿柱用于保证一步开采时的稳定性；一步矿房开采结束后采用胶结充填作为二步矿房的人工矿柱，二步矿房回采结束后用全尾砂充填。对于岩体条件较好的矿山，采场跨度是制约采场稳定性的重要因素。

当一步矿房跨度小于二步矿房跨度时，可降低充填材料的成本，且在开采一步矿房时，二步矿房的应力量值相对较小，有利于侧帮的稳定性。但是，二步矿房跨度的提高则造成二步矿房顶板的暴露面积增大，不利于采场稳定。由于现场铲运机的限制，矿房的跨度不能小于15 m。因此，对于一个盘区内的5个矿房，其二步矿房的跨度则不能超过18.5 m。在上述限制条件下，本项目探讨了如何对一步矿房跨度进行优化。

2 计算模型与开采步骤

计算模型如图1、图2所示。为了便于调整矿房的尺寸，采用了六面体网格，并利用八叉树网格加密技术来使得岩层界面周围网格加密。模型选取的是8#剖面，跨度为200 m，包含研究的对象盘区和其相邻2个盘区的一半。模型的底部设置为x、y、z3个方向的位移约束，4个侧面采用法向位移约束，采用摩尔—库伦本构模型。充填体和岩体力学参数均通过试验，并结合现场结构面调查结果折减获得。由于-180 m之上基本为第四系，而地表的标高平均为+30 m，因此模型的顶部均设置为应力边界条件，应力值为4.2 MPa。

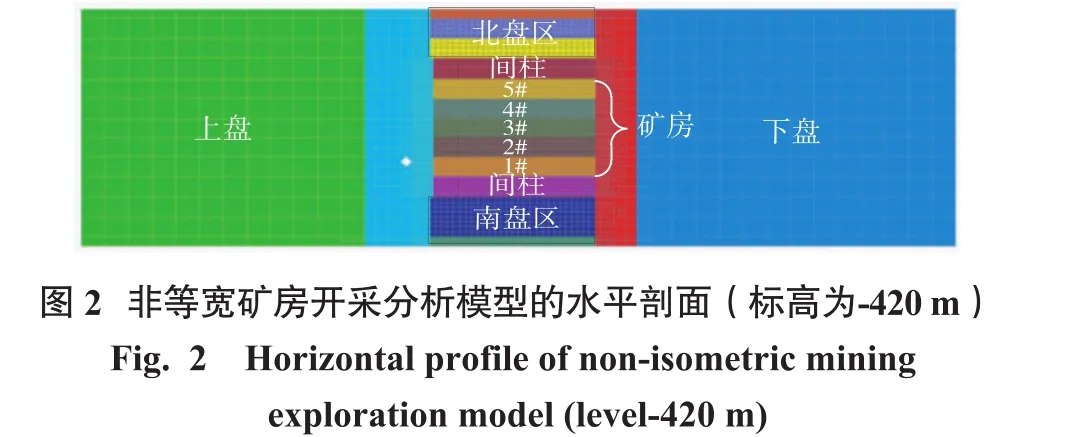
盘区共分为5个矿房，其中1#、3#和5#为一步矿房，其跨度变化在15～16.4 m之间，2#和4#矿房为二步矿房，其跨度变化在16.4～18.5 m之间。开采的顺序为1#、5#、3#（一步矿房）和2#、4#（二步矿房）。在开采对象盘区之前，先将南北的相邻盘区开采并充填。

3 不同采场跨度的计算结果

3.1 相关评价指标

对地下开挖工程如隧道、硐室的稳定性指标，主要有能量指标、位移指标、强度指标。由于地下采矿的采场跨度较大，顶板的冒落对下部的人员和机械危害较大，因此还需加上顶板拉应力区指标。以上几个指标描述如下：

（1）围岩和胶结充填体能量释放率RRE。能量释放在一定程度上反映了岩石工程结构的稳定状态，主要取决于开挖岩体的速率和体积，通常用能量释放率RRE作为系统稳定的指标。因此，可将能量释放率RRE定义为系统释放的总能量与开挖体积之比。在利用FLAC3D进行计算时，每一步开采围岩的总能量E：

式中，fix、fiy和fiz分别为开采表面上第i个节点x、y和z方向的等效节点力，kN；Δix、Δiy和Δiz分别为对应的诱发位移增量，m；n为开采表面的节点数。基于上述能量释放率指标，RRE为

式中，V为开采矿体的体积，m3。

（2）采场围岩和充填体平均屈服率RAF。采场围岩和充填体都有可能发生塑性破坏。这里提出平均屈服率RAF的定义如下：

（3）采场顶板拉应力区率RTF。

3.2 不同采场跨度计算结果

利用FLAC3D计算了一步矿房跨度分别为16.4 m、16.0 m、15.7 m、15.4 m、15.0 m的开采方案，为了衡量不同一步矿房跨度的每个因素的优越性，能量释放率取5个矿房开采的平均值，屈服率也采用5个矿房开采的平均值，由于一步矿房开采的拉应力区非常小，而往往二步矿房开采拉应力区更受关注，因此拉应力区率为二步矿房开采的平均值。

以上3个因素及胶结充填率随一步采场跨度的变化见图3～图6。胶结充填率属于经济因素，其显然随着一步采场跨度减小而线性减小；能量释放率随一步采场跨度减小而增大，但变化不明显；屈服率随着一步采场跨度减小而减小。

上面的4个因素，能量释放率和顶板拉应力区率随着一步矿房跨度增大而越有利，胶结充填率和屈服率随着一步矿房跨度减小而越有利，此时无法判定到底是一步矿房越大越好还是越小越好，下面将引入层次分析法和遗传算法进行打分和优化。

3.3 分析方法与一步采场最优跨度的确定3.3.1 层次分析法确定权重向量

层次分析法的层次结构分别为方案层、准则层和目标层。面对方案的决策问题，要比较n个因素x1、x2、…、xn对目标的影响。通过两两比较的方法将各因素的重要性量化，两个因素的比较，最能比较出它们的优劣程度。每次取两个因素xi和xj，用正数aij表示两者的重要性之比。全部比较结果得到的矩阵A=（aij）n×n，该矩阵为成对比较矩阵也称正互反矩阵。依据比较的标度和判定原理，用数字1～9作为标度，其数值见表1。

?

注：标度值2、4、6和8分别为两等级之间的中间状态。

为了使判断结果更好地与实际状况相吻合，需进行一致性检验，判断比较矩阵A一致性的检验公式为CR=CI/RI，其中CI为一致性检验指标，CI=（λmax-n）/（n-1）。RI为随机一致性指标（取值见表2）。若CR＜0.1，则认为比较矩阵可以接受。

?

求比较矩阵A的最大特征值λmax对应的特征向量W，单位化W即可得出每一个因素对应的权重。胶结充填率、能量释放率、屈服率、拉应力区率这4个因素对应的比较矩阵为

上述比较矩阵的λmax为4.058 3，那么CI=0.019 4，得出CR=0.021 6＜0.1，一致性可以接受，对应的4个因素的权重分别为0.057 9、0.131 4、0.504 6和0.306 1。

3.3.2 收益性指标和消耗性指标

定量指标可分为收益性指标和消耗性指标。对于收益性指标，值越大越好；对于消耗性指标，值越小越好。目标的相对隶属度公式：收益性指标：ri=yij/max（yij）；消耗性指标：ri=min（yij）/yij。

影响采场跨度的4个因素均属于消耗性指标，通过无量纲化处理后如表3所示。

?

3.3.3 综合评价指标与遗传算法

将表3所示的消耗性指标与因素的权重相乘求平均就得到相应的综合评价指标，指标越大则方案越优。对于任意跨度采场的相关因素的消耗性指标则是通过这5个采场进行Hermite插值，而后利用遗传算法优化出最优的一步采场跨度。遗传算法（Genetic Algorithm，GA）［14］是一类可用于复杂系统优化的鲁棒性搜索算法，它是摸拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局概率搜索算法。如上所述，根据综合评价指标的倒数对采场跨度进行优化，如图7所示，获得的最优综合评价指标为1/1.046 19，对应的一步采场跨度为15 m。

4 结论

（1）研究表明，能量释放率和顶板拉应力区率随矿房跨度增大而减小，胶结充填率和屈服率随矿房跨度增大而增大。

（2）通过FLAC3D数值模拟获得不同一步矿房跨度的能量释放率、屈服率以及顶板拉应力区率，结合胶结充填率，进行综合指标判定，通过引入层次分析法和遗传算法优化，认为一步矿房跨度设为15 m最优。

（3）利用层次分析法，通过遗传算法优化获得了最优的采场结构参数，该方法避免了单因素决策的片面性和因素过多而难以分配权重的弊端，为非等宽采场结构参数的选择提供了理论基础，可用于其他类似矿山采场结构参数优化。