引入深度学习的城市基准地价评估模型研究

王 华，罗 平，张 杰

（1.国土资源部城市土地资源监测与仿真重点实验室，广东 深圳 518034；2.郑州轻工业学院计算机与通信工程学院，河南 郑州 450002）

城镇基准地价是指在城市特定区域内，根据土地用途、利用条件相似原则划分均质区域，并评估出各地价区段在某一时点的平均水平价格[1]。城镇基准地价成果能够反映土地市场的时空演变格局，并且对于土地资源优化配置及土地利用效益最大化具有重要意义[2]。

城镇基准地价与其影响因素之间存在着复杂的非线性映射关系，很难通过某种确定的数据模型来准确描述和表达。中国在基准地价评估工作实践当中常用的方法包括算术平均模型[3]、线性、指数等回归统计模型[4-7]，算数平均模型的缺陷在于其计算结果严重依赖于均质区域内样点的空间及数量分布情况，回归模型直接模拟土地级别与样点地价之间的数学关系进而确定某一级别基准地价，但该模型需要预先人为确定影响因素权值，具有很大的主观性、经验性与不确定性，导致其预测精度受到一定限制[8]。有研究人员尝试利用模糊数学[9-10]以及云模型[11]等方法来改进传统回归模型，但上述方法更为关注定性因素的评估量化，仍忽略了地价因素权值确定问题。部分学者认为地价样本空间分布不均衡，聚集或者稀缺现象均会出现，导致数据存在一定空间相关性，为消除变量本身的空间自相关对回归结果的影响，引入了Kriging空间分析法[12-14]来构建地价求解方程，但该方法也未考虑影响因素权重取值主观性这一问题。人工神经网络模型具有自主学习地价样本特征的优势，近十几年来在基准地价评估研究中获得广泛应用[15-18]。它不需要确定权重，克服了多因素权重确定主观性强的缺陷，并可利用多层神经网络建立地价与影响因素之间的映射关系。还有学者将支持向量机（Support Vector Machine, SVM）模型用于确定城镇基准地价评估，通过与传统回归模型及人工神经网络对比表明该方法在基准地价测算方面具有优越性[19]。无论是人工神经网络模型或者支持向量机都属于浅层学习算法，在训练样本及计算单元受限的情况下对城市地价及其影响因素之间的复杂函数的表示能力会受到一定制约[20]。

近些年兴起的深度学习技术由于拥有多层非线性映射网络层，使其获得较强的复杂函数拟合能力，在复杂分类、识别、预测等问题的解决中获得了广泛应用，并取得良好的效果和效率[21-22]。深度学习可以看作神经网络的发展，Hinton等[23]认为深层神经网络结构可以学习到对象更深刻更本质的特征。因此本文尝试选择深度学习的经典算法深度置信网络[24]（Deep Belief Network, DBN）来构建城镇基准地价评估模型，并以湖北省武汉市基准地价评估为实例，对基于深度学习的城镇基准地价评估模型的建立流程及模型优化方法进行了探讨和研究。

1 基于深度学习的城镇基准地价评估模型

1.1 深度置信网络理论

1.1.1 深度置信网络结构

深度学习是一类新兴的多层神经网络学习算法，通过多隐层感知器来组合低层特征形成更加抽象的高层表示，自动地学习得到层次化的特征表示，从而有助于提高分类和预测的准确性。DBN是由若干层受限玻尔兹曼机（Restricted Boltz-mann Machine,RBM）及一层反向传播网络（Back-propagation, BP）组成的一种深层神经网络，其基本思想是采用无监督学习方法逐层训练每一个RBM，最后对整个网络采用有监督学习进行微调。

1.1.2 受限玻尔兹曼机

受限玻尔兹曼机（RBM）是一种特殊的玻尔兹曼机，由一个可视层（v）和一个隐含层（h）组成，可以看作为一个二部图，两层之间通过权重w连接，同层单元之间无连接。

由图2中可以看出，可视层中任一可见节点vi和隐含层中隐含节点hj之间都存在一条权值为wij的连接，且wij=wji，0＜i＜m，0＜j＜n。令b表示可视层偏置量、c表示隐含层偏置量。RBM网络是对称结构，因此可利用式（1）、式（2）互相计算可视层及隐含层节点值。

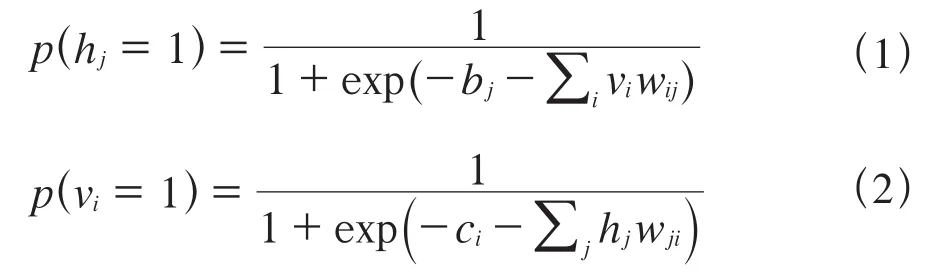
对于一个二值化信号（v1，v2，…，vm），利用式（1）可以计算得到一个相应的隐含特征信号（h1，h2，…，hm），对于给定的状态（v，h），RBM的节点状态满足玻尔兹曼分布，其能量函数可以定义为：

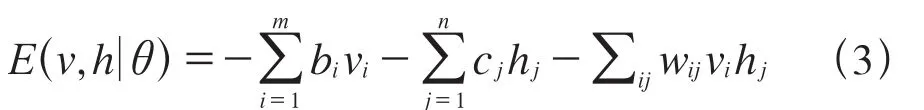
那么，状态（v，h）的联合概率分布为：

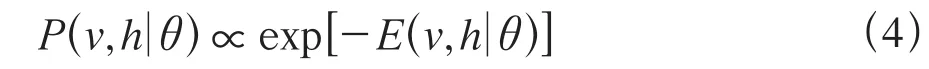
RBM进行无监督学习的目的就是通过吉布斯抽样不断调节θ= （w，b，c）参数，最终使得联合概率P（v，h|θ）最大，即使得隐含特征信号h还原重建成v′后与v之间误差最小。为使状态（v，h）趋向平稳，需要通过计算最大P（v，h|θ）与初始状态的联合概率的斜率Δθ来引导参数θ更新，其计算公式如下所示：

式（5）中：τ表示最大迭代次数；η为学习速率。由于难以确定概率变化斜率计算的步长，对比散度（Contrastive Divergence, CD）算法[25]被提出用于加速RBM训练过程并保持了精度。

1.2 深度置信网络地价评估模型

1.2.1 城市基准地价评估问题描述

城市基准地价受自然、经济、区位等多种因素影响，评估结果既能够表现出自然经济因素影响土地价值的区域结构性特征，也能反映人文活动及其他因素对地价的随机性扰动。城市基准地价评估问题实质就是在对自然经济影响因素作用量化的基础之上，利用评估模型构建起地价与多维特征之间的复杂映射关系。

对于城市基准地价评估问题，样本特征即为评估模型的输入，将样本特征数据集X表示为

式（6）中：L为样本数据集数量（1≤l≤L）；D为每个样本数据的特征个数（1≤d≤D），每一个拥有D个特征的数据都可以看做是空间RD中的一个向量，即X中的一行；xdl为第l个样本的第d个特征值，表示第l个样本地块在某一个属性特征上的量化值；Y为与样本特征数据集对应的样本标签数据集，可以表示为式（7）；yl表示第l个样本地块对应的实际市场价格。

城市地价评估的核心即为寻找映射X→Y的问题。由于特征维数较高，映射关系通常会非常复杂，通过机器学习方法，特别是深度学习方法能够对这类问题进行较为准确的求解。基于该映射网络可以将各级别评估单元的特征向量分别输入获取到评估单元地价，再通过加权或者取平均值的方法即可求取某一级别的平均地价即基准地价。

1.2.2 模型的建立

选择DBN网络来建立城市地价评估模型，它由输入层、多层RBM和BP微调层构成，输入层为土地价格影响因素xl，输出层为评估地价yl。城市地价评估DBN模型的建立流程如图1所示。

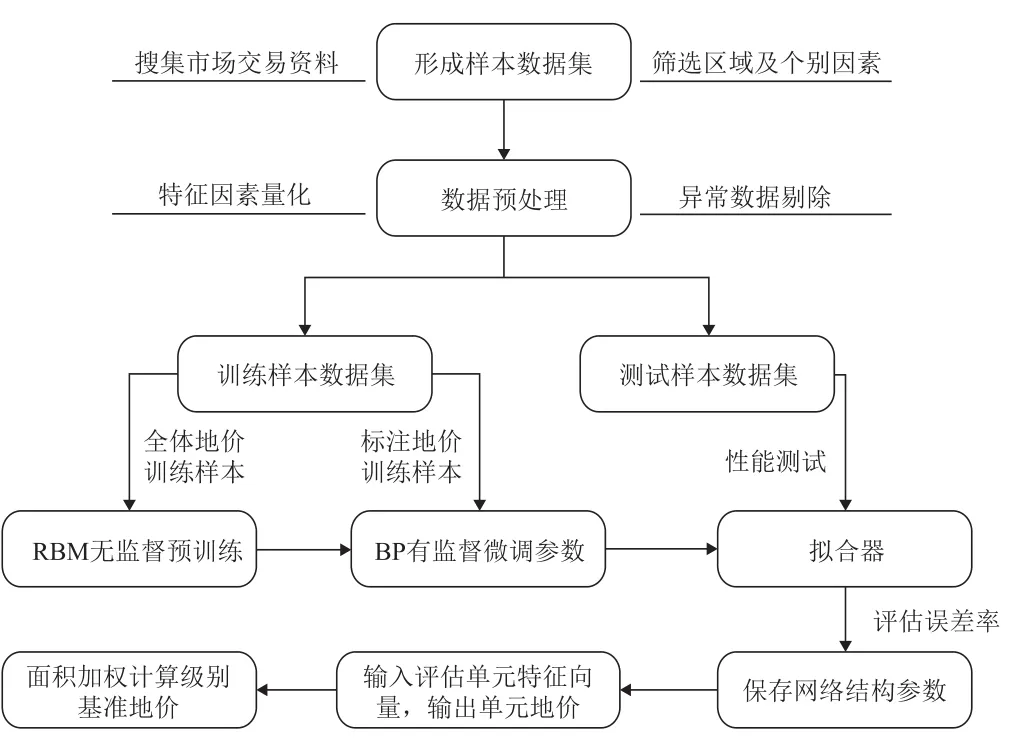
图1 城市地价评估模型的构建Fig.1 Construction of appraisal model for urban land benchmark price

（1）采用z-score方法对样本集特征数据进行归一化预处理，如式（8）。

式（8）中：z为归一化后的数据特征值；x为某一具体分数；φ为平均数；σ为标准差。

归一化的目的：一是为满足DBN算法对输入特征数据格式的要求；二是消除不同量纲的影响从而避免部分特征无法有效参与地价评估。

（2）将原始样本集合按照设定比例随机拆分为训练样本集合（Xtrain，Ytrain）和测试样本集合（Xtest，Ytest），并给定所有样本的地价标签Y。

（3）样本预训练。以全体训练样本数据集的D维特征向量作为输入，采用逐层的无监督贪婪学习的方法来训练模型中的RBM。在每一层，可视层H及隐含层V单元的状态按照式（1）和式（2）进行计算，参数空间（w，b，c）可按照式（5）进行更新。

（4）微调。基于监督学习机制对最后一层的BP网络进行训练，将最后一层RBM的隐含输出作为BP网络的输入向量，基于BP的反向传播机制利用误差反馈信息对整个DBN网络参数进行微调，直到迭代次数达到设定值为止。

（5）测试及评估。将测试样本数据集输入到训练好的DBN，利用模型的输出地价与样本标签地价计算得到平均评估误差率λ（式（9）），并将其作为衡量DBN评估性能的标准。

式（9）中：ytest表示测试样本的实际地价；Ntest表示测试样本集合的数量；y′表示模型的输出地价。

（6）计算评估单元地价。继续对评估单元进行特征量化，并同样按照式（8）进行归一化，并输入到训练好的DBN网络之中，可计算得到每一个评估单元的地价。

（7）计算基准地价。本模型选用面积加权法，利用每一级别内的评估单元的地价及对应的面积权重进行基准地价计算，如式（10）。

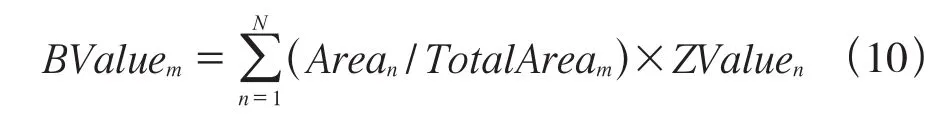
式（10）中：BValuem表示第m级别的基准地价；Arean表示m级别内第n个评估单元的面积；TotalAream表示级别m的所有单元的面积之和；ZValuen表示利用模型求取的第n个评估单元的地价。

2 实例分析

2.1 数据采集与处理

本文以湖北省武汉市主城区土地定级及基准地价更新项目为依托，以商业用地基准地价评估为例，利用多因素综合评定法划定商业用地评估单元2 110个，并将单元划分为4个土地级别。课题组收集商业地价样本点共12 386个，通过对样本点的异常检验，对其异常数据进行纠正或剔除，经整理后保留有效样点共9 568个，然后对修改后的样点进行统一编号和规范化处理并入库备用，按样点的具体位置落实到定级单元图上。在利用样本点评估基准地价之前，根据交易情况、交易期日、使用年期、容积率等因素对样点地价进行修正。

一般而言，影响城市商业用地价格的因素有交通条件、繁华程度、人口状况、地形、城市规划、基础公用设施、环境质量等特征因子。本文在武汉市基准地价评估成果基础之上，以主导性、定量化等为指导原则，并结合现有研究[4，17]最终确定武汉市商业用地评估因素体系，共计18个评价因子，如表1所示。将上述评价因子作为DBN网络的输入因子，其量化后的作

用分值作为网络输入，经过修正后的样点地价作为网络输出。

为衡量特征因子对样本点的影响程度，本文需要搜集土地利用、地形、交通条件、区位条件、基础设施配置、环境状况等方面的资料及空间图件来进行空间量化分析，因子作用分值计算及对评估单元的空间量化方法均参考《城镇土地分等定级规程》。土地利用数据及地形数据来源于武汉市国土资源局提供的土地变更调查数据、土地利用更新调查和第二次土地调查数据库；道路通达、汽车站等交通数据主要参考交通部门提供的道路等级图、道路分布图、交通图等资料；大气污染、绿地覆盖等数据来源于环保部门；医院、电讯、供排水等数据来源于市政部门。

表 1 商业用地评估指标体系Tab.1 Index system for urban commercial land appraisal

2.2 实验设置

将样本点集合中的9 568个地价样本点全部进行标注，随机抽取其中8 000个样本作为估价模型的训练样本，剩余的1 568个作为测试样本验证模型性能。为验证DBN模型的评估性能，本文还实现了两种不同网络结构参数的BP神经网络评估模型，分别定义为BPANN1和BPANN2，此外将SVM模型也设置为对照试验。DBN 隐含层数目设置为3，即总层数为5层，每层的神经单元数依次为18、15、8、4、1，将特征信号逐层压缩，最后形成4 维特征向量进行拟合。DBN模型无监督训练阶段学习率为 0.6，迭代次数为 200，为动态调整学习率设置初始动量项参数为0.5，中后期调整为0.9。BP神经网络考虑两种情况，BPANN1设置为单隐层结构，隐含层神经单元个数采用遍历法确定，遍历区间为[1，25]，经搜寻后将隐层单元设定为12个。BPANN2则采用和 DBN一样的网络结构即18-15-8-4-1；DBN的监督学习阶段和两个ANN的训练方式一致，均采用梯度下降算法，学习率为0.4，迭代 200 次。SVM取核函数为高斯径向基核，利用6折交叉验证和网格法遍历寻找到最优的惩罚因子C为100，径向基核函数参数σ为6.4。

2.3 评估性能分析

考虑到多层神经网络参数的随机性，将上述3种算法各运行20次，并统计对应的输出误差及相对误差，结果见表2。

表2 不同评估模型的测试结果Tab.2 Test results of different appraisal models

由表2的结果可以看出DBN模型的平均相对误差比BPANN1、BPANN2、SVM三个模型分别要低2.13%，4.36%，1.05%。相比于BPANN1、SVM模型，DBN的深层架构明显能够更好地挖掘地价样本集的深层特征，其将原始的22维特征抽象成了4维高阶特征进行评估，能够获得比浅层结构更好的拟合精度。此外，DBN与BPANN2模型的网络结构及监督训练阶段的参数设置虽然均保持一致，但两者的拟合精度却相差较多，这是由于DBN模型利用其无监督贪心算法有效地对网络结构参数进行了预训练，显著提高了模型的拟合精度。BPANN2的网络结构参数一般是通过随机化方法来进行初始化，然后通过该网络进行训练，其参数未经过有效优化，所以对样本集合的地价拟合精度较差，DBN与BPANN2的监督训练过程如图2所示。此外，BPANN2的网络结构虽然要复杂于BPANN1，但由于传统训练及反馈系统的误差传播效应导致其复杂参数系统影响整体网络系统的拟合功能，所以其拟合精度反而要比BPANN1低2.23%。SVM的目标函数是一个凸函数，可以保证得到问题的全局最优解，避免了人工神经网络优化频繁陷入局部最优的困扰，所以其拟合精度要比BPANN1高1.08%。

传统的浅层学习方法一般仅依靠监督训练来优化模型参数，当训练样本不足时，模型评估性能不够理想。但本文DBN模型包括RBM无监督训练和BP有监督训练两个训练阶段，理论上来讲可以在样本较少时依然获得较高的拟合精度。本文通过从样本集合中抽取少量训练样本来测试各个模型在训练样本数量不足时的评估性能。在各模型参数设置同上的情况下，从9 568个标注样本中分别抽取400、800、1 200、1 600、2 000个样本作为训练样本，剩余的作为测试样本，各模型的测试相对误差如表3所示。

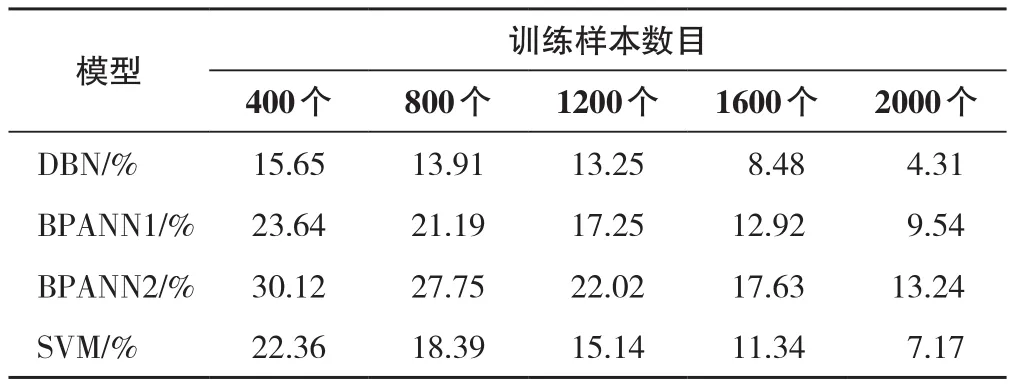
表3 不同训练样本数目的测试结果Tab.3 Test results of appraisal models for training with different numbers

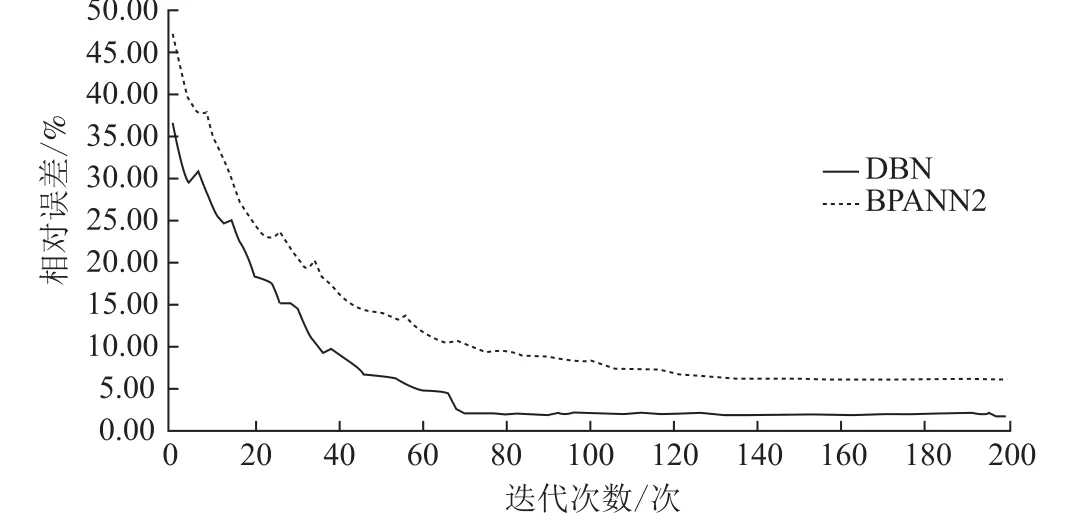
图2 DBN和BPANN2的监督训练过程Fig.2 Supervised process of DBN and BPANN2

根据表3测试结果可以看出，在训练样本数量较少的情况下，DBN模型显示出了比BPANN1、BPANN2、SVM模型明显更优越的评估性能。当训练样本数量仅为400时，DBN的相对误差值比上述三个模型低了7.99、14.47、6.71个百分点。随着训练样本数量的递增，各个模型的评估精度都增长明显，DBN模型在训练样本数量为1 600时，拟合精度提高到91.52%，而样本数量为2 000时，拟合精度已经可以达到95.69%，仍然比其他模型的拟合精度高出2.86～8.93。SVM模型的评估精度虽然低于DBN但却显著高于BPANN1和BPANN2，这是由于其基于结构风险最小化的训练框架能够在一定程度上客服训练样本不足的问题，但是BP神经网络是基于经验风险最小化的模型，在训练样本数量不足时，网络参数无法得到有效优化，因此其评估精度较低。DBN通过对无标签城市样本数据的非监督训练来进一步抽象样本集合特征，使得网络结构参数尽量靠近最优区域，因此在有监督训练阶段即使通过少量标注样本的训练也可使模型获得较高的评估精度。综上述所，DBN模型在训练样本数量不足时依然可获得较为理想的评估精度。

上述实验一定程度上说明了DBN的无监督训练过程对于模型评估性能的重要性，本文继续通过改变参与无监督训练的地价样本数量来探讨DBN地价模型评估精度的变化规律。首先固定有监督训练微调阶段的标注样本数量为1 000，然后分别设置RBM无监督训练段的无标签训练样本数量为500、1 000、1 500、…、5 000，每一种参数设置的模型分别运行5次然后求取平均相对误差如图3所示。

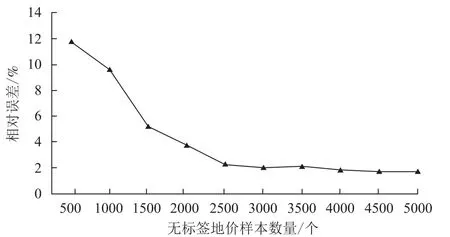
图3 DBN相对误差Fig.3 Relative error of DBN

由图3可以看出，随着无标签地价样本数量的增加，DBN模型的测试相对误差逐渐降低，即评估精度越来越高，当加入3 000个无标签样本时，评估精度达到了97.92%。从曲线变化趋势来看，在无标签训练样本数从500到2 500的过程中，DBN的评估准确率上升较快，之后的增加趋势较为平缓。总体来看，充分的无监督训练可以有效改善深层网络结构参数，为监督训练微调提供优化后的网络结构，进而提高模型整体的评估精度。

表4 各级别基准地价Tab.4 Different classes of urban land benchmark prices

在因子作用体系下，构建各级别评估单元的特征向量矩阵，并将其输入DBN的深层网络结构，可输出所有评估单元对应的地价，然后运用式（10）可计算得到各级别的基准地价，计算结果见表4。

3 结论

本文针对城市基准地价评估问题，提出一种基于深度置信网络的城市地价评估方法。以湖北省武汉市基准地价评估为实例，得出以下结论：

（1）与BPANN1、SVM这类浅层学习模型相比，DBN的深层网络结构明显能够更好地挖掘城市地价样本集的深层特征，通过将原始的22维特征抽象成4维高阶特征进行评估，获得了比浅层学习方法更好的评估精度。

（2）DBN比具有同样网络结构的BPANN2地价评估精度要高出4.36%，本模型借助其无监督贪心算法能够有效对网络结构参数进行预训练，而BPANN2采用随机化方法生成网络参数，所以其评估精度较差。

（3）在训练样本不足时，DBN对于城市地价评估任务仍然能够获得较为满意的评估精度，相比于其他模型其评估优势更为明显，这得益于DBN的非监督训练阶段能够尽量优化网络结构参数，此外实验还证明了DBN 的无监督学习方法使其能够利用大量无标注样本显著提升评估精度。

本文首次将深度学习方法与城市基准地价评估问题相结合，为地价评估课题的研究提供了新思路。但由于深度置信网络算法的参数较为复杂，本文主要参考已有研究通过经验式的实验仿真选定的模型参数，但是并未能保证达到该算法求解地价评估问题的最大性能。其次在DBN训练网络下进一步求取了各级别均质区域的基准地价，但和现有研究[5，19]一样还缺少进一步论证的方法来证明该基准地价的准确性。