长三角城市土地稀缺与土地利用效率的交互影响

龙开胜，李 敏

（南京农业大学公共管理学院，江苏 南京 210095）

1 引言

基于现实存在的资源稀缺性，探究一个社会如何进行组织才能最有效地利用其资源、实现有效的资源配置[1]，是一个十分重要的议题。近年来中国城市化快速发展，城市人口迅速增长，建设用地大量增加，大多数城市土地资源，尤其是“后备”建设用地资源稀缺已经成为一个严峻的社会问题。为了缓解土地资源约束，为城市发展提供充足的资源和空间，无疑要提高资源的技术利用效率和社会利用效率[2-4]。但稀缺资源利用效率的提升，并不一定会缓解资源稀缺程度，因为资源利用效率提升会加速资源总量消费，反而会使资源更加稀缺，这在水资源、渔业资源等研究中得到证实[5-6]。对于城市土地而言，随着土地利用效率的提升，如果缺乏有效的城市外延控制措施的配合，城市人口和经济总量扩张必将导致城市建设用地数量迅速增长[7-9]，由此导致城市规划范围内可供给的建设用地不断减少，城市土地尤其是建设用地稀缺程度越来越高。同时，城市用地规模的持续盲目扩张，会对土地资源造成浪费，长此以往的发展不利于城市土地利用效率的改善[10]。因此，科学阐述城市土地利用效率和稀缺程度之间的关系，协调提升城市土地利用效率与限制城市土地面积扩张速度之间的关系是一个非常关键的问题。

为了更好地揭示城市土地稀缺和土地利用效率的相互作用，本文以长江三角洲城市土地为研究对象，借鉴传统城市土地利用效率和考虑非期望产出下的城市土地利用效率，探讨土地稀缺程度对于土地利用效率的影响，以及土地利用效率对土地稀缺程度产生的冲击等核心问题。由于长江三角洲城市群是中国城市土地剧烈变动和人口迅速聚集的热点地区[11]，城市建设用地“后备资源”紧缺，并且伴随着城市土地利用效率整体偏低的现象[12]，以这一区域为研究对象也具有典型性和代表性。

2 计量模型设置与数据处理

2.1 计量模型设置

土地利用效率的高低影响土地稀缺程度，土地稀缺度映射到土地投入上，反过来影响土地利用效率的高低。土地稀缺度和土地利用效率之间存在着联动关系。为了进一步探究两者之间的因果关系，采用向量自回归（Vector Auto Regression, VAR）方法，将土地稀缺度、土地利用效率两组变量作为一个系统进行分析，将系统中所有变量视为内生变量且允许存在不可观测的个体异质性（个体效应和时间效应）。但是VAR模型对数据长度要求较高，本文采用的数据是2003—2015年间的数据，不能满足其要求。因此，使用面板向量自回归（PVAR）的估计方法，该模型对时间序列的长度要求大大降低：如果以T为时间长度、以m为滞后项的阶数，那么当T≥m+3，就可以进行参数估计；而当T≥2m+2，就可以估计稳态下的滞后项参数[13]。借鉴Holtz-Eakin等的研究[14]，建立PVAR基础模型如下：

式（1）—式（2）中：Zait包含两个变量向量，即传统土地利用效率（用te1表示）和土地稀缺度；Zait-1表示滞后一期；Zbit包含两个变量向量，即考虑非期望产出土地利用效率（用te2表示）和土地稀缺度；Zbit-1表示滞后一期。估计步骤分为以下两步：

首先，进行面板协整分析和面板Granger检验。本文采用面板协整分析，将变量之间的短期波动和长期均衡结合在一起，以探究变量之间蕴含的长期均衡关系。为了进一步检验变量之间的相关性是否具有经济学和理论意义，对研究变量进行Granger因果检验。

其次，进行脉冲响应函数估计和预测方差分解。脉冲响应函数与方差分解是研究变量相互之间冲击的影响与反应的重要方法，两者互为补充。脉冲响应函数描述的是模型中某一内生变量的正交化新息对系统中其他内生变量的影响，可以通过各变量对冲击的动态反应情况。预测方差分解是将预测误差的来源分别归因于各变量的正交化新息（也称为新息核算），以评价每一个结构对内生变量变化的贡献度[15]。

面板协整分析与面板Granger检验、脉冲响应函数估计和预测方差分解均可运用stata 14.0软件完成。

2.2 数据处理

2.2.1 土地利用效率指标

通常来说，土地利用效率可以简单阐述为投入产出的比值；从环境约束角度看，可以考虑产出中的“副产品”即非期望产出，提出对土地利用效率产生负面影响的因素，从而获得更为贴近实际情况的效率值[16]。分别测算传统土地利用效率（te1）（即未考虑非期望产出，仅从基本投入产出角度测度的土地利用效率）、考虑非期望产出的土地利用效率（te2）（即剔除工业生产中具有负面效应产出的土地利用效率）。为了便于比较，本文选取了相同的指标。从劳动力、资金和土地生产要素投入角度出发，建立如表1所示的评价指标。

表1 土地利用效率评价指标体系Tab.1 Indexes of land use ef fi ciency assessment

本文首先采用基于产出导向的CCR模型的DEA（数据包络分析）方法测算te1[17]。在CCR模型中，假设有n个决策单元，每个决策单元都有m种类型的输入和s种类型的输出，记输入向量Xj=（x1j，x2j，…，xmj）T，产出向量Yj=（y1j，y2j，…，ysj）T。设决策单元的投入产出为（Xj0，Yj0），记为（X0，Y0），则该模型的一般表达式为：

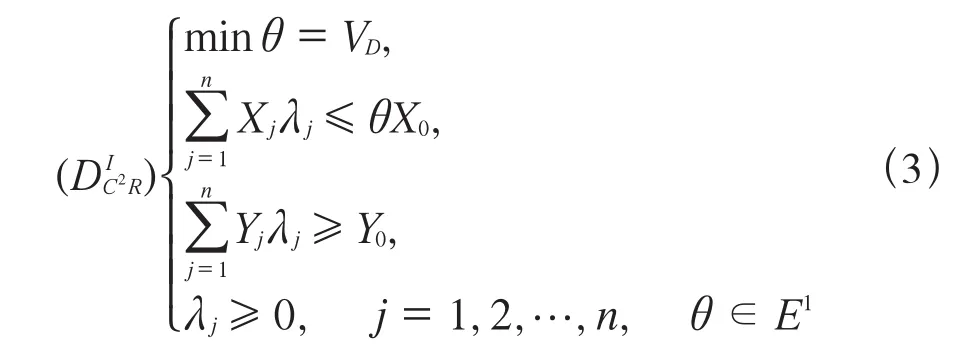
式（3）中：θ为技术效率评价指数，也就是投入和产出的相对效率值；VD代表最小技术效率值；λj为投入和产出的权向量。

其次，考虑工业废水、二氧化硫、烟尘等主要工业污染物对城市环境效益产生的负向影响，将其作为城市土地经济活动引入效率评价模型中。采用1997年Chung构建的方向性环境距离函数测算te2[18]，假设在城市土地利用过程中投入用Z表示，产出分为两种，其中期望产出为Y，非期望产出用X，产出水平的期望方向为G=（Y，-X），即尽量增加Y而减少X[16]。函数公式如下：

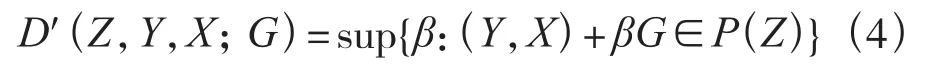
式（4）中：P（Z）表示生产可能性集合；β表示期望产出Y增加、非期望产出X减少的最大可能性数。其中P（Z）可以表示如下：

在式（4）的基础上，可以得出包含非期望产出的技术效率公式：

传统土地利用效率和考虑非期望产出的土地利用效率均可用DEA-SOLVER Pro5.0软件进行计算，并且在这些分析之前要对变量的平稳性进行检验。

2.2.2 土地稀缺度指标

中国城市土地市场和公共政策的不完善削弱了土地市场反应的效率[19]。城市建设用地资源的日趋紧张充分体现出土地资源对城市经济增长的约束，尤其是城镇密集的东部沿海地区[4]。在已有研究中，城市土地稀缺度的衡量多采用城市建设用地面积与国有建设用地供应总量的比值、城市建成区面积与建设用地审批面积比值等。但是，建设用地审批面积、国有建设用地供应总量等行政规制色彩太强，与当前城市建设用地的市场化趋势存在一定的脱节。为了克服这个问题，使得土地稀缺度和土地利用效率之间具有内在一致性，本文基于现实人均建设用地规模和标准人均建设用地规模差异角度衡量城市土地稀缺度状况。若实际人均建设用地规模超出国家标准规定的阈值，则建设用地规模不合理，城市扩张受到限制，引发城市土地稀缺程度高等一系列问题。城市土地稀缺度计算公式具体如下：

式（7）中：LT为城市人均建设用地规模现状；LS为国家规定的城市建设用地规模标准；S为城市土地稀缺度。因为城市扩张在一定时期内具有较强的惯性，人均建设用地规模针对性强，能很好地体现人口增长影响下的城市土地需求[20]。采用人均建设用地规模与标准的比值作为土地稀缺度的衡量指标，充分结合了城市建设用地的市场化趋势以及人口快速增长背景下的土地利用现状。城市建设用地标准中人均建设用地规模标准是一个范围值，为了方便比较，本文均选择各区间内的最低值。

2.2.3 数据说明

本文采用长三角26个地级及以上城市2003—2015年面板数据，其中二三产业从业人员、建成区面积、工业废水排放量、工业二氧化硫排放量、工业烟尘排放量、城市人均建设用地规模指标来源于2004—2016年《中国城市统计年鉴》，固定资产投资、非农GDP来源于2004—2016年《中国统计年鉴》。为了消除价格影响，非农GDP指标以2003年为基期，采用GDP平减指数进行数值平减。针对城市建成区面积、建设用地面积个别年份数据缺失的情况，进行插值处理。另外，本文指标数据均选取市辖区数据，因为市辖区代表了城市的主体，人口密度更大，经济贸易更发达，更能反映城市的特征，土地稀缺性也更高[7]。

2.2.4 数据平稳性检验

土地稀缺度和土地利用效率是根据大量宏观经济数据计算出的结果，随时间变化的趋势明显。为确保数据的平稳性，消除异方差的影响，本文对土地稀缺度序列、土地利用效率序列进行对数化处理，并采用Levin-Lin-Chu（LLC）和Im-Pesaran-Shin（IPS）检验面板数据的平稳性。当两种检验方法的结果均表明序列稳定时，才判断序列是平稳的。传统土地利用效率对数（lnte1）、考虑非期望产出的土地利用效率对数（lnte2）以及土地稀缺度对数（lnsca）的单位根检验结果是不平稳的，故对这些数据进行一阶差分后进行单位根检验。结果显示，一阶差分后的dlnsca、dlnte1和dlnte2已经是平稳序列，即3组变量均是一阶单整。

3 长三角城市土地利用效率与稀缺的关系研究

3.1 城市土地利用效率与土地稀缺度的协整分析与Granger因果检验

尽管土地稀缺度对数（lnsca）与传统土地利用效率对数（lnte1）、考虑非期望产出的土地利用效率对数（lnte2）序列是非平稳的，但仍可能具有长期均衡关系。数据平稳性检验结果说明3组变量均是一阶单整的，符合协整分析前提条件。协整分析结果显示dlnsca和dlnte1、dlnsca和dlnte2均显著拒绝原假设，说明传统土地利用效率、考虑非期望产出的土地利用效率与土地稀缺度之间均存在协整关系，即存在长期均衡关系。

协整分析的结果表明，lnsca与lnte1、lnsca与lnte2之间均存在协整关系，但是并不能说明这种相关关系是否具有经济学和理论意义，因此需要运用Granger因果关系检验做进一步分析。检验结果说明dlnsca分别是dlnte1、dlnte2的Granger原因；反过来，dlnte1、dlnte2均不是dlnsca的Granger原因可以揭示土地效率和土地稀缺之间存在单向的因果关系。

3.2 最优滞后阶数确定与模型稳定性检验

为了提高估计效率，获得最优脉冲响应函数和预测方差分解结果，保证结果的有效性，需要进行确定模型估计的最优滞后阶数，并对模型估计的稳定性进行检验。

本文综合考虑AIC、BIC、HQIC信息准则，采用连玉君的stata软件程序包（PVAR2）进行滞后项的选择[21]（表2）。模型1和模型2估计的最优滞后阶数均为2。

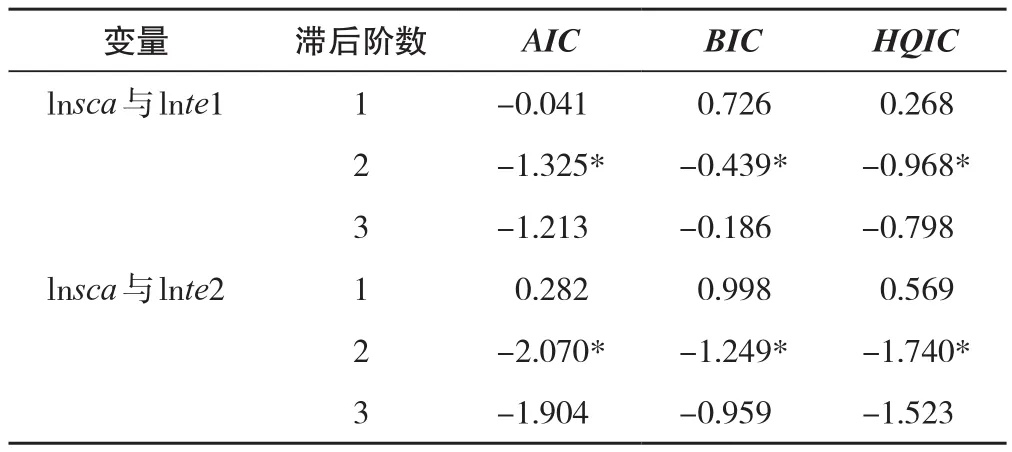
表2 滞后项选择标准Tab.2 Selection criteria of delay item

本文主要采用INESSA LOVE提供的PVAR程序得到模型1和模型2稳定估计及检验结果[22]。其结果显示PVAR模型的全部根的倒数值均位于单位圆内，因此模型估计是稳定的，可以进行脉冲响应分析和方差分解。

3.3 城市土地利用效率与土地稀缺度的脉冲响应分析

尽管Granger因果检验说明城市土地利用效率与土地稀缺度之间存在单向因果关系，但是只是一种动态相关关系，表明的是一个变量是否对另一变量有“预测能力”。因此需要进行脉冲响应对变量之间的影响趋势做进一步验证。根据Granger检验结果，在脉冲响应分析中应该按照lnsca～lnte顺序对变量进行排序，并将考察冲击作用的期限设为10期。图1、图2汇总了Monte Carlo模拟500次的脉冲响应函数图。

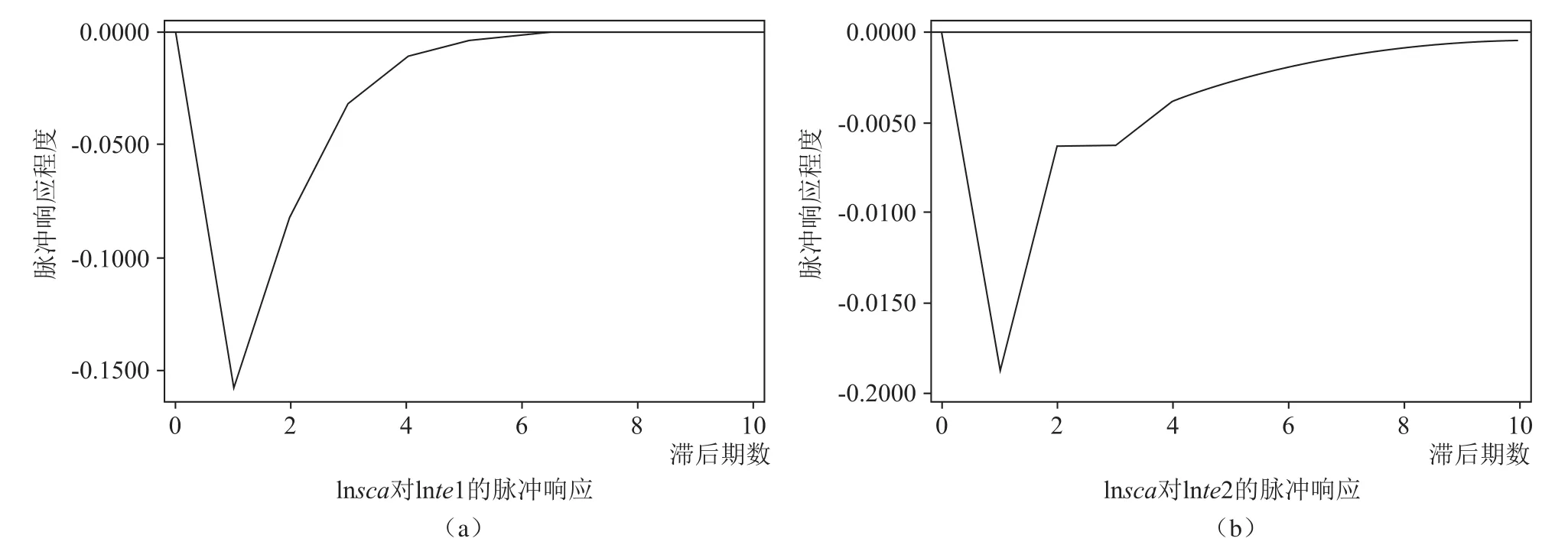
图1 lnsca对lnte1、lnte2脉冲响应比较Fig.1 Comparison of IRF of lnsca to lnte1 and IRF of lnsca to lnte2

图2 lnte1、lnte2对lnsca的脉冲响应比较Fig.2 Comparison of IRF of lnte1 to lnsca and IRF of lnte2 to lnsca

两种土地利用效率对土地稀缺度的冲击总体上均表现出先上升后下降的负向累积效应，但是影响持续时间区别较大。从图1中分析出具体脉冲响应情况为： 对于1个标准差传统土地利用效率（lnte1）冲击，土地稀缺度（lnsca）体现为负向影响，并在滞后1期影响程度明显增长，累积效应为到滞后1期达到影响峰值，累积效应为-0.1589，随着滞后期数的延长，累积效应逐渐减弱并在第6期后收敛于0；而对于一个标准差考虑非期望产出的土地利用效率（lnte2）冲击，土地稀缺度（lnsca）在滞后1期达到影响峰值，累积效应为-0.019，但影响的持续期较长，到滞后10期才开始收敛于0。

土地稀缺对土地利用效率的冲击影响程度持续下降，但是作用时间存在较大差异。从图2中总结具体脉冲响应情况为：对于1个标准差土地稀缺度（lnsca）冲击，传统土地利用效率（lnte1）在0期时反应最强烈，效应值为-0.017。之后呈现负向的变化趋势，但是从第1期开始呈现正向变化趋势，并从第4期之后收敛于0。而对于1个标准差土地稀缺度（lnsca）冲击，考虑非期望产出土地利用效率（lnte2）产生明显负向影响，仍在0期时达到影响峰值，效应为-0.168，并随着时间的推移逐渐减弱并从第8期开始收敛于0。

3.4 城市土地利用效率与土地稀缺度的预测方差分解

为了测度变量之间因果关系的强弱，接下来采用方差分解来对lnte1与lnsca、lnte2与lnsca两组变量不同预测期限的均方误差进行分解。利用面板模型的方差分解，进一步说明影响因素的大小，结果如下：

（1）土地利用效率冲击对土地稀缺度尚无明显影响。传统土地利用效率、考虑非期望产出的土地利用效率对土地稀缺度的预测方差贡献度分别为0%～15.6%、0%～2.9%。由于本文在测算土地利用效率时，选择的是产出导向，关注的是在不增加投入的条件下，要达到技术有效各项产出应该增加的程度（传统土地利用效率中笼统指产出最大化；在考虑非期望产出的土地利用效率指期望产出最大，非期望产出最小）。也就是说，无论当传统土地利用效率还是考虑非期望产出的土地利用效率改善或者恶化时，表示的是产出量的变动而非投入量的变动。而与土地稀缺度指标中人均建设用地规模相关的建成区面积是效率测算中的投入指标，因而并不会对土地稀缺度的变化产生影响。结合长三角地区城市发展的实际情况来看，经济的快速发展已经消耗了大量的资源，因而通过增加资源投入的方式增加产出，提高土地利用效率已经不是最佳途径。因此，无论是传统土地利用效率（lnte1）还是考虑非期望产出的土地利用效率（lnte2），对土地稀缺的缓解作用均尚不明显。

（2）土地稀缺度对考虑非期望产出的土地利用效率产生显著影响，而传统土地利用效率对土地稀缺度的影响仍不显著，这一结果明显区别于土地利用效率对稀缺度的影响。土地稀缺度对考虑非期望产出的土地利用效率的影响程度在持续下降，但仍保持50.8%～62.1%，而对传统土地利用效率预测方差的贡献度仅为1.4%～1.7%。当前长三角地区人均建设用地规模的不断扩大，建设用地“后备资源”储量不足，不能再简单通过增加投入的方式提高产出。传统土地利用效率并没有考虑工业生产活动中伴生的污染物等具有负面效应的产出项，测算出的土地利用效率整体偏高，面对土地稀缺度冲击所产生的负向效应也不明显。而本文测算的考虑非期望产出的土地利用效率，剔除了土地利用中产生废弃物的负面影响，土地利用效率值比传统土地利用效率值低。当土地稀缺程度发生变化时，考虑非期望产出的土地利用效率会产生更为敏感的变化。该结果也对未来长三角地区城市化土地利用过程中“废弃物”的治理有着警示作用，倘若无视土地利用环境的改善，对污染物的治理力度不够有力，那么土地利用效率负向变化程度会越明显，这对于城市建设是非常不利的。

4 主要结论与政策建议

4.1 主要结论

本文以长三角地区26个城市为研究对象，以城市土地利用效率和土地稀缺度的关系为切入点，采用多种经济计量分析工具分别探究了传统土地利用效率、考虑非期望产出的土地利用效率与土地稀缺度的交互影响，结果表明：

（1）研究时段内，长三角地区城市土地利用效率对土地稀缺具有负向冲击累积效应，但土地利用效率对土地稀缺的预测方差贡献度低于20%，表明城市土地利用效率提升尚未明显缓解土地稀缺。这意味着城市发展过程中，如果建设用地规模扩张得不到有效控制，纵使土地利用效率改善，也无益于土地稀缺的缓解。

（2）长三角地区城市土地稀缺对考虑非期望产出的土地利用效率带来长期显著负向冲击，土地稀缺对考虑非期望产出的土地利用效率的预测方差贡献度超过50%，表明城市土地稀缺增加对于考虑非期望产出的土地利用效率具有负向作用。当剔除土地利用中的非期望产出后，土地利用效率出现明显的下降趋势，土地稀缺度对其造成的影响程度也更高。这与“土地稀缺度是考虑非期望产出的土地利用效率的Granger原因”的结果是一致的，也意味着随着城市土地稀缺程度的加剧，土地利用效率改善将显得更为迫切。

（3）土地稀缺对传统土地利用效率短期内产生负向冲击，长期发展会逐渐转变为正向影响，但土地稀缺对传统土地利用效率预测方差贡献度仅为1.4%～1.7%，表明城市土地稀缺增加对于传统土地利用效率的冲击并不明显。

4.2 政策建议

本文以土地资源效率与稀缺的关系为研究对象，证明了土地稀缺提升的确会在某种程度上造成考虑非期望产出的土地利用效率的下降。同时需要注意的是，土地利用效率的提升并不会显著缓解土地稀缺，或者说短期内改变不了土地稀缺程度继续加重的现实，再一次验证了资源效率的提升并不一定会缓解资源稀缺状况。因此长三角城市土地利用过程中，随着城市土地稀缺度不断增加，提高土地利用强度，整治、盘活闲置土地，同时重视对土地利用过程中环境污染“副产品”的管制，严格把控污染物排放量和排放水平。总而言之，尽管长三角地区经济发达程度较高，但今后经济发展不能继续以牺牲环境为代价，只有严格土地管理，才能为资源永续利用提供更大的可能性。