用户侧热电联产机组基于优化热点域的综合需求响应模型

张志昌，冯蒙霜， 惠锦，管笠，齐保振，蔡晖，徐海华，朱星阳，霍沫霖

(1.国网江苏省电力有限公司苏州供电分公司, 江苏省苏州市 215000；2.国网(苏州)城市能源研究院有限责任公司，江苏省苏州市 215000)

0 引 言

热电联产机组(combined heat and power units, CHP)能够利用汽轮发电机做过功的蒸汽对工业或居民用户供热，蒸汽没有冷源损失，热效率较高[1]。根据蒸汽利用方式，可将CHP分为直接利用汽轮机排气供热的背压式机组以及从汽轮机蒸汽循环中抽气供热的抽凝式机组[2]。其中抽凝式机组通过调整抽气量的大小，能够实现发电出力与供热出力在一定范围内的灵活调节。

随着综合能源系统的发展，用户侧的CHP机组不断普及。用户侧CHP机组通过热电耦合，为供能系统提供了大量灵活性。在多种能源相互耦合的背景下，传统的需求响应模式需要向综合需求响应转变[3]。用户侧的CHP机组可以在一定范围内实现供热和供电的灵活调节，满足用户的电能和热能的需求。配置有CHP机组的用户，可以通过调节CHP的电、热出力，改变自身对于外界电能和热能的需求，响应和参与到综合需求响应中。因此，考虑用户侧CHP的需求响应优化模型，可以实现电力系统与热力系统的联合调度，从而实现综合需求响应。提出准确、高效、简洁的用户侧CHP需求响应模型，对于实现综合需求响应具有很大意义。

目前，绝大多数优化模型中CHP成本函数的形式为发电量和发热量的二元二次函数[4]。在综合需求响应中使用非线性的CHP成本函数，将使得模型难以采用商用优化软件求解。现有文献中对CHP成本函数的处理方法各有不同，主要可以分为直接计算法和可行域顶点线性组合近似法。

直接计算法是指构造非线性优化模型，直接求解二次规划模型。早期文献[5-7]对优化求解过程进行了较深入的探讨，文献[5]提出了基于牛顿拉弗逊法求解背压机组优化运行的算法。目前，随着计算软件的发展，部分文献直接利用商业软件求解[7-8]，文献[9-10]在研究存在储热情况下CHP的优化问题，直接运用CPLEX软件对二元二次成本函数进行优化求解。大量智能算法被用于求解包含二元二次成本函数的优化模型[11-15]，文献[11]提出加强免疫算法，用来求解考虑了混合燃料以及排放约束等条件下CHP机组在电力市场中优化运行的调度问题，实现了在复杂约束下CHP机组优化运行的求解。直接考虑CHP二次成本的模型的优点在于能够精确刻画CHP的运行成本，模型简单；但其不足在于二次成本函数给优化求解引入了更多非线性因素，求解速度慢。当采用人工智能算法求解时，又有可能出现所得解并非全局最优，求解过程不收敛等问题。

另一部分文献则采用CHP电热运行可行域顶点的线性组合来表示实际优化运行点的电热出力大小和成本[16-18]，可以使模型转变为一个线性优化问题。文献[17]针对CHP在变化电价的电力市场中成本优化问题，提出了一种运行状态的快速确定方法，快速确定优化运行点和做出调整策略。文献[18]则将这一方法运用到了非凸的CHP运行区间内，结合CHP出力区间的形状，对不同顶点的线性组合系数加以限制，使得非凸运行区间的CHP优化运行也可以使用可行域顶点的线性组合模型来表示出力大小和成本。相较于直接考虑二次成本函数，顶点线性组合法消除了CHP成本计算中的非线性因素，进而使模型变为线性规划问题。但对于某个运行点而言，CHP机组4个运行点线性组合的系数不是唯一的，因此会给优化中带来较多的自由度，降低求解的效率。特别是对于包含机组开停机状态0-1变量的机组组合问题而言，更是增加了求解的复杂性。

本文以综合需求响应为实际背景，在CHP电热运行可行域顶点线性组合模型的基础上，对CHP的运行原理和其在综合需求响应中的作用进行探讨，揭示CHP相对于发电机组与燃煤锅炉组成的电热解耦的“等效CHP”具有成本优势的区域。将经济性优于“等效CHP”对应的运行区域识别为“优化热点域”，建模为具有3个顶点的三角形可行域，缩小综合需求响应模型的优化空间，提升优化效率。最后在Lingo环境下，将本文提出的模型与传统模型进行对比。

1 CHP在多能源综合系统中的特点分析

抽凝式CHP能够通过调节抽气蒸汽比例，在汽轮机主蒸汽量不变的情况下调节发电和供热比率。本节从多能源互补系统的角度，分析抽凝式燃煤CHP的供热供电灵活特性以及在其灵活调节范围内各运行点的成本优势大小。如无特别说明，下文中CHP指抽凝式燃煤热电联产机组。

1.1 CHP的灵活优势特点

目前，多数文献均将CHP的电热出力运行区间表述为一个凸四边形的形式，CHP典型出力区间各边界所对应的CHP运行物理约束如图1所示[19]。由图1可以看出，相对于“以热定电”的背压式热电机组而言，抽凝式机组具有很大的灵活性优势，即能够适应不同供热供电比例。

为了说明CHP运行的成本优势，本文将CHP机组与发电供热解耦的系统进行对比。分别引入“常规发电机组+燃煤锅炉”以及“常规发电机组+电锅炉”2种“等效CHP”。图2中分别对比了CHP机组(300 MW)与常规发电机组(300 MW)+电锅炉 (50 MW)，以及常规发电机组(300 MW)+燃煤锅炉(200 MW)的运行区间。可见，采用常规发电机组与燃煤锅炉或电锅炉联合运行的方式，基本能够覆盖CHP的运行区间，即能够实现与CHP相同的供电供热能力。基于此，1.2节将比较相同灵活性下CHP相对于上述2种“等效CHP”的运行成本优势。

图1 CHP运行区间Fig.1 Operating region of CHP

图2 CHP与“等效CHP”运行区间Fig.2 Operating region of CHP and virtual CHP

1.2 CHP的成本优势特点

CHP能够利用发电后的蒸汽中余热进行供热，提高了能量利用率[19]。理论上，在供应同等大小的电热负荷时，CHP的运行成本将会比“等效CHP”更低。定义CHP成本优势ΔC为单位调度时段内等量电热出力情况下，系统内“常规机组+燃煤锅炉”这一组合的供应负荷费用与CHP的运行费用的差值。

ΔC=Cgen(P)+Cboiler(Q)-CCHP(P,Q)

(1)

式中：ΔC单位取决于CHP成本函数与“发电机组+燃煤锅炉”成本函数的单位，通常用单位调度时段的煤耗(单位：t)或煤耗对应的经济成本(单位：美元)表示；Cgen(P) 为发电机组的成本函数；Cboiler(Q) 为燃煤锅炉的成本函数；CCHP(P,Q)为CHP的成本函数；P和Q分别代表电功率和热功率数值。对3种设备而言，成本与热电功率并无严格的线性或二次对应关系，因此成本函数实际上并不是严格的线性函数或二次函数。但在实际工程算例中，往往采用线性函数或二次函数对实际成本函数进行近似，其近似效果对工程计算而言已足够精确。

根据文献[4]中的机组数据得到：

Cgen(P)=50P

CCHP(P,Q)=1 250+36P+0.043 5P2+

0.6Q+0.027Q2+0.011PQ

Cboiler=23.4Q

根据以上模型，ΔC在CHP出力区间上的变化情况如图3所示。

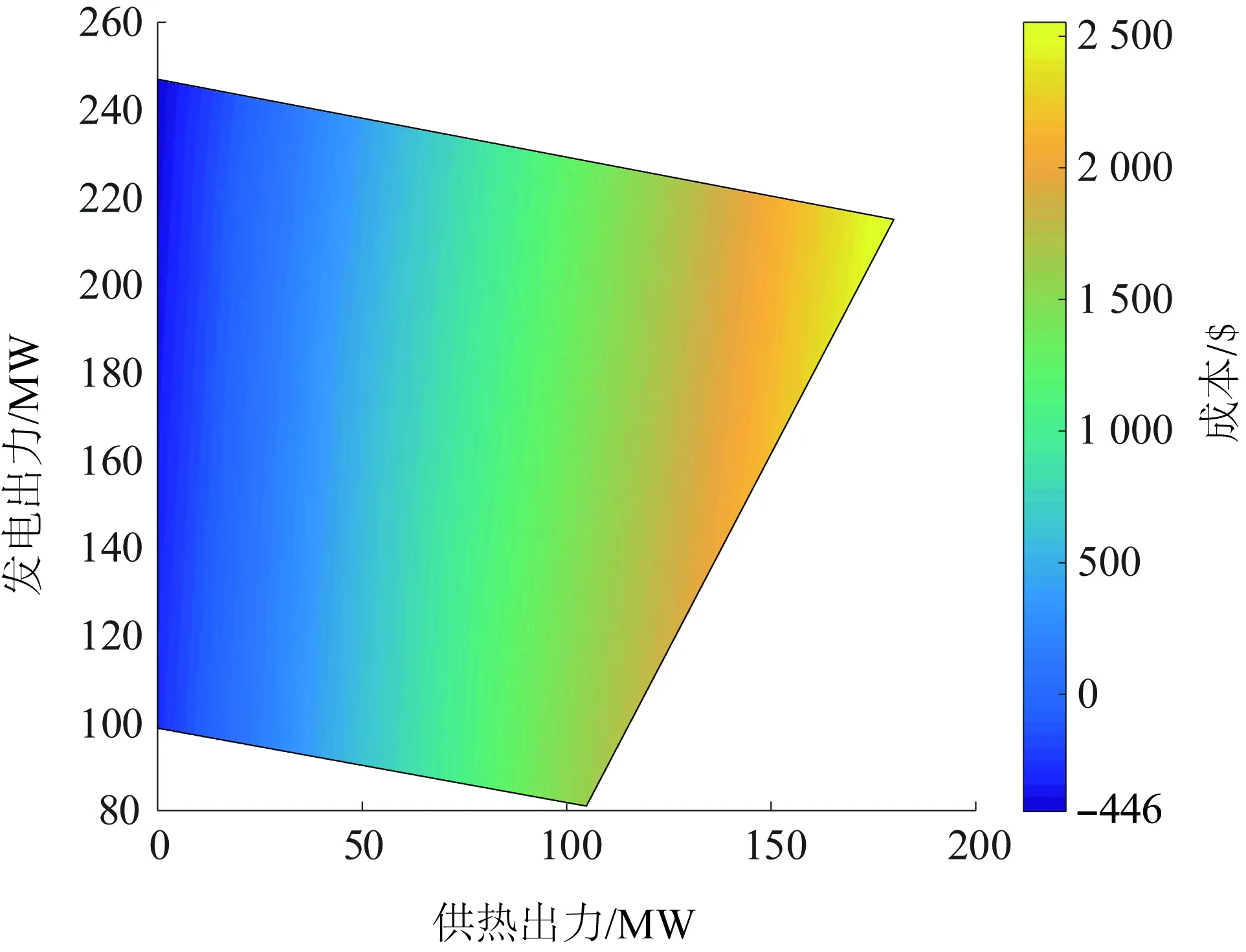
图3 CHP成本优势Fig.3 Cost advantage of CHP

图3所示结果表明，由于CHP充分利用蒸汽做功后的热能，使CHP能够在供热量较高的时候具有较大的成本优势。CHP热量供应出力越多，对蒸汽余热利用越充分，其成本优势越大。而当CHP在仅是发电状态下，其并没有充分对蒸汽余热进行利用，成本优势骤降，甚至其发电成本可能会比大容量先进常规燃煤发电机组成本更高。对于“常规机组+电锅炉”这一等效CHP组合，由于高品质的电能被直接等量转化为低品质的热能，其能量利用效率和经济性与CHP相比必然更低。

1.3 CHP不同运行状态的成本特征

对成本优势的理论分析和实例验证表明，CHP在供热量较大的状态下工作效率较高，而在低供热甚至纯发电状态的时候，其运行效率低于大容量先进常规燃煤发电机组。根据CHP机组的成本优势分析可知，使其工作于较大供热量下的状态可以取得更高的效率，提升运行经济性。

在综合需求响应中，若以多能源系统运行成本最低作为优化目标，根据CHP的运行特点，显然CHP会在其他约束都满足的条件下，尽量靠近最大抽汽工况的约束边界出力，从而获得更好的经济效益。这一点可在文献[20-22]等得到理论分析与实际算例的验证。

2 综合需求响应中基于“优化热点域”的CHP调度模型

2.1 “优化热点域”概念

如第1节所述，CHP在不同工况下的运行成本有较大差异。这种差异可以反映在CHP的可行域建模中，从而获得更加高效的建模方法。传统的可行域顶点线性组合近似法考虑了CHP全部运行可行域进行优化计算，并未考虑CHP在供热供电时运行成本的特点。实际上CHP的实际运行点绝大多数集中在最大抽汽约束工况线的附近，即电热出力区域的右侧。对于运行区间的左下角，即供热供电出力较低的区域，其供热与供电成本不占优势，往往不符合运行优化模型的最优性条件，因此可以判定CHP的最优运行点几乎不会出现在电热区域的左下角。

根据上述判断，本文提出对传统模型的改进策略：即基于CHP成本优势最大的区域，构造“优化热点域”，以表征CHP运行点服从最优性条件的区域。“优化热点域”完全包含在CHP的电热出力可行域内，但只覆盖在实际优化过程中CHP出力点最可能出现的区域，不再考虑出力点几乎不可能出现的区域，进而在不漏掉模型最优解的前提下缩小了优化寻优空间。

2.2 “优化热点域”的确定原则

CHP“优化热点域”具体的确定原则包括：灵活运行原则、成本优势原则以及简单原则。

(1)灵活运行原则。CHP具有灵活运行的优势，在确定优化热点域的过程中，需要尽量体现出CHP在供电与供热上的灵活性。一方面，电力系统要求负荷与发电实时平衡，要求CHP的电出力能够具有较大的灵活性；另一方面，热力系统具有较长的平衡时间和储能能力，且热负荷变动没有电负荷大，对CHP灵活性要求并不高，但CHP往往是多能源系统中热负荷的主要承担者。因此CHP的“优化热点域”需要保证发电出力范围跨度大，同时热出力范围尽可能满足机组相应承担的热负荷波动范围。

(2)成本优势原则。多能源系统的运行需要遵循经济的原则，大部分优化问题中的目标函数均为系统总运行成本最低。在确定CHP“优化热点域”时，需要考虑CHP的运行成本，应当尽量包括所有成本优势大的区域，使得最终的求解结果具有较好的经济性。

(3)简单原则。从原来的电热出力区间中提取出来的“优化热点域”，其表达形式应比原有可行域更加简洁，如在四边形的出力区间内提取出三角形的“优化热点域”，在非凸的电热运行区间提取具有凸性的优化热点域。

2.3 “优化热点域”的建模方法

按照所提出的3个选取原则，需要保证选取的可行域具有较大的运行灵活性和较高的经济性，同时应该较为简单，易于数学表示。最大抽汽工况约束线附近的区域，其发电量灵活调节范围与CHP整体出力区间的调节范围接近，同时保持了一定的热出力调整范围，成本优势最大。故首先选取最大抽汽约束线上的2个端点(A，B)作为“优化热点域”2个顶点，从而保证可行域的经济性。遵从简单原则，选取的“优化热点域”是由3个顶点确定的三角形区域，因此还需要再确定1个顶点。为保留足够的灵活运行空间，尽可能避免实际出力点出现在优化热点域之外，同时实现对电热运行出力区间的简化，可以选用电热运行区间左侧某个顶点作为“优化热点域”的第3个顶点。

对于凸性的电热出力区间，选取与左上方最大凝气工况线的另一个端点C点所构成的三角形区域，因其相比于左下方D点，所构造的三角形区域能够更好覆盖成本优势大的区域。此时CHP优化区间变为了图4中右上方的三角形区域，即“优化热点域”。

图4 CHP电热出力区域的划分 (凸运行区间)Fig.4 Division of CHP operating region (Convex operation region)

对于非凸的运行区间，考虑到CHP承担热负荷为零时经济性较差，因此选取左上方热出力较大的顶点作为优化热点域的第3个顶点，如图5所示。

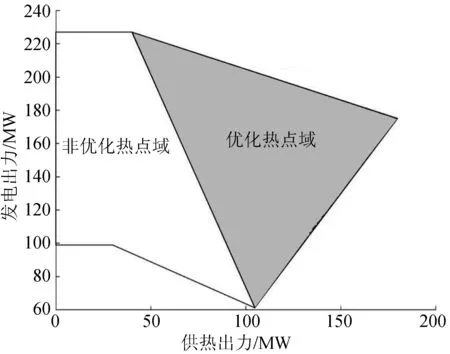
图5 CHP电热出力区域划分(非凸运行区间)Fig.5 Division of CHP operating region (Non-convex operation region)

确定优化热点域后，将CHP的电热出力和成本用数学公式表述如下：

(2)

(3)

(4)

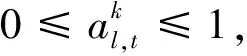
(5)

(6)

式中：T表示热电综合调度的时间跨度,h；Nc代表CHP的机组数量。

2.4 基于CHP“优化热点域”的综合需求响应模型

基于本文提出的CHP“优化热点域”模型，可建立综合需求响应基本模型。其优化目标为系统总运行成本最低：

(7)

(8)

(9)

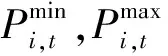
(10)

(11)

对于第l台CHP机组在第t小时内的发电量与供热量Pl,t,Ql,t的约束条件为式(2)—(6)。

上述模型仅为考虑多能系统成本最优的综合需求响应模型，此外还可进一步考虑更多复杂的约束。

2.5 “优化热点域”与传统线性化算法复杂度对比

本文提出的“优化热点域”模型与传统模型相比，减少了综合需求响应模型中优化变量个数以及约束个数。具体分析如下文所述。

对于每个调度时段，传统模型需要4个顶点的线性组合系数变量来确定，约束包括出力区间的4条边界约束以及顶点线性组合系数的相关约束(每个线性组合系数范围在0与1之间，总和为1)，而优化热点域需要3个顶点线性组合变量，3条边界约束及线性组合系数变量的相关约束。

对于非凸的电热出力区域[2,18]，传统模型需要先对非凸区域进行分割得到2个凸性区域，每个凸性区域需要的变量和约束个数与上文相同，另外还需要用2个0-1变量表征出力点落在哪块凸性区域，以及这2个0-1变量和为1的约束。优化热点域所需变量和约束则仍与上文凸性区间的处理相同。

对于包含CHP的综合需求响应问题的每个调节时段，2种方法在2种情况下(CHP凸性出力区间，CHP非凸出力区间)计算CHP出力点时，涉及的变量和约束数量对比如表1所示。

表1 模型变量数与约束数量对比Table 1 Comparison of the numbers of variables and constraints among different models

在CHP运行区间为凸区域的情况下，优化热点域的建模方法将传统方法的4个变量缩减为3个，9条约束减少为7条。而在非凸运行区间下，传统方法需要10个变量和19条约束，优化热点域方法只需3个变量和7条约束。在这种情况下，优化热点域方法在处理具有非凸运行区间的CHP机组时具有很大的优势，对于包含较多时段的综合需求响应模型，采用基于优化热点域的方法，能为整个优化模型节省大量变量及约束条件。

3 算例分析

3.1 基础数据

参考文献[2]中的算例系统，系统中有2台常规机组(G1和G2，最大出力为300 MW)和2台热电联产机组(CHP-1，CHP-2)，风电机组W1。CHP-1和CHP-2的运行边界点如表2所示

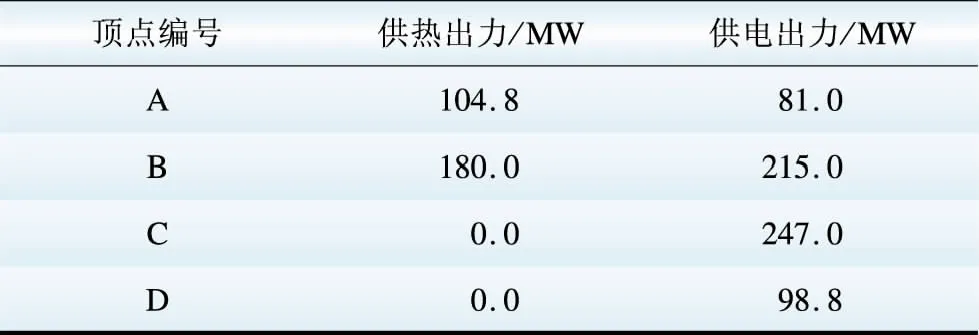
表2 CHP运行可行域边界点Table 2 Parameters of operation region of CHP

根据文献[9],常规机组的成本函数为

Cgen=0.000 171P2+0.270 5P+11.537

(12)

热电机组的成本函数为

CCHP=0.000 072(P+0.17Q)2+
0.229 2(P+0.17Q)+14.618

(13)

燃煤锅炉的成本函数为

Cboiler=0.15Q

(14)

式中P与Q分别代表电出力和热出力，MW。文献[9]中机组运行成本以煤耗计算，单位t。

构造2个供热区域，第一个供热区域由CHP-1与1台燃煤锅炉作为热源；第二个供热区域由CHP-2作为唯一热源。供热区域二的热负荷为区域一热负荷的3/4。电热负荷曲线及风电出力曲线如图6和图7所示。

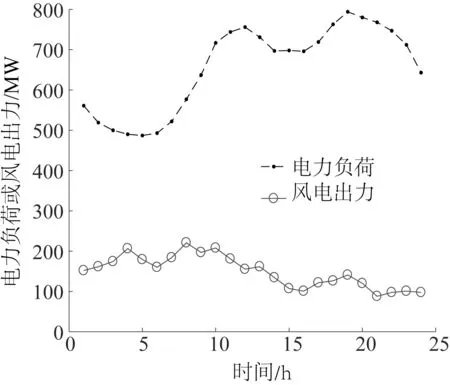
图6 电力负荷与风电出力曲线Fig.6 Profiles of system electric load and available wind power of a typical day

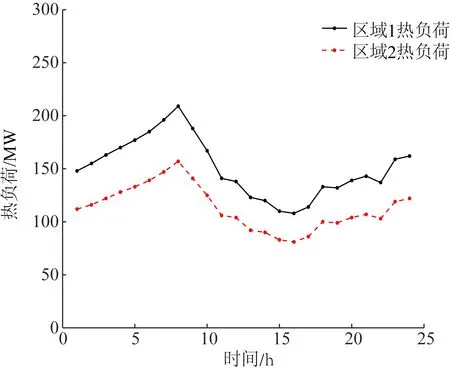
图7 系统热负荷曲线Fig.7 Profiles of system heat load

本算例中将3种CHP成本建模方法进行对比，即直接代入二次成本曲线进行计算(方法一)，所有可行域顶点的线性组合法(方法二)以及改进后的“优化热点域”(方法三)计算模型，分别对比其求解速度以及迭代次数。取单位调度时长为1 h,调度周期为 7 d，进行机组综合优化；为简化计算，约束条件主要是电热负荷平衡约束、机组出力范围约束。采用Lingo软件进行求解。

3.2 算例结果

3种方法依次轮流进行了10次运算，运算求解速度及迭代次数如表3所示。

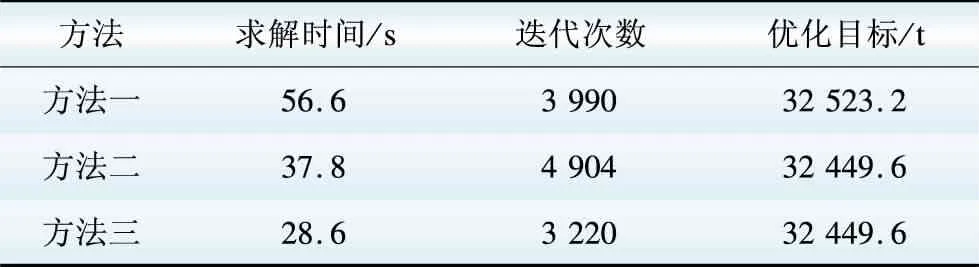
表3 3种方法优化结果对比Table 3 Comparison of the optimization results using different models

3种方法对CHP各时段出力的优化调度方案几乎完全相同，其总成本数值有微小偏差的原因在于方案二与方案三的成本函数是方案一成本函数的近似。

3种方法的优化调度中，CHP-1和CHP-2运行出力点数据的分布如图8(a)和图8(b)所示。

图8 CHP-1与CHP-2运行点优化结果Fig.8 Dispatch result of output power and heat of CHP

3.3 结果分析

3种方法的计算结果中，CHP的运行点总是靠近右侧供热出力较多的区域；加之右侧区域相较于左侧区域，CHP运行的成本优势大，因此，CHP在多能系统中的出力点总是靠近于顶点B，即电热出力均较高的“优化热点域”。改进的计算模型注意到CHP这一运行特点，相较于传统方法对整个区域的建模，改进的模型只对右侧区域分配计算资源，采用了3个顶点组合成的三角形区域构造更具有实际优化价值的“优化热点域”。

相较于传统的全区域算法，由于计算区域及顶点数的减少，其运算速度将会更快，与方法一(直接代入二次成本曲线求解)比较，求解时间下降49.5%，迭代次数下降19.3%；与方法二(可行域全顶点的线性组合法)比较，求解时间下降24.3%，迭代次数下降34.3%。

3.4 大规模优化算例

对基础算例的机组个数和调度时长进行扩展，以构造更大规模的算例。

表4 算例中机组类型及数量Table 4 Amount of different types of units used in the case study

将CHP和发电机组的数量各增至6台，单台机组容量不变。并对3台CHP机组的左侧运行区间进行改动，引入非凸性。热电负荷与风电出力随机组数量的增加而扩大相应倍数。单位调度时长仍为1 h，但优化周期从7 d延长为30 d。分别用3种方法，以总运行成本最小为目标进行优化调度。

随着机组数量的增多和运算量的增大，直接代入二元二次成本函数引入了大量非线性，使得商业软件求解变得极为困难，在20 min内仍无法得出全局最优解。可行域全顶点的线性组合法花费18 min找到全局最优解，而优化热点域的计算模型只需要 12 min。可见，随着机组数量和优化时间的增加，以及非凸运行区间的CHP机组引入，优化热点域的计算模型相对于传统的2种方法，其优势更明显。

4 结 论

在用户侧CHP的建模中，本文根据CHP的运行原理，揭示了CHP“成本优势”在电热出力可行域上的分布；在多能源综合系统背景下，从用户侧CHP机组的原可行域中提取出对综合需求响应更具有优化价值和意义的“优化域”。在用户侧CHP机组的综合需求响应模型中，应用“优化域”概念，对传统的可行域全顶点的线性组合法进行了改进，提出了基于优化热点域的CHP机组参与综合需求响应模型。

算例表明，这一改进计算模型相对于传统方法，在获得综合需求响应最优解的过程中，能够降低运算时间和迭代次数。若系统中引入了储热、热泵等更多种类的供热装置，此时CHP的“优化热点域”可能将会相应改变。如何将这些因素与成本优化综合考虑，提出在综合需求响应中更具有普适性的CHP“优化热点域”的模型，将是下一步研究的方向。