基于深度森林算法的电力系统短期负荷预测
陈吕鹏, 殷林飞, 余涛, 王克英
(1.华南理工大学电力学院,广州市 510640;2.广东省绿色能源技术重点实验室,广州市 510640;3.广西大学电气工程学院,南宁市 530004)
0 引 言
作为电力调度部门重要的日常工作之一,负荷预测可以指导电力生产部门经济地制定发电计划和确定电力系统运行方式。精准的负荷预测有利于提高电力系统的安全稳定性,降低发电成本,提高电力企业的整体效益[1]。长久以来,国内外学者对负荷预测的理论和方法进行了大量研究。其中,传统的时间序列法作为经典负荷预测方法的代表,具有预测模型简单,预测所需数据量不大的优点[2]。但由于该方法强调时间因素在预测当中所起的作用,而淡化其他外界因素影响,导致预测误差较大[1]。
20世纪80年代以来,随着计算机与人工智能技术发展,许多以机器学习为基础的智能预测算法相继问世。同时,为了提高电力系统负荷预测的精准度,电力系统专家和学者开始尝试将智能预测算法运用到电力系统负荷预测之中[3-5],并逐步提出现代负荷预测的理论。现代负荷预测理论主要有:灰色数学理论、专家系统方法、模糊负荷预测以及人工神经网络等[1]。其中,人工神经网络(artificial neural network, ANN)及其优化算法被广泛运用于各种预测之中。ANN具有自学习以及联想记忆的能力,能够充分逼近复杂的非线性关系,具有鲁棒性和容错性[6]。因此,对于电力系统负荷预测这类非线性问题,ANN能有效地进行求解[6-9]。但ANN存在训练速度慢,须人为设置和调整大量超参数的不足。同时,ANN易陷入局部最优解甚至无法收敛到最优解,导致预测失准[7]。随着深度学习(deep learning)的概念被机器学习专家和学者提出[10-11],深度神经网络(deep neural network, DNN)及其优化算法开始逐步成为目前深度学习的代表[12]。DNN具有深度学习理论中表征学习的能力[13],可以利用更少的超参数处理复杂模型[14]。同时,DNN采用了预训练的方法缓解了算法易陷入局部最优的问题[15]。因此,DNN同样具备负荷预测的能力,也被应用到了负荷预测领域[14]。但是,DNN依然存在训练速度慢[16],训练效果取决于人为对超参数的设置和调整的不足[7]。
国内南京大学机器学习与数据挖掘研究所(learning and mining from data, LAMDA)的周志华教授提出了深度森林算法(deep forest),也称作多粒度级联森林算法(multi-grained cascade forest, gcForest)。作为一种基于决策树的集成分类算法,深度森林算法的试验预测能力可与深度神经网络算法相媲美[17]。同时,深度森林算法只需设置少量超参数,且在训练过程中不需要人为调整大量超参数[17]。试验表明,深度森林算法默认的超参数设置适用于处理不同领域的不同任务。即使不对超参数进行调整,也能取得有效的预测效果[17]。另外,作为一种基于决策树的方法,深度森林算法从结构上适合于并行训练,具有表征学习的能力,且在理论分析方面也比深度神经网络容易[17]。本文将深度森林分类算法尝试性地引入电力系统短期负荷预测领域,验证深度森林分类算法的预测能力,并探究其在电力系统短期负荷预测的可行性。
1 短期负荷预测
短期负荷预测是电力系统负荷预测的重要组成部分,主要对未来某日内每个时刻的负荷量进行合理的预测[1]。精准的短期负荷预测对于电力调度部门的经济调度、控制机组调配以及当前正在发展的电力市场都具有极其重要的意义[18]。
影响短期负荷预测精确度的因素主要有天气突变、季节变化、调度计划、突发事故以及大型社会活动等。因此,短期负荷预测具有随机性和不确定性[19]。但负荷在随机变化过程之中,仍然在年、月、星期和日等不同期限上具有明显的周期性。因此,短期负荷变化综合表现为在时间序列上的非平稳随机过程[20]。
在进行电力系统短期负荷预测之前,应选择具有代表性和影响度高的历史数据资料作为预测依据。电力系统短期负荷预测通常采用以下数据进行预测:(1)历史负荷数据;(2)日期类型数据;(3)天气情况数据等。
精准负荷预测的核心在于获取真实可靠的历史数据和建立有效的负荷预测模型。随着电力系统信息管理系统的建立以及气象数据预测精确度的提高,精确获取电力系统历史负荷数据以及未来天气情况已不再困难。因此,建立有效的负荷预测模型成为提高电力系统负荷预测精准度的关键[20]。
2 深度森林算法分析
深度森林算法是在深度学习理论以及深度神经网络的启发下,以随机森林算法(random forest, RF)为基础的一种有监督机器集成学习算法。作为一种具有一定深度的基于决策树的预测算法,深度森林算法将预测过程分为2个阶段:多粒度扫描阶段(multi-grained scanning)和级联森林阶段(cascade forest)。以下将依次对随机森林算法、多粒度扫描阶段和级联森林阶段进行分析。
2.1 随机森林算法
随机森林算法是重要的机器集成学习算法之一,其基础是Breiman在1996年提出的Bagging集成算法[21]和Ho在1998年提出的随机子空间方法[22]。随机森林模型是一个由一组决策树分类器{h(X,Θk),k=1,…,N}组成的集成分类模型。其中参数Θk是与第k棵决策树独立同分布的随机向量,表示该棵决策树的生长过程;X为待分类样本。随机森林算法的具体分类过程如图1所示。
当向随机森林模型输入待分类样本X后,样本X
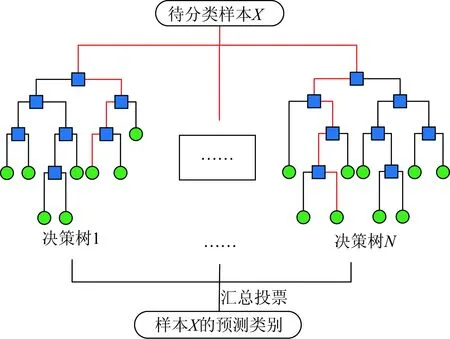
图1 随机森林分类过程Fig.1 Classification procedure of random forest
将会进入所有经过训练产生的决策树,从而进行分类。各棵决策树将依据样本的特征属性独自确定样本X的类型。当所有决策树得出各自的分类结果之后,随机森林模型进行汇总投票。获得票数最高的类别将被确定为样本X的预测分类类别。因此,随机森林的分类决策如式(1)所示[23]:
(1)
式中:H(x)为随机森林分类决策结果;hi为第i个决策树分类模型;Y为目标变量;I为度量函数;N为决策树数量。
式(1)体现了随机森林算法的多数投票决策方式。作为一种基于决策树的集成算法,随机森林模型在构造的过程中,构造不同的训练集对各决策树进行训练,从而增加了各分类器之间的差异程度,并使随机森林算法具有超越单个决策树算法的分类效果。为体现随机森林模型的随机性,训练集的构造包含2个关键过程,如下详述。
2.1.1随机选取样本数据过程
随机森林算法对原始训练数据集进行随机有放回抽样,构造出样本容量大小与原始数据集相一致的子数据集。不同子数据集中的样本可以重复,同1个子数据集中的样本也可以重复。每个子数据集对应产生1棵决策树。
2.1.2随机选取待选特征过程
随机森林模型中每一棵决策树的分裂过程只利用了所有的待选特征中的一部分特征。随机森林算法先从所有的待选特征中随机选取一定数量的特征,之后再通过决策树生成算法[24-26],在随机选取出的特征中选择最优的特征进行分裂。
随机森林模型在构造过程中所体现的随机性和不完整性,解决了单个决策树分类精度不高,易出现过拟合等问题,提高了算法的泛化能力[27]。
深度森林算法中随机森林的决策树一般采用分类回归决策树(classification and regression tree, CART)。CART是由Breiman等人提出的一种典型二叉决策树,能够有效地处理大数据样本,解决非线性分类问题。因此,CART适合解决分类机理不明确的分类问题[26]。
决策树生成算法的核心在于如何选取每个节点上需要进行测试的属性和如何根据不同的数据度量方法对数据纯度进行划分。CART以基尼(Gini)指数作为属性度量标准,Gini指数越小,则划分效果越精确。Gini指数定义如式(2)所示:
(2)
式中:p(i|t)为测试变量t属于类i的概率;c为样本的个数。
当kGini=0时,所有的样例同属于一类。若属性满足一定纯度,决策树生成算法将样本划分在左子树,否则将样本划分到右子树。CART决策树生成算法根据kGini指数最小的原则来选择分裂属性规则。假设训练集C中的属性A将C划分为C1与C2,则给定划分C的kGini指数为
(3)
决策树的生长深度受条件限制,不能无限制生长下去。决策树停止生长的条件如下:(1)节点的数据量小于指定值;(2)Gini指数小于阈值;(3)决策树的深度达到指定值;(4)所有特征已经使用完毕。
2.2 多粒度扫描阶段
对于序列数据样本而言,预测算法有效地处理样本特性,并且把握样本中各个特征的顺序关系,有利于提高预测的精确度[28-29]。为提高深度森林算法中级联森林阶段的预测效果,深度森林算法设置了多粒度扫描阶段来对样本特征进行提取,尽可能地挖掘序列数据特征的顺序关系。深度森林算法中多粒度扫描的示意图如图2所示。
图2中假定存在1个未经多粒度扫描的具有200维特征向量的样本。深度森林算法希望解决二分类问题。其多粒度扫描的具体步骤如下:首先,设置1个50维的向量窗口在原始特征向量上进行滑动取值,步长默认取1,则可获得151个50维向量;然后,将所得的向量分别经2种不同类型的森林模型进行分类处理,分别得到151个2维的分类向量;最后,再将所有分类向量按顺序拼接组成1个604维的特征向量,作为级联森林的输入。

图2 多粒度扫描过程Fig.2 Procedure of multi-grained scanning
图2中仅展示了采用1种大小的取值窗口进行多粒度扫描的过程,而在实际运用深度森林算法时,默认会设置多个不同长度的取值窗口。因此,多粒度扫描过程将对应产生多个不同的多粒度特性向量作为级联森林的输入。因此,最终变换所得的特征矢量将包括更多的特征。
深度森林算法通过采用多粒度扫描过程,对原始特征数据进行加工处理,使特征数据维度得以拓展。经过处理后的深度森林算法具有了处理样本特性之间顺序关系的能力,增强了后续级联森林阶段。
2.3 级联森林阶段
深度森林算法通过设置级联森林阶段,以体现其深度学习的过程。级联森林阶段的每一级都由多个不同类型的森林模型组成。深度森林算法利用级联森林阶段对数据特性逐层进行处理,加强了算法的表征学习能力,有利于提高预测精准度。
在级联森林阶段中,每一级都从上一级获取经处理后的特征信息,并利用特征信息产生出新的特征信息传递至下一级。除第1级直接采用经多粒度扫描处理后的特征向量作为输入之外,随后的每一级都将上一级输出的特征结果向量与原始输入特征向量相拼接作为自身的输入。
深度森林算法中级联森林阶段的示意图如图3所示。图3中,级联森林采用经图2中多粒度扫描过程处理后所得的604维特征向量作为输入。首先,特征向量经过2个不同类型的森林模型分类处理后,得到2个2维类别向量。深度森林理论认为这2个2维类别向量能够有效地反映样本的特性,并将其称为增强特性向量。接着,增强特性向量将与604维的原始特征向量相拼接组成608维的特征向量。然后,将具有增强特征的608维特征向量作为下一级的输入向量。依此方法直至进行到级联森林的最后一级。最后,对最后一级产生的类别向量取平均值,再取其中最大值所对应的类别作为样本的分类结果。
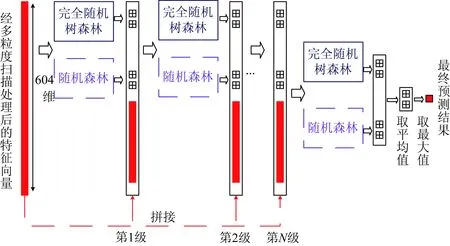
图3 级联森林过程Fig.3 Procedure of cascade forest
在级联森林阶段处理过程中,为了降低过拟合风险,每个森林产生的类别向量均经过k折交叉验证(k-fold cross validation)产生。每个样本都将作为训练数据训练k-1次,从而产生k-1个类别向量。然后,对其取平均值作为下一级的增强特征向量。深度森林算法默认采用3折交叉验证。
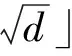
级联森林的级数为深度森林模型的深度,深度森林算法在训练级联森林时可由算法运算自动确定级联森林的级数。每当级联森林训练层数增加一层后,将会采用验证集对级联森林的性能进行测试,如果预测效果没有提升,则停止产生下一层。与深度神经网络算法须人为规定模型复杂程度不同,深度森林算法可以自动确定级联森林的级数,从而调整预测模型的复杂程度。因此,深度森林算法可以适用于不同规模的训练数据,而不局限于大数据集。
2.4 深度森林算法流程
深度森林算法的具体实现步骤如下详述。
(1)对预测所需数据进行预处理。剔除无效数据,并对缺失数据利用线性插值法进行填补。依据预测算法的需要,划分出训练样本集。
(2)利用训练样本集对深度森林算法进行训练。按照深度森林算法的超参数设置,对多粒度扫描阶段和级联森林阶段中的森林模型进行构造,确定级联森林的级数。
(3)利用预测样本的特征数据进行预测。预测样本的特征数据将依次进行多粒度扫描阶段以及级联森林阶段处理。深度森林算法将汇总级联森林的输出结果,得出预测分类结果。
整体预测过程及整体深度森林算法的实现流程如图4、5所示。
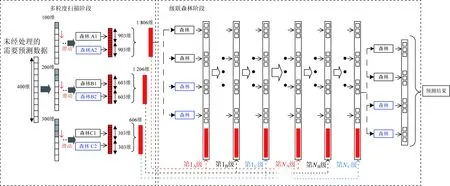
图4 深度森林整体预测过程Fig.4 Forecasting procedure of deep forest
3 预测结果
本文选取了某地区2012年1月1日—2015 年1月10日的电力负荷值(每15 min采样1次,每日96个时刻)、气象因素数据(日最高温度、日最低温度、日平均温度、日相对湿度以及日降雨量)以及日期类型数据(工作日为0,周末为1)对电力系统短期负荷进行了预测,所选数据均来自第九届“中国电机工程学会杯”全国大学生电工数学建模竞赛所提供的标准数据集[31]。取2012年1月1日至2015年1月9日的数据作为历史数据,对深度森林预测模型进行了训练,并分别利用了前21天以及前40天的历史数据预测2015年1月10日当天的负荷量。为评估深度森林算法在短期负荷预测上的能力,本文选取了BP神经网络(back propagation neural network)[32]、随机森林算法(random forest, RF)[33]、袋装分类算法(bagging algorithm)[21]、梯度提升分类算法(gradient boosting algorithm)[34]、k最邻近分类算法(k-nearest neighbor algorithm)[35]5种算法进行负荷预测,并将预测效果与深度森林算法预测效果进行了比较分析。本文预测算法程序均基于MATLAB语言和Python语言编程,仿真环境为MATLAB R2017a 及Python 2.7。
3.1 样本数据及处理
按照深度森林算法的步骤,首先须对数据进行预处理。目前针对负荷预处理的方法有很多,如数据横向比较法、数据纵向比较法以及插值法等。本文中采用数据纵向比较法对原始数据进行预处理。其次,根据基于深度森林算法的周期性负荷预测模型的需要,划分出训练样本集。取连续N天的负荷数据、气象因素数据以及日期类型数据作为训练输入数据,次日的实际负荷数据作为训练输出。
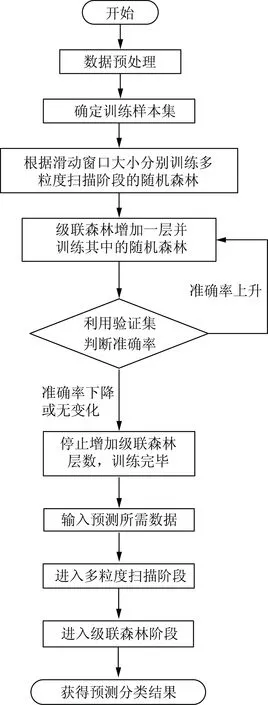
图5 深度森林算法流程Fig.5 Flow chart of deep forest algorithm
以利用前21天的数据进行电力系统短期负荷预测为例。取2012年1月1日—2012年1月21日连续21天的历史负荷、气象数据及日期类型数据作为训练输入,2012年1月22日的实际负荷量作为训练输出,并将此作为训练集中第1个训练样本。直至取到2014年12月19日—2015年1月8日连续21天的历史负荷、气象数据以及日期类型数据作为训练输入,2015年1月9日的实际负荷量作为训练输出,并将此作为训练集中最后1个训练样本。
3.2 预测模型
电力负荷变化具有周期特性。因此,构造了一种基于深度森林算法的周期性负荷预测模型,如图6所示(文中N先后取21和40)。
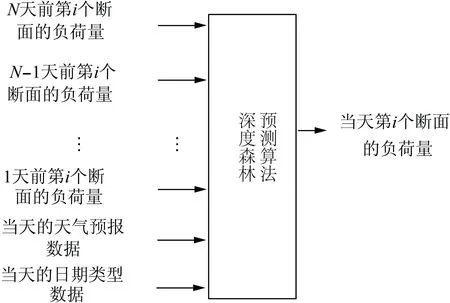
图6 基于深度森林算法的周期性负荷的预测模型Fig.6 Forecasting model of periodic load based on deep forest
3.3 算法性能评估指标
本文各算法预测性能采用平均绝对百分比误差指标(mean absolute percentage error, MAPE)和最大相对误差进行评估。MAPE和最大相对误差的计算公式如式(4)、(5)所示:
(4)
(5)
总共统计96个时刻的绝对百分比误差,分别取平均值δ和最大值ε对算法性能进行评估。δ、ε越小说明算法的预测效果越精确。
3.4 深度森林算法中超参数的设置
文献[17]中介绍了深度森林算法的一大优势在于其无须大量设置超参数和调参。采用默认的超参数设置即可应对规模类型不尽相同的预测任务。因此,本文试验对深度森林算法采用默认的超参数设置。具体超参数设置见表1。
3.5 试验结果分析
利用训练样本集对深度森林预测模型进行训练,并对2015年1月10日当天96个时刻的负荷量进行了直接预测。不同分类算法利用前21天和前40天的历史数据的负荷预测的结果如图7、8所示。
从图7中可以看出深度森林算法的负荷预测曲线变化趋势与当天实际负荷量的变化相一致,并且能够有效地预测当天负荷峰谷值以及出现的时间,而其他分类算法均无法有效地预测负荷量的具体值以及负荷的变化趋势。同时,从图8可以看出,在增加训练样本的特征数量之后,虽然其他算法的预测准确度有所提高,但它们的预测精度依然低于深度森林算法。这进一步说明了采用默认的超参数设置的深度森林算法可处理不同规模的训练数据样本集。

表1 深度森林算法中超参数的设置Table 1 Hyper-parameter setting of deep forest

图7 利用前21天的数据负荷预测结果Fig.7 Results of load forecasting based on data of the previous 21 days
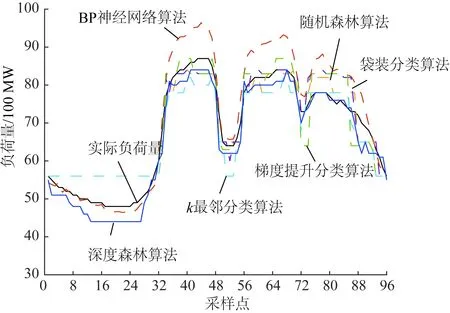
图8 利用前40天的数据负荷预测结果Fig.8 Results of load forecasting based on data of the previous 40 days
各个预测算法的负荷预测误差统计数据见表2。
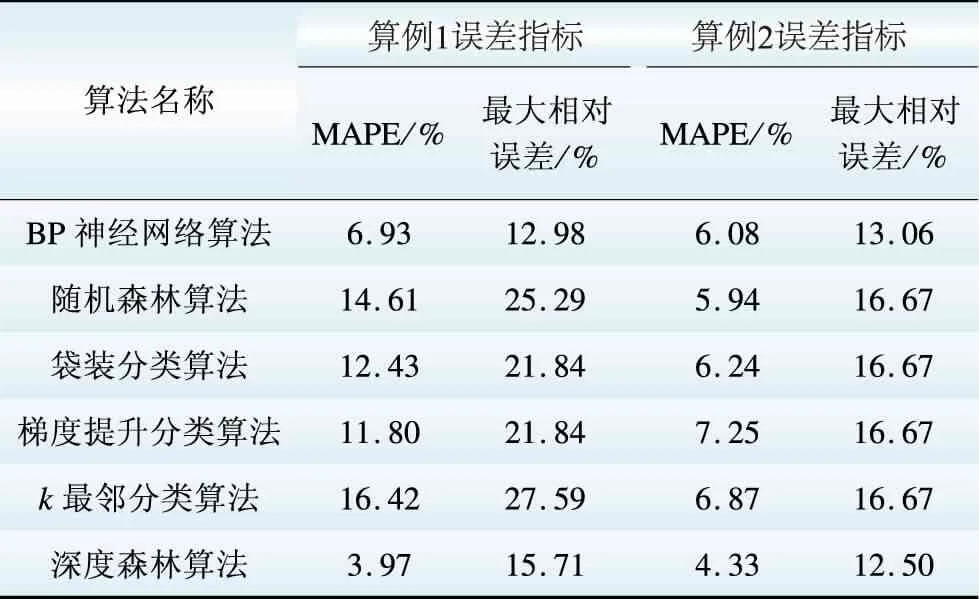
表2 各算法预测误差Table 2 Forecasting error of algorithms
从表2中可以看出,深度森林算法在所有试验算法之中,拥有最低的预测误差,展示了有效的电力系统短期负荷预测能力。
4 结 论
本文将深度森林算法引入电力系统短期负荷预测领域。选取了某地区的真实负荷数据、气象数据以及日期负荷数据,分别利用了前21天的数据和前40天的数据对深度森林模型进行训练,并运用深度森林算法进行电力系统短期负荷预测。试验中将深度森林算法与其他算法在短期负荷预测领域的性能进行了对比,验证了深度森林算法对电力系统短期负荷预测的有效性。该算法在文中的理论分析和试验分析中体现了以下特点和优势:
(1)深度森林算法受深度神经网络等深度学习理论的启发,设立多粒度扫描以及级联森林2个阶段。该算法具有处理表征关系的能力和逐层加强表征学习的能力。深度森林算法作为基于决策树的集成算法,不仅克服了深度神经网络超参数确定难度大的问题,而且在理论分析方面也比深度神经网络容易。
(2)采用了某地区的真实负荷值、天气数据以及日期负荷数据,检验了深度森林算法的短期负荷预测能力。作为分类算法,深度森林算法能够有效地预测负荷的具体值以及负荷的变化趋势,并在所有进行试验的算法之中,具有较低的预测误差。
(3)在深度森林算法保持超参数设置不变的情况下,试验验证了深度森林算法在不同的数据规模下均具有有效的短期负荷预测能力。同时,相较于其他分类算法,深度森林算法利用小规模预测样本即可达到较高的负荷预测精准度。因此,深度森林算法能够有效地处理规模不同的数据集,挖掘电力系统的各数据之间关系,提高短期负荷预测效果。

