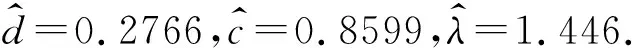累积损伤模型下Lomax分布产品循环序进应力加速寿命试验的可靠性统计分析
和 阳, 王蓉华*, 徐晓岭
(1.上海师范大学 数理学院,上海 200234; 2.上海对外经贸大学 统计与信息学院,上海 201600)
0 引 言
ABD ELLAH A H[1]将Lomax分布称为第二型的Pareto分布,该分布包含了单调递增和单调递减的失效率,在分析医学、生物科学和工程科学等方面的寿命试验数据处理中起着重要的作用.关于该分布的统计推断理论引起了很多统计学者的兴趣.XIAO和REN[2]研究了熵损失下两参数Lomax分布中尺度参数已知时形状参数的Bayes估计;ZHOU[3]研究了对数熵损失下两参数Lomax分布中形状参数的Bayes估计;WANG和REN[4]研究了Negative association(NA)样本下两参数Lomax分布中形状参数的经验Bayes检验;YAO和XIE[5]研究了在不同损失函数下两参数Lomax分布中尺度参数已知时形状参数的Bayes估计;YAO[6]得出了Linex损失函数下两参数Lomax分布中尺度参数已知时形状参数的Bayes估计及多层Bayes估计;YAO和WU[7]研究了在Linex损失函数下两参数Lomax分布中形状参数的E-Bayes估计,并运用Monte-Carlo随机模拟对各个估计值进行比较;LONG[8]研究了两参数Lomax分布次序统计量的性质和渐进分布,并在文献[9]中研究了两参数Lomax分布中参数的区间估计和假设检验;AMAL和AMANI[10]讨论了累积损伤(CE)模型下Lomax分布简单步进应力加速寿命试验的极大似然估计,以及参数的渐进方差-协方差矩阵,并给出了基于极大似然估计渐进正态性的区间估计,通过似然比的方法获得了参数的假设检验.本文作者讨论了累积损伤模型情况下,Lomax分布产品在循环序进应力加速寿命试验下的参数估计.
设某产品的寿命T服从Lomax分布,其分布函数与密度函数分别为:
(1)
(2)
其中,β为尺度参数,λ为形状参数.
1 逆幂律模型和Nelson假定
逆幂律模型是指在加速寿命试验过程中,电压作为加速应力,根据物理原理和实验经验,发现有些产品(如绝缘材料、电容器、微型电机和某些电子器件等)的尺度参数β(单位:h)和U电压(单位:V)之间有如下关系(称为逆幂律关系):
(3)
其中,d>0,c>0,且d,c都是常数.若产品是电子元器件时,物理实验表明c仅与元器件的类型有关,与其规格无关.
式(3)对两边同时取对数,则β满足对数线性关系:
lnβ=a+bφ(V),
(4)
其中,a=-lnd,b=-c,φ(V)=lnV.
步进应力或序进应力加速寿命试验的统计分析大多是建立在Nelson假定基础上的.
Nelson假定[11]:产品的残余寿命仅依赖于当时已积累失效的部分和当时的应力水平,与积累方式无关.
Nelson假定其实就是一种“时间折算”,即如果持续在一个恒定应力下,未失效产品会根据该应力下的分布函数来失效,但是要从以前累积失效的部分开始算起.
设在恒定应力Vi(i=1,2)下产品的寿命Ti服从Lomax分布,其分布函数为:
(5)
由Nelson假定知:
(6)
即
(7)
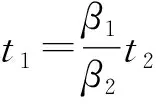
2 Lomax分布在循环序进应力V1=0加速寿命试验下的失效模式
循环序进应力V(t)是时间t的周期函数(周期为Z),且在一个周期内,V(t)是非负递增有界的连续函数.
设产品寿命为T,不妨假定t∈[0,MZ],将区间[0,MZ]分成M个周期区间[iZ,(i+1)Z],i=0,1,…,M-1.在每个区间内插入n-1个分割点,把区间分成了n个小区间,将M个周期区间的所有Mn个小区间的端点记为:
t0 其中,t0=0. 由循环序进应力函数V(t)的定义,一个循环的步进应力函数 (8) (9) 设产品在应力水平Vi下所经历的循环步加试验时间依次为ti-ti-1,i=1,2,…,Mn,其中t0=0.记τi-1为产品经历的各段试验时间折算到Vi应力下总的折算时间,根据Nelson假定,可得: (10) 定理产品在循环序进应力V(t)下寿命的分布函数为: (11) (12) 由Nelson假定可知: (13) 这相当于把[0,t]分割成i个小区间,当分割的细度λ→0时,由定积分的定义知: (14) 由此可得循环步进应力下的寿命分布函数为: (15) 考虑循环序进应力加速寿命试验,将n个产品随机分成p组,每组有ni个产品,分别在循环应力Vi(t)=Kit下独立地进行无替换的寿命试验,循环周期为Z,记下每个失效产品的试验循环次数,直到所有的产品失效试验停止.设第i类应力Vi(t)下ni产品的试验循环次数为yi1,yi2,…,yini,i=1,2,…,p. 设产品在任何循环序进应力下所承受的循环次数为X,某产品失效时,在循环应力下承受的循环次数为m,则概率为: (16) 关于αi和λi的似然函数为: (17) 对数似然函数为: (18) 求lnL(αi,λi)对αi和λi的偏导数,分别为: (19) 令 (20) (21) 即: lnαi=γ+clnKi, (22) (23) 由最小二乘法得到β的估计为: (24) 则参数γ的估计为: (25) 参数c的估计为: (26) (27) 取样本容量n=60,将样本分成4组,每组有15个数据,参数真值取为:k1=2.0,k2=3.0,k3=4.0,k4=5.0,c=1.0,d=1.0,λ=1.0,τ=0.4,通过Monte-Carlo模拟产生60个步进应力下的随机数. 第一组产品经历的循环次数为: 2,2,2,4,5,7,9,13,21,24,32,40,48,118,611; 第二组产品经历的循环次数为: 1,4,5,6,6,7,10,7,19,24,27,31,56,372,411; 第三组产品经历的循环次数为: 1,1,2,4,5,5,6,7,7,9,9,18,26,29,174; 第四组产品经历的循环次数为: 1,1,1,1,1,1,1,1,2,3,4,5,15,18,46.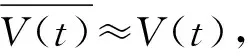
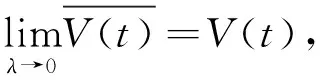
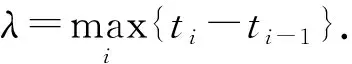
3 Lomax分布在循环序进应力(V1=0)加速寿命试验下的可靠性统计分析

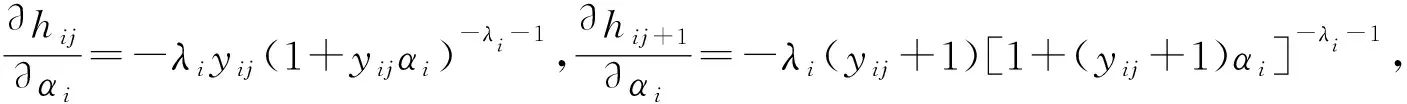
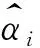
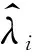
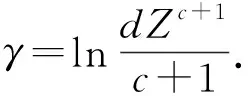
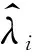
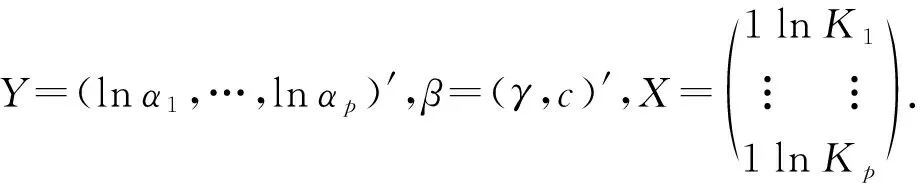

4 Monte-Carlo算例