垂直腔面发射激光器光功率-电流模型可靠性研究
陈虹豆, 李 莉, 罗汉文,2*
(1.上海师范大学 信息与机电工程学院,上海 200234; 2.上海交通大学 电子信息与电气工程学院,上海 200240)
垂直腔面发射激光器(VCSEL)自问世以来便被应用于光通讯、光互联、光交换、光存储以及光打印等诸多领域,并在其中发挥着重要的作用[1].由于VCSEL散热性较差,阻抗较大,器件的温度变化对其输出的光功率强度影响显著.随着偏置电流的增大,更多高阶模式满足阈值条件而激射,由此引起的载流子分布变化、空间烧孔现象以及热透镜现象,都将对VCSEL的横模特性产生影响[2].因此,建立一个考虑热效应的VCSEL模型就显得十分重要.
对于VCSEL,研究人员基于数值计算做了大量的研究,计算量非常巨大.文献[3]介绍了在电子设计自动化(ADS)软件上,如何用半分析法有效提取VCSEL小信号等效电路模型的参数,并对误差进行了分析,虽然减少了计算的工作量,但没有考虑温度升高对小信号模型特性的影响.
本文作者研究了基于测量数据的VCSEL的光功率-电流(L-I)模型,估计模型的有效参数,分析VCSEL正常工作的环境温度.
1 VCSEL的L-I模型
激光器是将电能转换成光能的半导体器件,在转换过程中,伴随着电子的运动,半导体器件会产生一定的热量.从能量守恒的角度看,转化为热能的能量越多,器件温度越高.
由于载流子扩散和空间烧孔对VCSEL性能的影响小于热效应,可以忽略上述空间效应.当考虑使VCSEL开始产生激光振荡的阈值电流对输出光功率的影响时,输出光功率和相应驱动电流、阈值电流应满足
P0=η(T)(I-Ith(N,T)),
(1)
其中:P0是VCSEL输出的光功率;I是注入到VCSEL的外部驱动电流,在直流情况下,等于外部加载的偏置电流;η(T)为VCSEL的能量转换效率,与VCSEL的温度T相关,温度T受外界环境温度T0和VCSEL自身的温度Ta影响,如公式(3);Ith(N,T)是阈值电流,VCSEL外部驱动电流超过该值,则VCSEL发光;N是载流子数.
假设η(T)受温度影响较小,η(T)近似于常数η,且
Ith(N,T)=Ith0+Ioff(T),
其中:Ith0是常温下的阈值电流,为常数;Ioff(T)是VCSEL内部的偏置电流,随VCSEL温度的变化而变化,一般称为经验热偏置电流,有别于外部人为加载的VCSEL偏置电流.
不失一般地,
(2)
其中,an为该多项式各阶次系数.温度T受外界环境温度T0和VCSEL自身的温度Ta影响,Ta与VCSEL产生的瞬时功率相关,即受VCSEL电压U、电流I特性影响.文献[4]中,
(3)
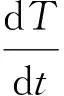
在直流条件下,综合考虑式(2)和(3),式(1)可变换为[5]:
(4)
式(4)即为垂直腔面发射VCSEL的L-I模型.
2 L-I模型参数的估计方法
根据20 ℃下实测的电压、电流数据,对VCSEL的输入特性进行建模.电压、电流特性曲线的斜率越小,VCSEL受到外部电流变化的影响越小,VCSEL的性能就越好[6].由于VCSEL的电压、电流特性通常是非线性的,故可对其进行多项式建模[7],
U=(b0+b1T+b2T2+…+bnTn)(c0+c1I+c2I2+…+cnIn),
(6)
其中,b0,b1,…,bn和c0,c1,…,cn是常数.在给定温度T条件下,第一个多项式近似为常数,式(6)可改写为
U=d0+d1I+d2I2+…+dnIn.
(7)
采用最小二乘法进行多项式拟合系数的估计,具体如下:
步骤一,根据20 ℃下VCSEL的实测数据{(Ui,Ii)|i=1,2,…,1402},计算各点到式(7)曲线距离的平方和
(8)
步骤二,为求得使M最小的d0,d1,…,dn值,对式(8)两边分别对dn求偏导数,
(9)
式(9)可化简为
(10)
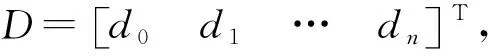
3 仿真实验
分别令n=2,3,…,6,得到不同次多项式,其拟合结果对比如表1所示.

表1 不同次多项式拟合结果对比
表1中,评价指标R2是度量拟合优度的一个统计量,其取值范围为[0,1],越接近1,表明模型对数据拟合的程度越好.
当最高次数达到5次后,评价指标R2逼近于1,且继续增大n后,评价因子变化很小,拟合程度较好.为在不增加计算量的同时减小误差,将n=5时得到的拟合系数d0,d1,…,d5代入式(7),可得到温度在20 ℃时,VCSEL 的电压、电流的特性模型
U=1.4+0.4424I-0.105I2+0.01425I3-0.000915I4+2.233×10-5I5,
(11)
如图1所示.

图1 20 ℃条件下,电压和电流实测及拟合数据的特性曲线
3.1 L-I模型的参数估计
将式(11)代入式(4),得到
(12)
式(12)反映了输出光功率随驱动电流的变化情况.
取n为4[8],结合各参数初始值和20 ℃下的实测数据,使用最小二乘法,估计的参数值分别为:η=0.288033947,Ith,0=0.277000898,Rth=4.35107303,a0=0.643568023,a1=-2.97473695×10-2,a2=3.14706509×10-4,a3=-2.48571163×10-7,a4=7.98200038×10-10.
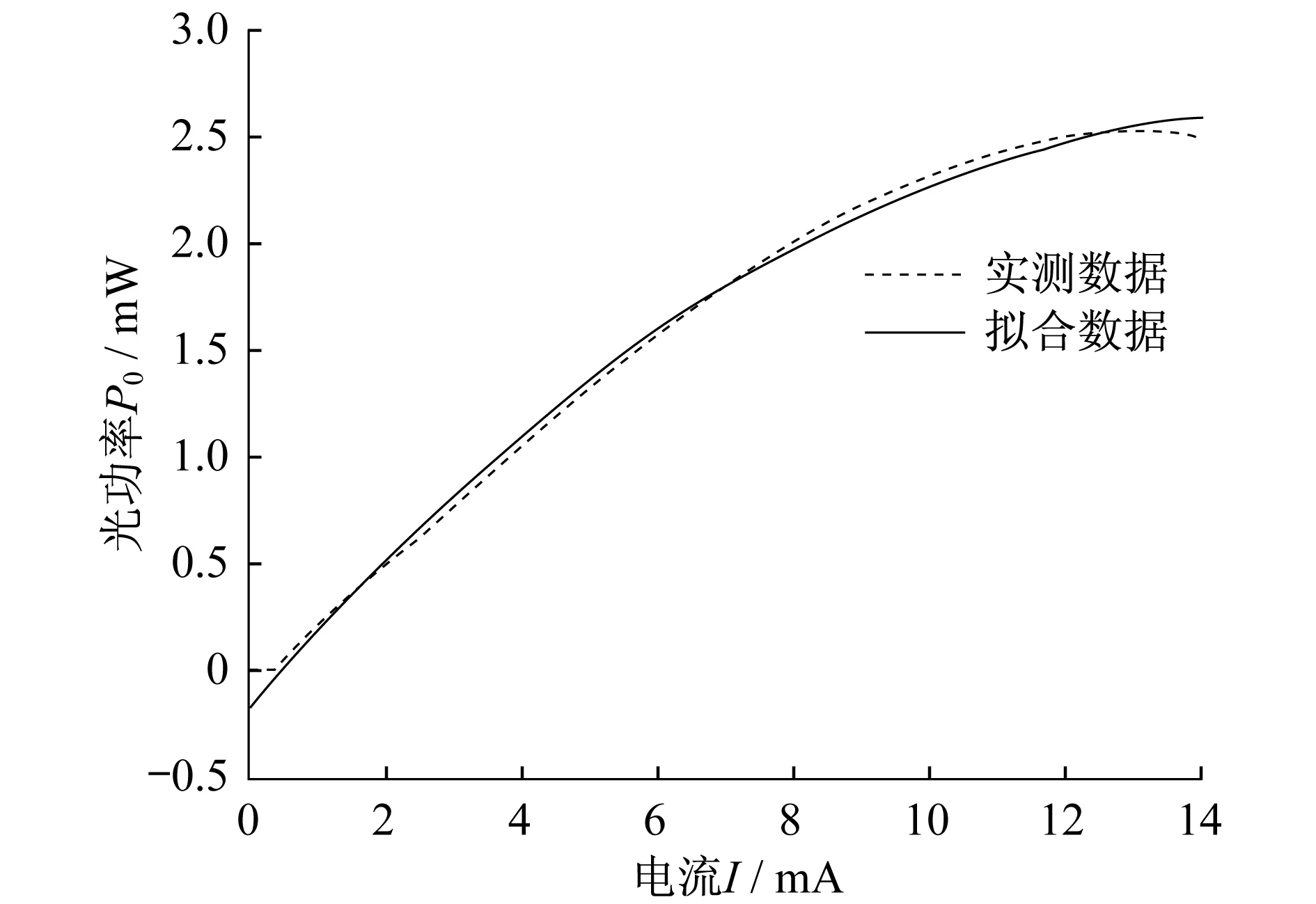
图2 20 ℃条件下,L-I实测及拟合数据的特性曲线
在20 ℃条件下,将求得的参数代入式(12)中,由于驱动电流已知,得到拟合的P0.将与实测驱动电流{Ii,i=1,2,…,1402}一一对应的P0拟合值,与20 ℃时的实测数据进行对比,检测得出的参数值是否准确,结果如图2所示.
由图2可知,在20 ℃时,仿真模拟的光功率、电流曲线与实测曲线基本吻合,整体误差较小,由此可得所求估计的参数较准确.
3.2 L-I模型的VCSEL温度特性分析
假设VCSEL在不同温度下电压与电流关系保持不变,仿真模拟出T0分别为10,20,30,40,46,50,60,70,80,90 ℃时的L-I曲线,如图3所示.

图3 不同温度T0下L-I曲线
当VCSEL在直流输入情况下,P0低于2 mW时,用户的光调制解调器无法检测到信号.由图3可以看出:当T0<46 ℃时,光功率P0均可高于2 mW,用户的光调制解调器均可检测到信号以保证网络的正常使用.要保证用户可以正常使用网络,T0为10 ℃时,I应大于7.90 mA;T0为20 ℃时,I应大于8.00 mA;T0为30 ℃时,I应大于8.45 mA;T0为40 ℃时,I应大于9.45 mA且小于13.80 mA.
另外,P0随着I的增大,最终都呈现出下降趋势,设想当I足够大时,P0下降为零,即VCSEL被击穿,其仿真模拟结果如图4所示.

图4 VCSEL被击穿时L-I模拟曲线
从图4中可以看出,VCSEL在T0为90 ℃被击穿时的I为14 mA;T0低于90 ℃时,击穿电流I约为24.00 mA,但在此之前,VCSEL已无法正常工作.
4 结 论
本文作者建立了一个比较接近实际的VCSEL L-I模型,仿真结果与实测数据吻合得较好,精确度较高,比较真实地反映了VCSEL的特性,证明了该模型的有效性,并全面地分析VCSEL在不同温度条件下的工作状态,避免由于温度过高而造成不必要的损失.然而,在估计模型参数时,对误差范围做了一些近似处理,并没有考虑到VCSEL材质对散热的影响,这将是下一步的研究内容.

