基于超椭球模型的T-S模糊因果图的故障分析*

吴成姚，王洪春

(重庆师范大学 数学科学学院，重庆 401331)

目前，复杂系统的故障诊断是人工智能的核心问题之一，它的方式也是多样的，比如贝叶斯网络[1-2]、故障树[3-4]、有向图、认知图、因果图[5-7]等。而由张勤教授提出的因果图推理方法更加扩大了复杂系统故障诊断的应用。樊兴华[7]提出了多值因果图的推理算法研究；王洪春[8]提出了因果图不确定性推理及其结构的学习；沈文武等[9]提出了因果图迭代推理算法以及专家系统的应用研究。然而在一些复杂多样的故障机理、数据缺乏等问题上还无法有效获得概率值，于是利用超椭球模型来对因果图基本事件的区间概率加以约束，以及用T-S模糊门来描述事件间的联系，使其因果图对故障数据的缺乏和故障机理不再进行深入研究，解决了事件间的不确定性问题。

1 因果图

因果图是由张勤教授[7]提出来的，用图形化的方式使因果知识表达直观，更加容易分析处理。图1就是典型的因果图，它可以表示系统中因果关系，处理或推断系统中的不确定性问题，还可以进行由因到果的正向推理和由果到因的反向推理以及正反向混合推理。在因果图中，用圆圈表中间事件，可将它视为现象，方框表基本事件，可将它视为故障，中间事件和基本事件统称为节点事件；门节点通常表示“与”门、“或”门等，有向边表示“连接事件”、“可以事件”之间的关系，使其在不确定性的因果间知识表达更加清楚明了，更有意义。

图1 因果图Fig.1 Causality diagram

梁新元等[5]在因果图向故障树的转换应用中，使因果图模型更好地扩大了应用范围，便于故障树建模；在故障树向因果图的转换[6]应用中，也能够更好地运用到复杂系统中。于是在采用故障树分析方法(FTA)与因果图法的相互转换中，因果图模型能够发挥更大的作用。

2 D-S理论的T-S模糊因果图

2.1 T-S模糊因果图描述

在因果图中描述事件间的联系往往具有不确定性，大多情况下系统的故障机理也不清楚，因此本文将因果图中节点事件作为树根得到微因果树，将其过程转化为T-S模糊因果树(图2)，用T-S模糊门代替因果图中的“与”门、“或”门[10]，处理不确定性的问题。T-S模糊因果树如图3所示。

2.2 D-S理论描述

因果图的故障诊断在一些复杂多样的故障机理、数据缺乏等问题上还无法有效获得概率值，因此本文用区间数来描述事件发生概率。

用Dempster[12]，G.Shafer[13]提出的D-S证据理论来处理不精确推理问题。在D-S理论中，一个推测空间描述为一个“辨识框架”，用符号Ω表示，它由一些完备的互不相容的元素组成。D-S证据理论的基本概率分配函数(m函数)，满足条件：

0≤m(A)≤1

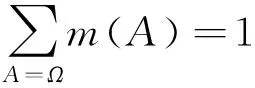
m(∅)=0

其中，∀A⊆Ω，∅为空集，m(A)表示A的Mass函数或基本概率函数。

A的信任函数Bel：2Ω→[0，1]表示为

其中，Bel(A)是总的信任，表示所有A的子集的精确信任程度的和。

A的似然函数Pl：2Ω→[0，1]表示为

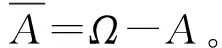
于是，用D-S理论确定了因果树基本事件故障概率区间[Bel(A)，Pl(A)],然后由D-S理论的合成公式得：

图2 因果图1对应的因果树Fig.2 Causality tree

图3T-S模糊因果树

Fig.3T-Sfuzzycausalitytree

其中,m1(A)表示根据证据A的Mass函数；m2(B)表示根据证据B的Mass函数；m(C)表示总的Mass函数。

2.3 结合D-S理论的T-S模糊门算法

1985年，Takagi和Sugeno两位学者提出T-S(Takagi Sugeno)模糊模型，它是一种万能逼近器，由一系列IF-THEN模糊规则组成，可用来表示事件间的联系，从而构成T-S模糊门。

设基本事件B1，B2，…，Bn的上级事件为Y，则它们之间的联系可由图4所示。

图4 T-S门Fig.4 T-S fuzzy gate

若有Bi(i=1，2，…，n)个基本事件，则B1，B2，…，Bn发生的概率区间表示为[Bel(xi)，Pl(xi)]。

如果各基本事件发生故障概率为

因此上级事件Y的模糊可能性为

图5 二维区间模型Fig.5 Two dimensional interval model

于是利用区间数的运算规则：

(5)

由图5和式(5)可看出，基本事件的发生区间概率必须同时取边界值时，才能得到上级事件发生概率区间的边界值。而在实际工程中，基本事件发生的区间概率同时取边界值的极端情况的概率比较小，因此，用区间数的T-S模糊因果图的方法来计算，结果偏于实际。

2.4 结合超椭球模型的T-S模糊因果图

由于区间模型在实际工程中，基本事件发生故障概率的区间同时取边界值的极端情况比较少，采用超椭球模型对区间加以约束[14-15]，如图6所示，超椭球模型更合实际。

图6 二维区间模型与二维超椭球模型Fig.6 Two dimensional interval model and two dimensional super ellipsoid model

于是由D-S理论可以表示基本事件发生的区间概率:

用超椭球模型可描述为

(6)

各基本事件的发生概率区间要满足式(6)的超椭球区域内部，为此引入矢量y=DP，其中，

y=(y1，y2，…，yn)T

将原超椭球模型转成单位超椭球模型

(y-y0)Τ(y-y0)≤1

令Δy=y-y0，由式(7)知，在超椭球内产生均匀分布的随机数，相当在Δy空间单位超椭球体内进行均匀采样。

设单位超椭球体[14-15]的坐标为(r，θ1，θ2，…，θn-1)，r∈[0，1]，θi∈[0，2π]，i=1，2，…，n-1，则它们之间关系转化为

(8)

于是由式(8)得出基本事件的发生区间概率为

则T-S规则l执行的可能性区间概率为

因此上级事件Y的模糊可能性的概率为

3 实 例

在复杂系统中，由于数据的缺乏以及一些多样的故障机理，很难获取精确值和事件之间联系的不确定性，都会增加因果图的不确定性，因此采用区间分析、T-S模糊门进行分析。以图7故障系统为例，根据专家经验与历史数据构造T-S门规则表，如表1、表2，用D-S理论确定出其区间概率[15]。假设基本事件B1，B2，B3发生故障程度为1的区间概率分别为[9.7×10-6，1.02×10-5][1.7×10-6，2.2×10-6]，[4.5×10-6，5.0×10-6]，在故障程度为0.5的区间概率相同，结合公式(3)(4)(6)，求得概率区间。图7中B1，B2，B3，y1，y2分别为控制系统、电动执行器、球阀、电动阀门控制器和电动球阀的故障程度。

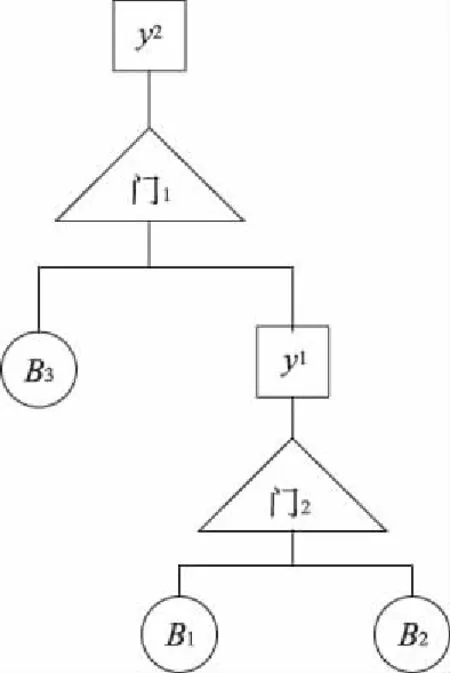
图7 电动球阀故障系统Fig.7 Fault system of electric bally

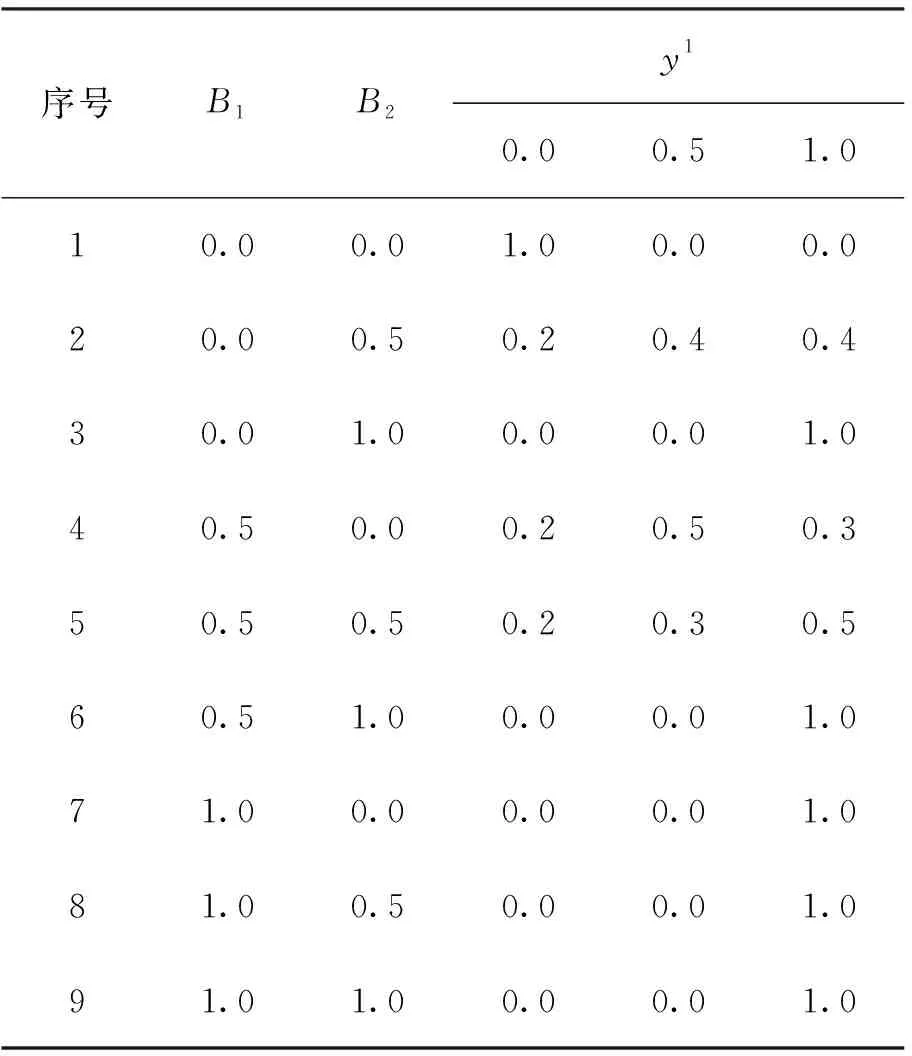
序号B1B2y10.00.51.010.00.01.00.00.020.00.50.20.40.430.01.00.00.01.040.50.00.20.50.350.50.50.20.30.560.51.00.00.01.071.00.00.00.01.081.00.50.00.01.091.01.00.00.01.0

表2 T-S模糊门2Table.2 T-S fuzzy gate 2

表1、表2中的每一行为一条模糊规则，如表1第5行代表的规则：若B1为0.5，B2为0.5，则y1为0的概率为0.2，为0.5的概率为0.3，为1 的概率为0.5。

[1.862 5×10-5，2.128×10-5]

[1.6776 5×10-4，1.948 4×10-4]

[2.37×10-5，2.916 4×10-5]

[1.692 6×10-3，2.177 1×10-3]

而利用超椭球T-S模糊因果图方法得出的区间概率为

[1.892 5×10-5，2.087 5×10-5]

[1.688 7×10-5，1.807 7×10-5]

[2.416 4×10-5，2.863 5×10-5]

[1.702 1×10-3，1.987 8×10-3]

可见，超椭球T-S模糊因果图与区间T-S模糊因果图得到的区间概率宽度较小，避免了基本事件发生的区间概率同时取边界值这一极端情况的发生，结果更为合理，能够更好地分析系统的实质。

4 结 论

在实际系统中，基于因果图很难获取精确值与不确定性事件之间的联系的情况下，提出了基于超椭球模型下的因果图分析方法，避免了因果图难以获取精确数据的问题；并采用T-S模糊因果图，解决了零部件故障概率与系统故障机理不确定性的问题，同时不用精确挖掘基本事件发生的概率，使因果图模型更加具有实际意义。