基于深度神经网络的中期电力负荷预测*

王 军

(安徽工程大学 电气工程学院，安徽 芜湖 241000)

0 引 言

电力负荷预测在电力系统调度、维护和容量规划等方面起着至关重要的作用。实际的电力负荷预测分为短期、中期和长期预测。短期负荷预测(Short Term load Forecasting，STLF)与未来几小时到几天的负荷预测相关，中期负荷预测(Medium Term load Forcasting，MTLF)则处理以几周到几个月为目标的预测，长期负荷预测(Long Term load Forecasting，LTLF)则是处理一年到几年的负荷预测。LTLF可以协助规划新的电力系统；MTLF有助于系统维护、购买能源和定价计划；而STLF在配电和负荷调度中起着关键作用[1]。STLF是一项及具有挑战性的任务，因为它需要在较短的时间内完成及时和准确的决策。

目前，已经有许多科研工作者研究了不同的方法来准确预测近年来的用电负荷。传统的统计负荷预测方法不足以充分模拟电力需求的复杂性，往往导致精度较低[2]。随着人工智能(AI)技术的发展，由于它们能够解决独立变量和独立变量之间的非线性关系，因此被广泛应用于电力负荷预测中。模糊逻辑[3]、人工神经网络[4]、支持向量机[5]和小波神经网络[6]等流行的AI技术已被用于MTLF。目前，深度神经网络方法在图像处理方面已经取得了最先进的成果，因此也可以将它们用于一般的时间序列建模任务，例如用于负荷预测的任务。Busseti等[7]通过深度神经网络和递归神经网络进行了电力负荷预测，但仅利用了时间和温度数据来预测负荷需求；Khan等[8]提出了一个递归神经网络模型可实现提前半小时的负荷预测；郭欣欣等[6]开发了ANN模型用于1 h前的电价预测。

本文提出将FF-DNN和R-DNN模型用于中期电力负荷预测。为了在预测中获得更高的准确度，提出一种新的时域-频域特征提取方法。首先，独立地分析时域和频域上的数据，随后将频域分量转换回时域数据，由此产生的时频特征可以有效地捕捉到影响负荷的主要因素即天气、工作时间和非工作日、滞后负荷和数据分布效应；然后，进行基于FF-DNN和R-DNN模型的中期电力负荷预测，并在MAPE误差测量的基础上比较深度神经网络的预测性能。

1 基于时域-频域分析法的数据预处理

由于电力负荷原始数据集中包含着大量非线性信息，且各种因素对用户情况的影响非常复杂,因此需要观察不同的时间段内，天气、时间、假日和负荷分布等因素对日耗电量的影响。该部分研究工作将分别从时域和频域的角度提取特征，然后进行时域和频域的数据转换，并用于深度神经网络模型预测电力负荷。

1.1 时域特征提取

对原始数据集进行时域分析，以捕捉耗电模式随时间变化的规律，效果如图1所示。通过分析可见每个月内的负荷数据按每周呈现出周期性规律且具有以下4点特征：

(1) 温度影响。一周内每天的用电量受温度影响较大，需要根据环境变化使用不同的电力来保持温度适宜,同时为了在夏季和冬季保持湿度，也需要消耗不同的电量。已选择干球和露点功能来表示温度对用电量的影响。

(2) 工作日和非工作日影响。周一至周五，耗电量高，周六和周日耗电量低，基于此观察，选择“工作日特征”来表达这种影响。

(3) 时间影响。图1还表明，电力消耗在很大程度上取决于时间，电力消耗值分别在中午前上升，中午后下降。

(4) 数据分布影响。将使用偏度、峰度、方差和周期性等指标来挖掘过去24 h内的负荷数据特征。通过这些功能可以高效地发现数据集中的隐藏模式，并帮助神经网络提供最高的负荷预测准确度。

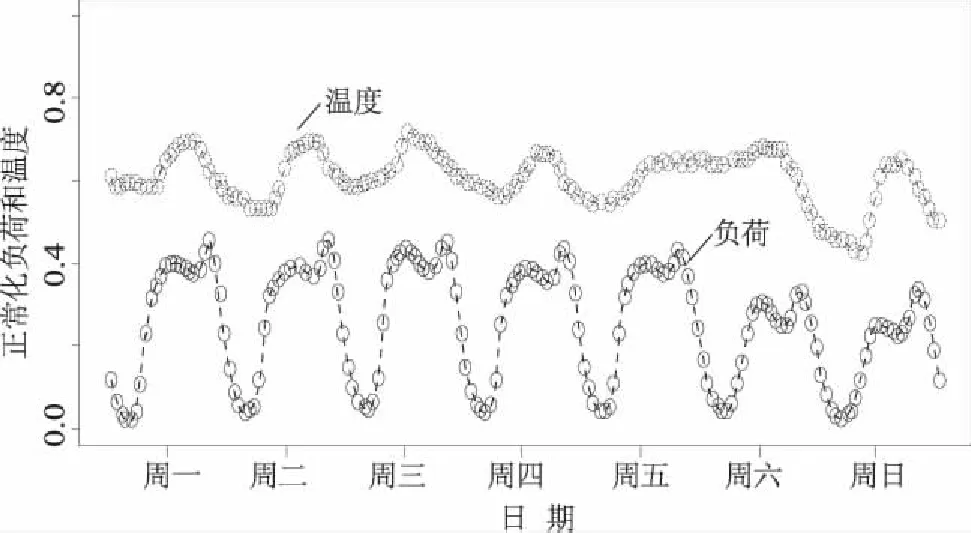
图1 一周内温度和负荷关系曲线

1.2 频域特征提取

时域数据分析可以提供用电量变化行为的潜在特征，然而由于缺乏表达隐藏在数据集中的复杂性功能，时域分析获得的特征没能提供更高的准确性，因此需要进一步进行频域数据分析以揭示这些隐藏模式。频域分析是将时域信号分解成各种频率的多个正弦波，并且将这些时域随机信号转换成稳定且易于预测的不同频率信号，从而大大提高准确性。对电力负荷数据值执行快速傅里叶分析以确定主要频率。式(1)可将负荷值转换为非标准化单变量离散傅里叶变换序列：

(1)

其中，x(n)代表时域信号；y(k)表示变换过后的频域信号；N是输入信号的长度。

2 深度神经网络模型

人工神经网络通过模拟人类大脑的工作机理，学习数据中隐藏的非线性和复杂结构，从而达到模拟人脑的认知和学习能力。2006年,Hinton等[10]学者提出了深度置信网络(Deep Belief Networks，DBN)，该网络是一种无监督的概率生产模型。深度神经网络(Deep Neural Networks，DNN)是由训练好的DBN和一个与目标相关的输出层构成。由于DNN训练优化更容易，因此在机器学习的领域掀起了热潮。在本文工作中，提出将FF-DNN和R-DNN模型用于未来一天和一周的短期负荷预测。

2.1 前馈深度神经网络(FF-DNN)

神经元是FF-DNN模型的基本单元，结构上受人类神经元的启发。FF-DNN本质上是一个包含多个隐层的多层感知机，由输入层、隐层和输出层构成。设在FF-DNN模型中，包含L个隐层，输入为h0=X，则隐层的激活值与第t层神经元的权重wt和偏差向量bt之间满足以下等式：

其中，f(.)表示隐层节点的非线性激活函数。FF-DNN的基础目标是得到近似函f(.)，使用最多的传统激活函数是sigmoid激活函数，其表达式为

整流线性单元(Rectified Linear Unit，ReLU)激活函数是目前主导使用的非线性激活函数。

FF-DNN的输出层通常采用softmax函数进行建模，如式(2)：

(2)

其中ys表示输出向量中的第s个元素。

多层前馈神经网络的每一层都由许多个这样的神经元连接而成，模型的输出由权重和偏差决定。网络的学习过程就是在大量训练样本数据中通过调整权重使损失函数最小。损失函数定义为

Loss(q|W，B)

其中q是训练样本中的每一个数据；W是权矩阵；B是样本集。

2.2 递归深度神经网络(R-DNN)

多层感知是R-DNN中最简单的形式，一个隐含层的输出作为反馈层的输入。通过下列非线性等式来划定R-DNN的功能：

Q(t)=f1(X(t)*Wi+Q(t-1)*Wtd)
Y(t)=f2(Q(t)*Wi)

其中,X(t)是t时刻的输入；Q(t)是输出；Q(t-1)是t时刻的输入；Wi是输入层权重；Wtd是时滞输入的权重；Wo是输出层权重；f1和f2分别是隐含层和输出层传递函数。时滞单元通过输出和反馈的下一个时刻获得。R-DNN的结构图如2所示。

图2 R-DNN 结构图

基本结构是一个前馈DNN，但某些隐层具有与其自身完全连接的特定隐层，与前馈隐层处的那些神经元相对应的值可以表示为

其中n是前馈隐层数；sigmoid和softmax函数均是基本元素操作；X0是输入特征向量；Xi是非线性激活函数；yi是第i隐层的神经元向量。

(3)

其中Wii和bii是递归权矩阵和偏差向量。

3 中期电力负荷预测方案设计

该研究方案中，第一步是从原始数据中挖掘影响用电量的重要因素。为了实现这个目标，分别从时域和频域分析数据集，温度、时间、假期、负荷滞后和数据分布被认为是影响负荷量的主要因素。

第二步是选择优化模型参数。首先选择FF-DNN模型的参数，文中神经网络激活函数选用RELU激活函数，定义为

RELU激活函数的优点：由于适用于未标准化的数据，因此RELU激活函数处理时间短；不存在梯度消失问题。

第三步是利用预处理过的数据集进行神经网络的训练及预测。

整体研究方案设计流程如图3所示。

图3 负荷预测可视化流程图

4 实例分析

为了验证本文提出的FF-DNN和R-DNN算法在中期电力负荷预测中的优越性能，该部分仿真实验数据采用某市2007—2011年的负荷数据作为训练样本集，对2012年不同季节的负荷进行预测。训练样本集包括43 824组数据，测试数据集预测1周168 h和1月720 h的预测点。为了衡量该方法的有效性，将2012年的预测数据按照不同季节计算出MAPE预测误差。

首先，仅采用时域数据特征，利用FF-DNN和R-DNN进行周和月的电力负荷预测。由于不同季节的温度变化不同，用电量变化较大，因此该研究分别对冬季、春季、夏季和秋季分开进行负荷预测。利用FF-DNN和R-DNN进行时域负荷预测的MAPE误差如表1和图4所示。由图4可见夏季预测误差最大，这是由于夏季存在高温和社会事件使得用电量不可预估。

其次，利用时域和频域分析的复合特征数据进行基于FF-DNN和R-DNN模型的周和月的电力负荷预测。MAPE预测误差在表1和图5所示。由图5可见，采用该方法得到的预测误差比图4中的误差低很多。

表1 时域-频域FF-DNN和R-DNN误差

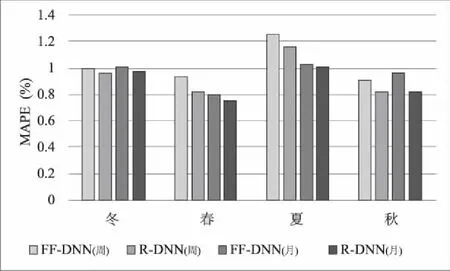
图4 时域MAPE误差对比

图5 时域-频域MAPE误差对比

5 结 论

开展了FF-DNN和R-DNN算法在中期电力负荷预测中的应用研究，提出了一种新的数据挖掘时域-频域分析方法，该方法能够从原始电力负荷数据中获取影响电能使用的最主要因素。通过实验仿真结果可见，天气、时间、假期、滞后负荷及其数据分布是影响用电量周期的主要因素。同时，通过计算MAPE预测误差来比较时域特征和时域-频域特征，展示了时域-频域法的优越性。