多基地声呐融合探测关键技术研究

张浩宇, 韩一娜, 赵伟康, 杨益新, 刘清宇



多基地声呐融合探测关键技术研究

张浩宇1, 韩一娜1, 赵伟康1, 杨益新1, 刘清宇2

(1. 西北工业大学 航海学院, 陕西 西安, 710072; 2. 海军研究院, 北京, 100073)

为了解决多基地声呐中的融合探测问题, 文中分别探讨了多基地声呐融合探测中的测量模型、数据关联和跟踪器性能模型3个关键技术。测量模型包括时间、方位、位置和声速的误差分布和目标的定位表达式, 给出了各个误差因素的表达式和定位误差的表达式。数据关联用来解决得到的测量与已知目标之间的分配问题, 重点介绍了最近邻数据关联和多假设数据关联方法, 这2种方法使用相同的数据模型、测量模型和运动模型, 通过对最近邻数据关联和多假设数据关联进行仿真, 发现均能对目标实现良好的跟踪。跟踪器性能模型用来评估跟踪器输出质量, 分别从跟踪检测概率、跟踪碎片和错误跟踪率3个性能指标评估输出质量, 通过仿真得到的性能指标可知, 多假设数据关联跟踪器的输出质量明显优于最近邻数据关联跟踪器的输出质量。

多基地声呐; 测量模型; 数据关联; 跟踪器性能模型

0 引言

由于浅水环境的复杂性以及潜艇的安静特性, 使得传统收发合置型主动声呐以及纯被动型声呐在反潜方面越来越难。主动声呐在发射信号时可能会暴露声呐的位置, 很容易被打击。纯被动声呐的探测能力十分有限, 高虚警率会进一步削弱其探测能力。多基地相对于收发合置声呐和纯被动型声呐有以下优势: 隐蔽性好; 抗干扰性强; 探测范围广; 定位精度高; 配置方式灵活; 设计易于优化等[1], 所以, 基于多基地声呐网络探测技术越来越受到重视。文献[2]中包括了数据关联技术, 但是没有多假设数据关联。基于此, 文中增加了多假设数据关联并进行仿真, 由跟踪检测概率、跟踪碎片和错误跟踪率3个性能指标建立的跟踪器性能模型是文章的创新点之一。

文中探讨的多基地声呐融合探测中的关键技术包括如下几个方面:

1) 针对目标测量数据开发统计学一致的测量模型, 以解决各种系统和测量误差[3];

2) 利用最近邻、多假设数据关联, 开发具有复杂性和性能增加的多基地能力[4];

3) 建立跟踪器性能模型, 评估跟踪器的输出质量[5]。

1 多基地测量模型

多基地声呐网络是由分布在监视区域内的多个声呐发射源和接收器组成。1个发射源与1个异地的接收器组成的网络称为双基地网络(见图1)。双基地网络是多基地网络的基本组成单元, 因此以双基地为例说明多基地情况。所谓测量模型就是对定位有影响的误差函数。定位误差来源包括发射源和接收器位置的误差、声速误差、时间误差以及目标方位误差函数。建立测量模型的目的是综合各种误差对定位带来的影响, 误差越小, 算法就能更好地进行数据关联。

图1展示了1对发射源—接收器的双基地发射源—目标—接收器几何形状, 发射源和接收器不在同一地点。假设忽略发射源、目标及接收器深度的影响, 研究对象在2D平面, 忽略多路径到达(在远距离情况下, 假设信号处理器成功地将单路径和多路径到达组合成单个目标接触点)。这些假设在许多低频主动声呐的监视应用中是合理的。而对于非常接近发射源和接收器的目标, 此假设无法使用。

1) 发射源—目标—接收器的时间

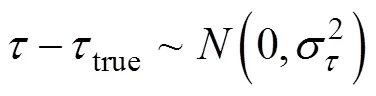
2) 目标相对于接受的方位角

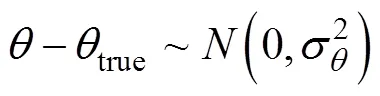
3) 接收器位置

4) 发射源位置

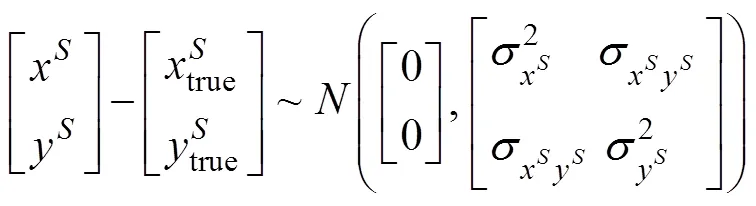
假设测量误差是不相关的(注意这仅是简化, 因为在波束形成过程中, 方位估计依赖于声速)。目标定位误差方差

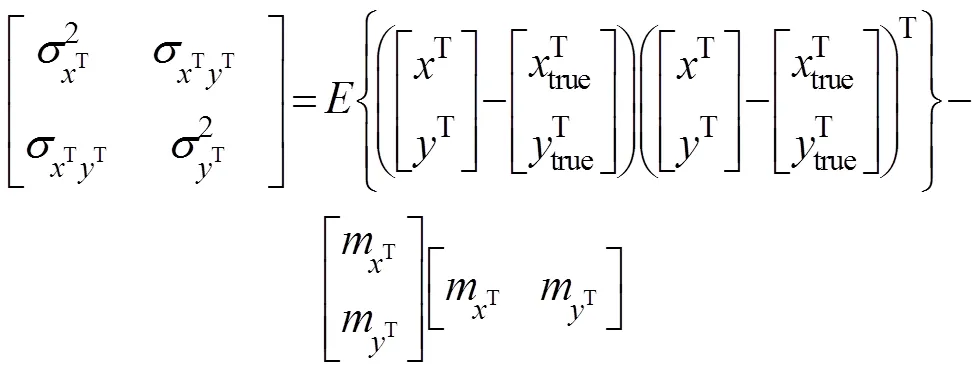
其中

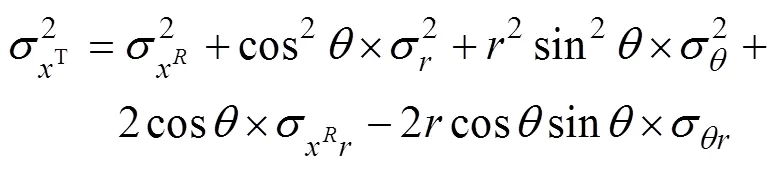
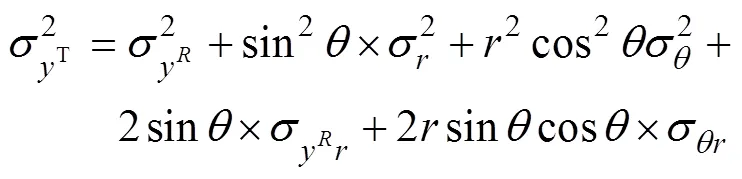
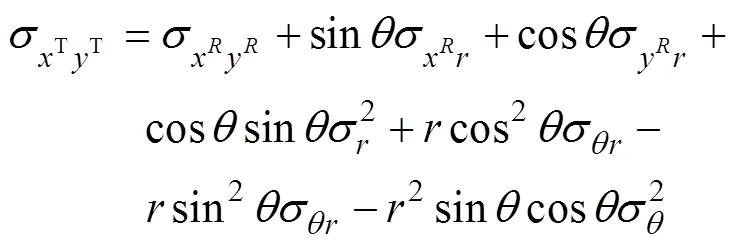
2 数据关联

通过上述测量模型可得到定位误差表达式。定位误差对数据关联有很大的影响: 误差越大, 关联的精度越低。可以把测量模型看作数据关联的前提条件。

数据关联就是把得到的测量与已存在的目标轨迹进行关联。常用的数据关联方法有最近邻数据关联、全局最近邻数据关联、概率数据关联以及多假设数据关联等。

1971年, Signer等[6]提出最近邻数据关联方法, 用于对目标状态进行预测。落入关联门内且和预测位置最近的一个点被称为关联点。“最近”并不是真实距离最小, 而是统计意义上的距离最小。最近邻数据关联则是将每个观测点迹与最近邻的航迹进行关联, 其优点是计算量小、便于实现, 适用于目标密度小、信噪比高的情况。缺点是最近邻关联是局部最优, 所以离中心最近的测量并不一定是正确的目标测量, 且抗干扰能力差, 多目标情况下容易产生错误的跟踪。

全局最近邻数据关联方法是在最近邻数据关联的基础上提出的。与最近邻数据关联不同的是, 全局最近邻数据关联会在最终给出一个唯一的观测点迹和航迹对。全局最近邻数据关联是求航迹与点迹之间的距离和最小, 用它来表明二者的靠近程度[7]。

1972年, Bar-Shalom和Jaffer[8]提出概率数据关联方法。一般情况下, 落在关联门的测量不止一个。按照最近邻数据关联的思想, 距离预测位置最近的测量来自真实目标, 但是事实可能并非如此, 而使用概率数据关联就能很好地解决此类问题。概率数据关联认为所有关联门内的测量都有可能来自真实目标, 只是概率不同。

多假设数据关联方法最早由Reid[9]提出。在每次扫描的测量可能来自杂波、新目标或已存在的目标的基础上, 多假设构造面向测量的关联假设树, 对每个测量列出可能的假设, 当数据关联发生冲突时, 形成多种假设延迟逻辑判断的决策。该方法的优点是, 延迟判决减少关联错误的概率, 跟踪精度高, 不易出现误跟踪或者丢失跟踪: 缺点是过于依赖目标或杂波的先验知识, 且计算量很大, 实现起来较为复杂。

该节主要介绍最近邻数据关联和多假设数据关联2种方法, 这2种方法的测量模型、运动模型和数据模型均相同。测量模型上节已经介绍, 现在介绍数据模型和运动模型。

2.1 数据模型

2.2 运动模型

文中使用近匀速运动(near constant velocity, NCV)模型[10]

连续时间动力学方程离散化模型为

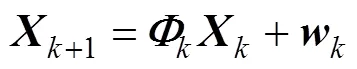
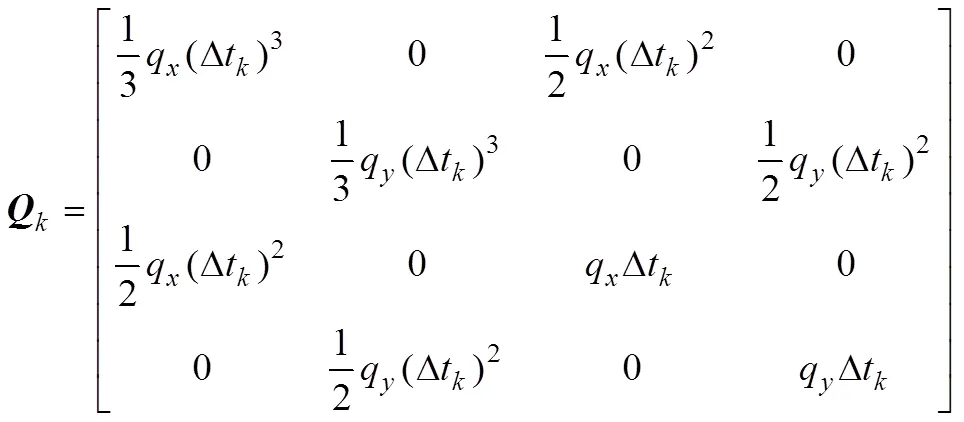
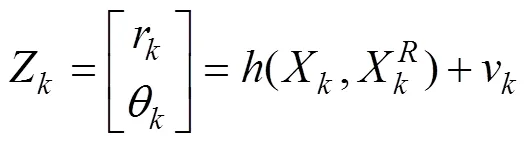
2.3 最近邻数据关联

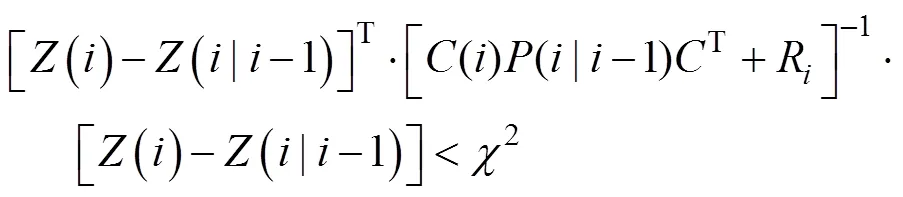
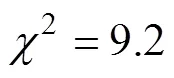
当次扫描内关联个接触时, 该航迹被确认: 若不然则此次跟踪依旧被放弃。如果已确认的航迹在连续次扫描中没有扫描到, 则终止此次跟踪。

2.4 多假设数据关联

多假设数据关联主要内容包括数据聚簇、假设生成、假设概率和假设支剪。

2.4.1 数据聚簇

聚簇指跟踪门的集合, 表示目标与测量存在一定的关系。在整个监测区域内, 可以把目标和测量分割为多个独立的簇, 这样就可以用若干个小的跟踪问题代替一个大的跟踪问题, 降低计算量和算法复杂度, 节省计算时间。程序初始化阶段分别为每个确认航迹创建独立的簇, 落入目标航迹跟踪门的测量都可以关联到簇内。下一次扫描收到的测量与以前的簇(假设)进行互联, 形成新的簇。若上一周期处理中2个或更多独立的簇与同一个量测相关, 则这几个簇形成1个新的超簇; 不与任何旧簇相关的测量形成新簇。

2.4.2 假设生成

假设就是关联, 是对簇内的测量进行分配, 测量可能来自先前存在的目标、新目标或杂波。1个簇内可以有多个假设, 每个假设可以包含若干个相容的航迹。对簇内的目标和测量进行关联生成假设的同时, 需要修改簇中每个假设的概率和目标的状态。

2.4.3 假设概率

上式等号右边第1项是给定分配假设条件下测量的似然值

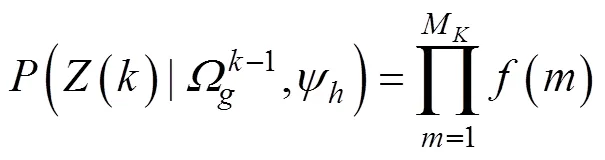
上式等号右边第2项

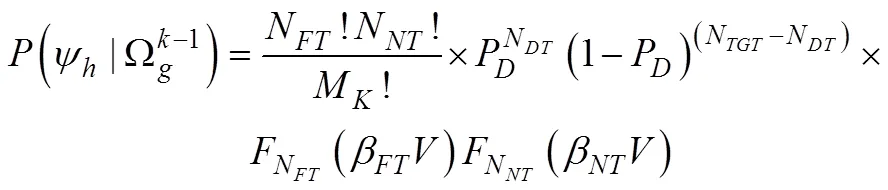
将式(9)和(10)代入递归公式并简化, 得到假设概率

2.4.4 假设支剪

通过删除低概率假设达到假设支剪的目的, 从而减少计算量。一般使用-Scan支剪法。

3 跟踪器性能模型

3.1 传感器模型

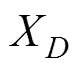
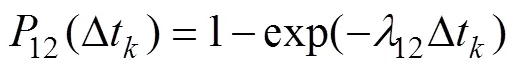
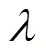
3.2 性能建模

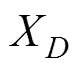
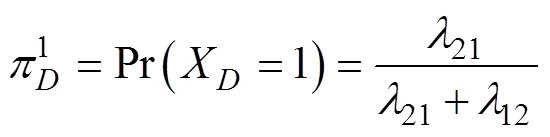
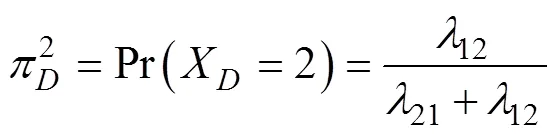
可得

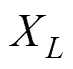
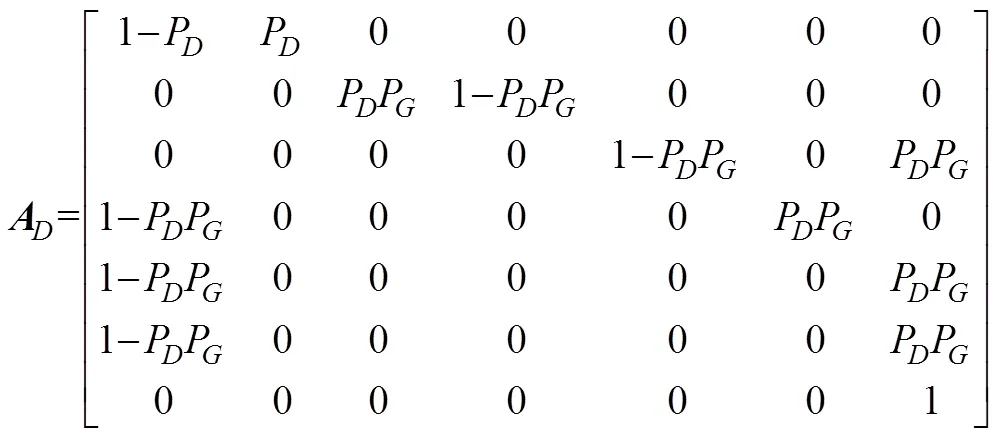
(18)

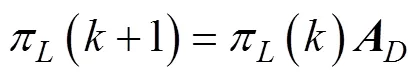
平均跟踪确认时间

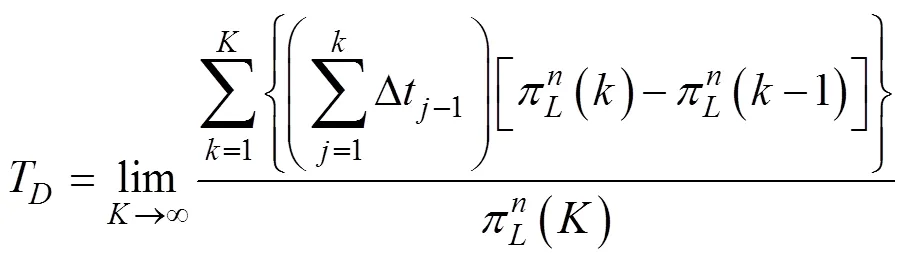
使用类似的方法来评估平均航迹保持时间。跟踪逻辑状态的概率转移矩阵(错过3个检测则终止跟踪)为

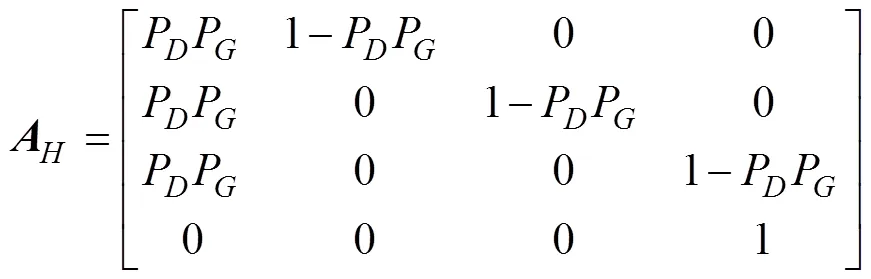
此矩阵指的是状态7, 8, 9, 1。

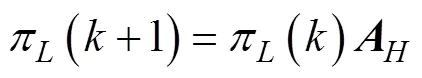
平均跟踪保持时间

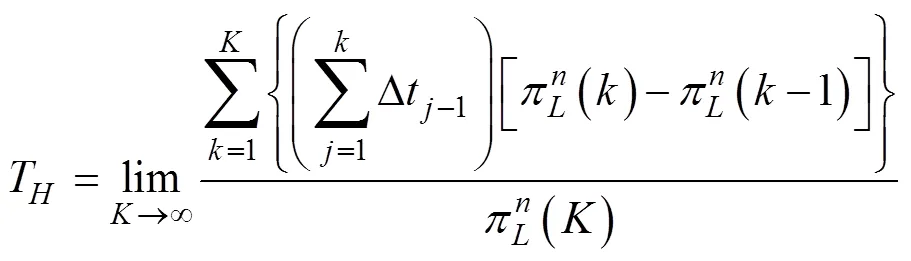
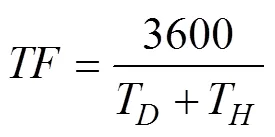
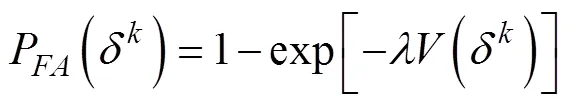
可得

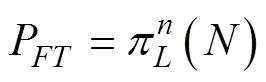
进而得到错误跟踪率

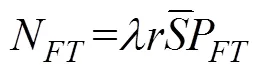
至此, 3个性能指标公式已全部推导出, 跟踪器性能模型已完全建立。可以使用这3个性能指标对跟踪器输出进行评估。

4 数据关联与性能模型的仿真

4.1 最近邻数据关联仿真应用

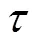
4.2 多假设数据关联仿真应用

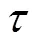
4.3 性能模型仿真

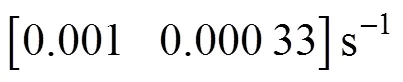
跟踪检测概率是真实跟踪的总持续时间与场景持续时间的比值。对于每一个真实跟踪, 跟踪持续时间是第1个和最后1个接触的时间差。跟踪碎片是跟踪数量与目标数量的比值。错误跟踪率是错误跟踪数量和场景持续时间的比值。

经过100次蒙特卡洛仿真, 最终得到2种数据关联情况下的性能指标如表1所示。

跟踪检测概率越大说明跟踪时间越长, 跟踪碎片和错误跟踪率越小说明错误跟踪越少, 因此,从以上3个性能指标可以看出, 使用多假设数据关联的跟踪器输出质量明显优于使用最近邻数据关联的跟踪器输出质量。

表1 2种数据关联方法的性能指标

4 结论

文中主要探讨了多基地声呐融合探测中的3个关键技术: 测量模型、数据关联和跟踪器性能模型, 得到以下结论。

1) 建立测量模型的目的是综合各种误差对定位带来的影响, 误差越小, 算法越能更好地进行数据融合和目标跟踪。文中出现的定位表达式除了应用于数据融合和目标跟踪算法之外, 还可以应用于传感器布局研究、检验各种多基地移动或固定配置的定位精度、检验对跟踪性能的影响等方面。

2) 数据关联用来确定测量来源, 数据关联配合跟踪逻辑和非线性滤波器可以更好地进行跟踪。数据关联方法中, 最近邻数据关联是一种局部最优算法, 其局限性使其适用于信噪比高, 目标密度小的情况, 而在多目标情况下容易产生错误的关联; 多假设数据关联使用多次扫描延迟决策, 可以有效解决数据关联冲突问题。因此, 须针对不同情况选择合适的数据关联方法。

3) 建立跟踪器性能模型, 从跟踪检测概率、跟踪碎片、错误跟踪率3个性能指标评估跟踪器输出的质量。文中的跟踪器性能模型是基于每个传感器的数据速率相同展开的, 以后可以扩展到不同传感器数据速率的场景。

[1] 徐菲. 双/多基地声呐及其研究概况[J]. 科技广场, 2017(8): 73-77. Xu Fei. Introduction on Bistatic/Multistatic Sonar and its Research Survey[J]. Science Mosaic, 2017(8): 73-77.

[2] 邹吉武. 多基地声呐关键技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.

[3] Coraluppi S. Multistatic Sonar Localization[J]. IEEE Journal of Oceanic Engineering, 2006, 31(4): 964-974.

[4] Coraluppi S, Carthel C. Distributed Tracking in Multistatic Sonar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(3): 1138-1147.

[5] Coraluppi S. Performance Model for Distributed Sonar Tracking[J]. Capabilities of Acoustics in Air-Ground and Maritime Reconnaissance, Target Classification and Identification.RTO-MP-SET-079:37-1-37-11.

[6] Singer R A, Stein J J. An Optimal Tracking Filter for Processing Sensor Data of Imprecisely Origin in Surveillance Systems[C]//Proceedings of the 1971 IEEE Conference on Decision and Control. Miami Beach: IEEE, 1971: 171-175.

[7] Singer R A, Sea R G, Housewright K B. Derivation and Evaluation of Improved Tracking Filters for Use in Dense Multi-Target Environments[J]. IEEE Transactions Information Theory, 1974, 20(7): 201-211.

[8] Bar-Shalom Y, Jaffer A G. Adaptive Nonlinear Filtering for Tracking with Measurements of Uncertain[C]//Pro- ceedings of the 11thIEEE Conference on Decision and Control, New Orleans, Louisiana, USA: IEEE, 1972: 243- 247.

[9] Reid D B. An Algorithm for Tracking Multiple Targets[J]. IEEE Transactions on Automatic Control, 1979, 24(6): 843-854.

[10] Coraluppi S, Grimmett D. Multistatic Sonar Tracking[C]// Proceedings of SPIE Conference on Signal Processing, Sensor Fusion, and Target Recognition Ⅻ, Orlando, FL: SPIE, 2003: 399-410.

Key Technologies of Multistatic Sonar Fusion Detection

ZHANG Hao-yu1, HAN Yi-na1, ZHAO Wei-kang1, YANG Yi-xin1, LIU Qing-yu2

(1. School of Marine and Technology, Northwestern Polytechnical University, Xi′an 710068, China; 2. Naval Research Academy, Beijing 100073, China)

To solve the fusion detection problem for multistatic sonar, this paper discusses three key technologies, i.e., measurement model, data association, and tracker performance model. The measurement model includes the error distributions of time, azimuth, position and sound velocity, as well as the localization expression of a target. The expression of each error factor and the expression of localization error are given. Data association is an important part of fusion detection to solve the assignment problem between measurements and known targets. The methods of nearest neighbor data association and multiple hypothesis data association are introduced in detail. The two data association methods use the same data model, measurement model and motion model. Simulations on the nearest neighbor data association and multiple hypothesis data association show that the target can be well tracked. The tracker performance model is used to evaluate the output quality of the tracker. The output quality is evaluated according to three performance parameters, i.e., tracking probability of detection, tracking fragmentation, and false alarm rate if tracking. According to the performance parameters from simulation, the output quality of the multiple hypothesis data association tracker is significantly better than that of the nearest neighbor data association tracker.

multistatic sonar; measurement model; data association; tracker performance model

TJ630.34; TB566; TP181

A

2096-3920(2018)05-0456-9

10.11993/j.issn.2096-3920.2018.05.013

2018-08-06;

2018-09-29.

国家重点研发计划(2016YFC1400200), 国家自然科学基金面上项目(61671388).

张浩宇(1995-), 男, 在读硕士, 主要研究方向为多基地融合跟踪.

张浩宇, 韩一娜, 赵伟康, 等. 多基地声呐融合探测关键技术研究[J]. 水下无人系统学报, 2018, 26(5): 456-464.

(责任编辑: 陈 曦)