变式思维与创新教学在运动学中的应用与思考

李胜强

(江苏省郑集高级中学城区校区 221116)

高中物理课堂应遵循传统教学内容和教学方法，在知识、能力、思维等方面培养学生的潜能，在课堂教学中应循序渐进的设置台阶让学生渐入佳境，变式训练和变式思维是深化学习能力和效果的法宝，仅以运动学为例谈谈变式思维的应用.

一、关于运动学规律的变式思维与创新教学

例题1 汽车以20 m/s的速度在平直公路上行驶，急刹车时的加速度大小为5 m/s2，则自驾驶员急踩刹车开始，2 s与3 s时汽车的位移之比为____.

变式1 汽车以20 m/s的速度在平直公路上行驶，急刹车时的加速度大小为5 m/s2，则自驾驶员急踩刹车开始，2 s与4 s时汽车的位移之比为____.

变式2 汽车以20 m/s的速度在平直公路上行驶，急刹车时的加速度大小为5 m/s2，则自驾驶员急踩刹车开始，2 s与6 s时汽车的位移之比为____.

变式3 某一质点做匀减速直线运动，其速度随时间的变化关系式为v=20-5t，v与t的单位分别是m/s与s，则2s与6s时质点的位移之比为____.

对比分析例题1考查汽车的刹车运动模型，由题意可得汽车4 s后停下来，刹车的4 s内每1 s的位移之比依次为7：5：3：1，故2s与3 s时汽车的位移之比为12：15即4：5.变式1中的习题解答可沿用例题1的思路，故2s与4 s时汽车的位移之比为12：16即3：4，也可以将4 s分为两部分，故2s与4 s时汽车的位移之比为3：4.变式2中的习题解答时要关注刹车的有效时间，2 s与6 s时汽车的位移之比与2 s与4 s时汽车的位移之比是相同的.变式3中的习题解答时要关注质点做匀减速直线运动的理解，v=20-5t表明质点4 s末速度刚好为零，但此后质点将反向加速运动，2 s与6 s时质点的位移之比与2 s与4 s时汽车的位移之比是不同的，此时可结合v-t求解，2 s与6 s时质点的位移之比1：1.综上所述，对于减速运动应考虑减速运动时间的有效性以及运动的往返性.

图1

例题2 一物体做匀变速直线运动，在连续相等的两个时间间隔内，通过的位移分别是24 m和64 m，每一个时间间隔为4 s，求物体的初速度和加速度，如图1.

解法一基本公式法(一)

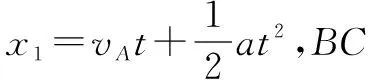
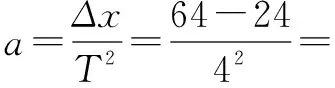
变式1 一物体做匀变速直线运动，在连续两个不同时间间隔内，通过的位移分别是24 m和64 m，时间间隔分别为4 s和8s，求物体的初速度和加速度.

变式2 一物体做匀变速直线运动，通过两个连续相等的位移所需要的时间间隔分别为4 s和6s，已知连续相等的位移为24m，求物体的初速度和加速度.

图2

对比分析关于例题的解答提供了四种方法，解法一和解法二均属于基本公式法，解法三主要是平均速度法，解法四主要是逐差法，四种方法各具特色，解法四更快速灵活一些.变式1提供的情景，时间间隔不同，位移也不同，故不满足逐差法，此题解法四不适用，只能选用前三种解法求解，解法三更好一些.变式2提供的情景，时间间隔不同，但位移相同，也不满足逐差法，故此题解法四也不适用，只能选用前三种解法求解，解法三更好一些.例题是常规习题，可训练学生的发散思维，变式1和变式2通过不同情景的对比，强化学生对时间间隔和位移的对应关系的理解，尤其是强化理解Δx=aT2的使用条件，通过一题多解和一题多变，加强学生思维的灵活性和深邃性的培养.

二、关于运动学图像的变式思维与创新教学

例题3 一质点做匀变速直线运动的v-t关系图像如图2所示，则该质点的x-t关系图像可大致表示为图3中的( ).

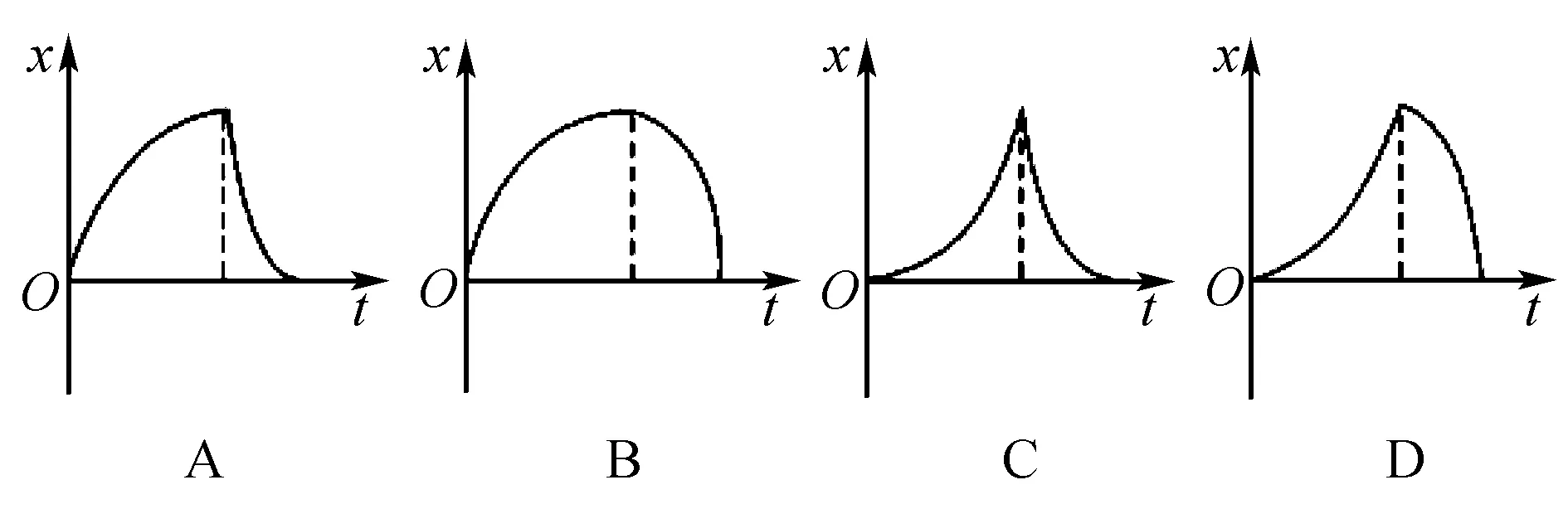
图3

图4

变式1 如图4所示，图线A和图线B分别为A、B两物体的v2与x的变化规律.

(1)尝试分析A、B两物体的初速度和加速度

(2)假设A、B两物体在t=0时刻处在同一位置，求B物体经过多长时间追上A物体？

图5

变式2 如图5所示，图线为某物体的v与x的变化规律，图线为顶点在坐标原点，开口向右的一条抛物线，尝试分析物体的运动性质

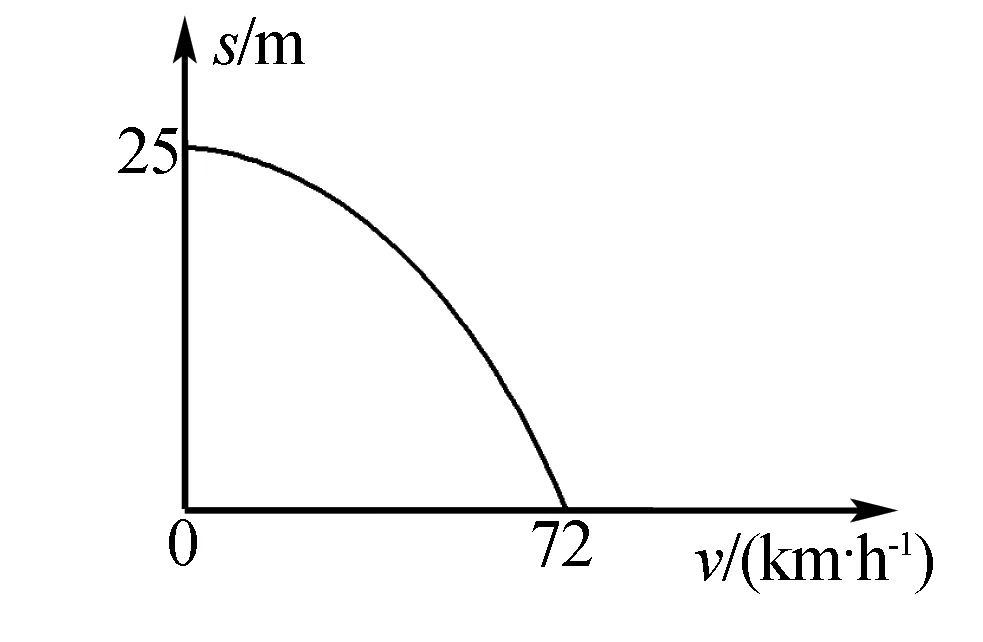
图6

变式3 汽车减速过程中的位移s与速度v的关系曲线如图6所示，减速过程过程可视为匀变速直线运动，计算汽车的加速度.

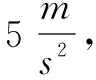
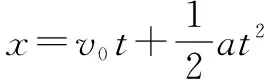
一题多变的目的是通过对习题的情景或问题的呈现方式的变化，强化对物理原始问题的分析，以不变应万变.一题多解的目的则是从不同角度解决同一类习题，强化思维的发散性和解题方法的技巧性.