与向量有关问题的解法探究

闫大森

(河北省衡水第一中学 053000)

向量是近代数学中重要和基本的数学概念之一，它是沟通代数，几何与三角函数的一种工具，有着极其丰富的实际背景，但是在解题中人们常常忽视对其形式的变通，从而轻视了它的可贵价值，事实上，正是由于向量具有代数与几何形式的双重身份，它有着极其丰富的实际背景，在解题中具有独特的功能.

一、向量在数列问题中的应用

例1 已知数列|an|是公差d≠0的等差数列，记Sn为其前n项和.

(1)若a2，a3，a6依次成等比数列，求其公比q；

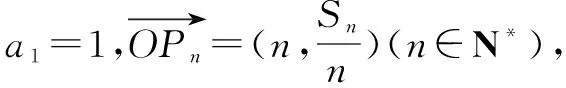
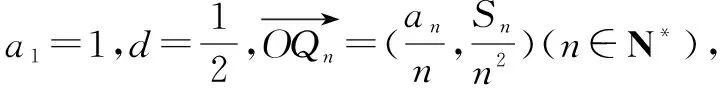
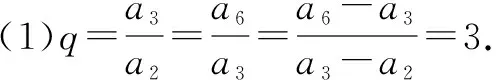
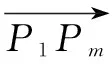
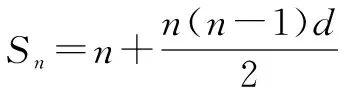
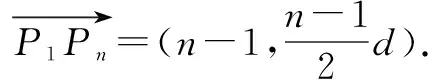
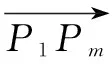
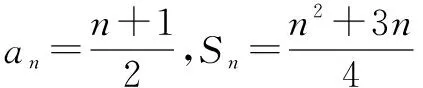
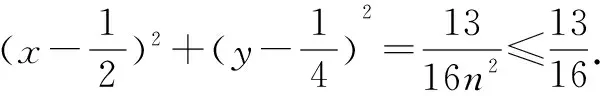
点评这类问题主要是运用平面向量的模，数量积等相关知识，实现形到数的转化，巧妙地将平面向量、数列等知识融合在一起，重点考查平面向量、数列的“三基”.

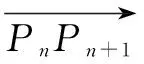
(1)求xn的表达式；

(2)确定n的值，使点Pn在直线x-ny= 0的下方，并加以证明．

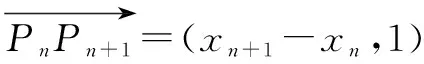
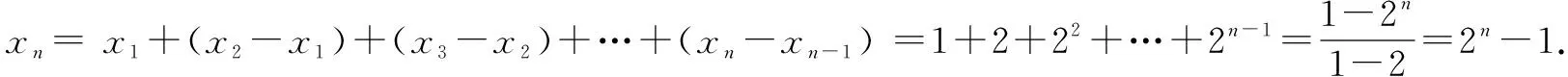
上式对n=1时也成立，即xn=2n-1．

(2)点Pn在直线x-ny= 0的下方的充要条件是2n-1-n2>0，即2n>n2+1．

当n=1，2，3，4时，不等式2n>n2+1不成立．

当n≥5时，

因此，n的取值为n≥5，n∈N*．

评析本题将向量、数列、不等式以及二项式定理联系在一起，体现了在知识交汇点处设计数学考题的思想，特别是用二项式定理证明不等式的技巧得到了充分展示，考查了对知识综合运用的能力．平面向量的知识与其他有关知识得到了很好的整合，是典型的交汇热点试题．

二、平面向量在三角函数中的应用

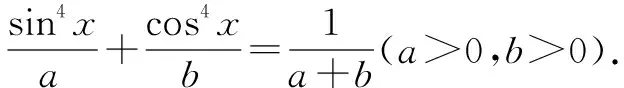
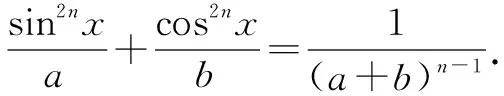
分析借助向量不等式|a·b|≤|a||b|等号成立的条件，构造向量，可化难为易.

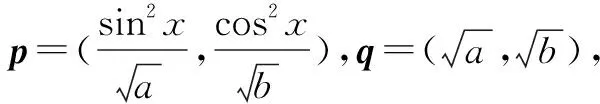
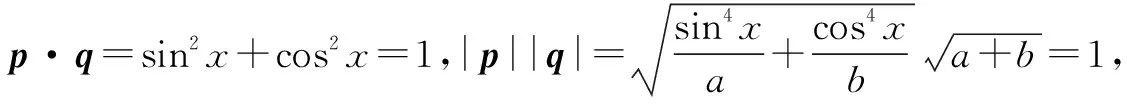
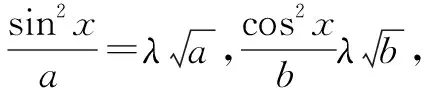
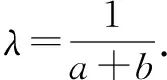
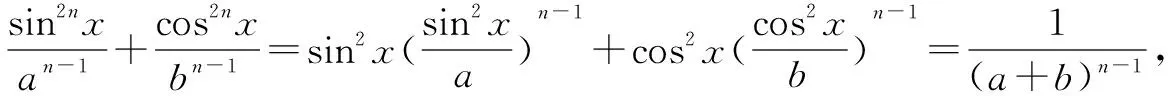
点评本题利用向量不等式|a·b|≤|a||b|等号成立的条件，成功地将三角恒等式的证明转化为向量问题，证法简洁流畅，利用平面向量的概念和坐标运算，将三角函数问题向量化，体现了“向量问题函数化、函数问题向量化”的等价转化思想，其中模的平方与向量数量积之间的关系|a|2=a·a=x2+y2，a=(x，y)是向量和实数互化的依据和桥梁，也是重要的转化方法.