分析函数的单调性在高中数学中的学习与应用

史 赢

(江苏省南京市文枢高级中学 210000)

一、函数单调性的基本概念及其作用

1.函数单调性的基本概念

一般来讲设函数f(x)的定义域为I.在I内的某个区间当中，对于两个任意的自变量x1、x2，如果x1f(x2),那么就说f(x)在这个区间上是减函数.

单调性与单调区间则是：若函数y=f(x)在某个区间是增、减函数,则就说函数在这一区间具有(严格的)单调性,这一区间叫做函数的单调区间.此时该函数是这一区间上的单调函数.

2.函数单调性的作用分析

高中数学知识当中，函数类的知识无论是一次函数或是二次函数都有涉猎.认识到高中函数的增加、减少的内容之后，学生在学习或解答问题阶段必然要从基础的知识内容开始.将数学的符号或例题进行解析，从而全面了解函数单调性的基本概念.函数单调性是以一种变量的形式存在，并作为函数学习的重点部分.通过课本中的知识内容陈列，将函数作为一个独立的单元，要求学生通过图象、文字等进行融合，从而将其理解和认识把控到位.学生在今后学习高中的不等式或是导数等数学知识都会以此为基础，开展下一个阶段的学习和研究方向.

二、函数单调性在高中数学中的学习以及应用探究

1.求值域

2.求导数

先了解函数导数的基本定义，才能在函数单调性解决数学问题阶段高效的运用.高中数学问题当中复杂的参数函数以及高层次的函数问题相对来讲比较多，学生通过对导数定义明晰之后，能够利用函数单调性的知识快速解决数学问题.函数求导阶段首先要将问题中，函数的单调性进行判断，找出函数的单调区间.那么求导阶段将关系式或表达式进行转变，从而将能够快速地找到其定义域的单调区间.通过假设和论证最终能够将函数的增减性判断出来，得出导数在函数单调性当中的重要作用，并能将单调性的指示性能合理利用，这对于高中生来说也是明确解决问题的基本思路的有效过程.

3.解数列

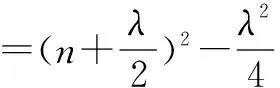
故答案为(-3，+∞).

4.解方程

5.解不等式

高中阶段的数学学习离不开学生对基础定义与计算公式的记忆，但并不是每一位同学都能进行知识结构建立和总结，进而在解题过程中最大可能减少失误问题的产生.教师引导学生利用函数的单调性解答数学不等式，通过将不等式进行分类或换元的解答方式，从而能够精准地找出相关问题的结果，学生的数学思维和能力也在这个过程中得以培养和巩固，对之后的数学知识学习大有裨益.

高中阶段函数的单调性知识对学生的数学成绩和能力的影响较大.为了保证之后的学习有基础知识作为依据，学生能够在期中、期末甚至高考当中将自己的能力和水平体现出来.高中数学教师应该重视函数单调性在学习和解题运用中的方法进行研究和分析，并要求学生通过训练和模拟将这部分知识掌握.教师带领学生对数学问题进行探究，继而能够将数学中的不等式、方程、求值域、数列等相关数学知识和问题解答，使得学生在这个过程当中，培养自己的数学思维，并建立起数学知识结构和体系，保证数学能力处于一个持续提升的过程当中，为自己的未来做好充分的准备.