高分辨率遥感影像道路频谱特征分析

卫霄芳， 况润元， 赵艳福

（江西理工大学建筑与测绘工程学院，江西 赣州341000）

0 引 言

道路作为城市的骨架，是城市空间信息的重要组成部分，道路信息的实时更新对于导航，交通管理等实际应用具有重要意义.随着卫星遥感技术的发展，越来越多的高分辨率遥感影像得到广泛应用，高分辨率遥感影像大量涌现[1].我国正迎来自主卫星为主的高分时代[2].人们经过多年探索和研究，已经发展了一系列根据像元光谱能量的差异进行地物识别和分析的思路和方法，并且已经广泛应用于许多领域[3-5].如今遥感技术已经可以实现大面积实时或准实时高分辨率遥感影像的获取，为用户提供光谱、纹理、空间结构特征更加丰富的地物信息.但是在空间域中这些信息往往纠缠在一起，很难将它们分离开来[6].长期以来，遥感影像特征提取主要采用基于像元的方法，这种方法是根据地物的光谱特征对地物进行提取或分类的，即同种光谱特征的像元聚集在同一特征区域.但是即使是高分辨率遥感影像，也无法避免“同物异谱”和“异物同谱”的情况.从道路角度分析，对于有阴影、行道树遮盖、高大建筑物遮盖等情况的道路，即使采用高空间分辨率遥感影像也基本无法通过光谱特性进行识别和分类.

国内外研究发现，地物不仅可以通过发射和反射电磁波谱的能量来表征自己，还可以通过自身具有的空间频率谱能量来表征自己，并且依据Parseval定理，特定基元内的电磁波谱能量和空间频率谱能量是相等的[7].要想提高遥感数据处理的精度，就要提高综合运用多种遥感信息的能力，寻求新的理论支持和定量化、精确化算法[8].地物的纹理、结构和细部特征，与地物的空间频率相关，充分利用空间频率对信息分析、解译地物具有重要意义[9].电磁波谱特性反映了基元内子像元的整体波谱特征，空间频率谱特性则反映了基元内子像元能量不同频率的分布特征，恰好和地物的色调、结构、纹理等特性存在密切联系[10-11].研究表明，对“异物同谱”的基元进行分析时，在光谱特征和统计特征一致的情况下，当频谱特征有差异时，也可进行区分[12].适当的频域增强可以使影像的目标特征更清晰，更易于辨识[13].对于图像中的道路对象，其频域表征可以将其几何纹理、空间结构等有效信息与光谱信息分离开来，分析道路在频域中的单纯空间几何特征，对于图像中道路特征增强和道路提取具有重要意义.因此考虑从高空间分辨率遥感影像的频谱特征入手，利用专业影像处理工具IDL对道路特征在幅度谱中频率的径向和角向能量分布进行分析，获取道路的空间特征，为道路的线状特性滤波及道路的快速准确提取提供依据.

1 研究数据

文中所使用的高分辨率遥感影像为2012年9月16日获取的IKONOS赣州市一景遥感影像，包含4个多光谱波段和1个全色波段，图像成像质量较好，基本无云层覆盖，融合后的空间分辨率为0.8m.在其中裁剪4幅具有代表性，大小均为250×200像元的影像T1～T4作为实验对象，见图1.

其中，T1图像包含一条道路特征明显的近似理想道路以及一些水体，属城市道路中的次干路；T2图像主要包含沿道路分布的行道树和一些不规则分布的建筑物，道路特征部分被掩盖，属城市道路中的支干路；T3图像主要包括沿路分布的行道树、规则和不规则分布的建筑物，道路特征完全被遮挡，属城市道路中的支路，T4图像主要包含一些高大建筑物、建筑物阴影及一些水体，道路特征大部分被遮挡，属城市道路中的支路.

图1 实验影像T1～T4

2 研究方法

2.1 傅里叶变换

在数据的频谱分析中，最基本的数学工具就是傅里叶变换(FFT).对图像来讲，一维信号研究的是时域和频域的问题，二维图像研究的便是空域和频域的问题.这一工具架起了二维图像空域与频域之间的桥梁.二维离散傅里叶变换对的数学公式为：

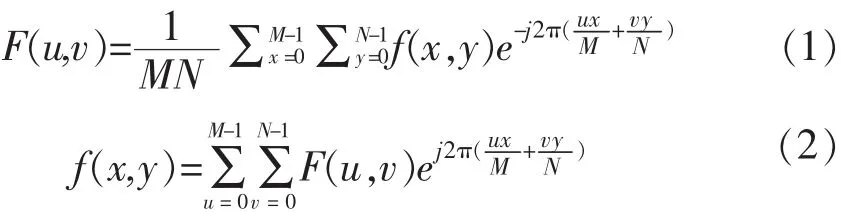
其中，M和N为图像大小，x和y为图像的空间坐标，u和v分别为x和y方向的空间频域分量.

一般情况下，f（x,y）通常为实函数，其傅里叶变换 F（u,v）通常为复函数.若 F（u,v）的实部为 R（u,v），虚部为 I（u,v），那么其复数形式和指数形式可表示如下：

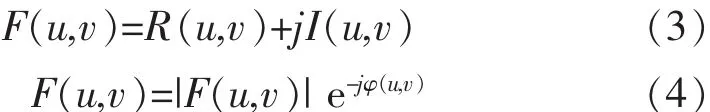
其中，

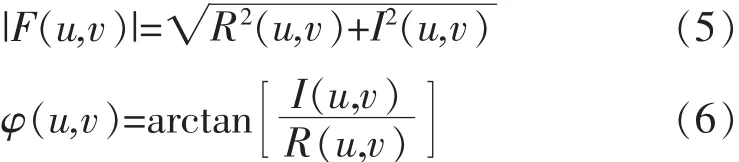
|F（u,v）|为图像经傅里叶变换对应的幅度谱，即频谱；φ（u,v）为图像经傅里叶变换对应的相位谱.一般情况下，频谱决定了图像种各频率分量的多少，相位谱决定了各频率分量在图像中的位置.幅度谱中能量的变化影响的是图像灰度大小的变化，而相位谱的变化可能会对图像呈现的完整性造成影响，因此我们通常只对幅度谱进行处理.

利用IDL中的read_tiff函数对影像进行读取时，与一般图像以左上角为原点不同，IDL中图像则是以左下角为原点，因此呈现的影像会是上下颠倒的，这一点不会受该影像的orientation信息的影响.文中所用影像的orientation值为1，即第0列在最左侧，第0行在顶部.为了将影像按原始影像的orientation信息显示，并且方便下一步的傅里叶变换，需要提取TIFF文件的其中一个波段，并用rotation函数进行原图显示，原图orientation值为1，对应的rotation函数中的direction应为7.

文中采用IDL自带的快速傅里叶变换（FFT）将图像由空域转化至频域，并利用关键字 “/center”将低频分量移至频谱图中心位置，以便对频谱图的视觉分析.同时，为了使频谱图中道路特征更明显，在显示时对其进行取对数处理，效果见图2.为了更直观的呈现频谱的分布情况还可以利用surface函数对幅度谱进行三维显示，效果见图3.

图2 实验影像T1～T4频谱能量图

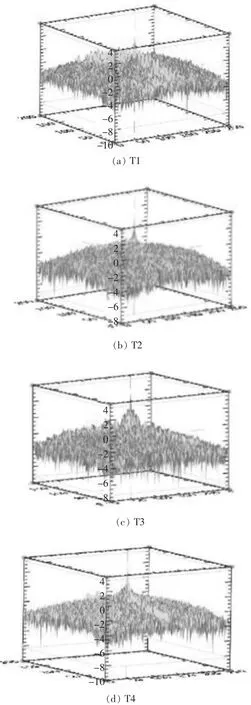
图3 实验影像T1～T4频谱能量曲面图

对4幅影像能量谱平面图和三维曲面进行视觉定性分析，并与空域影像进行对比，T1影像有一条亮度突出的谱线，方向与空间域道路恰好垂直；T2影像频谱能量中的亮线虽不如T1明显，但依然可以判断出大致方向，与空间域道路方向垂直；T3影像频谱能量图亮线非常清晰，但有可能对该方向贡献较多的会是沿道路规则布设的建筑物边线；T4影像频谱能量图中亮线不太明显，从视觉上无法判断哪个方向或哪个圆周上谐波分布更为多，这是因为在空域影像中T4的道路或道路周围的地物均未呈现出较明显的线状特征，有待进一步的定量分析.

具体实现过程如下：

;读取原始影像

file=filepath（'T1.TIF',root_dir=['c:'],$

subdirectory =['Users','Administrator','desktop']）

img0=Read_tiff（file）

;提取其中一个波段

img1=img0[2,*,*]

img1=reform（img1）

img1=rotate（img1,7）

img01=image（img1,window_title='redband'）;傅里叶变换

ffTransform=FFT（img1,/CENTER）

powerSpectrum=ABS（ffTransform）^2

s=powerSpectrum

img03=IMAGE（ALOG10（s）,$

window_title='powerspect'） ;能量谱

sur=SURFACE（ALOG10（s）,$

COLOR='aquamarine',$

AXIS_STYLE=2） ;能量谱的三维显示

2.2 频谱能量信息特征分析

为了定量分析遥感影像频谱能量信息表征，分析空域道路特征与频域能量谱线之间的关系，最直观的方法是沿一条直线直接做频谱图的剖面线，但这种方法只能反映所选定直线上的能量变化，无法反映图像的全局幅度变化特征.因此考虑将图像频谱能量分析与数学统计分析相结合.最早考虑这种方法的是Conners和Harlow（1980），他们提出了环状采样和楔状采样的方法，即以频谱中心为原点，分别以同心圆环和扇面为母体向四周作辐射状扫描，求出环形区域内和一定扇形区域内各次谐波的能量总和，从而得出频谱能量分布的径向特征和角向特征.

基于此，采用可以反映图像全局径向和角向分布特征的方法进行分析,即以频谱中心为原点，以同心圆和直线的形式向四周作辐射状扫描，得出一定半径r的圆周上和一定角度θ的直线上的各次谐波的总和.在频谱图中，如果以图像中心为原点（0,0），则在半径r上对应的是图像中空间频率相同但方向不同的频率点，而在角度θ上对应的是图像中方向相同但空间频率不同的频率点[14].

1）径向分析

基于IDL平台对频谱图进行径向能量分析的主要思路是：找到频谱图的中心位置（x0,y0）；以（x0,y0）为原点，定位r=0,1，…，rmax的圆周上的所有频率点，其中rmax为圆周半径可能的最大值，在该实验中rmax为100像元；对所定位的所有频率点对应的幅度值求和；最终获得频谱图幅度值随半径增大的变化情况.由于幅度值随半径增大迅速衰减，为了使变化趋势更明显，对半径r进行对数显示.显然，获取径向分析所需频率点在极坐标中更容易实现，而IDL中图像存储是按行排列的，因此需要建立极坐标点与对应像元索引值之间的变换关系.

具体实现过程如下：si=size（s）

x0=ceil（si（1）/2）y0=ceil（si（2）/2）

N=floor（min（[si（1）,si（2）]））

rmax=floor（min（[si（1）/2,si（2）/2]））

srad=fltarr（rmax）

srad（0） =s（x0,y0）

angle=[91:270]

for r=1,rmax-1 do begin

r_=r+intarr（180）

rect_coord1=cv_coord（from_polar=[transpose（angle）,transpose（r_）],$

/to_rect,/degrees）

rect1=round（rect_coord1）

x=rect1[0,*]

y=rect1[1,*]

x=x0+x

y=y0+y

index1=[x,y]

arr=intarr（n_elements（x））

for i=0,n_elements（x）-1 do begin

arr（i）=array_indices_reverse（s,index1[*,i]）endfor

srad（r）=total（s[arr[uniq（arr[sort（arr）]）]]）endfor

r=[0:rmax-2]graph1=plot（alog（r）,srad（r）/10^4,title='径向分布曲线',$

xtitle='半径的对数 ',ytitle='幅度值/10^4',xrange=[0,rmax-1]）

以上过程中用到的array_indices_reverse函数是array_indices函数的反函数.它可以将指定数组中某个或某些值对应的坐标值转化为索引值，具体函数如下：

function array_indices_reverse,array,indexArr,DIMENSIONS=dimensions

compile_opt idl2

ON_ERROR,2

if（N_PARAMS（） ne 2） then$

MESSAGE,'Incorrect number of arguments.'

arrDims=size（array,/dimen）

idxNum=N_Elements（indexArr）

if idxNum GT 1 then return,long（indexArr[idxNum-1]*$

product（arrDims[0:idxNum-2]）+$

array_indices_reverse（array,indexArr[0:idxNum-2]））$

else return,indexArr

end

实验结果如图4所示，从图4中可以看出幅度值分布基本集中在频谱图的中心处，即低频位置，高频能量的贡献则很少，随着半径的增加，即频率的增大，幅度值迅速衰减，从中无法提取出其他有利于道路特征识别的信息.

2）角向分析

理论上讲，方向特征是道路在空域的一个显著特征，其在频域上的表现为在某个方向上能量值较大，因此角向能量分布特征的研究是至关重要的.由于频谱图的对称性，角向能量分布的分析通常选取半周范围内能量随角度的变化情况即可，为了便于IDL的运算，文中选取的角度范围是[91°，270°].

在IDL中实现思路为：找到频谱图的中心位置（x0,y0）；定位[91°，270°]范围内以 rmax 为半径的所有频率点；分别计算每个角度所在直线上对应的所有频率点的能量值并求和.

具体实现过程如下：

rmax_=rmax+intarr（180）

rect_coord2=cv_coord（from_polar=[transpose（angle）,$

transpose（rmax_）],/to_rect,/degrees）

rect2=round（rect_coord2）

x=rect2[0,*]

y=rect2[1,*]

x=x0+x

y=y0+y

sang=fltarr（n_elements（x））

for an=0,n_elements（x）-1 do begin

vx=abs（x（an）-x0）

vy=abs（y（an）-y0）

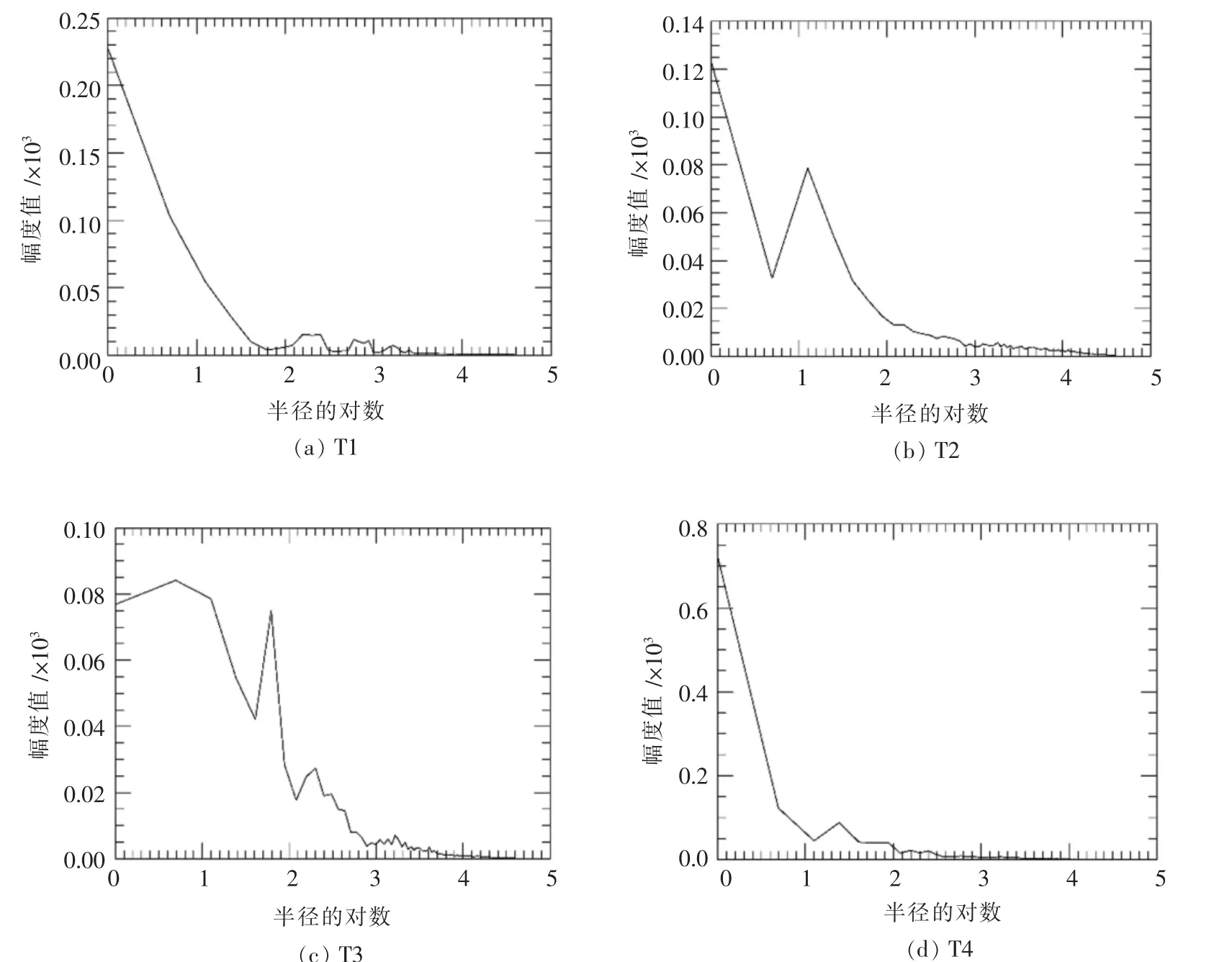
图4 实验影像T1-T4频谱径向分布曲线

if（vx eq 0） and （vy eq 0） then begin

vx=x0

vy=y0

endif else begin

m= （y（an）-y0）/（x（an）-x0）

xr=transpose（[x0:x（an）]）

yr=round（y0+m*（xr-x0））

endelse

index2=[xr,yr]

arr2=intarr（n_elements（xr））

for i=0,n_elements（xr）-1 do begin

arr2（i） =array_indices_reverse（s,index2

[*,i]）

endfor

sang （an）=total （s[arr2[uniq （arr2[sort（arr2）]）]]）

endfor

an=[0:n_elements（x）-1]graph2=plot（angle,sang（an）/10^6,title='角向分布曲线',$

xtitle='角 度/度 ',ytitle='幅 度 值/10^6',xrange=[91,270]）

实验结果如图5所示.从图5中可以看出，T2～T4频谱角向分布的峰值在一定角度内保持不变，这是因为在IDL中对半周进行运算时，跨越了180°，而最外周经过的频率点有200个，难免会出现不同角度对应的频率点相同的情况，故而导致能量值重复.此外亮线 （即频率分布较集中的地方）跨越角度范围大致在10度左右，这也是导致峰值在一定角度内保持恒值的原因之一，但是对于获取道路的方向信息并不影响，因为峰值方向代表的就是道路和一部分与道路方向相同的的方向信息，这些都是对识别或增强道路有利的信息.

T1影像在106°左右出现频谱能量统计最大值，显然这一方向上的能量正是由道路提供的；T2影像在230°至240°左右出现最大值，这一方向信息大部分是由道路提供，也有部分是由下方与道路方向平行的规则建筑物提供，在252°左右有一个小的峰值，是由道路上方与道路有一定夹角的建筑物提供的；T3 影像在 120°～130°出现最大峰值，因为影像中道路为支路，且行道树较茂盛，空域影像中基本无法判断并提取道路，但沿路规则分布的建筑物也指示了道路的存在，在频域图中这个方向信息更加明显；T4影像在120°～130°出现最大峰值，与空域图对比发现与道路方向垂直.

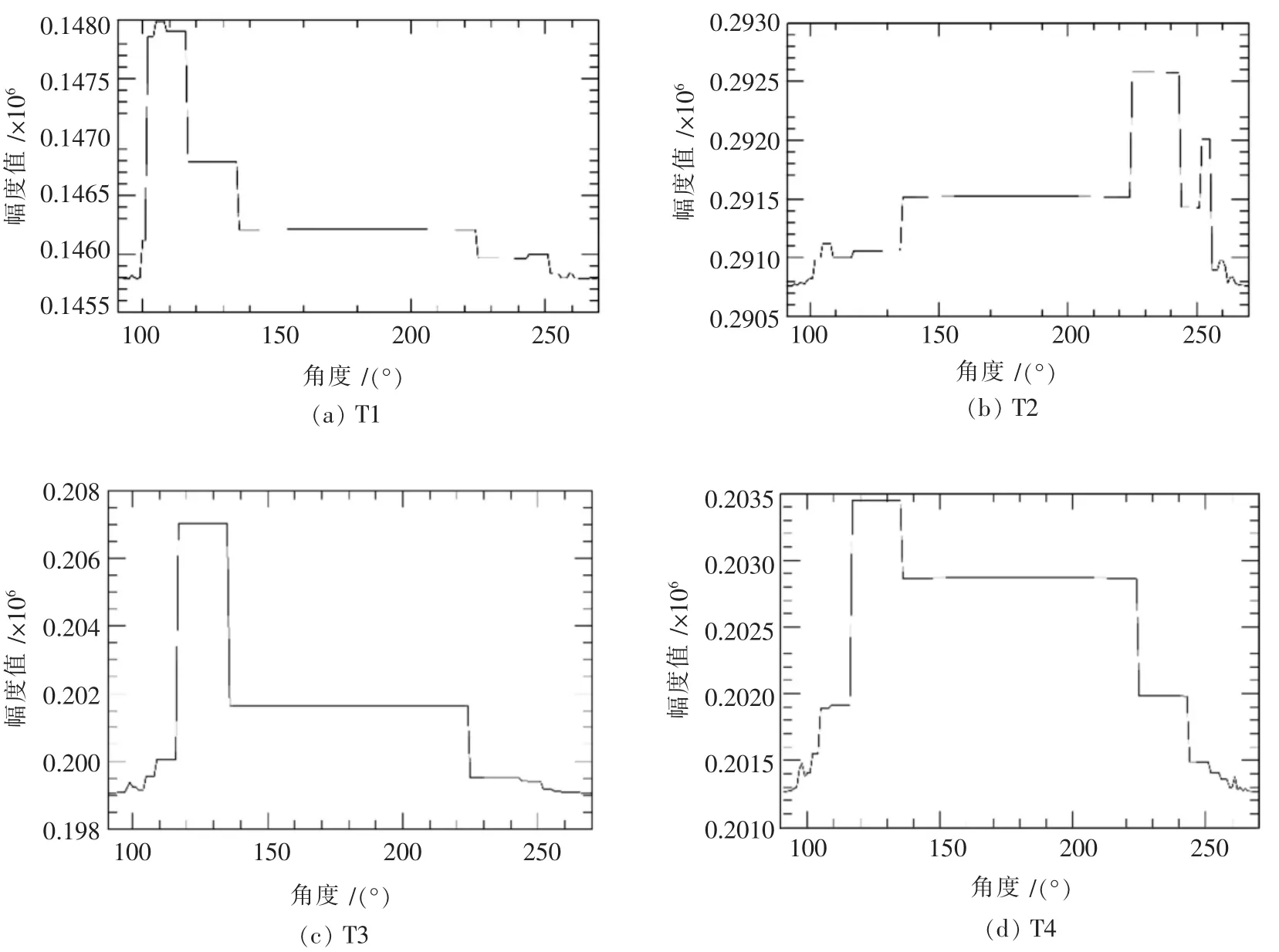
图5 实验影像T1～T4频谱角向分布曲线

通过对4种典型道路图像的频谱角向能量分析发现，空域下不论是何种道路均可以通过影像中的上下文信息准确判断出道路的方向特征，这种突出的方向特征是道路独有的.即使在道路线性方向特征不太明显的影像上，也可以通过频谱的角向能量分布准确判断道路的方向特征信息，这就说明影像频谱的分析可以为高分辨率遥感影像中道路准确快速提取提供新的思路.

3 实验结果分析

文中从赣州市选取4幅空间域提取难度较高的、具有代表性的遥感影像，利用IDL将其经快速傅里叶变换转换至能量保持恒定的频率域，并对频谱图中的幅度谱能量分布进行了径向和角向分析.

从实验结果来看，径向能量分布曲线描述了能量统计值随频率的变化关系，T1～T4能量分布在半径接近零处，即低频位置存在峰值，但未必与道路特征存在相关性；角向能量分布曲线描述了能量值随角度的变化关系，T1～T4能量分布均存在峰值，且方向与道路垂直，其中道路特征最明显的图像T1对应峰值在105°～108°范围内，道路有部分被行树遮盖的影像T2对应峰值在224°～242°范围内，道路完全被行道树遮盖的图像T3对应峰值在118°～137°范围内，道路有部分被建筑物或阴影遮盖的影像T4对应峰值在118°～135°范围内.分析发现建筑物、行道树或阴影可以遮盖道路的光谱信息，但无法掩盖道路或由沿道路规则分布的与道路方向一致的地物所提供的可反映道路方向的信息.道路在频域中的这种独有特性的应用对道路的识别和提取研究具有重要意义.

4 结 论

通过IDL对不同道路提取条件下的遥感影像的频谱能量分布的径向和角向分析，发现了道路的方向特征在影像频率域的优势，即道路方向在空域和频域的视觉表征为相互垂直，且这一特征不受行道树、阴影或建筑物遮盖的影响，这一结论为道路特征的准确识别提取提供了新思路.但研究方法依然有优化和深化的空间，后续的滤波器设计和道路提取方法的选择也还有待进一步探究.需要说明的是，文中所选取的实验数据均为直线型道路，该类型道路方向性特征明显，但是对于方向性特征不明显的弯曲道路、环岛，无法利用该方法进行此类道路的增强.