折射率色散对空间硅太阳电池双层减反射膜反射率的影响
王安祥,李继军
(1.西安工程大学 理学院,陕西 西安 710048;2.内蒙古工业大学 理学院,内蒙古 呼和浩特 010051)
0 引 言
为了提高太阳电池转换效率,通常在太阳电池表面镀减反射膜以减小太阳电池表面对光的反射损失[1-2].许多学者对具有减反射膜的太阳电池表面进行了大量研究,ABDULLAH[3]和LENNIE[4]等设计了应用于硅太阳电池表面的SiO2、Si3N4、ZnO以及ZnS单层减反射膜,并分析单层减反射膜的厚度对电池光电流、转换效率的影响;BOUHAFS等[5]计算了单、双及三层减反射膜硅太阳电池的加权平均反射率,并比较了几种减反射膜硅太阳电池在一定波长范围内反射率的理论计算值和实验测量值;CID等[6]对减反射膜硅太阳电池进行了理论和实验研究;周涛[7]利用传递矩阵法优化设计出多种常见介质膜材料的减反射结构,通过光吸收效果和钝化效果对各种减反射膜性能进行综合评价,得出SiO2/Si3N4减反射膜优于MgF2/ZnS减反膜;刘永生[8]设计了低折射率纳米材料的减反射膜,这种新型纳米减反射膜系所得最小加权平均反射率,与采用常规材料的减反射膜系相比得到明显减少;杨文华[9]通过数值计算给出了单、双及三层减反射膜的最佳膜厚,分析了减反射膜膜层厚度变化对反射率的影响,并对有钝化层的双层减反射膜进行了优化设计.上述减反射膜的研究均没有考虑折射率色散效应,由于发现文献[5-6]中减反射膜的理论计算值与实验数据在短波范围内差别较大,而且上述减反射膜的研究均没有考虑折射率色散效应,将材料的折射率在宽光谱区域看作常数,然而折射率色散效应对减反射膜的反射特性有重要影响,已有学者对材料的折射率色散特性进行了研究,刘华松等[10]利用电子束蒸发在硅基底上制备了TiO2、HfO2、Ta2O5和Y2O34种金属氧化物薄膜的样品,研究了金属氧化物薄膜在中波红外波段内(2.5~5μm)光学常数的色散特性;白一鸣等[11]计算了色散效应对晶体硅太阳电池反射率的影响,并分别将考虑与未考虑色散下2种减反射膜晶体硅太阳电池的反射率数值结果与实验测量数据进行了对比分析,得出考虑折射率色散效应的计算结果与实验测量数据完全相符,而未考虑折射率色散效应的计算结果与实验测量数据差别较大;王安祥等[12]将3种智能算法分别应用于晶体色散方程的参数反演中,获得了石英和方解石晶体的Sellmeier方程的参量;刘华松等[13]研究了在考虑膜层材料折射率色散情况下,周期性结构薄膜反射区中心波长与带宽特性.以上研究得出了色散情形下的一些有用的结论,但是所验证的膜系种类较少,而且在上述减反射膜的验证中没有定量判定计算值与实验值的差别,也没有进一步研究考虑折射率色散效应的膜系设计.
本文将在考虑折射率色散效应的情况下,通过光学干涉矩阵法分别数值计算2种MgF2/ZnS双层减反射膜晶体硅太阳电池的反射率,以验证考虑色散下减反射膜的反射率数值计算结果与实验测量数据是否相符,并利用智能优化算法设计双层减反射膜的硅太阳电池.
1 考虑折射率色散下双层减反射膜的反射率的数值计算
下面分别计算考虑色散与未考虑色散下空间硅太阳能电池的反射率,并与文献所提供的实验数据进行比较,分析折射率色散效应对硅太阳电池反射特性的影响.由于基底硅是弱吸收基底[6],且所研究减反射膜材料的消光系数在紫外、可见光及近红外区域几乎为零,因此,在膜系设计中没有考虑折射率的消光系数.在考虑折射率色散效应时,减反射膜材料和作为基底的晶体硅色散关系都全部考虑,它们的折射率色散关系如图1所示[14-16].在不考虑折射率色散效应时,晶体硅和减反射膜材料折射率取值:MgF2为1.38,SiO2为1.46,ZnS为2.35,Al2O3为1.675,ZnSe为2.42,晶体硅为3.9.
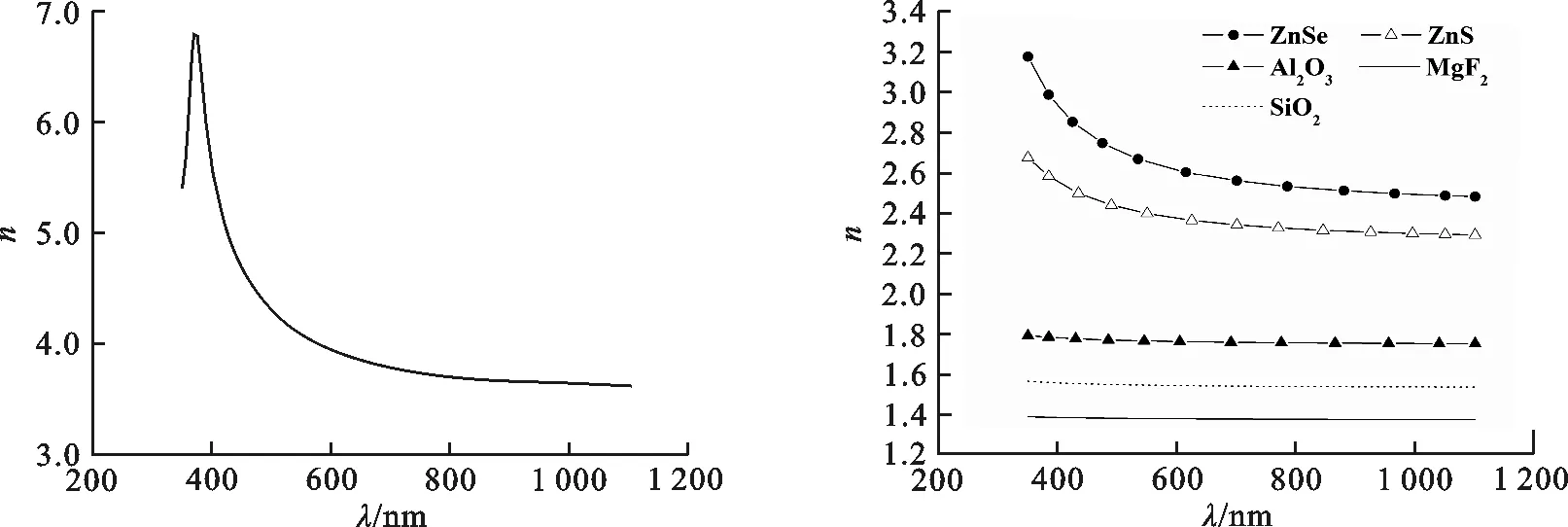
(a) 晶体硅的折射率色散关系 (b) 其他5种减反射膜的折射率色散关系图 1 晶体硅和5种减反射膜材料的折射率色散关系Fig.1 Refractive-index dispersion relationship of crystalline silicon and five anti-reflection coatings
对于多层减反射膜系的反射率,采用导纳矩阵法计算获得[12],膜系的特征矩阵为
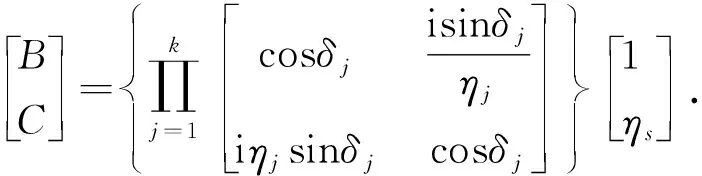
(1)
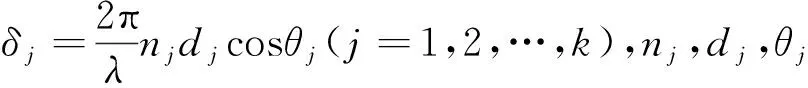
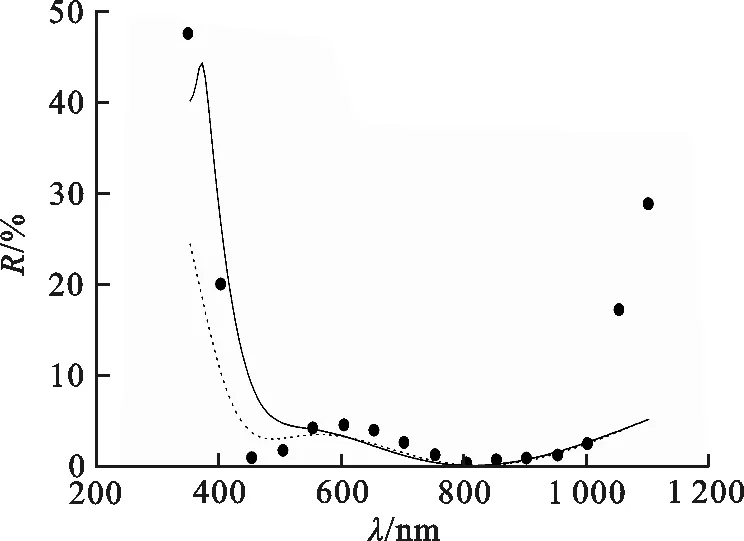
图 2 MgF2(98 nm)/ZnS(70 nm)双层减反射膜晶体硅太阳电池的反射率随波长的变化Fig.2 Variation of the reflectance of crystalline silicon solar cells with a double-layer MgF2(98 nm)/ZnS(70 nm) anti-reflective coating with wavelengths
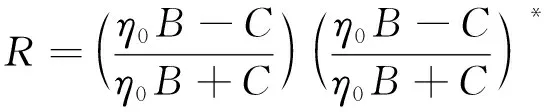
(2)
式中:η0为入射介质的导纳.
将减反射膜硅太阳电池反射率的实验值和数值计算值的差方和s=∑(R-R′)2作为衡量数值计算值与实验值拟合的优劣.式中R′为减反射膜反射率的数值计算值,R为实验测量值,差方和s的取值越小说明拟合效果越好.
1.1 MgF2(98nm)/ZnS(70nm)双层减反射膜的反射率的数值计算
根据文献[6]给出MgF2(98nm)/ZnS(70nm)双层减反射膜晶体硅太阳电池的膜系参量,通过光学干涉矩阵法计算出考虑色散下反射率随波长变化关系,图2中黑点符号和实线分别表示实验数据(文献[6]中图7所示数据)和考虑折射率色散效应的情况,发现考虑色散下反射率的理论计算值与实验数据符合很好.然后,计算出未考虑色散下反射率随波长分布关系,如图2中虚线所示.可以看出,在610~1 100 nm波长范围内,考虑和不考虑折射率色散效应情形下所得反射率差别极小,并且在610~1 000 nm波长范围内均与实验测量数据符合很好;在350~600 nm波长范围内,考虑和不考虑折射率色散效应情形下所得反射率差别明显,但是考虑折射率色散效应情形下的反射率与实验测量数据更吻合,特别在350~370 nm波长范围内,考虑和不考虑折射率色散效应情形下的反射率随波长变化趋势完全相反.经过计算,得到考虑色散与不考虑色散效应下MgF2(98 nm)/ZnS(70 nm)双层减反射膜晶体硅太阳电池反射率的实验值和数值计算值的差方和s分别为3.57×10-2与7.80×10-2,说明考虑折射率色散效应的数值计算结果更与实验测量数据相符.说明一下,文献[6]中MgF2(98 nm)/ZnS(70 nm)双层减反射膜采用电子束沉积,膜厚通过石英晶体监控,ZnS的沉积速率为2~3 Å/s,衬底温度为125 ℃; MgF2的沉积速率为3~5 Å/s,衬底温度为200 ℃.真空室压强为(2~5)×10-3Pa.
1.2 MgF2(104 nm)/ZnS(80 nm)双层减反射膜的反射率的数值计算
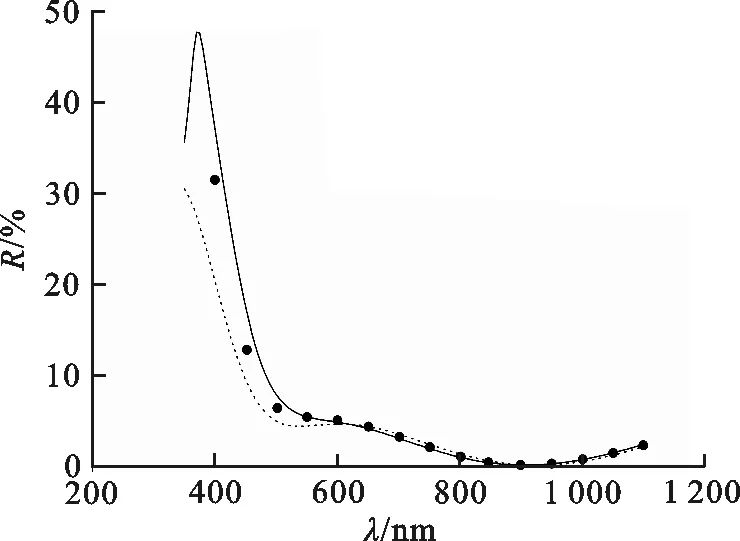
图 3 MgF2(104 nm)/ZnS(80 nm)双层减反射膜晶体硅太阳电池的反射率随波长的变化Fig.3 Variation of the reflectance of crystalline silicon solar cells with a double-layer MgF2(104nm)/ZnS(80nm) anti-reflective coating with wavelengths
根据文献[5]给出MgF2(104 nm)/ZnS(80 nm)双层减反射膜晶体硅太阳电池的膜系参量,通过光学干涉矩阵法计算出考虑色散下反射率随波长变化关系,图3中黑点符号和实线分别表示实验数据(文献[5]中图11所示数据)和考虑折射率色散效应的情况,发现考虑色散下反射率的理论计算值与实验数据符合较好,然后,计算出未考虑色散下反射率随波长分布关系,如图3中虚线所示.由此可见,考虑折射率色散效应情形时的数值计算结果与实验数据吻合较好,而未考虑折射率色散效应时的数值计算结果与实验结果相差较大,特别是在350~450 nm波长范围内.经过计算,得到考虑色散与未考虑色散效应下MgF2(104 nm)/ZnS(80 nm)双层减反射膜晶体硅太阳电池反射率的实验值和数值计算值的差方和s分别为4.94×10-3与1.40×10-2.由图3还可看出,减反射膜厚度相同情形下,在是否考虑折射率色散效应下所得的反射率数值计算结果有较大差别,在350~615 nm波长范围内,考虑折射率色散效应的反射率大于未考虑折射率色散效应情形,并且在350~500 nm波长范围内差别明显;在615~1 100 nm波长范围内,考虑和未考虑折射率色散效应情形下所得反射率差别极小.仍旧发现在350~370 nm波长范围内,考虑和不考虑折射率色散效应情形下的反射率随波长变化趋势完全相反,并且在图2中350~370 nm波长范围内反射率随波长变化趋势也是如此,由于在350~370 nm波长范围内基底硅的折射率随波长变化趋势同样是这种情况,原因是基底硅的折射率色散效应所造成的.说明一下,文献[5]中MgF2(104 nm)/ZnS(80 nm)双层减反射膜也采用电子束沉积,膜厚通过石英晶体监控,真空室压强为10-3∶10-4Pa,但ZnS与MgF2的沉积速率及衬底温度文献中均没有给出.
尽管上述所验证的减反射膜均为MgF2/ZnS双层减反射膜,都是采用电子束沉积,但所制备的各膜层厚度是不同的,实验条件也有差异,然而从上述考虑折射率色散效应下的数值计算结果和实验测量数据的对比来看,考虑色散效应下的数值计算结果均与实验测量数据更相符,尤其是在短波范围内,因此考虑折射率色散效应所得的反射率计算值与实际情况更接近,那么在膜系设计中考虑折射率色散效应是有必要的.
2 考虑折射率色散效应下的减反射膜设计
在晶体硅太阳电池减反射膜的设计中,所采用的算法为遗传模拟退火算法,由于遗传模拟退火算法的基本理论和具体实现过程在许多文献中都进行了详细的论述[12,14,17],这里就不再赘述.在减反射膜的设计中,考虑到AM0太阳光谱功率分布与硅的内部量子效率曲线不一致,将它们的乘积作为权重因子,得到在整个光谱范围内的加权平均反射率[5],即
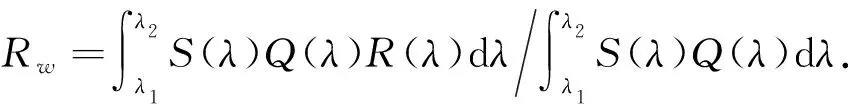
(3)
式中:S(λ)为AM0太阳光谱功率分布,这里用5 960 K黑体辐射光谱模拟AM0太阳光谱;Q(λ)为硅的内部量子效率;R(λ)为减反射膜在对应波长点的反射率;λ1和λ2为光谱波长下限与上限,λ1=350 nm,λ2=1 100 nm.在利用智能算法进行减反射膜设计中,将加权平均反射率作为评价函数,评价函数Rw的取值是以最小为最优.考虑色散与未考虑色散情形下减反射膜系设计中所使用遗传模拟退火算法的参数设置完全相同.
2.1 MgF2/ZnS双层减反射膜设计
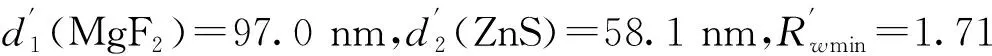
图4为考虑色散与否情形下通过智能优化算法参数反演所获得的MgF2/ZnS双层减反射膜的反射率,实线和虚线分别是考虑与未考虑色散下通过智能优化算法反演所得膜厚参量,均代入考虑色散下减反射膜反射率计算公式中得到的结果.从图4可知,在350~485 nm波长范围内考虑色散效应下的反射率小于未考虑色散的情形,在635~1 100 nm波长范围内考虑色散效应下的反射率大于未考虑色散的情形,分析原因是智能优化算法在膜厚参数反演过程中,由于基底硅和各层减反射膜材料的折射率在短波范围变化较大,而在长波范围变化较小,导致算法在膜厚参数优化中,主要考虑短波范围内的材料色散影响因素.
2.2 SiO2/ZnSe双层减反射膜设计
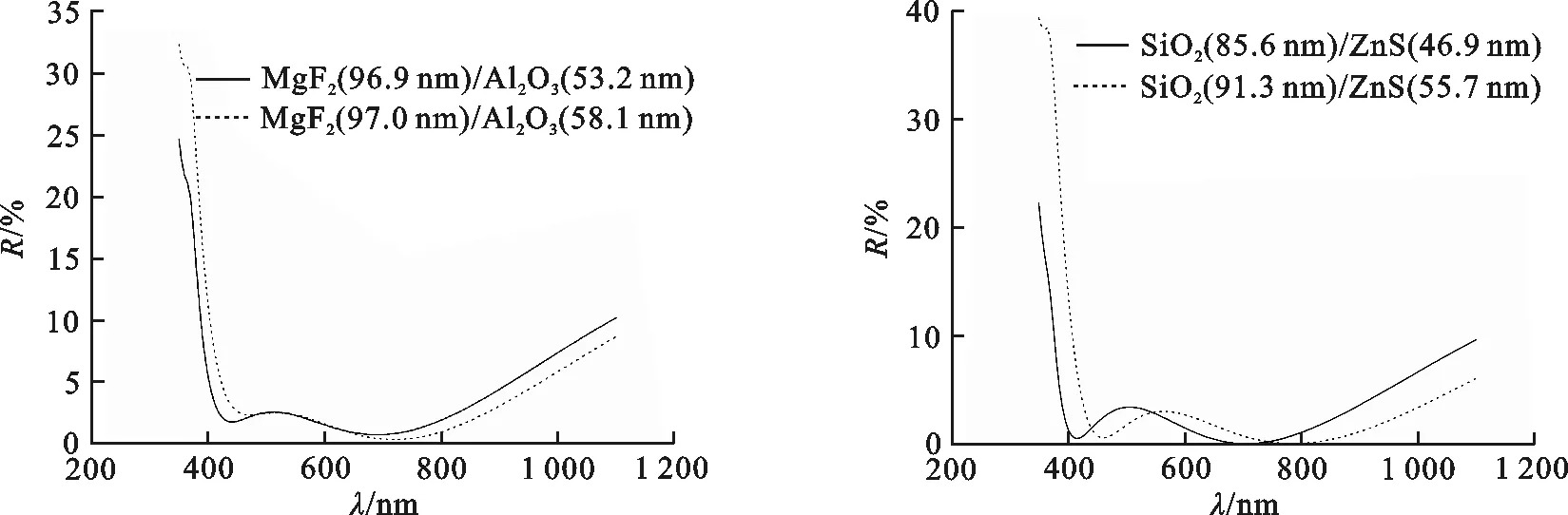
图 4 MgF2/ZnS双层减反射膜的反射率随 图 5 SiO2/ZnSe双层减反射膜的反射率 波长的变化曲线 随波长的变化曲线 Fig.4 Curves of the reflectivity of MgF2/ZnS double-layer Fig.5 Curves of the reflectivity of SiO2/ZnSe double-layer anti-reflective coatings with the wavelengths anti-reflective coatings with the wavelengths
图5为考虑与未考虑色散情形下通过智能优化算法参数反演所获得的SiO2/ZnSe双层减反射膜的反射率,实线和虚线分别是考虑与未考虑色散下通过智能优化算法反演所得膜厚参量,均代入考虑色散下减反射膜反射率计算公式中得到的结果.从图5可见,在350~440 nm波长范围内考虑色散效应下的反射率远小于未考虑色散的情形,在745~1 100 nm波长范围内考虑色散效应下的反射率大于未考虑色散的情形.出现上述现象的原因仍旧是智能算法在膜厚参数优化中,主要考虑波长较小范围内的硅基底和减反射膜材料的色散效应.
表1为考虑与未考虑色散下3种减反射膜的优化结果.从表1中考虑色散效应的优化结果来看,双层减反射膜材料的折射率相差越大,通过智能优化算法所得减反射膜的最小加权平均反射率越小,而且要满足与基底相邻的减反射膜的折射率大于外层膜的折射率时,才会有较好的减反射效果.

表 1 考虑与未考虑色散下两种减反射膜的优化结果
将表1中不考虑色散下所得几种材料的最佳膜厚参量,代入考虑色散效应下的加权平均反射率计算公式中,所得SiO2/ZnS、MgF2/Al2O3双层膜的加权平均反射率依次为Rwmin=3.88%,9.30%.与表1考虑色散效应下的结果比较发现,上述材料在不考虑色散效应下的加权平均反射率都相应大于考虑色散效应情形下的结果.经进一步计算,与不考虑折射率色散效应的膜厚优化结果代入考虑色散效应下的加权平均反射率计算公式所得加权平均反射率相比,考虑色散效应下SiO2/ZnS、MgF2/Al2O3减反射膜最小加权平均反射率,依次降低了7.73%,3.44%,说明双层膜的减反射效果在考虑色散效应下更佳.
图6,7分别为SiO2/ZnS和MgF2/Al2O3双层减反射膜的反射率,实线和虚线分别是考虑与未考虑色散下通过智能优化算法反演所得膜厚参量,均考虑色散效应下所得减反射膜的反射率,从图中发现,与不考虑色散相比,考虑色散下的反射率在短波区域内得到较大改善,但在长波区域内的反射率有所增加,但总体来讲,考虑色散情形下所设计的减反射膜更优.
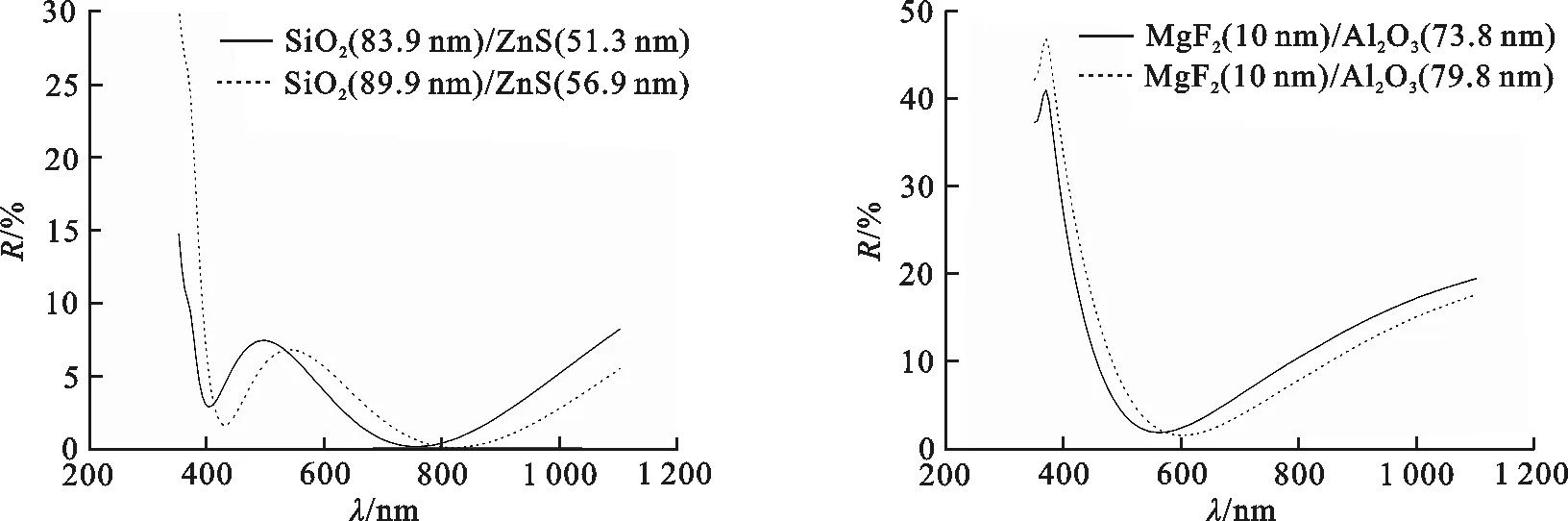
图 6 SiO2/ZnS双层减反射膜的反射率随 图 7 MgF2/Al2O3双层减反射膜的反射率随 波长的变化曲线 波长的变化曲线 Fig.6 Curves of the reflectivity of SiO2/ZnS double- Fig.7 Curves of the reflectivity of MgF2/Al2O3 double- layer anti-reflective coatings with the wavelengths layer anti-reflective coatings with the wavelengths
3 结束语
本文通过光学干涉矩阵法分别计算了考虑色散情形下MgF2(98 nm)/ZnS(70 nm)双层减反射膜和MgF2(104 nm)/ZnS(80 nm)双层减反射膜晶体硅太阳电池反射率的理论值,并与文献所提供的实验数据进行对比;在考虑折射率色散情形下,利用智能优化算法设计出硅太阳电池的双层减反射膜,并与不考虑色散情形下所设计的结果进行了比较.结果表明,与不考虑色散情形相比,考虑色散情形下反射率与实验测量结果更相符,特别是在短波范围内;考虑色散情形下通过智能优化算法所得减反射膜的加权平均反射率出现较大程度的减小.可见,折射率色散效应对于薄膜材料的光学性质具有重要影响,因此在进行晶体硅太阳电池的减反射膜设计中考虑色散效应是有必要的,后面将进一步研究色散效应对多层减反射膜,特别是对周期性结构减反射膜系设计的影响.
致谢:感谢上海电力学院太阳能研究所刘永生老师所提供的硅的内量子效率数据.

