基于时间Petri网的自动制造系统排产优化方法
王艺翔,洪 良,田海霖,王晓华
(西安工程大学 电子信息学院,陕西 西安 710048)
0 引 言
由于自动制造系统[1]中存在事件冲突性与并发性等特点,当前的算法和模型已无法满足自动制造系统的生产要求,因此,对排产的优化显得尤为重要.近年来对排产问题的研究,已经取得了许多成果.Johnson在20世纪五十年代提出解决车间调度部分特殊问题的优化算法[2],开启了对调度问题的研究;Roslof提出了一种基于整数线性规划的算法[3],但用该算法求解生产调度问题时,随着对象的增多和时间的推移会产生状态空间爆炸的问题;文献[4]将人工智能算法运用到排程问题之中,提高了生产效率,但不能保证收敛到最优解;文献[5-7]对遗传算法做了比较全面的总结,遗传算法可以对生产线上的个别工序进行优化,但局限于无法满足多任务生产的情况.Petri网[8-10]在处理离散事件系统问题不仅可以描述系统的静态行为,也可以描述系统的动态行为[11],简单准确地表示系统中的并发、资源共享、冲突、相互抑制以及非确定性等特征,图像界面直观清晰,这些特点都十分有利于自动制造系统的建模. 文献[12]应用Petri网理论解决了传统方法由于状态空间爆炸造成的寻优计算难题. 目前,Petri网理论已经在大规模车间生产调度问题[13-16]中得到广泛应用,文献[17-19]讨论了利用时间Petri网对系统的建模和分析,给出了自动制造系统生产过程的调度算法,但缺少对多条线路自动制造系统的分析和优化.
本文采用时间Petri网[20]建立系统模型,针对多线路自动制造系统,使用了减少缓冲器资源的策略,在添加控制器的基础上引入时间函数,解决冲突所带来的设备等待时间过长的问题,在节省缓冲器资源的同时,提高系统的生产效率.
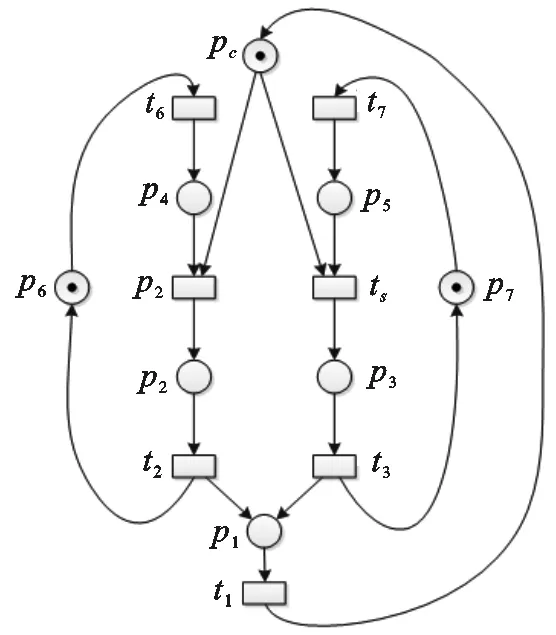
图 1 一个基本的时间Petri网单元Fig.1 A basic unit of time Petri net
1 时间Petri网
Petri网(PN)是一个五元组,可表示为N=(P,T,F,W,M0),其中:P代表库所的集合,库所P用圆表示;库所中包含的若干黑点,称为托肯(token);T代表变迁的集合,变迁t∈T用方框表示;F⊆ (P×T) ∪ (T×P),称为流关系或者有向弧的集合;W:(P×T) ∪ (T×P) →N,是一个映射,称为Petri网N的权函数,不进行特殊标注时,默认权函数为1;M0:P→N,是一个列向量,称为Petri网N的初始标识,表示初始状态下各库所中的托肯数. 一般用·p表示库所p的输入变迁集合,p·表示库所p的输出变迁集合,用·t表示变迁t的输入库所集合,t·表示的输出库所集合.PN的运行规则是:变迁t在标识M下是使能的,当且仅当∀p∈·t:m(p)≥i(p,t). 变迁t的激发将从·t中转移定量的托肯到t·中去,从而使Petri网的标识发生变化.
自动制造系统的工序通常和时间有关,在基本网中加入时间元素来表示时间信息,构成时间Petri网(TPN,timed petri nets).TPN分为3种,分别是给库所中的托肯赋以持续时间、给变迁赋以延时时间、给有向弧赋以时间权,本文采用第一种,库所时间Petri网(TPPN,timed place petri nets).TPPN是一个六元组,TPPN=(P,T,F,W,M0,D),其中P,T,F,W,M0的定义与基本网定义相同,D={d1,d2,d3,…,dn},表示库所中托肯的延迟时间.
2 问题描述
图1是一个简单的自动制造系统,该系统表示两条生产线同时开始工作,生产完成的部件由一个机械臂或小车来运输,用p1表示,两条生产线属于竞争关系,随时有可能产生冲突,造成系统死锁.在加入控制器pc后,两条生产线在缓冲器p1处的冲突问题得到解决,各库所的延迟时间如表1所示.
一般情况下,为平衡两条线路的生产任务,缓冲器对于生产线上已生产完成的工件是依次轮流接收,
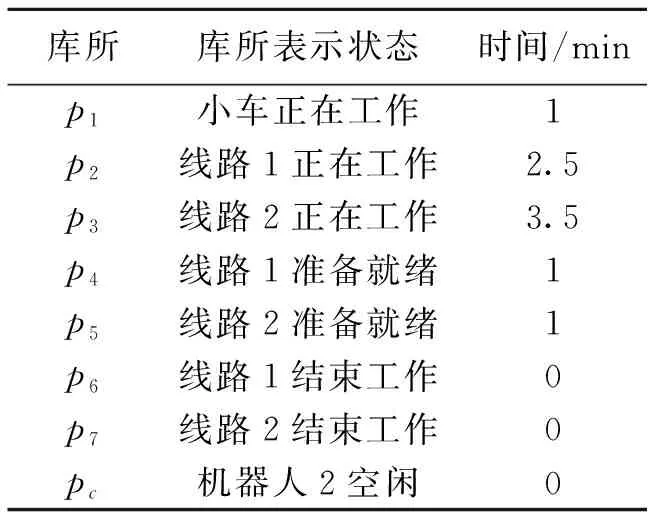
表 1 网模型中各库所在系统中的含义
因此造成大量的等待时间,造成浪费,如图2所示,其中,纵坐标“1”代表处于工作状态,“0”代表处于空闲状态.由图2可知,两条线路均有大量的时间处于空闲状态.但是,对缓冲器进行时间规划后,生产效率大幅提升.这种优化方式需要准确预测上一组任务的完成时间,在本例中,首先计算缓冲器何时为空.已知两条生产线路同时使用一个机器人作为缓冲器,通过计算时间,给生产线路和缓冲器赋予时间函数,在固定时刻开始某一工件的生产,缓冲器在特定的时刻与特定的生产线对接,如图3所示,生产率成倍增长甚至生产线2达到了100%.

图 2 生产线1和生产线2的一般工作状态 图 3 添加任务时间后的工作状态 Fig.2 The work duration of line 1 and line 2 Fig.3 Work duration of line 1 and line 2 by adding task completion time
在实际生产中,系统要比上例中的单元复杂.以3个机床和2个移动机器人的自动制造系统为例. 3个机床M1,M2,M3负责加工工件,R1,R2表示2个移动机器人把加工完成的工件运输到下一环节. 机床和移动机器人的工作时间如表2所示,由于机床生产单个工件时间长而机器人的运输时间较短,为了节省成本,不再使用移动机器人与机床分别对接的形式.需要解决以下问题:
(1) 避免冲突时间发生,在系统中添加控制器;
(2) 提高该系统的生产效率,减少资源浪费.

表 2 工件经过每个工序所需要的时间
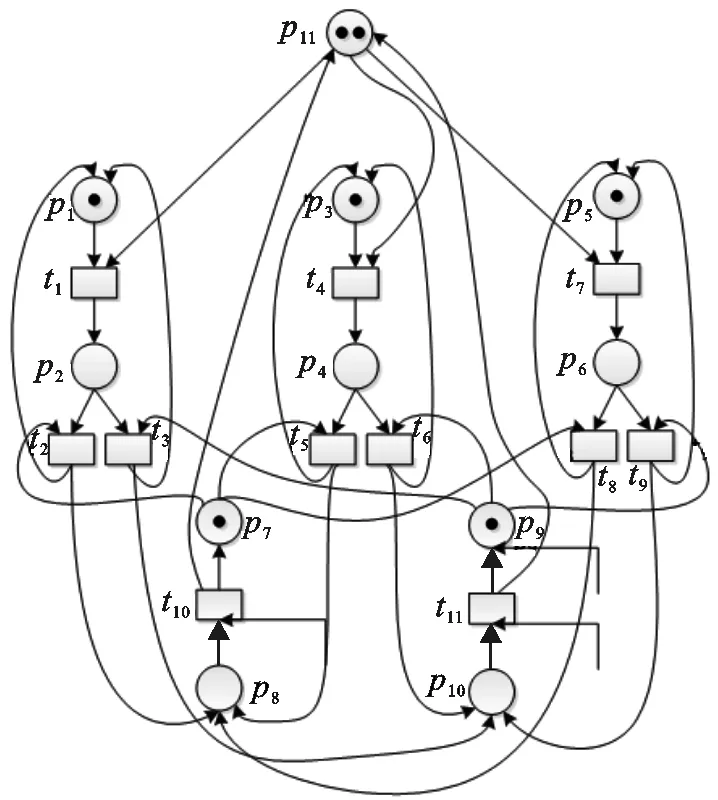
图 4 添加控制器后的Petri网模型Fig.4 The Petri net model of adding control place
添加控制器后的系统模型如图4所示,经过3个机床生产完成后的工件可以由机器人R1,R2中任意一个运输,以机床1为例,库所p2中的托肯通过t2,t3转移到p8或p10,同时在p1中产生新的托肯,代表机床1可以继续加工工件. 网模型的初始状态如图所示,M0=(1,0,1,0,1,0,1,0,1,0,2)T.p8或者p10中的托肯经过变迁t10或者t11同时在控制器中产生托肯,控制器中的最大托肯数为2,达到控制整个系统的目的. 通过控制器的协调,系统可以有序的进行工作,但通常情况下生产效率不够高,出现了资源浪费的情况. 因此,本文针对这种情况,给出了有效的算法.
3 算 法
在模型添加控制器后,生产过程中的某个工件进入机床开始生产通常是在上一个工件已经被机器人释放之后. 实际上,当机床将加工完成的工件送达机器人后,已经可以开始继续生产下一个工件. 利用这一思想,与两个机器人工作时间相对较短的特点相结合,达到提高生产率的目的. 主要步骤如下:
(1) 找到所有的基本回路,该回路从控制器开始并最终回到控制器;
(2) 省略控制器的输入弧,添加时间库所;
(3) 计算控制器中控制机床和移动机器人开始工作的具体时刻.
3.1 网模型基本回路判定算法
网模型中存在从某一节点出发最终回到该节点,并且所有节点只出现一次的回路,称回路上所有节点构成的向量为有向回路,用si表示,有向回路构成的集合Sc={si|i∈(0,j)}. 定义变迁集合Tc={tcm|tcm∈pc·,m∈(0,n)},pc表示控制器. 定义基本回路为所有包含tcm和pc的回路,用Se表示. 有向回路可能是多个基本回路的叠加,系统里面可能存在无数个有向回路,因此,需要从有向回路中提取出基本回路.基本回路表示能够完成一个工件生产所经过的最少元素的回路,经过计算和比较,最优回路在基本回路中产生. 已加入控制器的网模型中存在许多有向回路,从网模型中筛选出基本回路,可以判断每个回路中所用到的工序,再计算得到回路所有工序占用的时间,进行比较后确定最优回路.
算法1:判定模型中存在的所有基本回路;
输入:所有有向回路集合Sc;
输出:所有基本回路的集合Se;
step 0:定义一个集合Se:=∅,表示所有基本回路的集合;
step 1:for(i:=0;i≤j;i++)
for(m:=0;m≤n;m++)
ifsi中不包含tcm,Sc:=Sc{si};
step 2:while(Sc≠∅)
从Sc中选择一个si,Sc:=Sc{si};
ifsi中包含pc,Se:=Se∪{si};
step 3:输出集合Se;
step 4:结束.
通过算法1,可以找到网模型(如图4)中所有能够完成工件生产的基本回路集合Se,计算得到每个基本回路完成工作的时间,根据算法的整体思想,省略基本回路中控制器的输入弧,建立时间Petri网,如图5所示.继续根据时间Petri网中库所的延时时间D,通过算法2来计算得到最优时间,判断哪个回路是最优回路,确定控制器中的具体时刻. 最优回路即单位时间内设备资源利用率最高,产出的工件最多的回路,工件在最优回路上完成生产所消耗的时间称为最优时间.

图 5 应用本文算法建立时间Petri网模型Fig.5 The timed Petri net applying the algorithm
3.2 基本回路加工时间优化算法
算法2:确定第k+1个工件的最优回路所需时间,k+1表示第k个资源结束后的下一个资源;
输入:工件在加工进程上所需加工时间dn;工件在共享资源α中所需时间dα;工件在共享资源β中所需时间dβ;
输出:最优回路所需时间d0;
step 0:规定第一个工件使用第一个共享资源作为其最优回路;
step 1:定义一个变量d0为第k+1个工件在最优回路中所需时间;
step 2:switch(dα与dβ的比较,是否有共享资源闲置)
case(dα case(dα=dβ,且此时共享资源α,β均闲置)则该工件占用共享资源α,d0:=dn+dα; case(dα>dβ,且此时共享资源β闲置)则该工件占用共享资源β,d0:=dn+dβ; case(此时无共享资源闲置)则开始等待, step 3:输出d0; step 4:结束. 通过设计算法2,计算找出每个工序的最优回路和最优时间,通过控制器按照最优排列顺序工作,可以避免由系统的异步性产生的冲突,得到更加高效的排产结果. 依据表2中所给出的各项工序所需要的时间,由算法1可以找到图4模型中存在的所有基本回路,省略控制器的输入弧,即[t10,p11],[t11,p11],建立TPN.应用算法2,对比各条基本回路所用时间,计算出最优排列顺序,从而得到系统生产的最短时间. 图6是加上传统控制器时系统的排程结果,可以看出,虽然系统稳定工作,但是排程上出现了大量空闲时间,造成了资源浪费.运用本文算法计算结果如图7所示,在同一条件下,整个系统的工作效率明显提升,机床2的排程已经达到了100%.在实际操作中,需要提前计算各环节的准确时间,在系统开始工作之前,将时间函数输入到控制器之中,要求系统按照计划时间工作,才能达到本文中的效果. 图 6 未优化前的排产结果Fig.6 Production schedule before being optimized 图 7 应用本文算法的排产结果Fig.7 Production schedule applying the algorithm 在当前对自动制造系统排产的研究中,应用添加控制器的方法避免了系统发生冲突和死锁问题,但是生产效率没有明显提升.本文在自动制造系统中建立时间Petri网模型,通过适当的计算,在控制器中加入时间函数,得到优化后的时间排程,在实际生产中具有可操作性.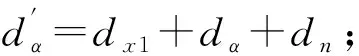

4 计算结果


5 结束语

