山西省人均GDP的发展态势

蔡建哲

（吉林大学，吉林 长春 130012）

人均GDP是发展经济学中衡量经济发展状况的指标，是人们了解和把握一个国家或地区的宏观经济运行状况的有效工具，它的增长具有一定的内在规律性，深入分析这一指标对于反映我国经济发展历程、探讨增长规律、研究波动状况，制定相应的宏观调控政策有着十分重要的意义。具体到山西省而言，十九大之后的发展期是确保全省完成2020年全面建成小康社会的关键时期，是确保全省转型综改试验区建设取得重大进展的攻坚时期，同时也是确保全省转变经济发展方式取得实质性进展的战略机遇期。它事关全省经济社会发展全局，具有特殊重要的地位，制定好省十九大之后发展期规划意义重大而深远。本文针对十九大之后发展期我省经济和社会发展的主要指标进行预计测算，为我省十九大之后发展期规划提供数据支持。依照理论基础，从《中国统计年鉴》及《山西统计年鉴》整理出山西省1978年到2017年人均GDP的数据，将其作为样本确立数学模型并预测山西省人均GDP的发展趋势。

一、ARMA模型建模过程

1.1 平滑处理

ARIMA模型构建首先要保证时间序列数据的稳定性，以通过时间序列的散点图或折线图进行检验。如果出现不稳定的数据时，对数据取对数或进行差分处理。

图1.1.1 Y（人均GDP）、DY（一阶差分）和DY2（二阶差分）的趋势图

图1.1.1分别为Y（人均GDP）、DY（一阶差分）和DY2（二阶差分）的趋势图，由这些图可以看出，Y（人均GDP）呈现明显的指数增长趋势，DY（一阶差分）呈现出明显的增长趋势，DY2（二阶差分）可能平稳，所以尝试去DY2进行建模处理。

利用包含截距项但不含有趋势项的检验回归模型对序列DY2进行ADF检验，结果表明，ADF检验统计量t统计量为-6.150798，分别小于5%和10%的检验水平下的临界值-3.621023和-2.943427，且P值为0.0000，小于0.05，通过检验，所以DY2是平稳的。

1.2 模型识别

用自相关系数和偏自相关系数，确定ARIMA模型的阶数和模型的系数。

表1.2.1为DY2的自相关与偏相关图，可以看出样本的自相关图和偏自相关图都是拖尾的，我们初步选用ARMA(1,1)模型。

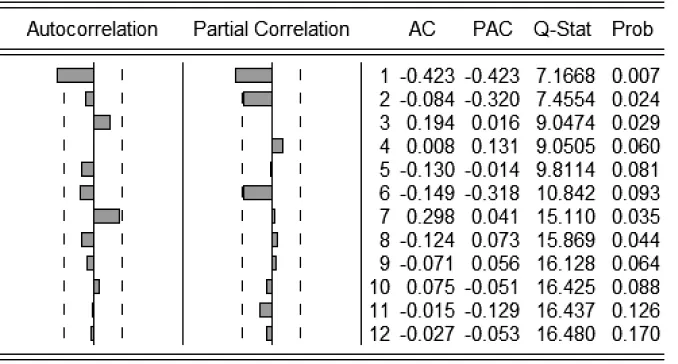
表1.2.1 DY2的自相关与偏相关图

1.3 模型估计

在确定数据模型的阶数以后，就该对ARIMA模型的设计参数进行估计。

表1.3.1为ARMA模型参数估计结果，可以认为所估计的ARMA(1,1)模型是平稳的且是可逆的，模型拟合情况比较好。

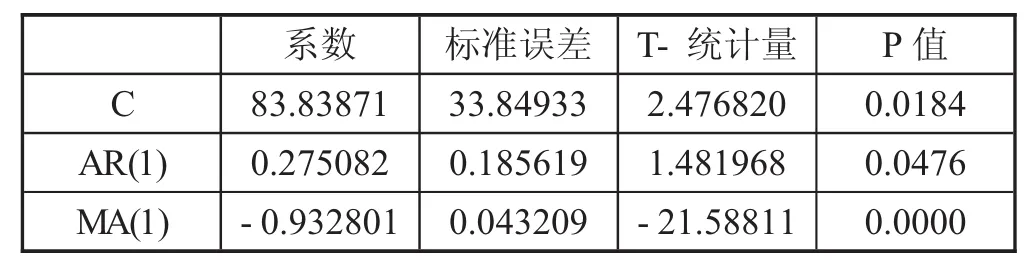
表1.3.1 ARMA模型参数估计结果

1.4 模型预测

图1.4.1为ARMA(1,1)模型预测结果，从预测结果来看，Theil不相等系数为0.54，其中协方差比例约为0.70，表明模型的预测结果较理想。

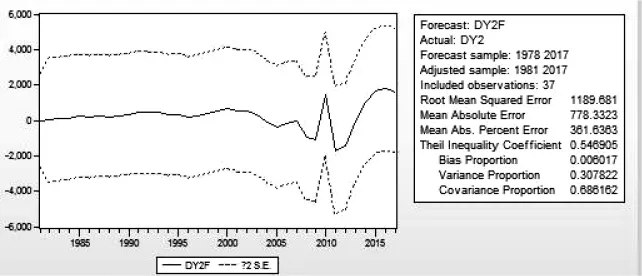
表1.4.1 模型预测结果

二、最小二乘回归建模过程

2.1 参数估计

利用LNY（人均GDP对数处理结果）、T（时间）和DLNY（LNY的一阶差分）做最小二乘回归，得到的参数如表2.1所示，可以看出，全部都通过检验。由于自然函数具有递增单调性，所以上一年的人均GDP对本年人均GDP存在正影响，这也是符合实际情况的。因此，模型拟合较好。

表2.1 最小二乘回归参数估计结果

2.2 模型预测

Eg：预测2015年数据

根据2.1中得出的最小二乘模型，LNY=-256.0818+0.132347T+0.743696DLNY，将2015年数据输入，可得2015年人均GDP取对数后的预测值为10.5962，实际数据为10.4658，则预测误差为0.1282，可见预测效果也是很好的。

三、分位数回归建模过程

3.1 参数估计

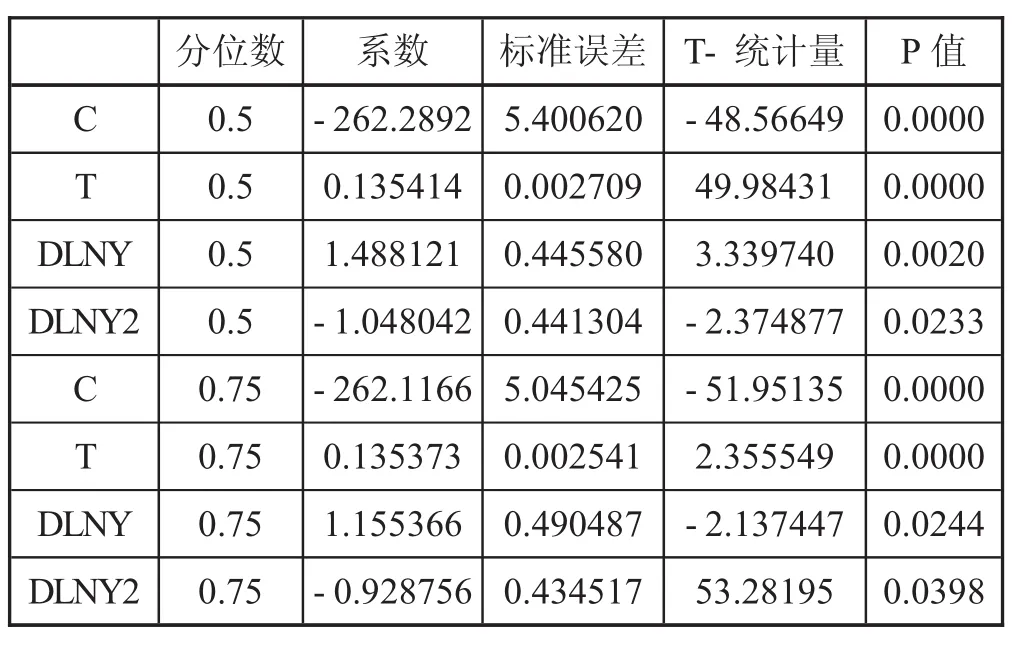
表3.1 分位数回归的参数估计结果

利用LNY（人均GDP对数处理结果）、T（时间）、DLNY（LNY的一阶差分）和DLNY2（LNY的二阶差分）做分数分别为0.5和0.75的分位数回归，表3.1为分位数回归的参数估计结果。

从表3.1可以看出，所有P值均小于0.5，回归效果还是很好的。

3.2 模型预测

图3.2为不同分位数下，分位数回归模型预测结果，从预测结果来看，Theil不相等系数分别为0.01和0.01，其中协方差比例分别约为0.70和0.90，可以表明模型的预测结果比较理想。

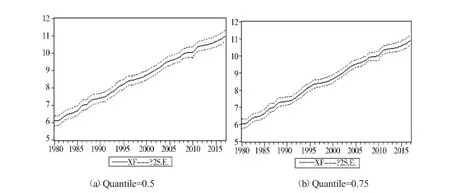
图3.2 分位数回归预测结果

四、各模型进行预测比较

统一选取2015年作为对比年份，利用三个模型对2015年的数据进行预测和检验，比较结果如表4.1所示。

从表4.1可以看出，最小二乘法回归模型的预测结果最好，ARMA(1,1)模型预测结果对比其他模型，效果不是很理想。

从三模型预测的结果来看，山西在今后的几年能有望保持一个较高的增长态势。而山西省又是目前国家批准的唯一一家在全省域、全方位、系统性地进行资源型经济转型综合配套改革试验的区域，这给山西的发展带来一个前所未有的机遇，山西省人均GDP将会有很大的增长空间。