面向编队飞行的天文多普勒差分/脉冲星组合导航

喻子原，刘劲，宁晓琳，马辛，桂明臻，康志伟

（1. 武汉科技大学 信息科学与工程学院，武汉 430081；2. 北京航空航天大学 仪器科学与光电工程学院，北京 100191；3. 湖南大学 信息科学与工程学院，长沙 410082）

0 引 言

传统的航天器导航方法，如天文导航系统[1]、地磁导航系统[2]等都是与地面站进行信息交流，仅能在地球附近提供高精度的导航信息。在深空探测中，航天器离地面距离遥远，这会导致信号的严重滞后，无法为航天器提供精确的、实时的导航信息。因此，许多国家都在进行航天器自主天文导航系统[3-4]的研究，完全不依赖地面支持的自主导航系统是当今研究的热点。

太阳的方向矢量常作为量测量，但航天器与太阳距离较远时会导致测量误差极大。许多学者提出利用太阳多普勒频移来测量航天器相对于太阳的速度，但基于太阳频移的导航系统是不完全可观测的，不能单独工作。崔平远等提出将脉冲星和多普勒频移相结合的导航方法[5-6]，但太阳表面的活动会导致太阳光谱线的漂移，难以直接利用太阳频移测得航天器的绝对速度。刘劲等提出了面向编队飞行的太阳频移径向速度差分的测量方法[7]，该方法消除了太阳表面活动引起的测量速度误差，但太阳系中只有一个太阳，难以提供多方位的速度信息。

恒星多普勒差分导航[8]的原理和太阳多普勒差分导航相似，均利用光谱频移获得多普勒速度信息。面向编队飞行的恒星多普勒差分导航可以很好地解决部分恒星的径向速度难以确定的问题。与太阳多普勒差分导航相比，恒星多普勒差分导航具有其局限性：星光较弱，测量精度低，单独使用测量时误差较大[9]，但其优点是可提供多方位的速度信息。

脉冲星是高速旋转的中子星，它对外不断辐射唯一的、极其稳定的、具有可预见性的脉冲信号[10-11]。当采用3个及以上脉冲星时，系统便完全可观测[12]。X射线脉冲星导航[13-16]利用脉冲到达探测器的时间与到达太阳系质心的时间作为量测量，进而求得航天器相对于太阳系质心的位置矢量。但该导航系统的滤波周期较长，难以得到连续的导航信息。

综上所述，太阳光谱频移测速精度高，难以提供多方位速度信息；恒星光谱频移测速可提供多方位速度信息，但精度低；两种测速方法的组合导航系统不完全可观测；但利用3颗及以上的脉冲星导航是完全可观测的。

鉴于以上3种方法具有互补性，可组合利用。该组合导航中的量测量有3个：太阳径向速度差分、恒星径向速度差分和脉冲到达时间。鉴于轨道动力学模型和测量模型的非线性，针对深空探测火星环绕段选用扩展卡尔曼滤波器（Extended Kalman Filter，EKF）作为导航滤波器进行信息的融合[12]，并分析了不同太阳频移精度、不同天文多普勒差分测量周期对该组合导航方法精度的影响。该组合导航方法具有可靠性高、易于实现的特点，可以为火星探测提供一种方案参考。

1 导航方法

1.1 天文多普勒差分导航

在传统导航方法中，大多是利用天体的方位作为量测量。航天器上的光传感器可以精确测量天体的方向，但测量精度随航天器与天体的距离增大而下降。实际上，天体的方向和光谱都可以作为导航信息。航天器相对于光源运动，光谱线会从原来的位置发生移动，可以根据该移动量来获得航天器相对于天体的速度。

考虑到太阳表面活动对太阳光谱线的影响，可利用面向编队飞行的航天器径向速度差分来消除该影响。太阳径向速度差分测量的是太阳频移，测量对象是径向速度差分，它不受太阳表面活动引起的变化误差影响。其原理如图1所示，该径向速度差分表示为[7]

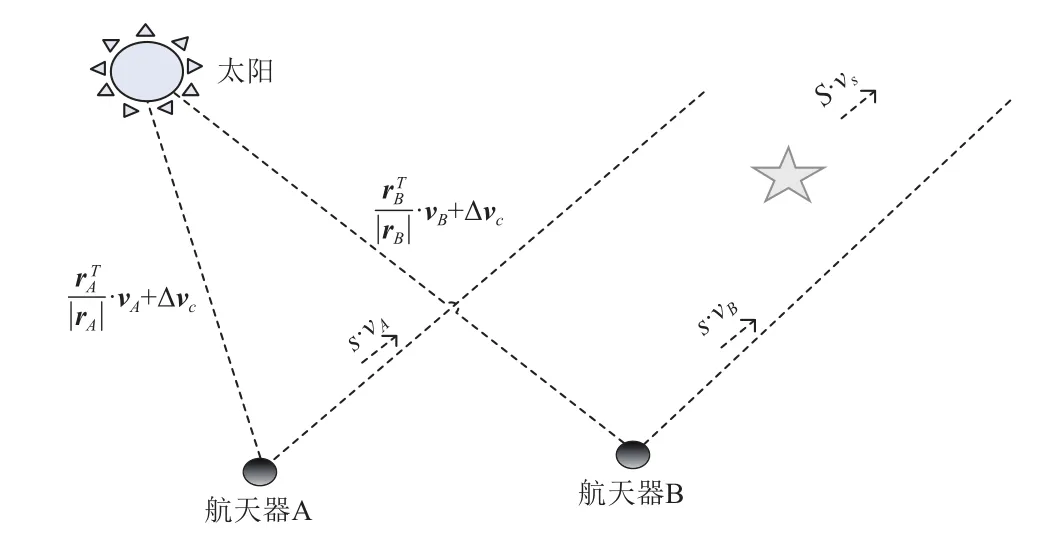
图1 天文多普勒差分导航Fig. 1 Celestial Doppler difference navigation

在测量过程中，考虑到航天器上分光计造成的测量干扰，假设为和，则径向速度差分可以表示为

基于太阳径向速度差分测量模型可以描述为

同太阳多普勒频移相似，利用恒星星光多普勒频移可以得到航天器相对于恒星的速度。基于IFIM（Instream Flow Increcement Method）的导航恒星选取策略，计算在不同导航恒星下的Fisher信息逆矩阵的迹，以拥有最小迹的星为导航星[8]。考虑到恒星径向速度难以确定，利用面向编队飞行的多普勒差分作为量测量消除恒星径向速度的影响。和分别为航天器A、B的速度矢量，是恒星的方向矢量，是恒星速度，分光计的测量误差为和，则两个航天器在导航星视线方向上的相对速度可表示为

基于恒星的径向速度差分测量模型为

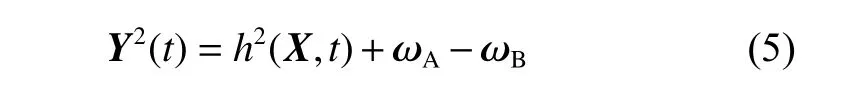
从式（5）中可以得到，恒星径向速度多普勒速度差分与恒星的径向速度测量无关，该方法能很好地应用于编队飞行。

1.2 X射线脉冲星导航

X射线脉冲星导航是以脉冲到达探测器的时间和到达太阳系质心（Solar System Barycenter，SSB）的时间作为量测量，其中脉冲到达探测器的时间t由X射线探测器观测得到，脉冲到达SSB的时间利用脉冲星计时模型预测得到[12]。脉冲星导航的基本原理如图2所示。

图2 脉冲星导航Fig. 2 Pulsar navigation

考虑相对论的影响，量测模型可以表示为

其中：c为光速；是脉冲星到达太阳系质心的距离；为 太阳系质心相对于太阳的位置矢量；表示太阳引力常数。

2 导航信息融合

在深空探测自主导航系统中，状态模型和测量模型参考文献[8]。鉴于状态模型和测量模型的非线性，采用具有良好非线性预测能力的EKF作为导航滤波器。滤波时，测量数据包括太阳/恒星多普勒差分和脉冲到达的时间。滤波过程包括预测和更新。预测是由轨道动力学模型来实现，更新是由测量的数据来实现。

由于X射线脉冲星导航的滤波周期较长，可以根据脉冲到达与否分两种情况来设计测量模型。

1）脉冲星观测期内，量测量为太阳/恒星多普勒差分。

相应的测量方程为

2）获得脉冲到达时间，量测量为脉冲到达时间、太阳/恒星多普勒差分。相应的测量方程为

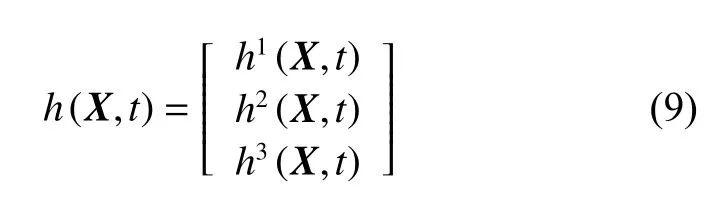
天文多普勒差分/脉冲星组合导航系统如图3所示。

图3 天文多普勒差分/脉冲星组合导航系统Fig. 3 Celestial Doppler difference/pulsar integrated navigation system

3 实验仿真

3.1 仿真条件

以火星环绕段为例，编队飞行的航天器A、B的轨道信息如表1所示。仿真时间是从1 Jul 2007 12 : 00：00.00UT到2 Jul 2007 12 : 00 : 00.00UT。导航滤波器参数如表2所示。X射线脉冲星方位参数如表3所示。考虑恒星星等对多普勒测量精度影响较大，故选择星等较低的天狼星为导航恒星，其方位如表3所示。

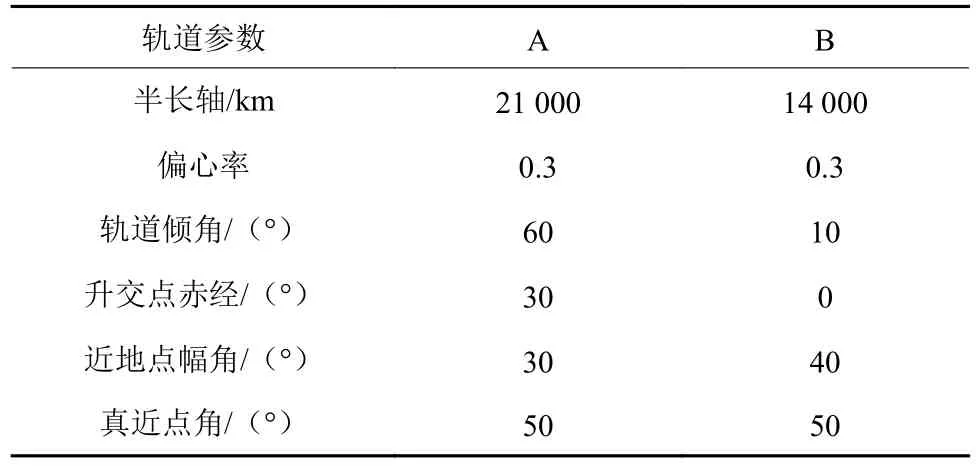
表1 航天器轨道参数Table 1 Spacecraft orbital parameters

表2 导航滤波器参数Table 2 Navigation filter parameters

3.2 仿真结果

图4是3种导航方法的估计误差。从图4中可以看出3种导航方法均能很好地收敛，都能获得高精度的导航信息。

图4 3种导航方法的估计误差Fig. 4 Estimation error of three navigation methods

经过100次的蒙特卡罗模拟实验，从图4和表4可以看出，与太阳多普勒差分/脉冲星组合导航以及恒星多普勒差分/脉冲星组合导航相比，在绝对位置上，天文多普勒差分/脉冲星组合导航分别提升了9.89%和31.48%；在绝对速度上，天文多普勒差分/脉冲星组合导航分别提升了10.96%和2.28%；在相对位置上，天文多普勒差分/脉冲星组合导航分别提升了16.59%和29.66%；在相对速度上，天文多普勒差分/脉冲星组合导航分别提升了27.69%和12.73%。

从表4中可以知道，天文多普勒差分/脉冲星组合导航在相对导航精度上有较大提高，这是因为多普勒差分导航是一种相对导航方法。

表4 3种导航方法的比较Table 4 Comparison for three navigation methods

接着，分析了太阳频移测量精度对天文多普勒差分/脉冲星组合导航的影响。图5给出了不同测量精度下的仿真结果。从图5中可以看出，随着太阳多普勒测速精度的提高，绝对和相对导航精度也相应地提高。当太阳频移测量精度达到1 m/s时，继续提高测量精度对组合导航精度的提升不大，这说明该组合导航方法对仪器的精度要求不高。

除此之外，本文还分析了当脉冲信号观测周期不变，天文多普勒差分测量周期变化时，天文多普勒差分/脉冲星组合导航的精度变化情况，其仿真结果如图6所示。

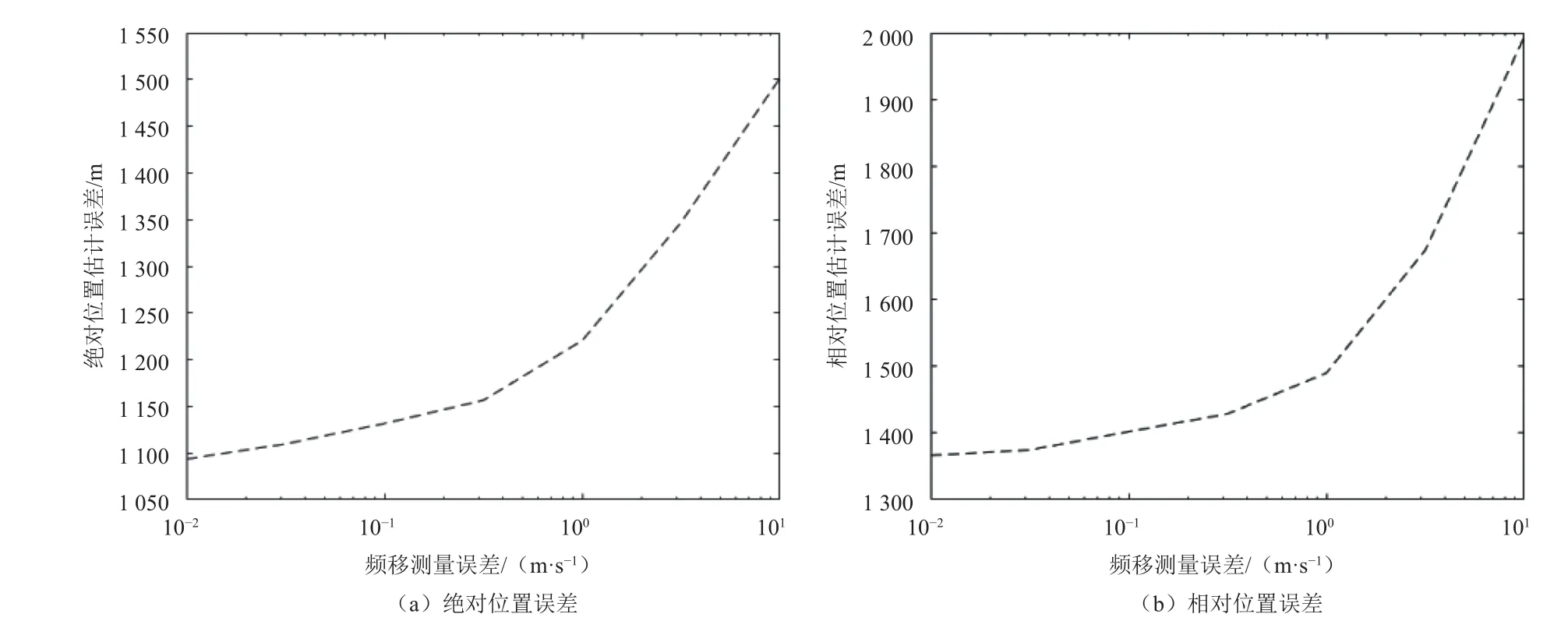
图5 不同太阳频移测量误差下的精度比较Fig. 5 Accuracy comparison for different Solar frequency measurement errors

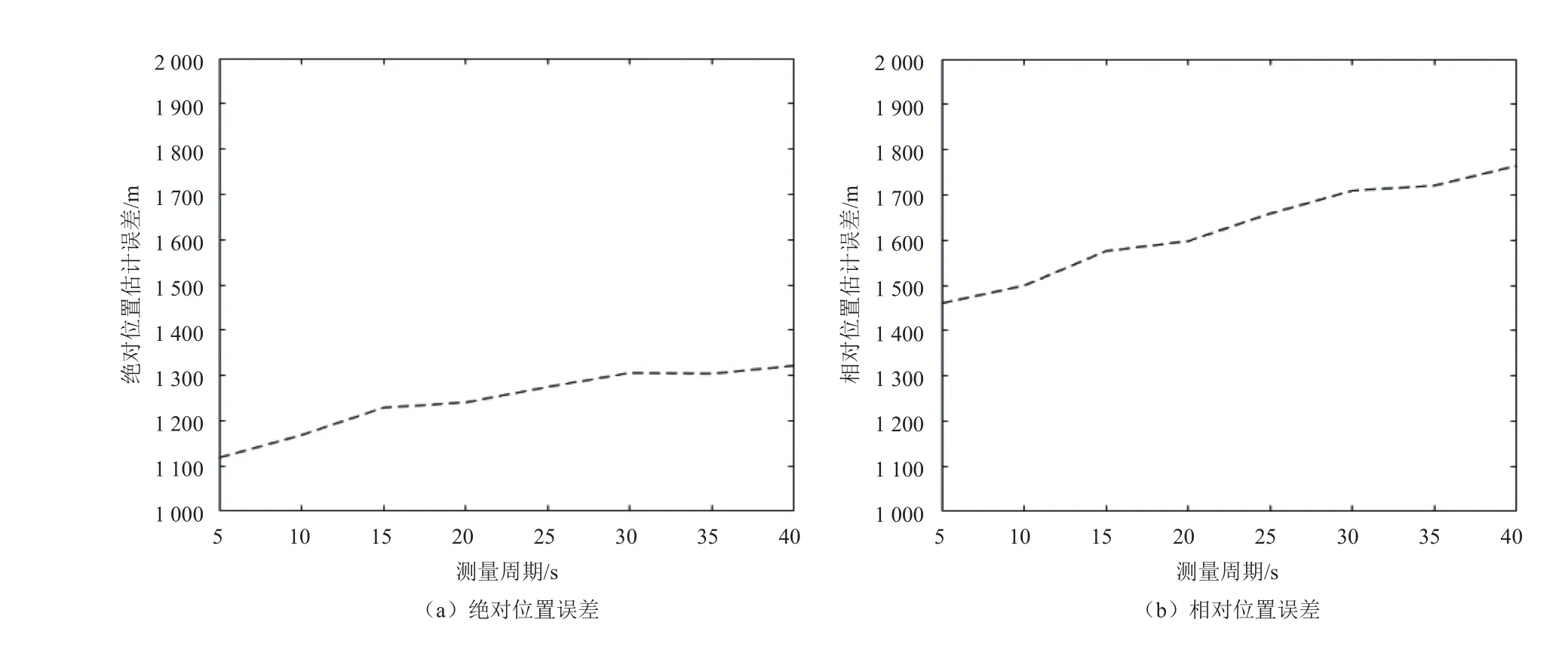
图6 不同天文多普勒差分测量周期下的精度比较Fig. 6 Accuracy comparison for different celestial Doppler difference measurement periods

从图6可以看出，当脉冲信号观测周期不变，天文多普勒差分/脉冲星组合导航的精度随天文多普勒差分测量周期的增大而降低。这是由于天文多普勒差分测量周期的增大导致测量数据的减少，进而影响了组合导航的精度。

4 结 论

本文针对深空探测的火星环绕段，提出了面向编队飞行的天文多普勒差分/脉冲星组合导航方法。该方法结合了太阳多普勒差分、恒星多普勒差分、脉冲星导航方法的优点，以EKF为导航滤波器，实现了3种导航方法的信息融合。除此之外，分析了太阳频移测量精度、不同的测量周期对该组合导航的影响。仿真结果表明该组合导航方法对仪器的精度要求不高，能够为编队飞行的航天器提供高精度的导航信息。因此，该组合导航方法具有可靠性高、易于实现的特点，能满足火星环绕段的导航任务。