基于群决策-熵模型的评标专家可靠性评价*

徐雯

(华中农业大学公共管理学院，湖北 武汉 430070)

0 引言

随着我国《评标委员会和评标办法暂行规定》《评标专家和评标专家库管理暂行办法》等相关法规的出台，评标专家在招投标中所起的作用越来越突出[1]，其行为直接影响招投标程序的规范性、过程的公平性和结果的公正性。然而在工作实践中，由于对项目熟悉程度、评标环境、专业知识结构、价值观念、道德品行、个人偏好等主客观因素的共同影响，使得部分专家往往给出非理性甚至是不合理的评价，在一定程度上造成评标结果有失客观性、科学性。因此，有必要界定异常性评分的标准，对评标专家的可靠性进行分析，并以此作为其入选或退出评标专家库的依据，从而有效监管评标专家的裁量权，保障评标结果的科学性。

目前，学界和业界对评标专家的可靠性进行了多方有效探索，包括：运用PageRank迭代算法对评审专家信誉度进行量化[2]；基于模糊算法和层次分析法构建评标专家考评机制[3]；从系统偏差、非共识偏差、同行偏差和偶然偏差4个方面构建评标专家异常性评分的判定方法[4]；探讨多属性评价活动中评审专家可信度的评价准则，并建立专家的评价水平排序和分类方法[5]等。这些研究，为评标专家可靠性的量化分析提供了重要的参考思路和方法借鉴。由此，本文拟构建群决策-熵模型，以期为评标专家可靠性评价提供一种简洁的量化方法。

1 理论基础与模型构建

1.1 群决策定义及过程[6]

决策所面对的问题通常是多目标、多方案、多学科领域的，且具有一定的不确定性，须由多个决策者组成具备不同知识结构、可以相互启迪的决策群体，以保证决策的科学性。这种由多人参加，以群体为主体所进行的决策活动被称为群决策。1987年，Hwang等给出了一个群决策的定义，即“将不同成员的关于方案集合中方案的偏好按某种规则集结为决策群体的一致或妥协的群体偏好序”。目前，学者们将群决策理论与其他学科相结合，展开了丰富的跨学科交叉研究。由于不同学科对群决策概念的界定有所不同，因而目前尚未形成被广泛接受的统一定义。

基于方案评审过程的特点，本文不失一般性地将群决策定义为“由一定组织形式的群决策成员，面对共同的环境，为解决存在的问题并要达到预定的目标，依赖一定的决策方法和方案集，按照预先制定的协同模式进行的决策活动”。因而，方案评审中的群决策过程可被描述为：每个专家对不同方案进行独立评审，即专家根据评标文件要求给出自己对方案的判断或偏好；按照预先确定的计分规则及每个专家的评审结果计算方案得分，即对所有专家的决策结果进行集结；根据方案最后得分进行优劣排序，即依据群决策结果确定最优方案。当群决策结果不满足一致性要求时，还需调整决策者偏好，直到达成群体一致的决策为止[7]。

1.2 熵理论及应用思路

熵，表征体系的混乱程度。这一概念最初来源于热力学，之后被Shannon用于定义信息(或实验)的不确定(或可靠)性，从而奠定了现代信息论的基础。邱菀华等通过对工程项目组织与管理问题的分析，提出基于熵的工程管理决策方法，进一步丰富了管理决策理论[8]。正如前文所述，工程项目评标是一个群决策过程，评标结果受到专家个体决策水平的影响，而评标专家个体难以做出完美决策，甚至可能会犯错误。因而，可利用成员个体评价结论的不确定性，即专家个体的决策熵，来评价专家的可靠性。

设S1,S2,…,Sm为m个专家，他们组成决策群G。待评对象或方案共有n个，分别记为B1,B2,…,Bn。xij为专家Si针对方案j给出的独立评审分值(i=1,2,…,m;j=1,2,…,n)。xij越大，表明Si对方案Bj的评价越高，越认同。专家Si对所有方案的评价结果构成向量xi=(xi1,xi2,…,xin)T，决策群G对所有方案的评价结果构成矩阵x=(xij)m×n。假设S*为理论评标专家，即该专家的评分相较于现实中任何一个专家的评分都更为准确和公正，其决策水平是最高的，决策行为是最可靠的。将专家S*的评分结果记为x*=(x*1,x*2,…,x*n)T∈En，根据评分可确定待评价方案的名次向量为N*=(N*1,N*2,…,N*n)。可以推断，评标专家Si的决策水平越低，所给结论与S*相差越大。这一“差异”即评标专家的决策熵，反映了评标专家Si的决策水平，可用来衡量其可靠性。

1.3 群决策-熵模型

1.3.1 评分值单位化

将专家给出的评分值进行单位化处理，见下式

Di=(di1,di2,…,din)T∈En

(1)

D=(D1,D2,…,Dm)T=(dij)m×n

(2)

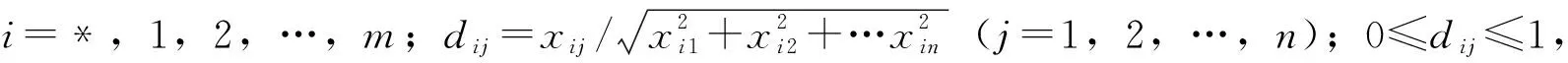
1.3.2 个体决策水平向量

以Ni=(Ni1,Ni2,…,Nin)表示按专家Si(i=*,1,2,…,m)的评分大小排列的方案优劣名次，则

Ei=(ei1,ei2,…,ein)

(3)

eij=1-N*j-Nij-d*j-dij

(4)

式中，i=*,1,2,…,m；j=1,2,…,n。

由此推断，理想专家S*的决策水平向量为E*=(1,1,…,1)，向量中各分量均为1，即达到最大值，说明其决策水平最高。专家Si的决策水平向量为Ei，向量中各分量值越小，说明其决策判断与理想专家所给结果的差异越大，即该位专家决策的可靠性越低。

1.3.3 个体决策熵

通过计算，可得到专家Si决策水平向量的分量广义熵之和Hi，以此作为专家Si的个体决策熵，用以描述专家Si决策结论的不准确性，衡量其决策水平。具体算法如下

(5)

(6)

式中，i=*,1,2,…,m；j=1,2,…,n。

专家Si的决策结论不准确性越小，其决策结论越可靠，则个体决策熵值越小。这一结论与现实情况相符，即高水平评标专家的决策失误很少，决策结论的可靠性高，决策熵值Hi很小。

1.3.4 群组决策熵

群组G的整体决策水平测度函数为

(7)

式中，Hi为群组G中各专家的个体决策熵；HG为群组决策熵，简称群组熵。群组熵小，则该群组的决策水平高，所给出的评审结论可靠。为提高群组决策水平，对于个体决策熵较小的专家应予以保留，并提高其个体集结权重；对于个体决策熵较大的专家，应降低其个体集结权重，甚至考虑用其他专家代替。

2 案例分析

2.1 评价原理

测度事物的优劣等级通常可经由两步完成：第一步，确定刻画优劣等级的标准或指标；第二步，用拟定的标准或指标去测度目标事物。一方面，被评价对象的优劣等级在客观上存在着某种概率分布；另一方面，任何量具都存在随机因素的干扰，即量具本身存在误差。也就是说，获得的测量值不可避免会出现波动，这一波动既是由于客观真实值自身有波动，也是源于所用量具带入了误差。在建设项目评标过程中，不同的参评方案完全可被视为某种工程产品或零部件。依照特定的评审标准及评价方法，参评方案的优劣等级是一个某种概率分布下的客观真实值。参评方案获得的优劣等级评分，则是对参评方案优劣进行测度后获得的测量值。量具是将真实值显现为测量值的工具，即通过量具来实现测量值的分布，而在建设项目评标过程中，评标专家便是一类特殊的量具[9]。

参评专家给出的评价结果存在一定差异，原因是每个专家的评价结果除了受到客观真值分布的约束外，还会受到客观不确定随机因素和主观系统因素的影响。所有影响因素与客观真值分布共同导致了具有偶然性的评价结果出现。若X为参评方案评价指标的真实值，Y为评标专家对X的评价结果，即测量值。X的分布为理想化的客观真值分布，且独立于任何评价专家；Y的分布则依赖评价指标的客观真值分布和特定的评标专家。所以，Y的波动σy不仅受到X波动σx的影响，还受到随机因素和主观系统因素所导致的误差波动σε的影响，即考核专家决策水平的依据，便是该专家在评标活动中给出的评价结果值Y。该值越接近客观真实值，则表明该专家的决策水平越高。如前所述，Y值的波动来自两方面，由于σx无法控制，因此无须考虑，而专家自身带来的波动σε是可以通过选择高水平专家来控制的。前文所介绍的通过群决策-熵模型所计算得到的各个专家的个体决策熵，在一定程度上反映了专家自身波动程度σε的大小，是对专家可靠性的具体量化。

σy=σx+σε

(8)

2.2 算例演示

工程项目A，采取公开招投标方式选择施工单位。参加投标的承包商中共有3家通过资格预审，分别记为B1,B2,B3。从专家库中选取5名专家作为评标委员，并以第一阶段技术标施工方案为算例进行演示[10]，具体评分结果见表1。

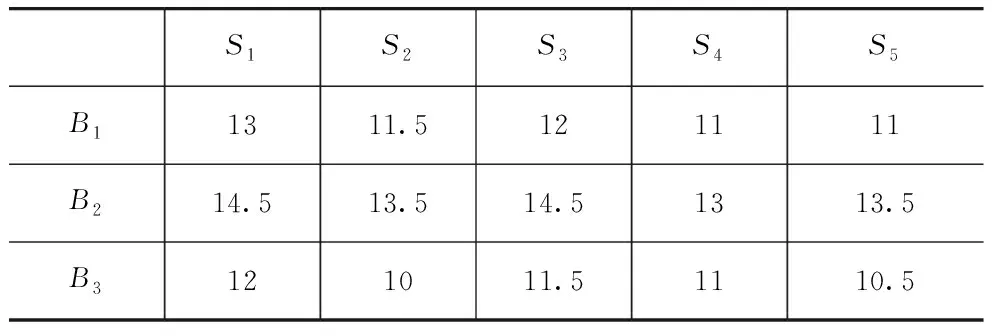
表1 技术标段施工方案专家评分结果

2.2.1 理想专家评分

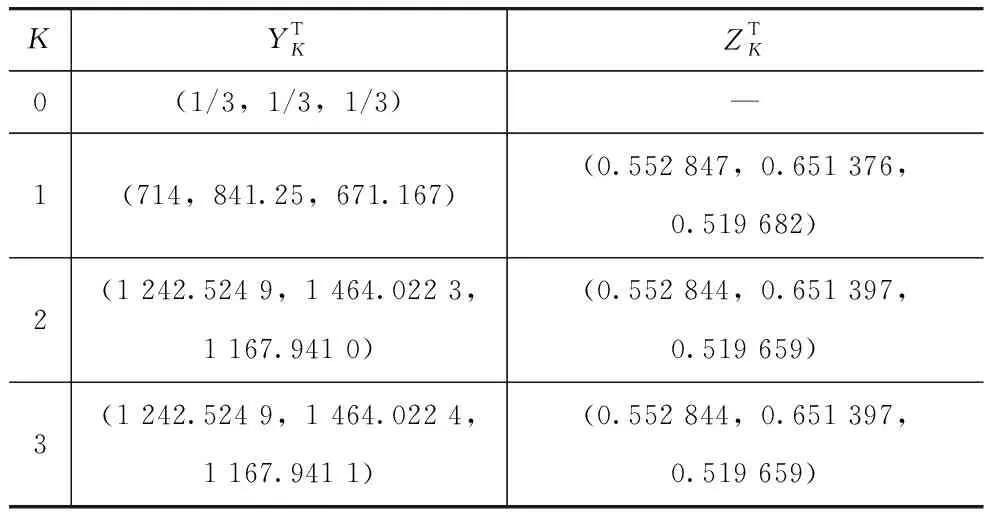
用群决策特征根法求得理想专家评分向量及目标名次(ε=0.000 003)。此方法只需将评分矩阵转置自乘记为矩阵F，该矩阵最大特征根对应的特征向量就是最优决策结论。与AHP法(层次分析法)相比，该方法无须另求两两权重比较的判断矩阵，因此更为精炼。由表1评分结果，可得采用数值代数中的幂法迭代计算出X*，各次迭代结果见表2。

(9)

当K=0时，Y0=(1/n,1/n,…,1/n)T∈En，Y1=FY0，Z1=Y1/‖Y1‖2

(10)

当K=1,2,3时，YK+1=FZK；ZK+1=YK+1/‖YK+1‖2

(11)

从最后一列查出，X*=(0.552 844,0.651 397,0.519 659)T，N*=(2,1,3)。

2.2.2 评标专家可靠性

将X单位化得

代入式(3)～式(6)，计算结果见表3。

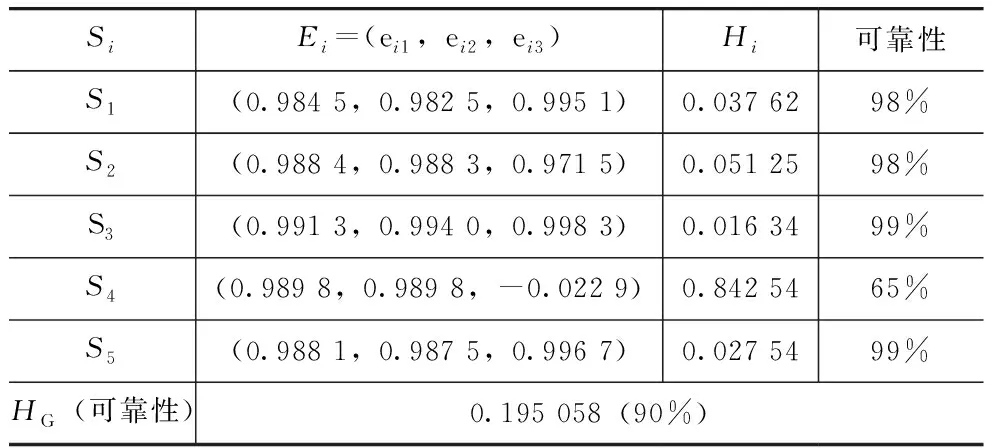
表3 计算结果表

由以上结果可以看出，专家S4的决策水平相对较低，影响了整个评价结果的准确性。由于S4可靠性较低，可在综合该标段评标结果时适当降低该专家的权重。

3 结语

本文从群决策问题出发，借鉴决策熵的测度思路，分析了评标专家可靠性评价的思路及原理，并构建了量化评标专家决策水平的计算模型。该方法计算简便、指标意义明确、实际可操作性强。尤其是在电子化评标系统应用后，通过系统平台积累的大量历史数据资源，将使得可靠性评价具有更好的时效性、连续性和科学性。