变步长LMS算法及在数字预失真中的应用*

云 涛

（中国电子科技集团公司第十研究所，四川 成都 610000）

0 引 言

业界对功放行为模型进行了大量研究，提出了许多简单高效的预失真模型，如Wiener[1]、Hammerstein[2]、GMP[3]和DVR[4]模型等，并在民用通信领域取得了极大成功，但是研究预失真参数提取的文献相对较少。文献[5]指出用一组样条基函数来代替多项式函数，不仅可增强模型拟合能力，而且提高了参数求解的稳定性；文献[6]指出通过线性插值和外推可减少待求参数个数，以降低参数求解的资源开销；文献[7]指出通过频率选择性压缩采样可降低计算量。以上文献介绍的参数提取方法大多基于数据块，不利于FPGA实时处理，收敛时间在秒量级。文献[8]提出利用LMS算法求解预失真参数。LMS算法要求不同时刻的输入信号向量线性无关。不满足该条件时，LMS算法的收敛速率将会变慢、跟踪性能变差。

对预失真参数快速提取问题，本文提出了一种自适应变步长的随机梯度下降算法（ALMS）。该方法利用参考信号和误差信号的指数加权移动平均（EWMA），自适应调整迭代步长，提高了收敛速率，同时降低了稳态波动。

本文安排如下：首先介绍广义记忆多项式模型和基于样条基函数的化简，其次详细分析最速下降算法的迭代步长和收敛性之间的关系，再次介绍ALMS的原理和实现，最后给出归一化LMS和ALMS收敛时间和性能的对比。

1 数字预失真

1.1 预失真训练架构

数字预失真训练架构分为直接和间接训练架构。间接训练架构首先求取功放失真模型，再求逆得到预失真模型。然而，求逆过程不仅消耗计算资源，也因求逆精度存在性能损失。而直接训练架构直接求解功放的逆模型，省去了求逆过程，性能更优，架构如图1所示。

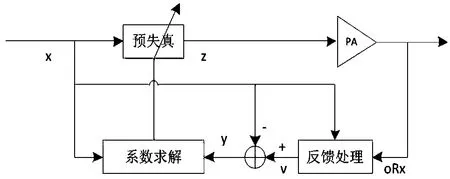
图1 直接训练架构

图1 中，x为预失真输入，z为预失真输出，oRx为功放耦合输出，v为经反馈处理和x对齐后的失真信号，y=v-x为误差信号。

1.2 预失真模型

本文采用广义记忆多项式模型：

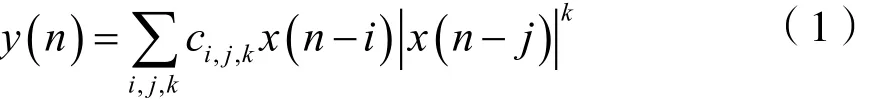
其中k表示非线性阶数，i和j分别表示信号延时和幅度延时，ci,j,k表示多项式系数。直接按照式（1）进行预失真会消耗大量的乘法器资源，且高阶多项式条件数大，系数求解不稳定。对式（1）进行适当变换，先对k求和得到：

其中fp为样条基函数，为对应基函数系数，w为参数矢量，u为x和fp生成的模型输入矢量。

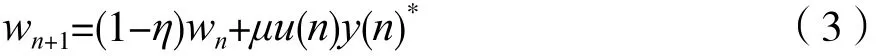
LMS迭代公式如下：其中，η=μγ为泄露因子，γ为正则化因子，μ为迭代步长。

1.3 收敛分析

设wo=R-1up为维纳解，相关矩阵Ru=E[uuH]，互相关向量p=E[ux*(n)]。令偏差εn=wn-wo，带入最速下降迭代公式，整理得到：

εn+1=(I-μ(Ru+γI))εn（4）矩阵Ru+γI特征值分解为VΛVH，其中：

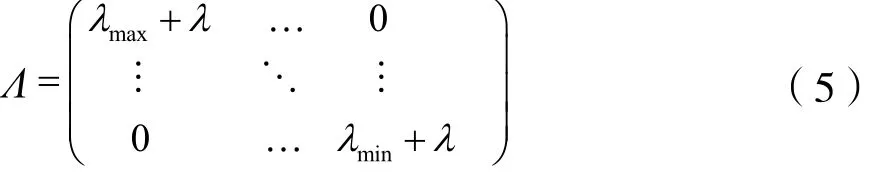
λi为矩阵Ru的特征值。带入式（4）并令bn=VHεn，整理得到：

为了保证迭代算法的收敛性，要求 |1-μ(λi+γ)|＜1对所有i均成立，且收敛速度最快的步长为：

从图2可以更好地理解式（7）。

主要结论如下：

（1）当 μ∈(0,2/(λmax+γ))时，可保证迭代算法的收敛性；

（2）当 μ*=2/(λmax+λmin+2γ)时，收敛速度最快；一般有 λmax≫γ≫λmin，有 μ*≈2/λmax，区域 1 长度远大于区域2长度；

（3）根据小步长统计理论，在统计意义上，以上结论对LMS仍然成立。

1.4 ALMS算法

从章节1.3的分析可看到，在区域1内，步长μ越大，收敛速度越快，但随机扰动也越大，造成预失真后发射底噪抬升。此外，μ*由λmax决定，而λmax由Ru决定。为了利用上述关系，可以建立模型输入u、误差信号y和步长μ之间的映射关系。当

自相关ru(0)较小或误差较大时，用大步长；当ru(0) 较大或误差较小时，用小步长。

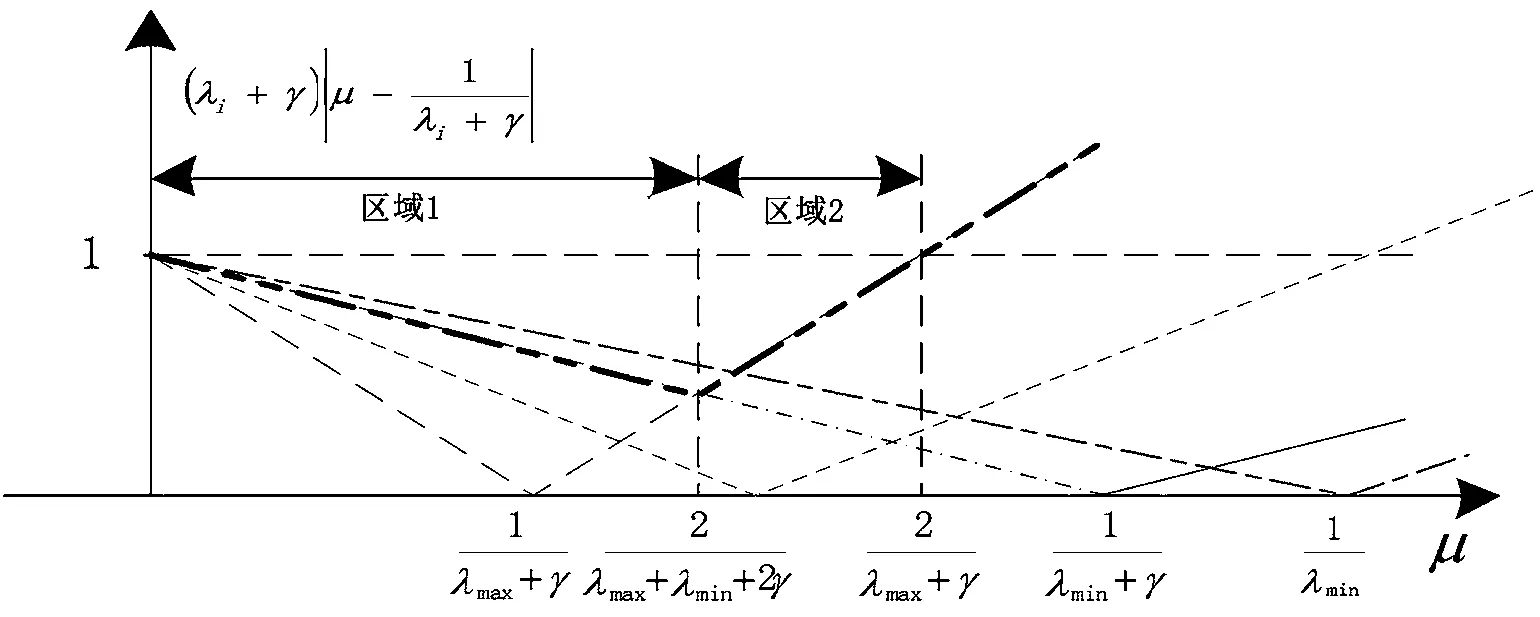
图2 SGD收敛分析

本文采用指数加权移动平均（EWMA）对ru(0)和误差信号功率p(n)进行实时估计：

β1和β2为可调参数，可在响应速度和估计性能之间折中选取。

ALMS迭代公式为：

式中，迭代步长的调整同时考虑了模型输入功率和实时误差功率，并用EWMA代替了瞬时估计，提高了归一化LMS算法的收敛速度和稳定性。此外，采用对数函数log2对和进行预处理，可避免除法运算，便于FPGA实现。

2 实测结果与分析

本文基于xilinx zc706和AD9371开发dpd算法，对比归一化LMS和ALMS算法的收敛时间和稳态性能。测试功放为U频段AB类功放，dpd模型采用11个查找表，dpd建模速率和反馈速率均为245.76 MHz，测试信号为10 MHz的OFDM信号，信号中心频点350 MHz。测试358 MHz处的100 kHz带宽内信号电平分析收敛时间，收敛时间定义为从启动迭代到达稳态性能减3 dB的时间。测试方案如图3所示。

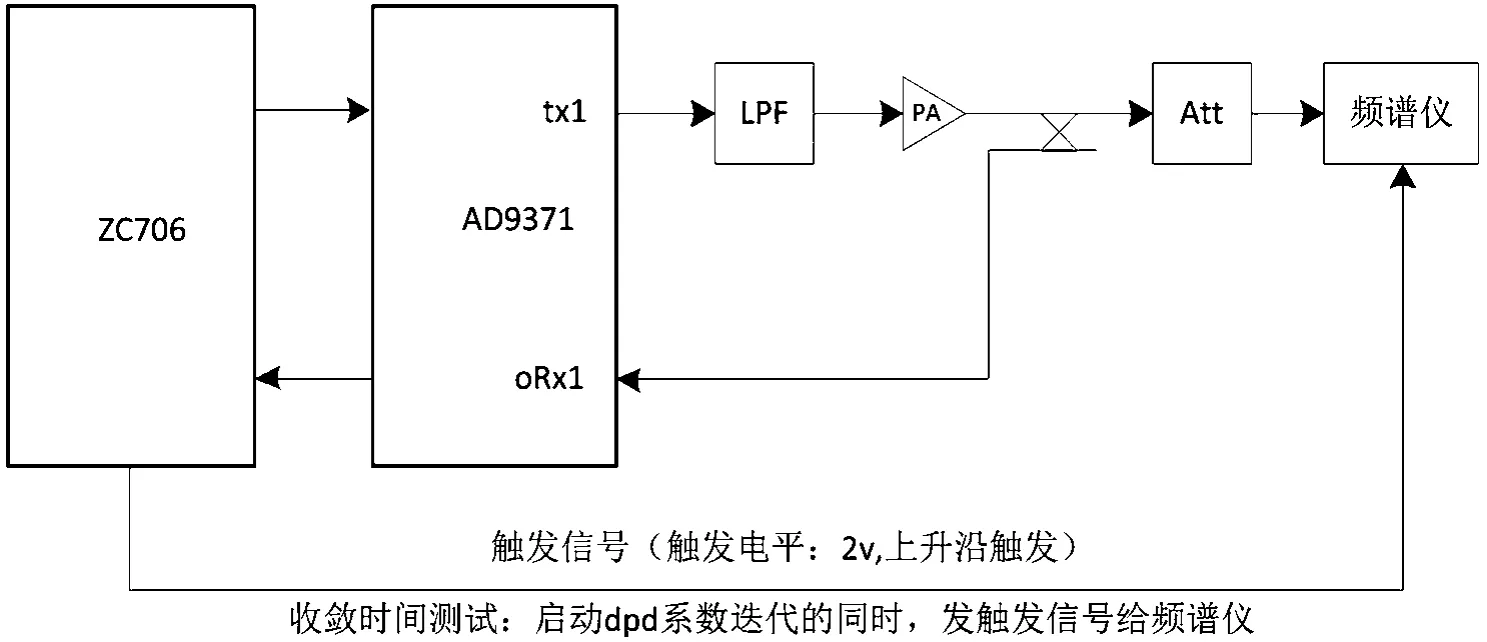
图3 测试方案

测试结果如图4、图5所示。测试结果的具体指标，如表1所示（注：μ=1/2mu）。

从图4可得出，本文提出的ALMS算法的稳态性能和小步长mu=24一致。相对大步长mu=18，底噪改善约5 dB。从图5可看到，ALMS的收敛时间相比小步长大幅缩短，逼近大步长收敛时间。综上，ALMS在稳态性能和收敛时间之间取得了较好平衡。

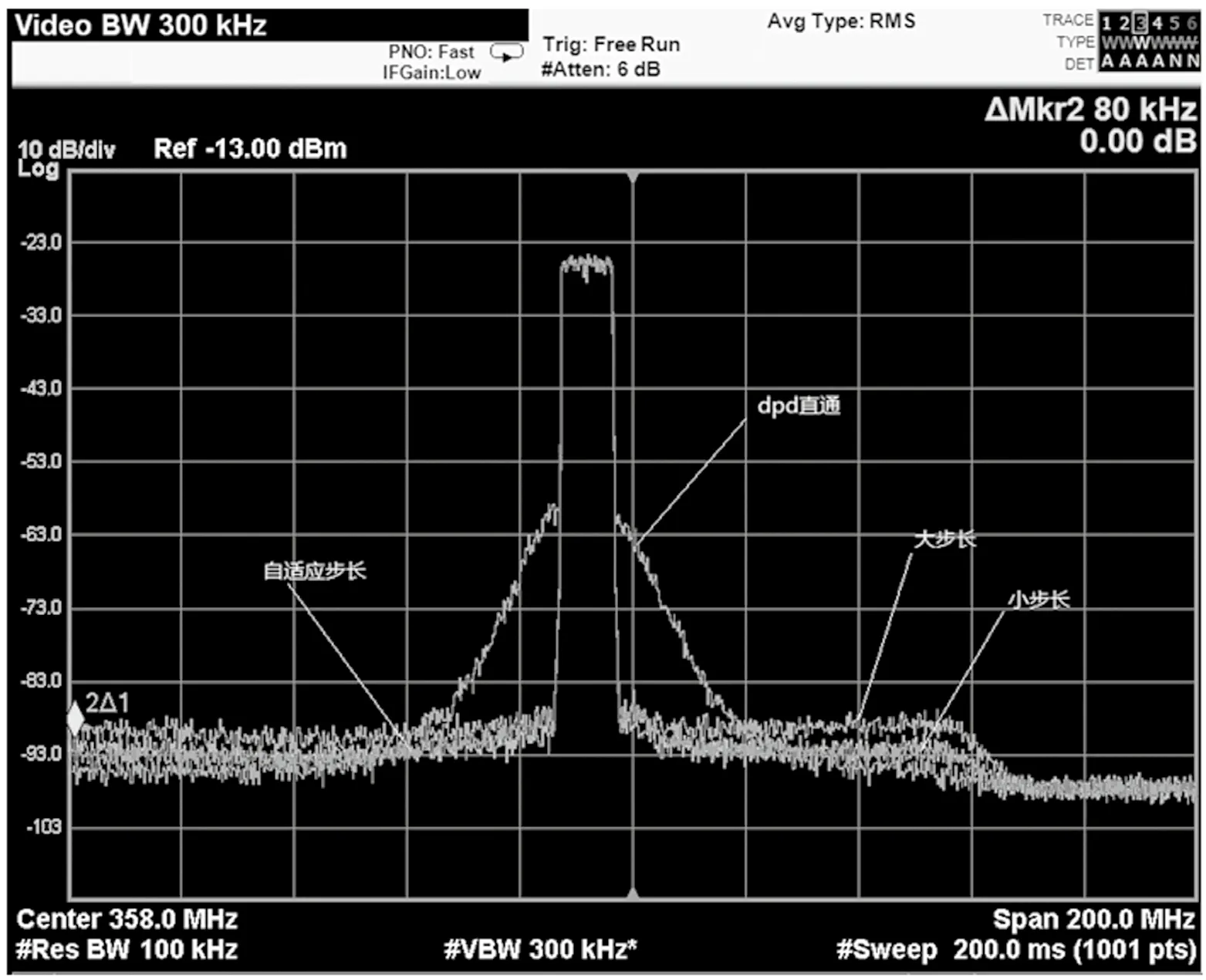
图4 稳态性能对比

图5 收敛时间对比

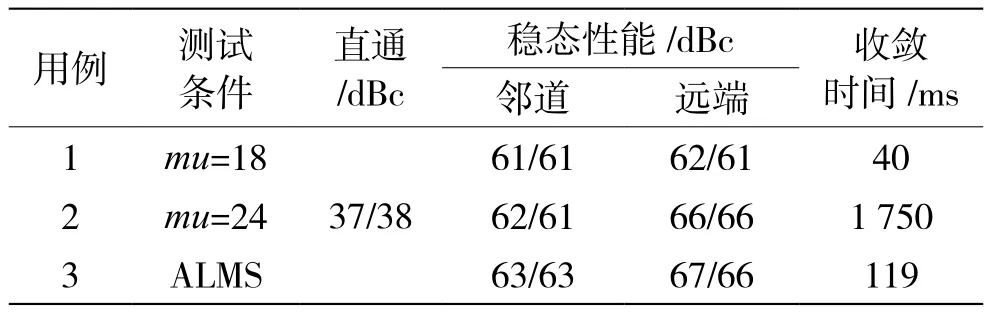
表1 测试结果

3 结 语

本文提出根据输入模型信号和误差信号的EWMA自适应变步长LMS算法，进一步缩短了归一化LMS算法收敛时间，同时降低了稳态波动，优化了算法的跟踪性能。最后，通过两组对比试验，证明了算法的有效性。