基于MATLAB的运动模糊图像恢复
黄宇涵,李德龙,李德富
(山东科技大学 电子通信与物理学院,山东 青岛 266590)
0 引言
由于人眼的特性,我们在观察物体的运动过程时,都是短时间内模糊的画面[1]。运动模糊是由成像设备运动或拍摄目标的运动引起的。成像设备的运动形成全局性的运动模糊图像,由于曝光时间很短,在曝光时间内成像设备的运动可近似认为匀速直线运动[2]。
1 模型原理
1.1 非局部均值法去噪
图像中往往伴随着程度不同的噪声干扰,所以在对图像进行复原时应先对图像进行去噪处理,获得质量更高更清晰的图片。
非局部均值去噪算法的原理就是在整个图像的范围内寻找相似度高的像素,换而言之,当我们在处理一个像素点时,都要进行它与图像中其他像素点间的相似度的计算[3]。为了提高效率,通常我们会选取两个大小固定的窗口:搜索窗口(D×D,D=2*Ds+1)和邻域窗口(d×d,=2*ds+1)。邻域窗口在搜索窗口中不断地移动来判断像素的权值[4]。
1.2 PSF参数的估计
如图3,对运动模糊来说,PSF主要包括两个参数,一个是模糊长度L,另一个是模糊角度θ。模糊长度是指一个像素点由于运动导致模糊的轨道范围,模糊角度是指由于运动导致图像模糊的方向[5]。
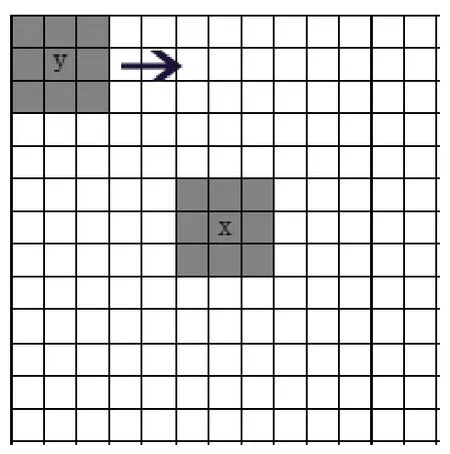
图1 算法执行过程Fig.1 Algorithm execution process

图2 对图像进行非局部均值滤波,去除噪声Fig.2 Non-local mean filtering of images
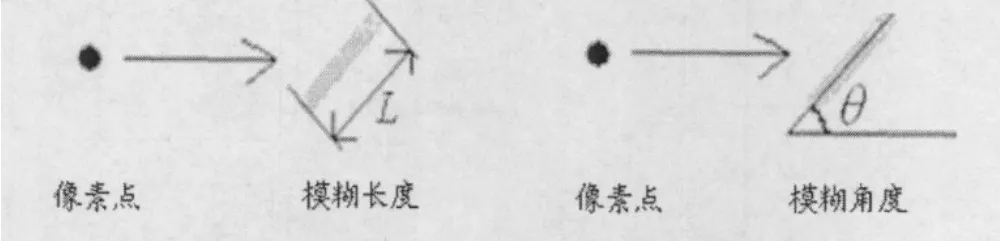
图3 运动模糊PSF的两个参数Fig.3 Two parameters of PSF with motion blur
成像时由于抖动导致景点和像点相对运动,其方向和速度是随机不定的,所以无法用系统分析的方法来推导PSF函数,用后验估计方式进行图像盲复原成为必须要做的工作。所以MBIR一般步骤:第一步是求解线性不变退化模型h(x,y),第二步骤是根据g(x,y)和h(x,y)来复原出逼近f(x,y)的估计图像,y)[6]。更加具体地说只要先估计出PSF中模糊长度L和模糊角度θ,就能进一步利用图像去卷积技术来复原图像。
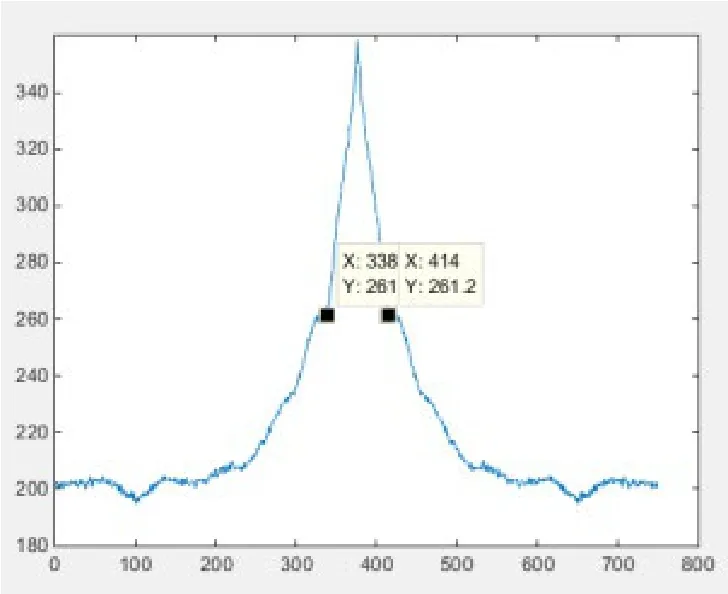
图4 对图像的模糊长度进行估算Fig.4 Estimates the fuzzy length of the image
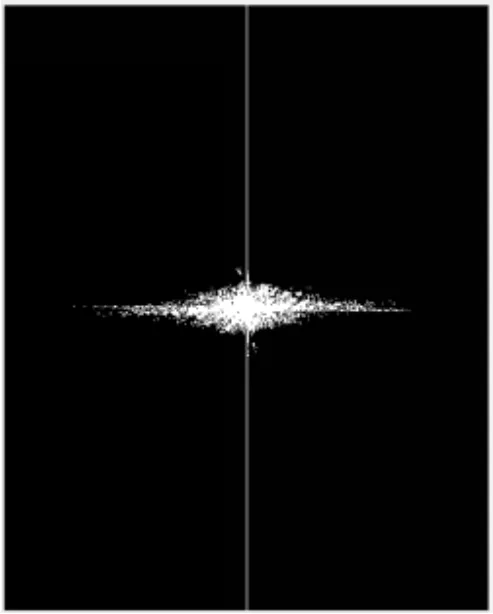
图5 对图像的模糊角度进行估算Fig.5 Estimates the fuzzy Angle of the image
1.3 有约束复原
在进行图像的恢复时,我们通常给复原增添一些适当的约束条件,在这些条件的约束下让准则函数达到最小,这类方法叫做有约束复原,而我们就是使用了有约束复原中的维纳滤波法[7]。维纳滤波法也叫最小均方误差滤波法[8]。它建立在图像和噪声都是随机过程,图像和噪声不相关,二者之一的均值为零,灰度估计值与退化图像中的灰度值呈线性关系的前提下。基本思想是找到原图像的一个估计值x,y),即
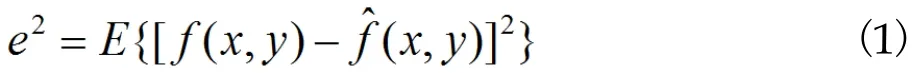
上式中E{}代表数学期望。设p(x,y)是维纳滤波器的复原函数,则复原图像(即原图像的估计值)可表示为

代入(3)式得

将上式对p(x,y)求偏导并令结果为零,可得到
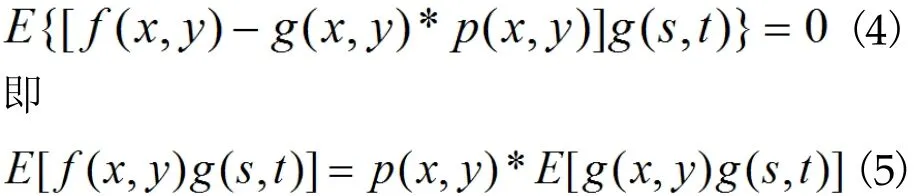
解出其中的p(x,y),使得上式达到最小的最优解。再将(5)改写为
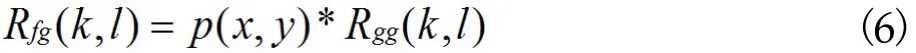
由卷积定理和功率谱密度定义,进行傅立叶变换得

所以维纳滤波器的复原函数为

最后得到维纳滤波器的复原滤波函数为
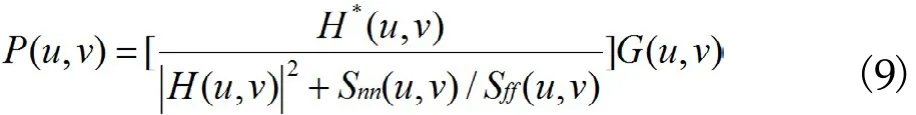
所得到的图像估计值在频域的表达值
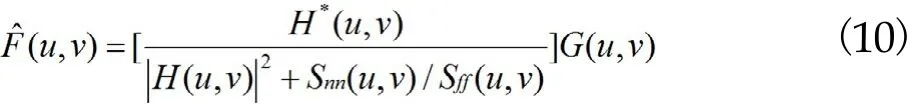

图6 维纳滤波Fig.6 Wiener filtering
2 结论
维纳滤波的缺点在于最优标准是基于最小均方误差的且对所有误差等权处理[9],这个标准在数学上可以接受,但却是个不适合人眼的方式,原因在于人类对复原错误的感知在具有一致灰度和亮度的区域中更为严重,而对于出现在暗的和高梯度区域的误差敏感性差很多。其次,空间可变得退化不能用标准的维纳滤波方法复原,而这样的退化是常见的[10]。最后,维纳滤波不能处理非平稳信号和噪声。

