灰色预测法在混凝土损伤层厚度预测中的应用

李 伟， 白 竞， 莫 诎， 邓冰杰

(1.中国十九冶集团有限公司， 四川 成都 610031； 2.重庆交通大学 土木工程学院， 重庆 400074； 3.重庆交通大学 河海学院， 重庆 400074)

混凝土的耐久性往往与其所处的环境有关，在诸如力学、化学以及物理等环境作用下，混凝土的耐久性将会呈现出逐渐或者骤然下降的趋势，尤其是那些处于盐渍土、严寒、近海与海域等地区的混凝土，其结构破坏比较严重，表现为受到硫酸盐侵蚀、干湿交替、荷载作用而导致混凝土发生膨胀、开裂、强度下降等现象。根据资料显示，在我国沿海地区和西部盐湖地区的土壤中，以及海水、地下水和温泉水中均含有大量的硫酸盐，处于硫酸盐环境与水位变动区、浪溅区及潮汐区的混凝土结构，在干湿交替和硫酸盐侵蚀的共同作用下，混凝土劣化程度更加严重[1-4]。

对于混凝土在硫酸盐-干湿交替双因素作用下的研究，大多数都是基于膨胀率、质量、动弹性模量、强度以及微观结构变化等方面而展开的[5-9]。而由混凝土受硫酸盐侵蚀机理可知，硫酸盐环境中的侵蚀离子与混凝土中水泥胶凝基体反应生成具有膨胀性的侵蚀产物，最终导致混凝土细观结构产生缺陷，由表及里形成损伤层[4]。因此，可以将混凝土损伤层厚度作为体现其损伤程度的一个重要衡量指标。

目前，混凝土损伤厚度基本都是利用超声平测法通过室内试验来计算的，但要想得到各种试验条件下混凝土损伤厚度，往往需要较长时间，尤其是在干湿交替作用下混凝土侵蚀前期阶段，混凝土的损伤并不明显，其损伤层也就无法准确测量计算。文献[4,10]在经过210、240、270、300、330、360 d后才对混凝土损伤厚度进行测量计算，其试验周期长达1年，研究滞后不言而喻。倘若想得到在390、420、450 d时间后的混凝土损伤层厚度，还需等待半年之久，这给研究带来十分不便。如果在不影响试验大致结果的前提下，能找到一种既可缩短试验周期又能近似地表达出试验结果的方法，将会大大提高研究效率。为此，本文将灰色预测法引入到混凝土研究中，从混凝土损伤层厚度这些数据出发，建立起灰色预测模型。

1 灰色预测法

灰色预测是指对既含有已知信息又含有未知或不确定信息的系统进行预测，即对在一定范围内变化的、与时间有关的灰色过程的预测[11-12]。通过鉴别系统因素之间发展趋势的相异程度(关联分析)，对原始数据进行生成处理，以便找到系统变化规律，最后，利用生成有较强规律性的数据序列建立起微分方程模型，从而预测事物未来发展趋势的状况。

为更好地对灰色预测法进行描述，这里首先给出灰色预测法的预测大致步骤：

(1)对原始时间序列进行数据处理；

(2)计算模型参数，建立微分方程，得到相应的灰色预测模型；

(3)对灰色预测模型进行残差检验、关联度检验以及后验差检验；

(4)对灰色预测模型进行修正，得到修正后的灰色预测模型；

(5)利用修正后的灰色预测模型进行相关预测。

下面对灰色预测步骤中所涉及的一些理论、公式以及实现等进行详细说明。

1.1 生成列

由于原始时间序列的随机性，我们在建立灰色预测模型前，往往要对原始时间序列进行数据处理，得到生成列以便找到数的规律。而这种需找数的方法通常有三种形式，即累加生成、累减生成以及映射生成，但限于篇幅且加之本文只用到累加生成，因此，以下只对累加生成进行描述。

所谓累加生成，是指通过数列间各时刻数据的逐个累加得到新的数据和数列。累加之前的数列为原始数列，累加之后的数列为生成数列。现设原始时间序列为

X(0)=[X(0)(1)，X(0)(2)，…，X(0)(n)]，

生成列为

X(1)=[X(1)(1)，X(1)(2)，…，X(1)(n)]，

则累加生成列公式为

(1)

1.2 灰色预测模型建立

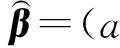
(2)

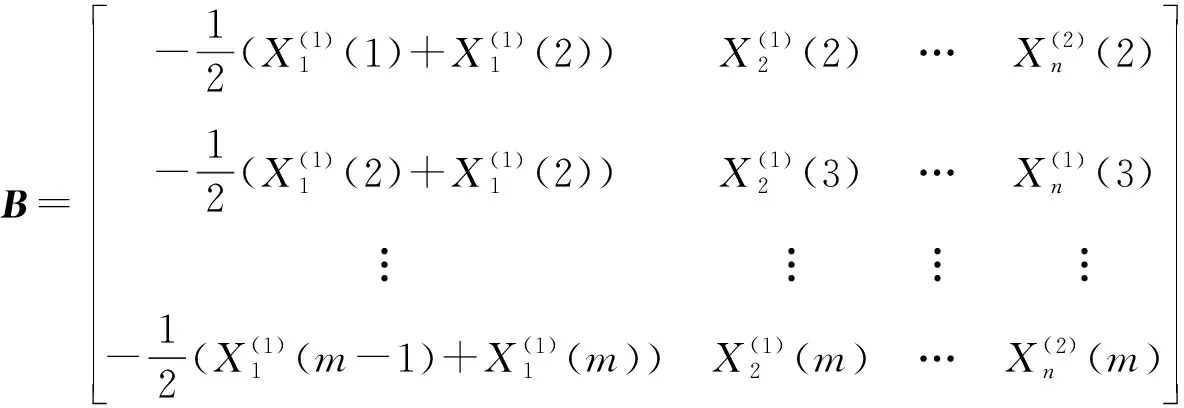
接着，建立微分方程：

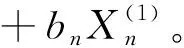
(3)

最后，建立灰色预测模型GM(1,n)：

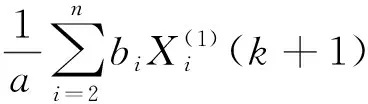
(4)

当n=1时，GM(1,n)模型为GM(1,1)模型，即为

，k=0,1,2,…,m-1。

(5)

1.3 灰色预测模型检验

1.3.1 残差检验

残差检验是指对模型预测还原值与实际值的残差进行逐点检验。残差检验组成部分包括绝对残差序列、相对残差序列以及平均相对残差。

绝对残差序列：

，i=1,2,…,n，

(6)

相对残差序列：

(7)

平均相对残差：

φi。

(8)

1.3.2 关联度检验

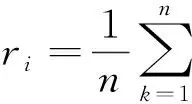
(9)

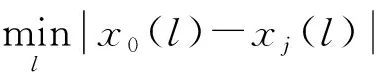
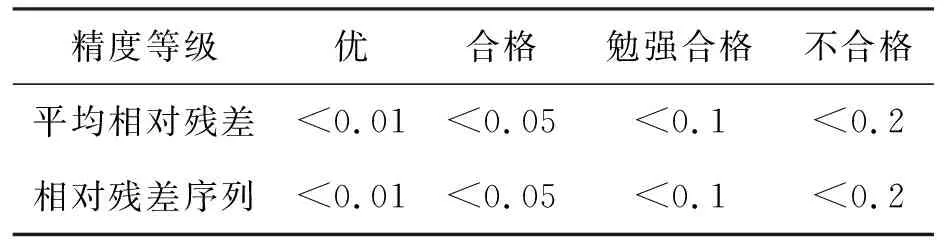
表1 精度检验表

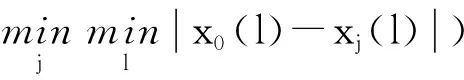
1.4 灰色预测模型修正

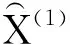
设残差序列为

E(0)={ε(0)(k0),ε(0)(k0+1),…,ε(0)(j),…,ε(0)(n)}，

(10)

，

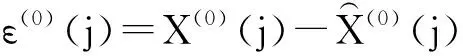
(11)

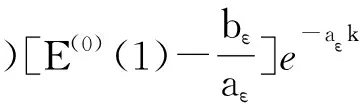
2 预测实例

现有4组不同配合比的混凝土试件，在不同浓度的硫酸钠溶液(Na2SO4)、不同水胶比以及不同损伤龄期条件下，分别对这4组混凝土试件进行试验。试件制作、试验方法与方案、混凝土损伤层厚度的测试原理及方法等参见文献[4,10]，而混凝土配合比汇总于表2[4,10]，利用超声平测法测得的损伤层厚度汇总于表3[4,10]。

表2 混凝土配合比

表3 混凝土损伤层厚度

由于试验研究的是在单因素(不同水胶比或者不同浓度Na2SO4)条件下混凝土损伤层厚度变化情况，因此，采用GM(1，1)模型对表3中质量分数10% Na2SO4条件下不同水胶比以及0.45水胶比条件下不同质量分数Na2SO4的损伤层厚度值进行预测，预测内容包括：

(1)何种情况下，对混凝土损伤层厚度影响最大；

(2)预测在390 d时间后，处于质量分数10% Na2SO4条件下，随着水胶比变化的混凝土损伤层厚度值；

(3)预测在390 d时间后，处于0.45水胶比条件下，随着Na2SO4质量分数变化的混凝土损伤层厚度值。

以下给出灰色预测的MATLAB实现过程，并由伪代码形式进行表达：

(1)clear；输入表3中的原始数据X0。

(2)利用公式(1)产生累加生成列cumsum(X0)。

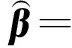
(4)for m=1：length(X0)-1；按式(6)—(9)进行残差检验与关联度检验。

参照表1，如果经计算所得的平均相对残差、相对残差序列中最后一位值以及关联度分别满足小于0.05、0.05、0.6的要求，则预测模型合格，此时可以进行下一步预测；否则，将按式(10)—(11)进行预测模型修正。

如果经计算所得的平均相对残差、相对残差序列中最后一位值以及关联度分别满足小于0.05、0.05、0.6的要求，但精度不是很理想时，此时也可以按式(10)—(11)对预测模型进行修正。

(5)for k=1，2，...，n(对任意时间点)；根据步骤(3)或者(4)所得到的预测模型进行预测。

(6)输出结果

根据MATLAB计算得到不同条件下的关联度(如表4所示)以及在质量分数10% Na2SO4与0.35水胶比情况下，第360 d的混凝土损伤层厚度16.035 3 mm，这与表3中的16.05 mm只相差0.014 7 mm，说明灰色预测是可行的，因此，继续对390 d时间后的混凝土损伤层厚度进行预测，预测结果如表5所示。同时，由表4可知在质量分数10% Na2SO4与0.35水胶比情况下的关联度最高，达到0.615 4，这说明该情况下对混凝土损伤层厚度影响最大。

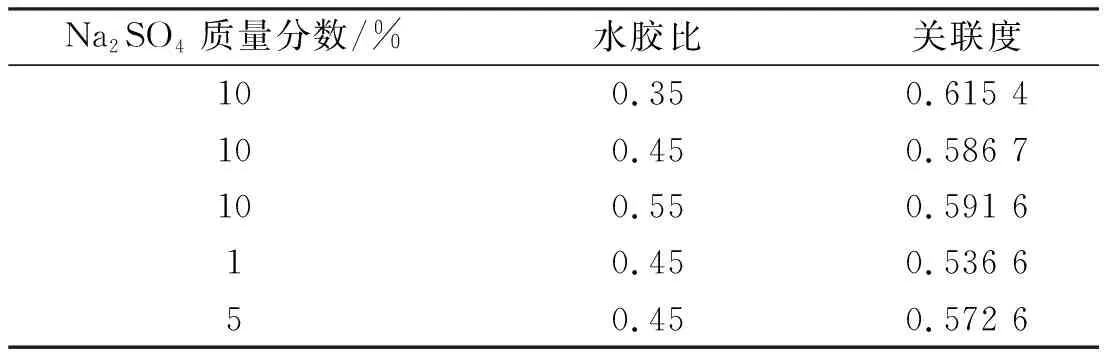
表4 不同条件下的关联度

表5 390 d混凝土损伤层厚度预测结果

此外，可以从表5中看出，在质量分数10% Na2SO4与0.55水胶比情况下，混凝土在390 d时间后的损伤层厚度为22.884 7 mm，达到最大，且比相同条件下360 d时间后的损伤层厚度高出1.584 7 mm，这也符合文献[4]中混凝土损伤层厚度随水胶比增大而增大的规律，即在相同质量分数Na2SO4下，水胶比越高，其混凝土内部的孔隙将会更多，由此导致在Na2SO4溶液侵蚀作用下盐析加快，进而加速破坏混凝土，使得混凝土损伤层厚度逐渐变大。同时，结合表3和表5可知，不同损伤龄期(时间)对混凝土损伤层厚度的影响较大，损伤龄期越大，凝土损伤层厚度越大，以质量分数1% Na2SO4与0.45水胶比为例，在该条件下，混凝土损伤层厚度随着不同损伤龄期增大而增大，这和文献[10]的试验结果一致。

3 结 论

混凝土损伤层厚度是研究混凝土耐久性的一个方面，由于混凝土耐久性问题本身就比较复杂，完全采用试验手段来达到研究目的，虽然可以实现，但其周期过长。而灰色预测法可以较好地解决这个问题，为研究混凝土损伤层厚度影响问题提供重要的理论支持，不失为一种可以借鉴使用的方法。同时，预测实例证明了灰色预测法的可行性，将其应用于未来试验结果预测中，能够近似地计算出试验结果，因此，值得推广使用。