小学数学几何直观教学的实践与思考
黄益彬
(南靖县山城中心小学,福建 南靖 363600)
数学课堂上合理运用几何直观进行教学,可以生动形象地展现数学问题的本质,提高学生的思维能力和分析能力。教师在教学中应合理运用几何直观,帮助学生理解概念和算理、利用线段图直观理清数量关系、鼓励学生画规范的示意图、个性草图构建几何表象。
一、利用画图直观表征,促进学生理解概念
认知心理学认为:概念形成其实可以概括为两个阶段,即从完整表象上升为抽象概念,实现抽象概念在思维过程中的具体再现。小学生的思维正处于具体形象思维向抽象思维过渡,更要通过直观教学,引导学生从大量的直观图形中形成丰富的表象,然后抽象出概念。特别是有些概念特别抽象,学生不易理解,让学生用语言进行描述与交流比较困难。这时,教师应让学生画出直观图形,表达出自己构建的概念表象,与同学交流,促进学生对概念的理解。
例如:人教版三年级上册“倍的认识”教学片段:
1.引发与旧知识冲突,初步认识倍的概念
(1)课件出示例题情景图:胡萝卜2根红萝卜6根
师:胡萝卜的根数与红萝卜的根数有什么关系?
小结:根据学习经验,可以比较出这两个量谁多谁少。
师:你们能换一种新的比较方法吗?(引发与旧知识冲突,寻找新的比较方法。)
课件演示:把2根胡萝卜移到一块排成一行圈成1圈,把六根红萝卜移到一块排成另一行平均分成3份,每2根圈起来。
生:胡萝卜有1份 红萝卜有3份
生:胡萝卜有2根 红萝卜有6根
师揭示倍的概念:像这样胡萝卜2根,红萝卜有3个2根,我们就说红萝卜的根数是胡萝卜的3倍。让同桌互相说一说。
接着课件出示:唱歌2人、跳舞6人;红花2朵、黄花6朵;苹果2个,梨6个等大量存在3倍关系实物素材,让学生用眼睛看一看,在心里圈一圈,初步感知倍的含义,与“几个几”建立起联系。最后课件演示去掉素材中的实物,留下两组集合圈表示一个数是另一个数的“3倍”关系。
首行○ 次行○○○
借助这组图示,把两个量之间的倍数关系转化成图形之间的关系,让学生直观理解倍的关系。
2.在变化中,及时类比,凸显倍的本质,加深对“倍”概念的理解
(1)改变几倍数
师:胡萝卜数不变,增加一个2根红萝卜,两个2根红萝卜,3个2根红萝卜。(指导学生画出线段图表示出它们的倍数关系)
小结:胡萝卜2根,红萝卜有几个两根,就是红萝卜是胡萝卜的几倍。
(2)改变一倍数,再次通过让学生画图直观理解倍数
师:现在胡萝卜又多了一根,红萝卜还是6根,动手圈一圈。
师:红萝卜还是2根2根圈一起吗?
倍的概念涉及两个量之间的比较,十分抽象,不易学生理解,在学习过程中,通过以上一系列“变与不变”的对比活动,学生圈一圈、画一画,借助集合图、线段图,运用不同的图式表征出倍的概念的本质特征,建构倍的直观模型,促进学生对概念的深度理解。
二、利用数形结合表征,引导学生借形思数理解算理
在小学数学教学中,数形结合是一种重要的思想方法,低年级教材主要以实物图、实物操作的形式呈现,画图表征策略相对隐性。因此,可以根据教学内容,引导学生依托“形”去思考“数”实现“实物图—示意图(直条图)—线段图”的过渡递进。如“求一共有多少朵花?”由实物直观向几何直观的过渡(见图1):
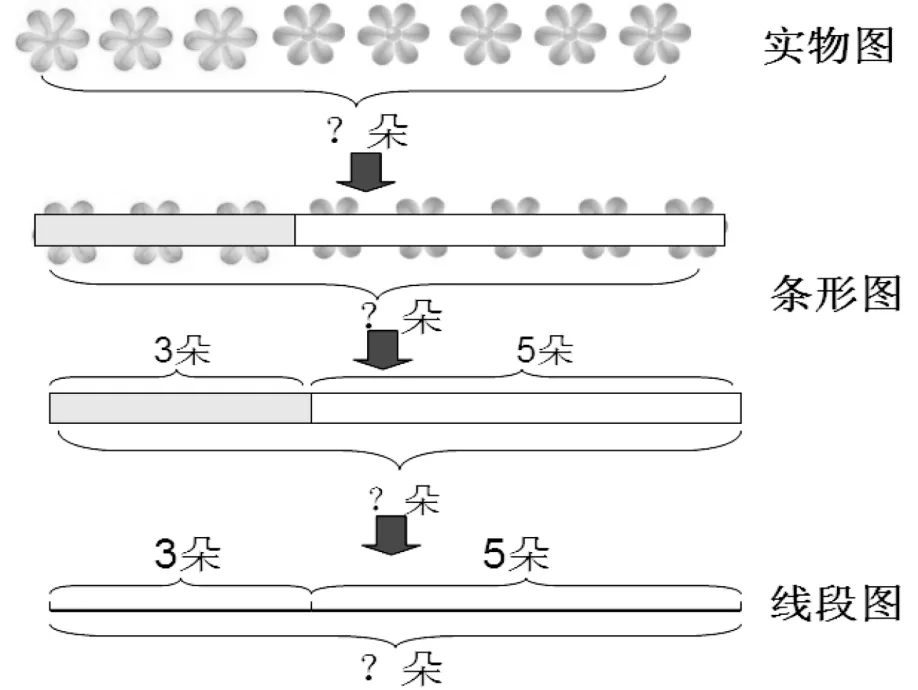
图1
实物图的图示过程就是描绘的过程,是小学生真实的几何直观的起点阶段,但是这不是教学中的目标;直条图是用几何图代替实物,从实物图向直条图过渡中,给学生渗透了为什么表示3朵花的直条比表示5朵花的直条短,这时学生从具体形象思维向抽象逻辑思维跨越了一大步;最后从直条图过渡到线段图,关键要让学生明白:可以根据需要,一个长度单位表示任意的量,但线段间的长短与两数之间的大小关系一定要相匹配,比如3朵花的线段一定要比5朵花的线段短,而线段到底画多长,不是本质。
需要注意的是,在低年级的教学中,不能只停留在直观图形的分析上,而要及时地引导学生从直观图形提升到数学思考的层面上来。例如,一年级上册“9+几”这一课,可以通过五个层次帮助学生理解和掌握“凑十法”。一看——课件演示”凑十“的过程;二摆——自己实践,动手操作“凑十”;三想——闭上眼睛回忆操作凑十的过程;四说——说出用”凑十“法计算9+4的过程;五填——在算式下面注出用”凑十“法计算的过程。“看”和“摆”是在积累“凑十”数学经验,“想”和“说”是从数学经验中建构“凑十”的数学模型,“填”的过程就是学生数学思考的过程。通过这五个步骤的教学,通过数形结合,引导学生由直观的操作过程过渡到用语言叙述的过程,最后到抽象的计算过程。
这样,通过教师有意识、有目的地示范,可以让低年级的学生感受几何直观的价值所在,为中高年级的学习做好铺垫。
三、利用线段图表征,帮助学生理清数量关系
线段图具有直观性、形象性,所以一直都是表征题目意思、分析数量关系、寻求解决问题策略的重要法宝。因此,要鼓励学生积极利用线段图去直观分析和解决问题,学会把复杂的数量关系转化为直观的线段图,理清复杂的数量关系,积累利用几何直观解决问题的经验。
例如:一套衣服共456元,上衣的价钱是裤子的2倍多6元。这套衣服的上衣和裤子各多少钱?通过调查,如果这道题仅从字面上去理解,四年级的学生只有8%左右能正确做出来。如果教师引导学生把题目的数量关系“抽象”成线段图(如下图),这样就把“上衣和裤子的价钱关系”转化成“两条线段之间的关系”,最后通过对线段图的分析,学生会恍然大悟:要求上衣的价钱,首先必须求出裤子(一份)的价钱,而要求出每份的价钱,应该知道3份的价钱是多少:456-6=450(元),裤子的价钱:450÷3=150(元),上衣的价钱:456-150=306(元)或者 150×2+6=306(元)。这样引导抓住关键句,画出线段图,直观感知1倍数,几倍数之间的对应关系,突出数量关系的分析,为学生解决问题提供强有力的直观支撑,形成解决问题的方法。

图2
四、利用几何直观,帮助学生建构空间观念
空间观念是指根据物体的基本特征抽象出几何图形,或根据几何图形想象出所描述的实际物体,想象出空间物体的方位和相互之间的位置关系,根据语言描述或通过想象画出图形等。学生空间观念的建立,需要实物感知经验和图式表象,借助几何直观可以把复杂的数学问题变得简明、形象,帮助学生建立几何表象、建立空间观念。
例如,“厘米的认识”的教学,如何帮助学生在头脑中直观地建立起1厘米的数学模型?可以借助直尺这一实物,先让学生在直尺上找出1厘米的长度,仔细观察后,闭上眼睛,记住1厘米的长度,初步建立1厘米的空间观念;再用手指比划1厘米的长度,加深对1厘米这一长度的建模;最后让学生找一找生活中哪些物体的长度大约是1厘米。通过这些活动,学生在头脑中建立了1厘米的长度概念,发展了空间观念。
再如,有这样一道习题:学校有一个长方形花圃,长6米,在修建花圃时,花圃的长增加了3米,宽增加了2米,这样花圃的面积就增加了27平方米,花圃原来的面积是多少平方米?学生读题后,教师问:“谁能解决这个问题?”由于本题数量关系比较复杂,光靠“读”题学生很难理解题目的意思,一时想不出解决问题的办法,教师适时提示:“想想可以用什么办法。把这些条件和问题用直观的方式表达出来?”学生产生了动手画图的需要。

图3
学生画图解答(见图3),
图形b的面积:2×3=6平方米
图形c的面积:2×6=12平方米
图形a的面积:27-6-12=9平方米
原来长方形的宽9÷3=3米
原来长方形的面积:6×3=18平方米
师:3米表示什么?
生:3米表示图a宽,也就是原来长方形的宽。
师:你是怎么知道的?
生:通过画图,从图上看出来的。
这次的追问,让学生对几何直观表征的价值有更加深刻的体验。

