一种基于模糊准则的发酵过程残糖质量浓度的预测方法

刘辉， 赵忠盖， 刘 飞

（江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122）

在发酵过程中，糖通常作为菌体生长的营养物质，是反应发酵进程的重要指标，因此需要对残糖质量浓度进行检测[1]。目前，一些先进的发酵过程采用生物传感器（例如美国YSI公司的YSI系列葡萄糖分析仪、瑞典Chemel AB公司的SIRE系列的的葡萄糖分析仪等）进行在线检测残糖质量浓度[2]，但由于其生物活性酶膜材料难以承受高温灭菌，且发酵罐内环境复杂，影响检测精度，因此需要将发酵液提取出来进行稀释、净化等处理，使发酵液满足生物传感器的检测条件。但是受流速、管道长度、体积等影响，提取过程缓慢，检测值存在较大滞后[3]，因此需要对残糖质量浓度进行在线预测。

目前大多数学者对残糖质量浓度预测问题的研究是利用软测量技术，将一些在线可测变量（例如pH、DO、滞后的残糖质量浓度等）来估计不可在线测量变量（例如残糖质量浓度等）[4]。基于机理模型的软测量，能较为全面的反映过程的本质[5]，但由于发酵过程的高度复杂性，难以建立残糖质量浓度的精确机理模型[6]。而基于数据建模的软测量，通过样本数据建立模型，进而估计残糖质量浓度，应用广泛[7-8]，但这种数据建模过度依赖训练数据，而发酵过程由于操作条件和环境等多因素影响，很难获得重复性好的实验数据，因而建立的模型适用性不强。发酵工艺人员在长期的操作实践中，积累了关于残糖质量浓度预测的大量经验知识，但这种以经验知识为基础的预测因人而异，预测效果差别很大。模糊预测算法则对经验知识进行总结并建立规则库来描述对象变化的趋势，在发酵过程中应用广泛[9-11]。

实际操作中，发酵工艺人员根据菌体生长耗糖的惯性特征，局部线性化残糖质量浓度曲线，假设前一段时间发酵罐中耗糖质量浓度变化量等于后一段时间的耗糖质量浓度变化量，进而设计了一种残糖质量浓度的经验估算算法，但是在残糖质量浓度变化较大的情况下，前一段时间耗糖质量浓度变化量并不等于后一段时间的耗糖质量浓度变化量，因此估算效果不好，误差较大。作者在分析和改进经验估算算法之后，结合预测控制思想[12]，采用反馈补偿校正方式，提出了经验估算改进（即有补偿）算法；此外，针对工艺人员的残糖质量浓度估算模型的不准确性，结合模糊智能技术[13]，进行模糊模拟，分别研究了模糊预测无补偿以及模糊预测有补偿，最后分别对上述4种算法进行仿真和现场实验验证对比，为滞后检测的残糖质量浓度估算提供了新途径。

1 发酵过程残糖质量浓度在线检测系统

菌体发酵补糖控制的工艺流程见如图1。粗线为管道，细线表示通信线，箭头表示信号或溶液的传送方向。通过恒流泵1提取发酵液，恒流泵2连接纯净水，两股液体按照一定的比例，在混合器中充分混合稀释，送入检测仪器进行在线检测，通过滞后检测值估算罐中残糖值，并将罐中残糖值送入PC机，PC机控制蠕动泵的开度，实现向发酵罐的补糖。发酵过程中，流加和发酵液的损失同时存在，为简化计算，假定补料前后发酵罐中发酵液的体积不变，设定滞后时间为 td，采样时间为 t，且 td=q*t，（q=1，2，3…）。

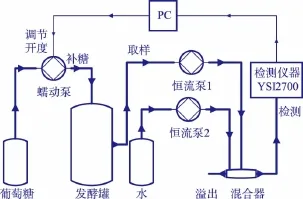
图1 菌体发酵补糖控制的工艺流程图Fig.1 Bacterial fermentation of sugar supplement control flow chart

2 残糖质量浓度经验估算算法

发酵工艺人员根据菌体生长耗糖的惯性特征，局部线性化残糖质量浓度曲线，假设前一段时间发酵罐中耗糖质量浓度变化量等于后一段时间的耗糖质量浓度变化量，进而设计了一种残糖质量浓度的经验估算算法。残糖质量浓度经验估算算法见图2。

假设td=3*t。设第时刻时，检测仪器YSI2700检测到滞后检测值Cn(i-3)，为估算此时发酵罐中的值C(i)，设第i-1到i时刻，补糖质量浓度变化率为F(i-1)，第i-2到i-1时刻，补糖质量浓度变化率为F(i-2)，第i-3到i-2时刻，补糖质量浓度变化率为F(i-3)，第i-3到i时刻，发酵罐中耗糖质量浓度变化量为 C耗i-3到i，如图 2（a）所示，则有：

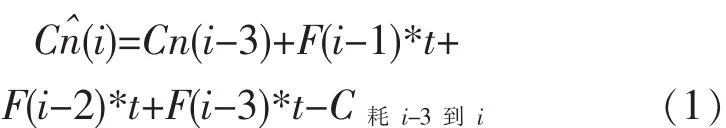
在公式（1）中，Cn(i-3)为滞后 检测 值，可 由YSI2700 检测得到，F(i-1)、F(i-2)、F(i-3)分别为 i-1、i-2、i-3时刻的补糖质量浓度变化率，容易得到，而C耗i-3到i为第i-3到i时刻内的耗糖质量浓度变化量，难以得到。

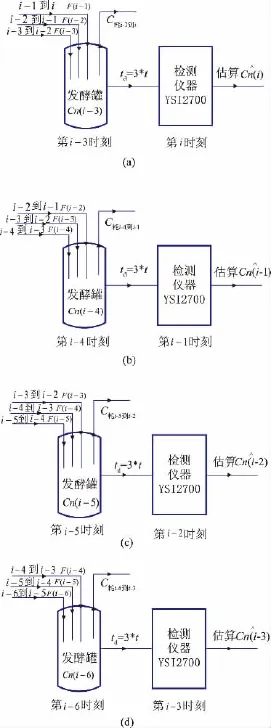
图2 残糖质量浓度经验估算算法Fig.2 Experience estimation algorithm of residual sugar concentration

为获得 C耗i-3到i，分析图 2（a）和（b）。 第 i-1 时刻时，检测仪器YSI2700检测到滞后检测值Cn(i-4)，可认为是第i-4时刻时发酵罐中的残糖质量浓度值。同理，第i时刻时，检测仪器YSI2700检测到滞后检测值Cn(i-3)，可认为是第i-3时刻时发酵罐中的残糖质量浓度值。针对发酵罐而言，在第i-4到i-3时刻，发酵罐中残糖质量浓度值从Cn(i-4)变为Cn(i-3)，则有：

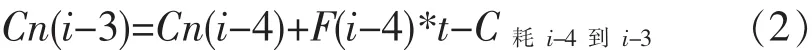
对公式（2）变形得公式（3）：

同理两两分析图 2（b）、（c）、（d）依次可以得到C耗i-5到i-4、C耗i-6到i-5，那么有：

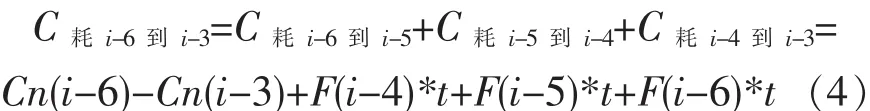
发酵过程残糖质量浓度（无补糖）大致曲线见图3。菌体生长过程大致分为缓慢期（0-A）、生长期（A-B）、衰亡期（B-C）[6]。 从菌体生长周期来看，残糖质量浓度曲线变化缓慢，可以认为：

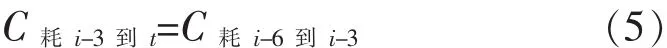
因此，综合上述公式得到公式（6），就能估算残糖质量浓度值。

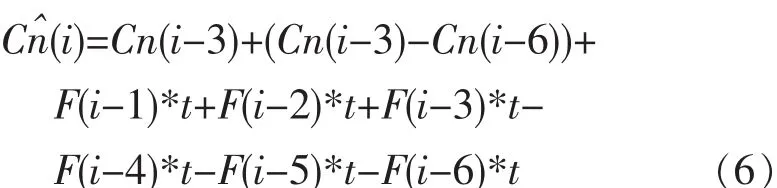
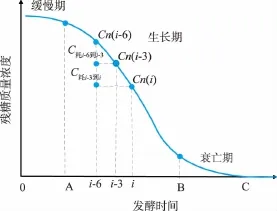
图3 发酵过程残糖质量浓度（无补糖）大致曲线图Fig.3 Graph of residual sugar concentration with no sugar supplement in fermentation

3 一种残糖质量浓度经验估算改进 （即有补偿）算法

公式（6）中补糖质量浓度变化率容易得到且为具体数值，因此为简化计算，假定补糖质量浓度变化率 F(i)=0，得公式（7）：

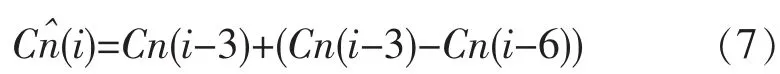
公式（7）中 Cn(i-3)、Cn(i-6)均可由仪器 YSI2700 测得，为方便分析，将公式（7）改写成Cn(i-3)的函数，即：

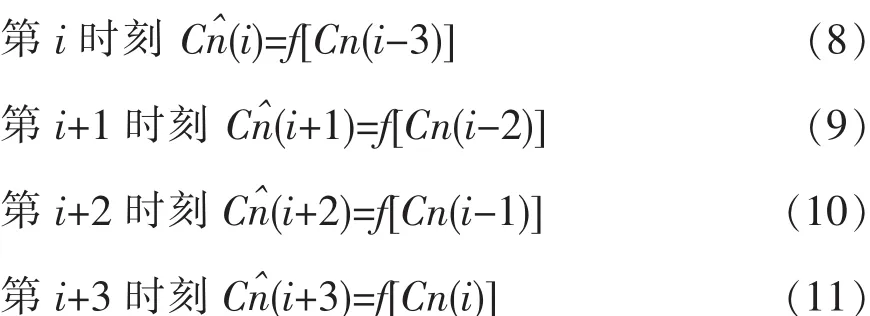
经验估算算法在假设公式（5）成立的前提下给出了残糖质量浓度的估算值。但是在实际情况中，残糖质量浓度曲线可能存在较大变化 （例如缓慢期、生长期以及衰亡期之间的过渡期；生长期曲线本身呈现指数下降形式等），公式（5）往往不成立，如果依旧采用公式（6）对残糖质量浓度进行估算，估算结果必然不准确，因而偏差较大。

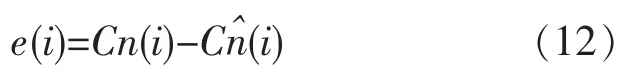
第i+3时刻

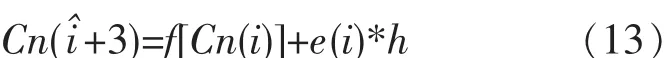
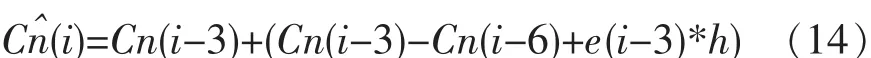
4 一种残糖质量浓度模糊预测算法

4.1 残糖质量浓度经验估算算法的模糊模拟

公式（6）在公式（5）成立的前提下给出了经验估算算法，可以认为公式（6）是残糖质量浓度的估算模型。由上述分析可知，公式（5）往往不成立，可以认为该估算模型不准确。为获得较为准确的估算模型，采用模糊知识来模拟残糖质量浓度估算模型。

Aoki等人[9]首次提出了一种模糊预测算法并将其成功应用于高炉熔融玻璃的温度控制中，Da[11]对模糊预测算法进行详细分析和总结，建立了输入为y（i）-y（i-1）、u（i）-u（i-L），输出为（i+L）的模糊预测器来估算（i+L），为模糊模拟残糖质量浓度估算模型提供了思路。其中 y（i）（i+L）表示 i时刻的滞后检测值、估算值，u（i）表示i-1时刻控制对象的输入，L表示滞后时间。

首先对公式（6）进行变形得公式（15）：

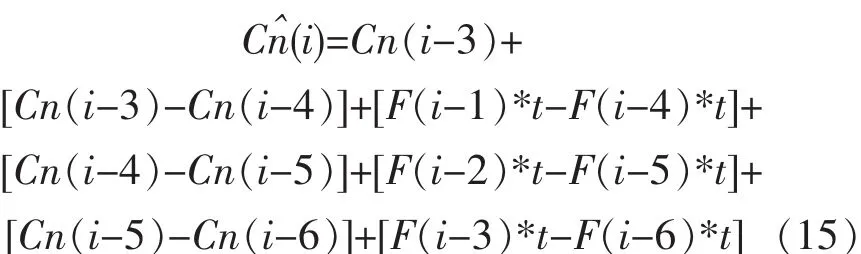
分析上式可知，符合Da的模糊预测思想，在此基础上，对公式（6）重新进行分析，可以建立输入为Cn（i-3）-Cn（i-6）、F（i-1）+F（i-2）+F（i-3）-F（i-4）-F（i-5）-F（i-6），输出为 δ（i-3）的模糊预测器来估算

4.2 残糖质量浓度模糊预测算法

为方便分析，首先定义公式（16）、（17）。

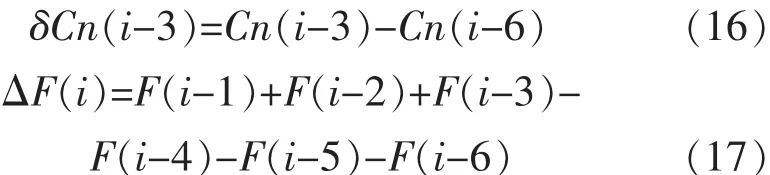
本文中，模糊预测无补偿算法包括以下两个步骤：

步骤一：（ΔF（i）、δCn（i-3））→δ（i-3）

第i时刻时，通过检测仪器可以得到滞后检测值Cn（i-3），以及i时刻之前的补糖质量浓度变化率，可以计算出δCn（i-3）和 ΔF（i），于是可以预测出滞后时间内的残糖质量浓度变化量δ（i-3），结合步骤二就可以得到估算值图4给出了i时刻时，给定 ΔF（i）为正大（PL）情况下，不同δCn（i-3）所对应的δ（i-3）的变化趋势。点画线表示残糖质量浓度变化缓慢，但仍存在小范围波动。

如果采用类似于模糊规则进行描述，可以得到如下三条规则：

Rule 1：if ΔF（i） is PL and δCn（i-3） is PB，then δ（i-3） is LL

Rule 2：if ΔF（i） is PL and δCn （i-3） is Z，then δ（i-3） is L

Rule 3：if ΔF（i） is PL and δCn（i-3） is NB，thenδ（i-3） is O

其中 PL 表示 ΔF（i）的变化 E 为正大；PB、Z、NB表示δCn（i-3）的变化 EC 为正大、不变、负大；LL、L、O表示δ（i-3）的变化Y为正大、正小、不变。

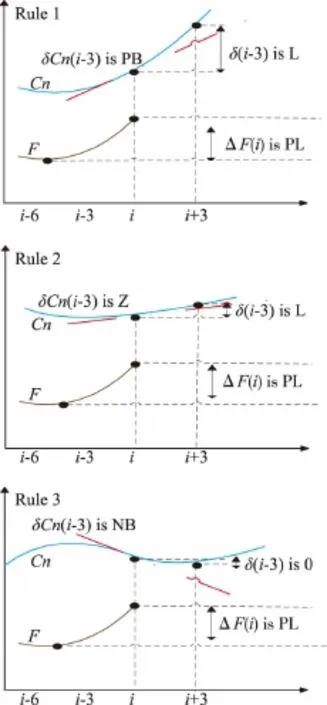
图4 残糖质量浓度模糊预测算法（ΔF（i）变化趋势为正大给定）Fig.4 Predictive algorithm of residual sugar concentration（change trend of ΔF（i） is PL given）

通过对 ΔF（i）、δCn（i-3）和 δ（i-3）的变化趋势进行分类和推断，可以得到表1所示的类似于模糊规则的预测规则库。结合上述分析可知，残糖质量浓度模糊预测有补偿算法仅需在模糊预测无补偿算法的基础上加上步骤三，即：

步骤一：（ΔF（i）、δCn（i-3））→δ（i-3）

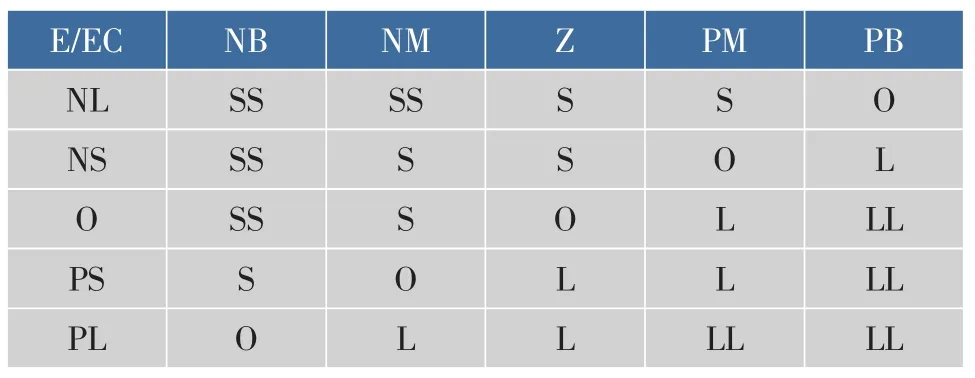
表1 模糊预测规则库Table 1 Fuzzy prediction rule base

5 仿真及实验研究

5.1 加水稀释实验

鉴于加水稀释仿真过程可控性好、透明性强、糖种类少、过程简单等特点，因此将上述4种方法应用于加水稀释仿真实验中，来验证上述理论的正确性与可行性。作者首先采用残糖质量浓度加水稀释模拟发酵过程进行仿真对比。仿真中，假设容器体积足够大，保证加水不会溢出；加水后溶液体积的变化等于加水前溶液的体积加上加水的体积，忽略分子间互溶作用。

设将18 g糖配置成1 L的糖水，采样周期为0.2 h，滞后时间0.6 h，仿真总时间为8 h，补糖质量浓度变化率 F（i）=0。0～1 h 内，通过调节加水流速使之满足于耗糖质量浓度变化量呈现缓慢增大趋势，模拟菌体生长缓慢期；1～5 h内，通过调节加水流速使之满足于耗糖质量浓度变化量呈现快速增大趋势，模拟菌体生长生长期；5～8 h内，通过调节加水流速使之满足于耗糖质量浓度变化量呈现快速减小趋势，模拟菌体生长衰亡期。图5给出了残糖质量浓度加水稀释模拟发酵过程的残糖质量浓度变化图。

图5 残糖质量浓度加水稀释模拟发酵过程仿真Fig.5 Simulation of residual sugar concentration by water dilution

由于补糖质量浓度变化率F（i）=0，因此在模糊预测中，忽略输入 ΔF（i），认为 ΔF（i）变化趋势始终为 O（不变），另一个输入 δCn（i-3）的基本论域为（-1.7，1.7），输出 δ（i-3）的基本论域为（-1.7，1.7），输入 δCn（i-3）和输出δ（i-3）的隶属函数选用图 6 所示的三角形。

图 6（a）中 EC 为δCn（i-3）的语言变量，NB（负大）、NM（负小）、Z（正好）、PM（正小）、PB（正大）分别与等级（-2、-1、0、1、2）相对应；图 6（b）中 Y 为δ（i-3）的语言变量，SS（负大）、S（负小）、O（不变）、L（正小）、LL（正大）分别与等级（-2、-1、0、1、2）相对应。根据上述分析，选用表1所示的模糊预测规则库。

清晰化过程中，作者选用公式（18）所示的最大隶属度平均值法，其中u表示最大隶属度，n表示最大隶属度的个数。

为方便比较，定义经验估算算法为经验估算无补偿算法、经验估算改进算法为经验估算有补偿算法。仿真过程中，分别运用经验估算无补偿算法、经验估算有补偿算法、模糊预测无补偿算法、模糊预测有补偿算法对残糖质量浓度进行估算。图7给出了4种估算算法下的残糖质量浓度对比图。表2采用如公式（19）所示的绝对误差积分准则即IAE性能指标来进行定量比较，IAE越小，估算的精度越高。

从图7可以看出，在1 h时，模拟菌体从缓慢期到生长期，由于滞后作用，模糊预测有补偿算法在1.6 h时曲线有明显下降趋势，同样，在5.6 h时，有明显上升趋势，表明模糊预测有补偿算法估算下的残糖质量浓度曲线能够较好的区分缓慢期、生长期和衰亡期。此外，相比其他3种估算算法，模糊预测有补偿算法估算下的残糖质量浓度曲线更接近真实曲线。从表2中的IAE指标定量来看，模糊预测有补偿算法下的IAE最小，表明估算结果相比其他3种算法更为精确。

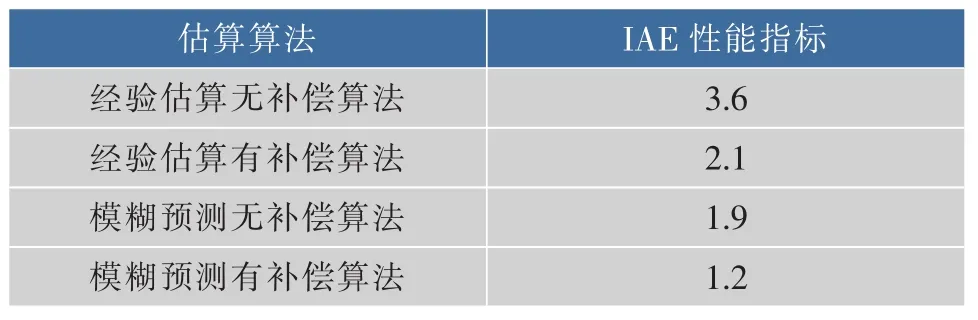
表2 IAE性能指标评价Table 2 IAE performance evaluation

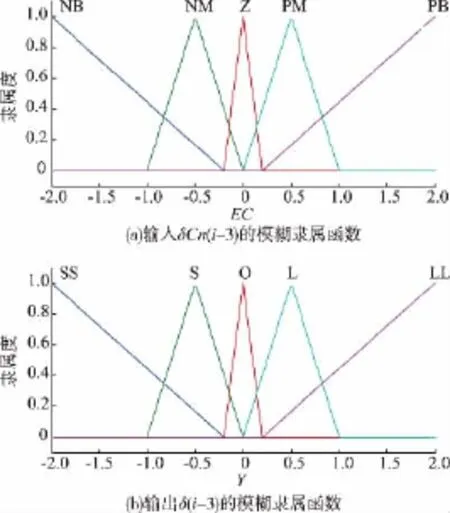
图6 输入 δCn（i-3）和输出 δ（i-3）的模糊隶属函数Fig.6 Fuzzy membership function of input δCn（i-3） and output δ（i-3）

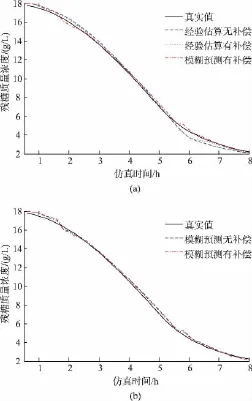
图7 仿真实验对比图Fig.7 Simulation results comparison

5.2 发酵过程残糖质量浓度实验

为验证上述方法的实用性以及模糊预测的优越性，将上述4种方法应用于蛋白酶发酵实验中。实验中，YSI2700的采样周期0.1 h，滞后时间0.3 h，仿真总时间为6.3 h，补糖质量浓度变化率F（i）=0。

模糊预测算法中设定δCn（i-3）的基本论域为（-1，1），输出 δ（i-3）的基本论域为（-0.5，0.5），此外选取图6所示的隶属函数，表1所示的模糊预测规则，式（18）所示的清晰化公式。

实验过程中，同样分别运用经验估算无补偿算法、经验估算有补偿算法、模糊预测无补偿算法、模糊预测有补偿算法对残糖质量浓度进行估算。图8给出了4种估算算法下的残糖质量浓度对比图。受检测仪器、人工操作等影响，残糖质量浓度波动较大，设在i-3时刻时，得到估算值，并在 i时刻时通过仪器检测到真实值Cn（i-3），并且有）；设当 i时刻，经验估算无补偿得到，并且有，如果采用经验估算有补偿算法，则必有图 9 所示的，从而使得估算效果变差。

从图7中可以看出，上述这种情况普遍存在，因而采取补偿算法反而使得估算效果不好，因此在实验过程中，最终选取经验估算无补偿算法和模糊预测无补偿算法进行实验比较。表3给出了这两种算法下的IAE性能指标对比。

图8 残糖质量浓度实验对比图Fig.8 Experiment results comparison of residual sugar concentration

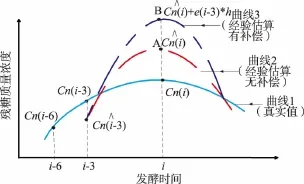
图9 补偿过程分析Fig.9 Compensation process analysis

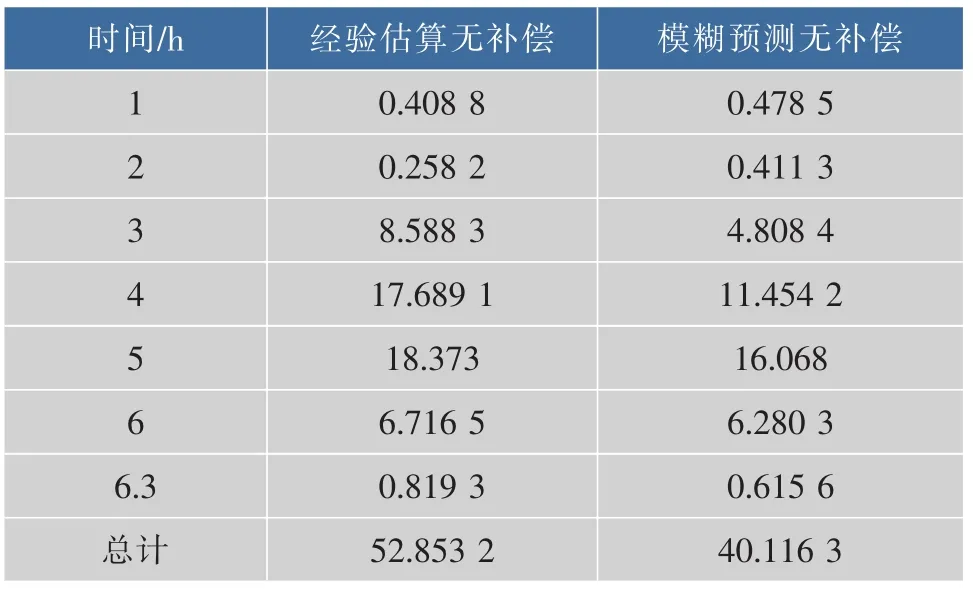
表3 IAE性能指标评价Table 3 IAE performance evaluation

菌体发酵大概分为缓慢期、生长期和饱和期。从图 8（c）中可以看出，0～2 h内菌体处于缓慢期，耗糖较少，残糖质量浓度缓慢变化，采用经验估算无补偿和模糊预测无补偿都能较好的估算残糖值。2～6 h内菌体处于生长期，耗糖较多，受实验环境、人工操作等影响，残糖质量浓度产生较大波动，采用模糊预测无补偿的效果好于经验估算无补偿。6 h以后，菌体进入衰亡期，耗糖变少，残糖质量浓度变化也较小，经验估算无补偿和模糊预测无补偿也能较好的估算残糖值。表3中各阶段的IAE性能指标表明模糊预测算法能够有效减小估算误差，提高精度，好于经验估算无补偿算法。

6 结 语

作者在分析经验估算算法之后，针对实际情况中，前一段时间耗糖质量浓度变化量并不等于后一段时间的耗糖质量浓度变化量，结合预测控制思想，采用反馈补偿校正方式进行改进，提出了经验估算改进（即有补偿）算法；此外，针对工艺人员的残糖质量浓度估算模型的不准确性，结合模糊智能技术，进行模糊模拟，分别研究了模糊预测无补偿以及模糊预测有补偿，最后分别对上述4种算法进行仿真和现场实验验证对比。仿真结果表明，模糊预测有补偿算法明显好于其他3种算法，但是在实际实验过程中，受检测仪器、人工操作等影响，采用补偿方式，估算效果稍差于无补偿方式，但是模糊预测无补偿的效果还是好于经验估算无补偿，表明模糊预测能够较好的建立残糖质量浓度的估算模型，提高精度，为滞后检测的残糖质量浓度估算提供了一种新的方法。