小实验 大玩场
——“有趣的三门问题”教学设计与反思
□ 朱雪莲 饶大燕 执笔
在一次教师培训中,笔者有幸聆听到蔡金法教授的讲座,他在讲课过程中给学员们呈现了一个数学经典问题——“三门问题”,组织大家采用小组合作方式开展研究。学员们对形成“换门”“不换门”“投币”的解决策略没有疑义,但由于问题的正确结果和解题者的直觉反应有着很大的差异,引起了大家的争议。回到学校后,笔者对这个问题一直怀有浓厚的兴趣,虽然可以通过百度查询到结果,但是久久没有找到一个能说服自己的解题办法。
一、实验解读
三门问题(MontyHallproblem),亦称为蒙提霍尔问题或蒙提霍尔悖论,出自美国的电视游戏节目Let'sMakeaDeal。参赛者会看见三扇关闭了的门,其中一扇门的后面有一辆汽车,选中后面有车的那扇门可赢得该汽车,另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门,但未去开启它的时候,节目主持人开启剩下两扇门的其中一扇,露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是:换另一扇门是否会增加参赛者赢得汽车的概率?
面对这个问题,直觉告诉人们:如果被打开的门后什么都没有,这个信息会改变剩余的两种选择的概率,哪一种都只能是二分之一。显然,这是一个概率论和人的直觉不太符合的例子,这告诉我们在做基于量化判断的时候,要以事实和数据为依据,而不要凭主观和直觉来决定。我们可以从合情推理或通过计算得出相应的概率。
推理过程如下:如果参赛者选择了一扇有山羊的门,主持人必须挑另一扇有山羊的门;如果参赛者选择了一扇有汽车的门,主持人随机在另外两扇门中挑一扇有山羊的门。我们可以遍历所有可能,那么假设参赛者选择1号门,就会存在三种可能情况:
A.参赛者选择汽车,主持人选择山羊甲,转换失败。
B.参赛者选择山羊甲,主持人选择山羊乙,转换成功。
C.参赛者选择山羊乙,主持人选择山羊甲,转换成功。
可见转换选择后的成功概率为三分之二。
计算过程如下:使用数学工具贝叶斯公式。我们用事件A代表参赛者第一次选择的门后是汽车,B代表主持人打开的门后是山羊。那么已知B的情况下,A发生的条件概率P{A|B}用贝叶斯公式可得:

二、实验目标
拟通过1个课时的“三门问题”探究学习,达成以下学习目标:
1.知道什么是“三门问题”,通过猜想、推测、实验、分析,初步理解不换门、换门、投币三种策略赢得汽车的概率,培养学生的统计素养。
2.培养学生勇于猜想、积极合作、大胆求证、观察分析等的科学研究精神。
3.通过联系生活,学生感受数学与生活的密切联系,感受数学的价值。
三、实验过程
(一)“要不要换门”——创设实验情境,激发认知冲突
【教学片段一】

师:看明白了没有?看明白的同学简单地复述一下游戏规则。
生:就是有三扇门,三扇门后各藏有一件奖品,两件是山羊,一件是汽车。猜奖者任选一扇门并得门后的奖品。在猜奖者当场选定一扇门未打开前,主持人打开了另外一扇门,发现后面是羊。
师:这时,你打算怎么办?
生:坚持原来的选择。
生:改猜另一扇门。
生:投一枚硬币,正面朝上选择不变,反面朝上改猜另一扇门。
【环节点评】
富有趣味性的学习内容,使学生产生探究的兴趣与欲望。通过让学生观看综艺节目微视频的形式导入新课,数学游戏内容丰富且直观,又含有较高的思维含量,让学生对“三门问题”产生浓厚的学习兴趣。在猜奖者当场选定一扇门未打开前,主持人打开了另外一扇门,发现后面是羊。教师抛出问题:“这时,你打算怎么办?”在实验模拟情境中,有效唤醒了学生已有的统计知识经验,引发学生的认知冲突。
(二)“换门的胜算大吗”——大胆猜想,试析引发实验需求
【教学片段二】
师:同学们,现在出现了三种策略,你觉得哪种策略获得汽车的概率更大?
生:我觉得三种策略的可能性都是一样的,都是三分之一。
师:你的猜测非常大胆,谁还有不同的想法?
生:我觉得不一定是三分之一,因为策略三换门和不换门的概率是不一样的。如果你抛到正面,正面是不换门,反面是换门,那么换门的概率会更大一些。
师:你有不同的意见,你觉得这三个哪个是有问题的?
生:抛硬币。
师:那抛硬币的概率应该是多少?
生:我觉得抛硬币的概率应该是二分之一,硬币有两个面,随便抛一个就是正面或反面。
生:我认为三个都是二分之一,因为最后剩下的都是对换门和不换门这两种情况进行选择。
师:你们都很会猜想,三种策略赢得汽车的可能性分别是多少?怎么办呢?
生:就和原来解决抛硬币、摸乒乓球的问题一样,做个数学实验吧。
【环节点评】
每个人都有猜想的潜能,当一个人的思维被激活,迫切地想知道某个问题的答案时,往往都会先进行猜想,以满足自己求知的欲望。所以在抛出问题“哪种策略获得汽车的可能性更大”时,一下子就激发了学生的学习热情和积极性,让学生产生主动猜想的欲望。同时,教师创设了一个良好的课堂氛围,学生根据自己的理解提出猜想,在对话交流中拓宽了解决问题的视野,从而获得解题的思路,提出做数学实验的需求。我们也发现,在研究一个新的数学问题时,不可能总有先例可供参考,这时就需要大胆地发挥猜想,突破原有的桎梏,敢于实践求知。而宽松和谐的课堂氛围能使学生的思维活跃,多元、新奇的猜想才可能出现,点燃学生创新学习的火花。
(三)“哪种胜算更大”——经历实验过程,验证实验猜想
【教学片段三】
1.实验前制订实验规则。
师:既然要做数学实验那就应该有规则,你觉得要注意些什么?
生:主持人应做到保密、公平,不能提前泄露汽车在哪儿。
生:主持人自己要对汽车心中有数,随机选择汽车。
生:做实验时,实验的次数尽量要多一点,实验会更加准确。
师:我们是否要先确定小组成员,想一想小组成员有几人?
生:需要一个主持人和一个猜奖者。
师:除了主持人、猜奖者还可以增加,你们觉得还可以增加哪些成员?
生:观察员、记录员,帮忙记录结果和监督……
2.实验中需要注意的事项。
师:我们用三个纸杯代替三扇门,分别在纸杯底部写有“车”“羊”“羊”字样,反过来放在桌面上。在做实验过程中,还应该注意什么呢?请同学们观看一段模拟视频。
生:实验纸杯要一模一样。
生:不能在三个纸杯上做记号,否则会影响实验结果。
生:每次猜完,主持人要调换纸杯的位置,猜奖者要遮住眼睛不能偷看。
生:猜奖者心态要好,不要一个劲地想得到汽车,影响可能性大小。
师:是的,实验过程中,实验者的态度影响着实验结果,赢得汽车不是我们的最终目的,探究三种策略哪种获得汽车的可能性最大,才是我们的研究目的。我们用纸杯代替门,虽然研究条件简陋,但只要我们遵守实验规则,结果仍然有效。
教师介绍实验单使用方法。
2号实验单
实验换门策略赢得跑车的可能性 实验员( )
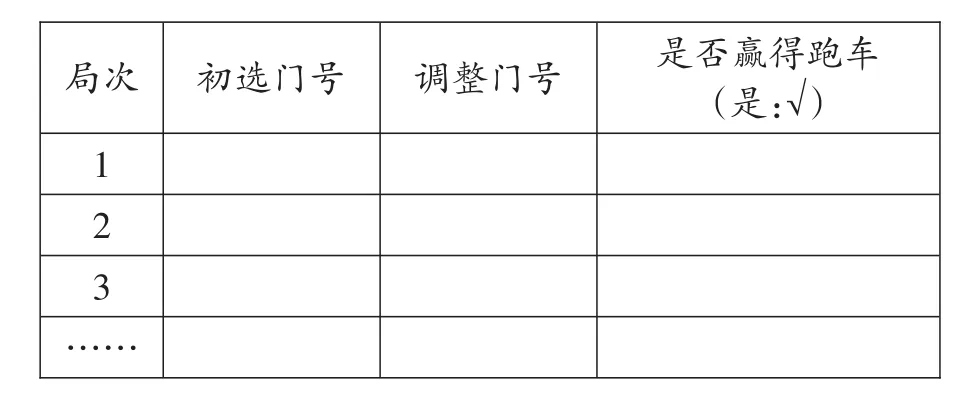
局次初选门号 调整门号 是否赢得跑车(是:√)1 2 3……
实验结果统计如下:
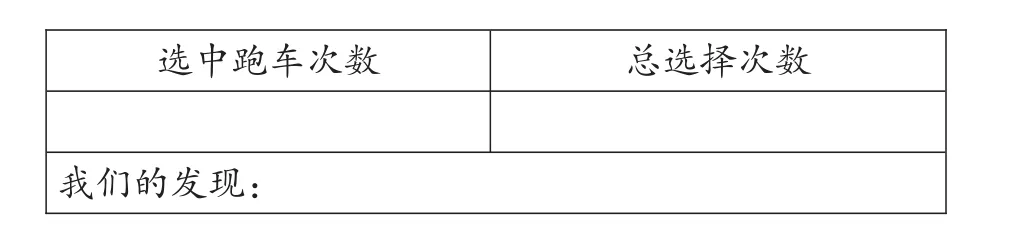
选中跑车次数总选择次数我们的发现:
师:考虑到策略3硬币容易滚落,所以建议采用投币策略的同学,可以多领一个纸杯,用手掌盖住杯口,充分摇动杯中硬币。
3.自由组合实验小组。
根据每个学生选择的最想参与的实验策略,调整学生座位,自由组合实验小组并领取实验材料。
【环节点评】
在实验探究过程中,我们设置了开放型的探究活动,即学生自己制订实验过程的注意事项,自主选择喜欢的一种策略做实验,自主确定同伴的人数和小组成员的分工,真正把课堂变成人人参与、个个思考的空间。在做实验过程中,每个小组的记录员及时记录猜奖者的实验结果,是获得羊还是汽车。选择不换门策略的小组会很快发现,当猜奖者做出第一个选择之后,主持人打开了山羊这扇门,猜奖者再次做选择这个环节其实是无效的,所以实验过程只需要前半程即可。选择换门策略的小组也会在实验中顿悟,第一次选择山羊的结果肯定是赢得汽车,山羊对应两扇门,所以赢得汽车的可能性大。这些实验的临场感悟,为学生更好地理解实验现象背后的缘由打下了基础。
(四)“为什么要换门”——比较辨析明理,探索实验缘由
【教学片段四】
1.借力实验数据,质疑猜想。
(学生进行汇报,汇报后师生一起统计总次数、选中次数,计算选中百分比)
师:请同学们比较一下我们最初的猜测和实验数据,你想说什么?
生:差得很多,换门的和抛硬币的两种概率。
师:你想说的是这两个数据比我们猜测的要高很多,是吗?
生:我们猜测是二分之一,但实际是32.5%,感觉有点奇怪。
师:也就是它和谁比较接近?三分之一。
生:我们一开始以为三种策略的概率是一样的,但是发现原来换门的概率最大,其次是抛硬币。
生:我发现其实换门和不换门的就是互补的,加起来是“1”,如果不换门的概率小那么换门的概率必然大。
师:现在这些实验数据出来了,你觉得准确吗?
生:可能不太准确。

图1 三门问题板书图
2.借力样本数据,完善猜想。
师:只凭这几组数据,我们能验证自己的猜想了吗?
生:我们做的实验次数还太少,实验结果可能还不够准确。
师:那现在我们就增加实验的次数,进一步验证猜想。(样本数据演示)
师:比较自己的实验结果和电脑软件大数据实验结果,你有什么发现?

策略1
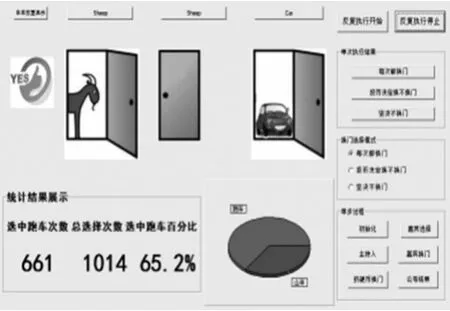
策略2
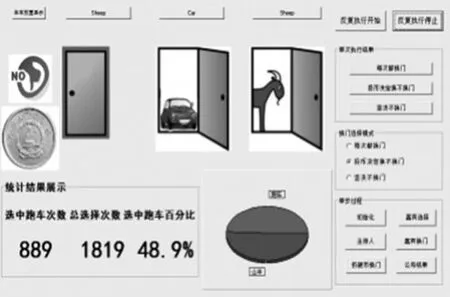
策略3
3.借力合情推理,理解本质。
师:那么,为什么不换门的可能性是三分之一呢?
生:因为不换门中有三扇门可以选一扇,猜中的就只有一扇门,所以就是三分之一。
师:为什么换门的可能性是三分之二呢?
生:就是换门和不换门是互补的,一个是三分之一另一个就是三分之二。
生:第一种可能是羊、羊、车,二号门的可能是羊、车、羊,三号门可能是车、羊、羊。好,我们来看,如果第一次选中的是羊,主持人打开羊,我们选择的就是车。第二次选择的是车,主持人打开的是羊,我们换门选择的也是羊。第三次我们选择的羊,主持人打开的也是羊,我们换门就是车。这三种情况赢得汽车的概率就是三分之二。
【环节点评】
学生通过动手实验,样本数据分析和合情推理层层展开,步步深入,学生经历了猜想、实验、验证和推理的探究过程,从中挖掘“三门问题”所蕴含的奥秘,从而进一步建立“三门问题”的数学模型。从第一次对比最初猜测和我们的实验数据,学生惊奇地发现:三种策略的统计结果跟最初的猜想有较大的偏差,学生猜测换门和投硬币的概率都是二分之一,但实验数据比我们的猜测要高;第二次对比我们的实验数据和大数据实验数据,让学生感受到统计建模与一般的数学建模有所不同,它充满了很强的不确定性,我们需要尽力降低这种不确定性,尽量对这种不确定性进行量化。从而进一步启发学生,感性经验和猜想有时并不是很准确,猜想还需借助实验数据进一步验证,如果不动手实验,思维将会受到阻碍或发生错误,数学实验相当于给学生搭建了一副理解数学本质的“脚手架”。
四、教学反思
上数学实验课的目的是让学生在实验操作中不断积累“做的经验”“想的经验”,在此过程中体验数学、感悟数学,完成数学化的学习过程,触摸数学本质。上好一节数学实验课还要注意以下几点。
(一)素材选择需有度
“三门问题”是一个富有挑战性、有一定难度的数学问题,往往会给人们造成理解上的困惑,更何况是小学生。我们相信,只要找到一个合适的途径和方法,一些高等数学知识也可以让小学生进行理解。考虑到六年级学生有一定的概率知识储备,借助数学实验和合情推理,可以促进学生理解“三门问题”的解题策略。不过,我们也注意到一个现象,有部分学生虽然完成了教学流程,对学习材料也保持着浓厚的兴趣,但对和自我最初猜想差异较大的正确结果还会有一个理解的过程,我们要允许学生有自我调整的学习过程。
(二)学生猜想有引导
当学生出现猜想时,不能因为学生说不清缘由而指责学生“瞎猜”或“胡说八道”,而应该及时鼓励,适时表扬,容忍学生出现短暂的“忘乎所以”,久而久之,学生就不会有所顾虑,遇到新问题时便敢于猜想。在鼓励学生大胆猜想的同时,适时引导学生对其思路进行矫正,如果教师发现学生的猜想完全偏离轨道,可以适当追问或提供一些小建议,引导学生调整思路,重新分析,久而久之,学生猜想的方法越来越合理化,真正让猜想为学习所用,让猜想为课堂所用,猜想才更具有意义。
(三)实验组织重有效
在做实验前,如果“三门问题”游戏规则要求不明确、不到位,代替三扇门的三个杯子形状、颜色不一,实验者的心态,这些都会增加学生实验的难度,使得实验数据不够稳定,使一些学习水平和理解能力不足的学生产生困难,对大数据实验结果产生怀疑,白白浪费了宝贵的学习时间。又比如,有一些学生选择投币实验,可以提醒学生把硬币放入纸杯,杯口用掌心盖住摇动,可以让实验数据更准确。所以,教师在设计活动要求时应简要、明确,提供充分的实验时间,关注学生的实验进度、探究互动和辨析明理的过程。
(四)数学思考要充分
毋庸置疑,“三门问题”是集趣味和难度(与直觉相悖)于一体的,没有一定的思考和实验时间,只能沦为机械操作,无法获得实质性的思维提升。对游戏的理解也好,对实验规则的设计也好,还是实验过程,都应让学生手脑并用,注重培养学生边观察、边想象、边思考的习惯。可以采用“先做后想”或“先想后做”等方式,将观察与操作、想象与操作、想象与思考等结合起来,提高实验活动的质量。
课即将结束,学生还沉浸在“三门问题”的思考中,猜测如果是四扇门、五扇门或更多的门,同样的游戏规则,结果又会是怎样的呢?提出问题的学生还不断提出解决问题的新规则和方法。教师让学生给这节课取个题目,学生纷纷抛出:车羊问题、赢车问题、三门问题、三门风波等。正如一位学生所说的,从最初的猜想可能性是二分之一,到实验所得三个不同的数据,虽然知道了结论,但这个结论和猜想相差较大,心理好比过山车一样,经历了一场“三门风波”。可见,从研究三扇门的获奖概率问题,到研究四扇门、五扇门甚至更多的门的获奖概率问题,对学生而言,他们经历的是学习之旅,思维之旅,精神升华之旅。这就是数学实验课的魅力所在!

