高轨SAR非平直几何动目标成像影响建模
, , ,
( 1.中国科学院空间信息处理与应用系统技术重点实验室, 北京 100190; 2.中国科学院电子学研究所, 北京 100190; 3.中国科学院大学, 北京 100049; 4.中国国际工程咨询公司, 北京 100048)
0 引言
地球同步轨道SAR(高轨SAR)轨道高度高,具有覆盖范围广、轨道回归周期短、可定点连续观测等特点,在动目标探测方面具有很大的优势[1-2]。机载/低轨SAR中,一般在平直成像几何下开展目标运动影响分析。而高轨SAR轨道高度大幅提升,斜视成像过程中星地几何关系剧烈变化且呈现非平直特点,动目标对成像的影响程度和方式发生变化。因此,需要建立高轨SAR非平直斜视几何下的动目标成像影响模型,为高轨SAR动目标参数估计和精细处理奠定理论基础。
1971年,Raney首次进行了SAR动目标检测的研究,指出低速运动目标径向速度引起方位位置偏移,径向加速度和方位向速度引起散焦[3]。Sharma等指出,目标方位向加速度和径向二次加速度会造成三次相位误差,引起SAR图像方位向的非对称畸变[4]。文献[5]指出了机载正侧视下目标速度、加速度对方位向位置产生的影响,并给出目标运动引起的方位展宽量的解析表达式。文献[6]给出了机载SAR斜视模型下目标位置偏移量和展宽量的表达式。Sabry建立了斜视情况下瞬态距离多普勒历程模型,分析了目标运动在距离向和方位向上的影响[7]。与机载/低轨SAR相比,高轨SAR不仅包含斜视成像,并且星地相对速度不再与地面平行(即非平直几何),以上研究构建的平直成像几何条件无法直接适用于高轨SAR,因此有必要针对高轨SAR非平直大斜视成像特点,建立动目标成像影响模型并进行分析。
本文简单回顾了平直成像几何下动目标成像影响模型。建立大地坐标系下高轨SAR非平直大斜视成像几何,基于等距离-多普勒方程推导出高轨SAR动目标成像位置偏移、二次相位误差和三次相位误差的解析表达式,与SAR平直成像几何下的成像影响进行了对比分析。仿真验证了高轨SAR非平直斜视成像几何下动目标成像影响模型的正确性和精确性。
1 SAR平直成像几何动目标影响模型
采用SAR平行于地面斜视成像的几何模型,图1为机载SAR与动目标P的几何关系示意图,以动目标为原点建立坐标系。载机位置矢量为rsxs,ys,zs,其速度矢量为Vsvs,x,0,0,动目标P位置矢量为rPxt,yt,zt,方位时间η=0时,其坐标为0,0,0,速度矢量为Vtvx,vy,0,目标P到载机S的斜距矢量为rso。
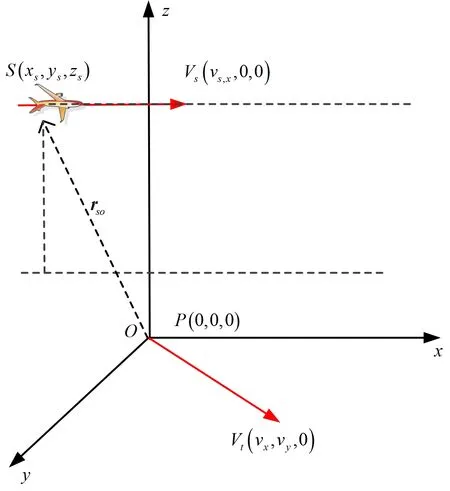
图1 机载SAR平直成像几何图
目标运动将会在回波信号中引入新的多普勒参数分量,若在成像过程中采用静止目标的多普勒参数对动目标进行方位向压缩,则会由于失配导致动目标在SAR图像上出现方位位置偏移、散焦等现象。目标的方位位置与多普勒中心频率相关,运动产生的多普勒中心频率误差会使目标在方位位置上发生偏移。根据文献[6],结合本文采用三维空间坐标的表示形式,推导得到动目标位置偏移量为

由式(1)可知,动目标的方位位置偏移量与目标位置、速度相关。当正侧视情况,即xs=0时,其方位偏移量为ysvy/vs,x,此时vy即为动目标的径向速度,表明动目标的径向速度引起方位位置偏移。
此外,多普勒调频率影响SAR图像的聚焦效果。调频率误差会导致动目标方位向的散焦,其引起的二次相位误差在通带边缘达到最大值。推导得到二次相位误差为
式中,Ts为合成孔径时间。实际情况中,目标速度远小于载机速度,所以主要由方位向速度引起二次相位误差。
机载SAR飞行速度与地面基本平行。低轨SAR采用二维偏航导引技术,星地相对运动速度基本平行于成像区域地平面进行正侧视成像。在平直正侧视成像几何下,动目标速度可以分解为与飞行速度平行的方位向速度和与飞行速度垂直的径向速度。基于上述传统影响模型可以得到以下结论:正侧视情况,径向速度只引起偏移,方位向速度只引起散焦,两个速度的影响相互独立;斜视情况,径向速度和方位向速度同时引起偏移,只有方位向速度引起散焦;无论是正侧视还是斜视情况,动目标成像在方位位置发生偏移。
2 SAR非平直斜视成像几何动目标影响模型
高轨SAR在长时间连续观测下采用大斜视成像,受到地表曲率和地球自转影响,星地相对运动速度与成像地平面不再平行,表现出垂直于地平面俯仰方向速度分量。下面根据高轨SAR非平直斜视成像特点,在大地坐标系下建立等效成像几何,构建适用性更好的动目标成像影响模型,讨论该模型与现有平直成像几何影响模型的关系,分析径向速度方向的偏移、俯仰方向速度分量造成的偏移和散焦等。
2.1 高轨SAR非平直斜视成像几何建模
图2为大地坐标系下,高轨SAR非平直斜视成像几何。t=0时刻动目标P位于大地坐标系原点O,x轴指向地平面正东方向,y轴指向正北方向,z轴满足右手螺旋法则,目标运动速度矢量Vt。卫星位置矢量rso,投影到x-y平面的矢量为rso,xy,投影到z轴的矢量为rso,z。在成像时间内(几十秒),卫星运动近似为匀速直线运动,速度矢量为Vs,投影到x-y平面的矢量为Vs,xy,投影到z轴的矢量为Vs,z(卫星俯仰速度分量)。
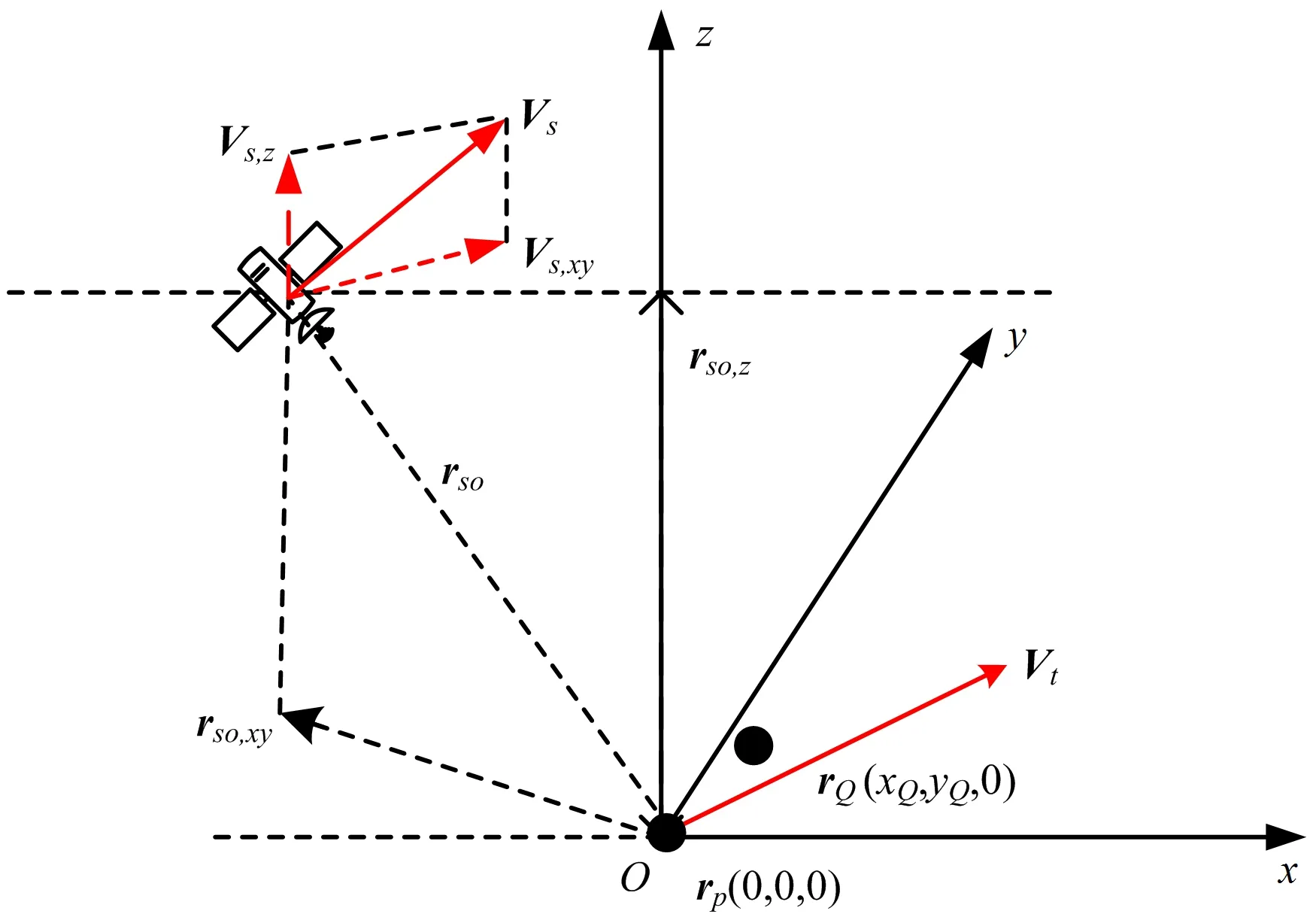
图2 大地坐标系下高轨SAR成像几何图
SAR成像过程本质上是回波信号与匹配滤波器的互相关过程,动目标成像就是动目标回波信号与静止目标匹配滤波器的互相关过程。假设某一静止目标Q,零时刻其斜距和多普勒频率与动目标P的斜距和多普勒频率相等,则静止目标位置矢量rQ即为动目标的成像位置偏移,动目标P与静止目标Q多普勒调频率和更高阶多普勒调频率的差异反映成像散焦。
2.2 动目标成像位置偏移模型
已知方位中心时刻,动目标P实际位于大地坐标系的原点,设某静止目标Q的坐标为rQ=xQ,yQ,0。P和Q与卫星间的距离历程分别表示为
RPη=rso+Vs·η-Vt·η
(3)
RQη=rso+Vs·η-rQ
(4)
建立方位中心时刻动目标P与静止目标Q的等距离等多普勒方程:
联立式(3)、式(4)、式(5),可得
在x-y平面内,得到
将rso,xy-rQ和rso,xy分别投影到Vs,xy方向和Vs,xy垂直方向上,进而得到rQ在两个正交矢量上的投影,Vs,xy方向和Vs,xy垂直方向单位矢量分别为
rso,xy在Vs,xy方向和Vs,xy垂直方向上的投影大小分别为
由式(7)第二个等式可得,rso,xy-rQ在Vs,xy方向上的投影大小为
由式(7)第一个等式可得,rso,xy-rQ在Vs,xy垂直方向上的投影大小为
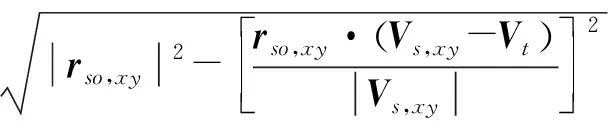
(13)
式中,正负号代表投影为正向或者相反的方向。
相应地,rQ在Vs,xy方向和Vs,xy垂直方向上的投影大小分别为
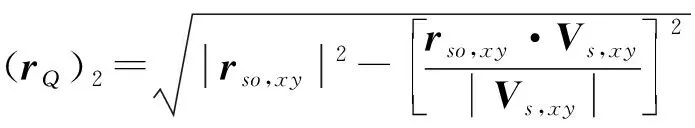
根据上式可以计算出两个静止目标Q,其中偏移量小于幅宽的为有效值。
根据非平直斜视模型下目标运动引起的位置偏移表达式(式(14)、式(15)),高轨SAR卫星俯仰速度分量Vs,z对位置偏移没有影响。目标在平行和垂直卫星地面速度方向都会发生位置偏移,平行方向上的偏移表达式(式(14))与平直正侧视情况下的偏移相同,垂直方向上的偏移(式(15))并不严格等于零。当Vt⊥rso,xy时,两个方向偏移同时等于零。当Vt‖rso,xy时,两个方向偏移同时达到最大。
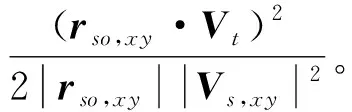
对于高轨SAR非平直斜视模型,垂直卫星地面速度Vs,xy方向上的偏移分量无法忽略,因此本文构建的精确位置偏移模型对于分析高轨SAR动目标成像偏移是非常必要的。
2.3 动目标相位误差模型
由于高轨SAR合成孔径时间长于低轨SAR,其信号精确建模和成像处理除了需要依赖多普勒中心频率和调频率外,还需要利用更高阶多普勒调频率。根据等距离等多普勒关系,动目标P成像位置偏移至静止目标Q,此时P点与Q点多普勒调频率和更高阶多普勒调频率的差异,反映了P点散焦情况。
计算式(3)和式(4)的二阶导数,得到动目标P和静止目标Q的多普勒调频率分别为
利用等距离等多普勒方程,得到多普勒调频率差异为
Δfr=fr,P-fr,Q=
多普勒调频率引起二次相位误差:
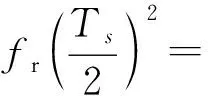
类似地,计算式(3)和式(4)的三阶导数,得到动目标P和静止目标Q的多普勒二阶调频率分别为
利用等距离等多普勒方程,多普勒二阶调频率差异为
Δf2r=f2r,P-f2r,Q=
多普勒二阶调频率引起三次相位误差:
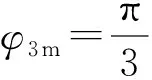
(23)
根据非平直斜视模型下目标运动引起的相位误差表达式(式(19)、式(23)),高轨SAR卫星俯仰方向速度对二次相位误差没有贡献,但对三次相位误差有贡献。当卫星俯仰方向速度为零时,本文建立的二次相位误差表达式与现有文献一致,本文建立的相位误差表达式是现有文献的扩展。
假设目标运动速度大小不变、方向可变,Vs,xy-Vt=Vs,xy时,二次和三次相位误差同时等于零。当Vt‖Vs,xy时,二次相位误差达到最大。
3 仿真试验与分析
为了验证上述动目标成像影响的推导和分析,下面对高轨SAR进行仿真试验,首先进行高轨SAR成像性能的分析及仿真参数的设置,然后由仿真结果定量和定性分析目标运动对成像偏移和散焦产生的影响。
3.1 参数设计分析
本文主要考虑高轨SAR海面动目标探测的问题。因此选用C波段雷达、60°倾角圆形轨道进行仿真,以缩短成像所需合成孔径时间,提高海面动目标探测的可实现性;名义分辨率选择100 m,以减小去相干等因素对高轨SAR相干成像的影响。表1给出卫星轨道参数和雷达参数。设计可成像条件包括:地面入射角10.6°~66.4°,地面斜视角0°~60°,地距平面二维分辨夹角30°~90°,在上述参数下仿真得到高轨SAR一个轨道回归周期内(约24 h)全球可成像时长如图3所示。仿真结果表明,我国周边海域可成像时长普遍超过12 h,形成了对海面动目标进行长时间探测的条件。
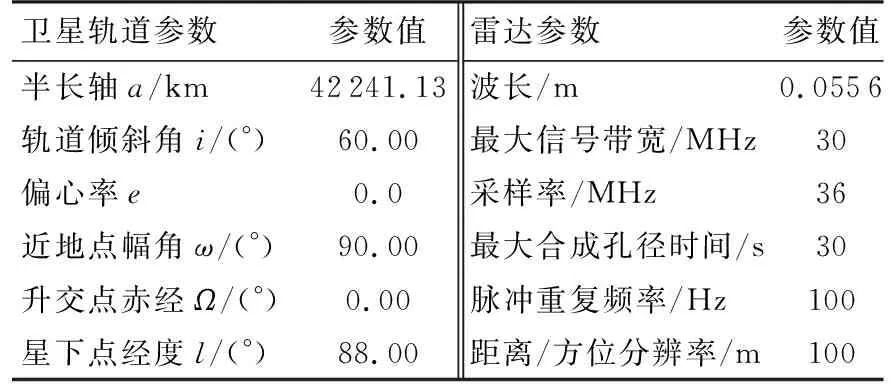
表1 卫星轨道与仿真参数
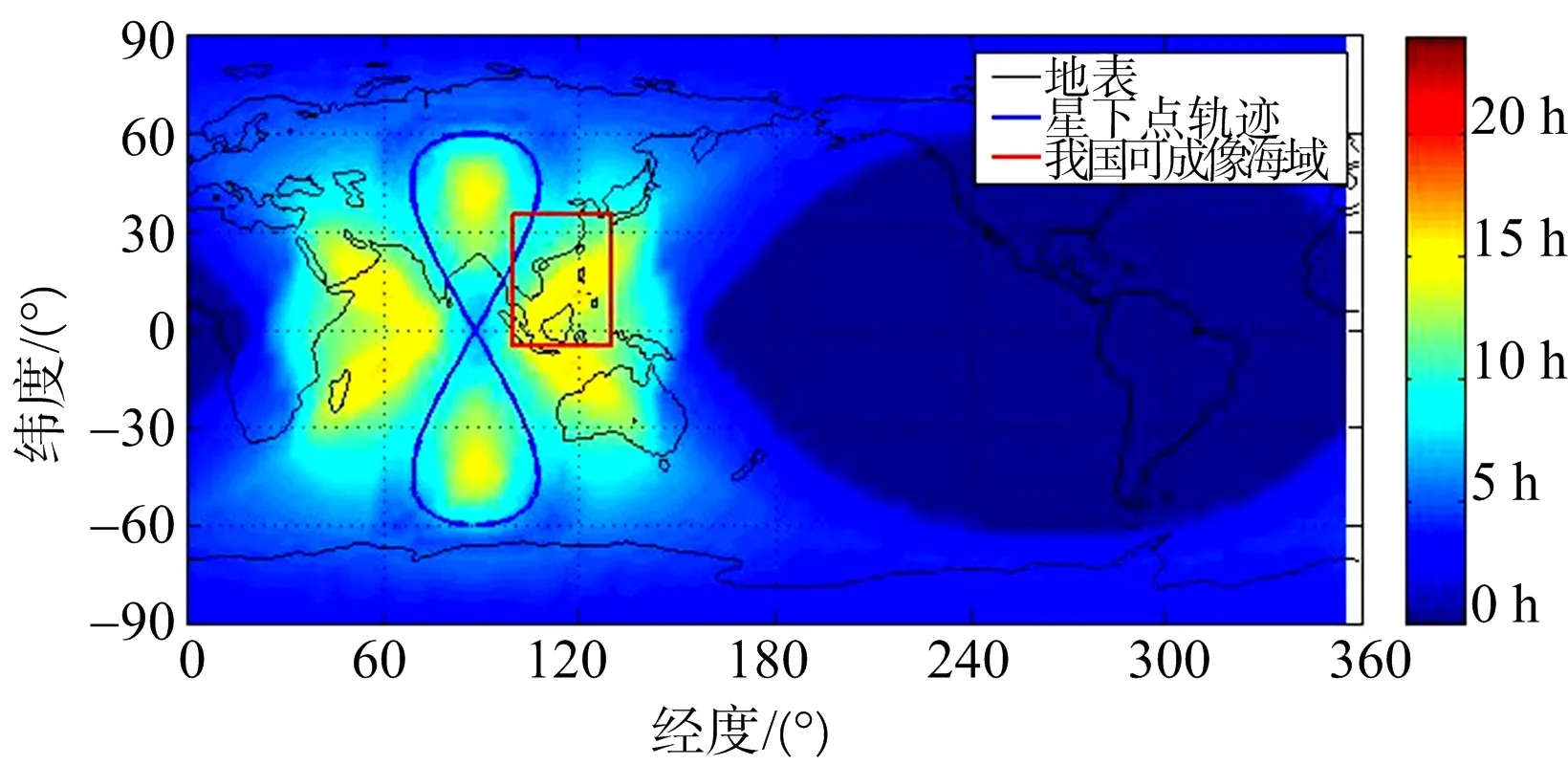
图3 高轨SAR全球可成像时间图
设置一个典型目标,经度为100°、纬度为0°。图4为一个轨道周期内该目标可成像弧段对应的星下点轨迹,图5为目标地面斜视角变化情况。
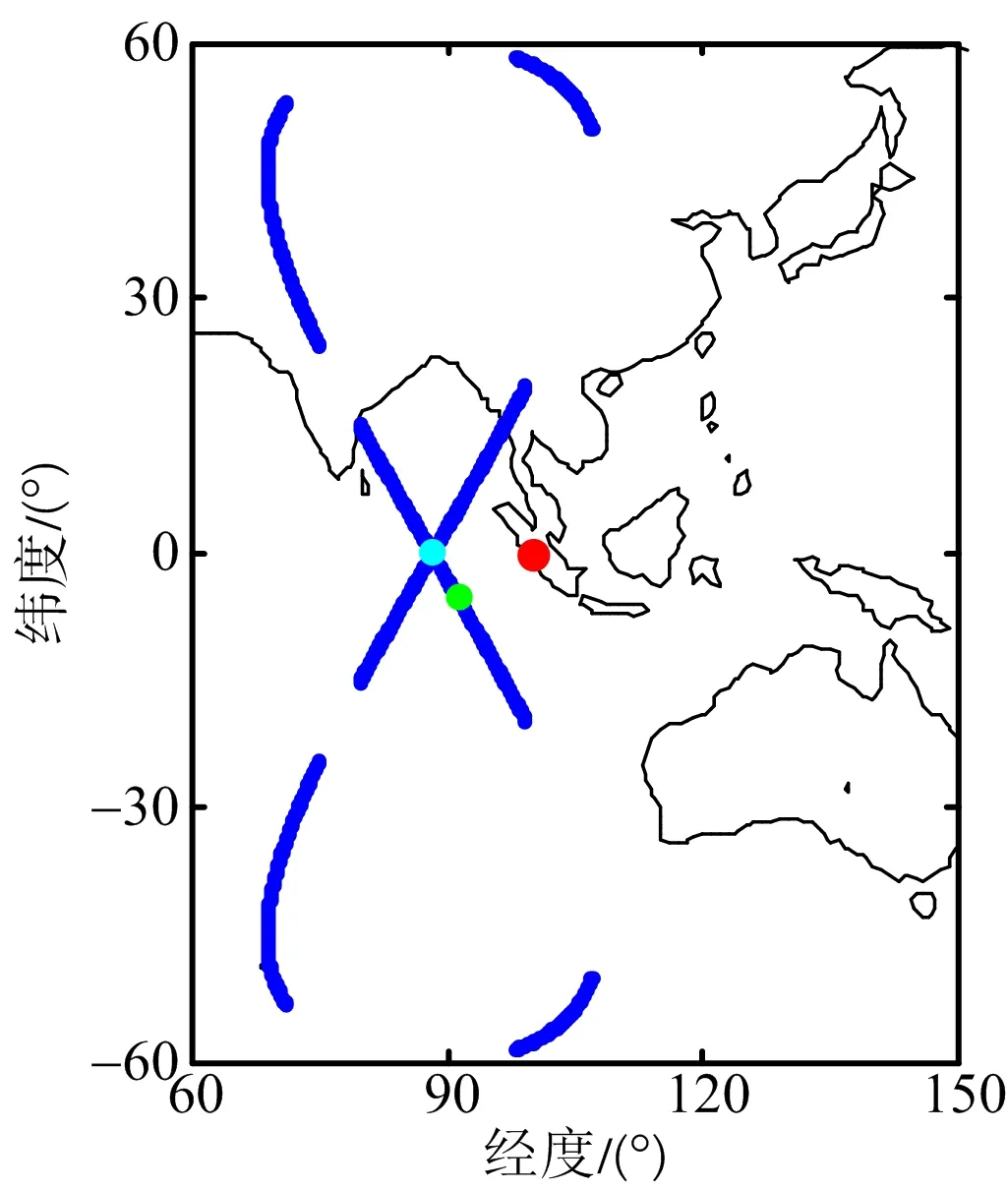
图4 目标可成像弧段
选择正侧视成像(卫星真近心角-96°)和大斜视成像(卫星真近心角-90°),并按照名义分辨率100 m对雷达参数进行更新,得到两个成像几何下的雷达参数和系统性能参数如表2所示。
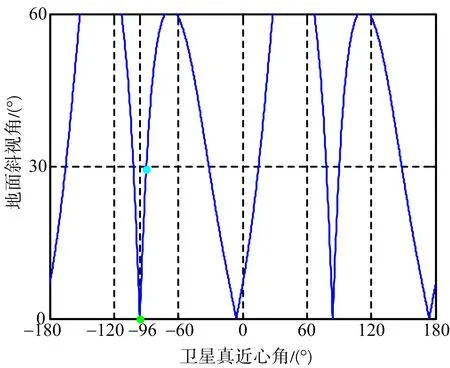
图5 目标地面斜视角变化
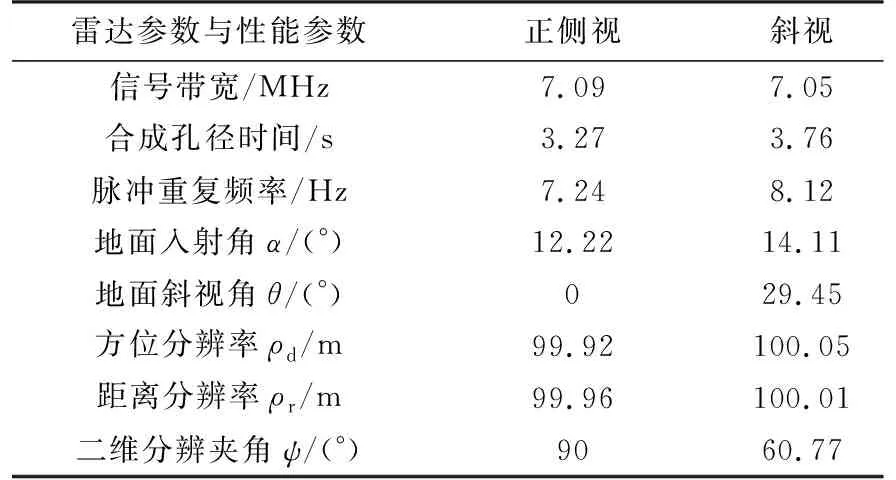
雷达参数与性能参数正侧视斜视信号带宽/MHz7.097.05合成孔径时间/s3.273.76脉冲重复频率/Hz7.248.12地面入射角α/(°)12.2214.11地面斜视角θ/(°)029.45方位分辨率ρd/m99.92100.05距离分辨率ρr/m99.96100.01二维分辨夹角ψ/(°)9060.77
3.2 成像偏移仿真分析
本节仿真分析高轨SAR动目标成像偏移。采用3.1节分析得到的雷达与轨道参数,采用BP算法在地距平面对目标成像。由于在大片海域中船只的常规航速为7~15 m/s(15~30节),因此本文对目标设置15 m/s的速度大小。
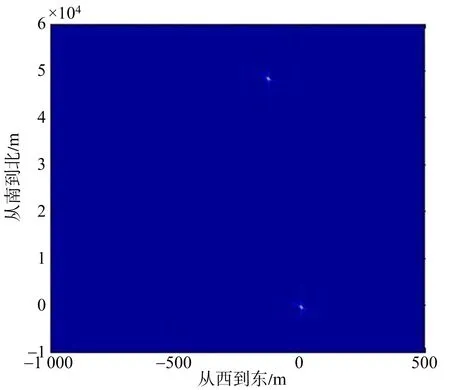
图6 斜视向东15 m/s运动目标与静止目标成像
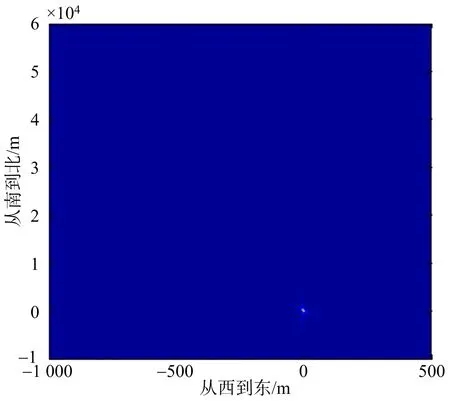
图7 斜视向北15 m/s运动目标成像
首先仿真向正东和正北运动目标的成像偏移。图6为斜视情况下正东运动的目标与静止目标成像结果对比图;图7为斜视情况下正北运动的目标与静止目标成像结果对比图。计算得到正东运动成像偏移大小为49 939 m,正北运动成像偏移大小为0.007 m。同样仿真得到正侧视情况下,正东运动和正北运动目标的成像偏移大小分别为32 208 m,18 698 m。
成像偏移的理论计算公式(式(14)、式(15))中相关参数的计算结果如表3所示。
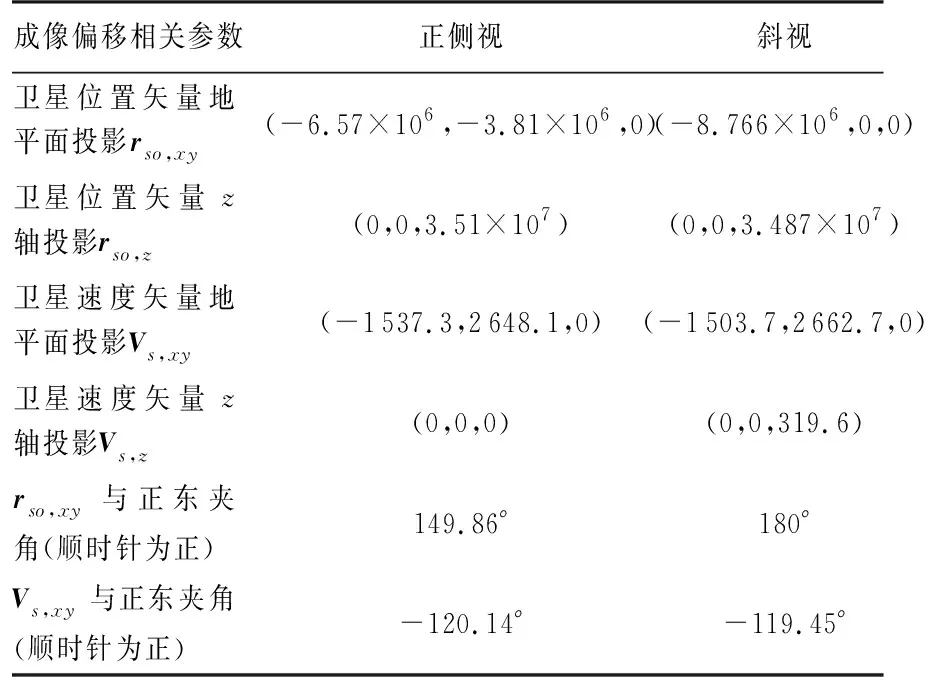
表3 成像偏移相关参数计算值
据此计算得到正侧视和斜视情况下,动目标的成像偏移理论计算结果如表4所示。在正侧视、斜视情况下理论结果与仿真结果基本一致。垂直卫星速度方向上的偏移并不严格等于零。对于斜视情况,正东运动的目标垂直卫星速度方向上的偏移分量达到24 070.47 m,与卫星速度方向上的偏移量级一致,无法忽略,说明本文构建的精确偏移模型对于分析高轨SAR动目标成像偏移是非常必要的。
为进一步分析目标速度方向和与卫星相对位置关系对成像偏移产生的影响,本文对正侧视和斜视两种情况,仿真15 m/s运动目标成像偏移与运动速度方向的关系。
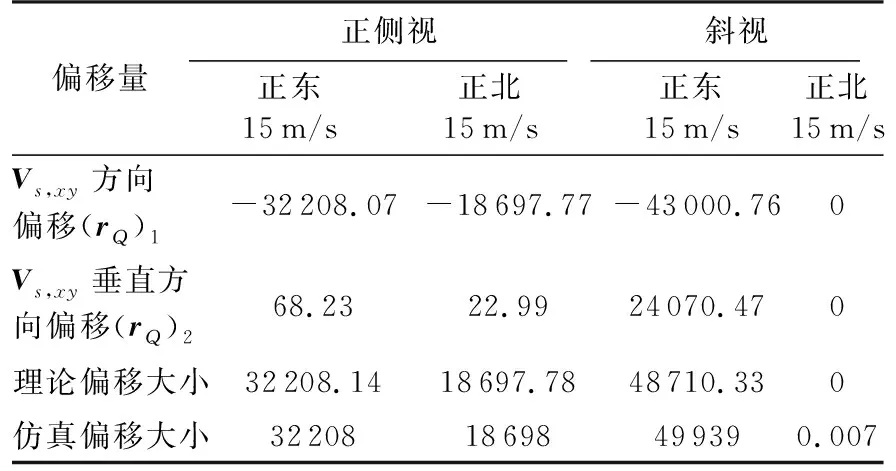
表4 成像偏移理论计算结果与仿真结果
图8~图10表示正侧视成像下,动目标在卫星速度方向、卫星速度垂直方向的偏移,以及合成偏移大小随运动方向变化的情况。当目标速度Vt与卫星位置矢量地面投影rso,xy夹角为90°,270°,即Vt⊥rso,xy时,在卫星速度及垂直方向的成像偏移同时为零;当Vt与rso,xy夹角为0°,180°,即Vt‖rso,xy时,两个方向偏移大小同时最大。在卫星速度方向的偏移比卫星速度垂直方向偏移大3个数量级,一般可以忽略,这与低轨平直几何成像影响模型下的结论一致。
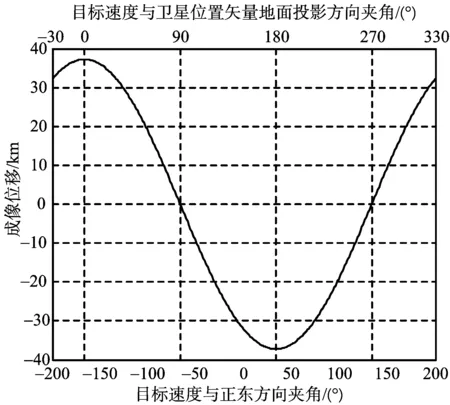
图8 正侧视卫星速度方向的位置偏移
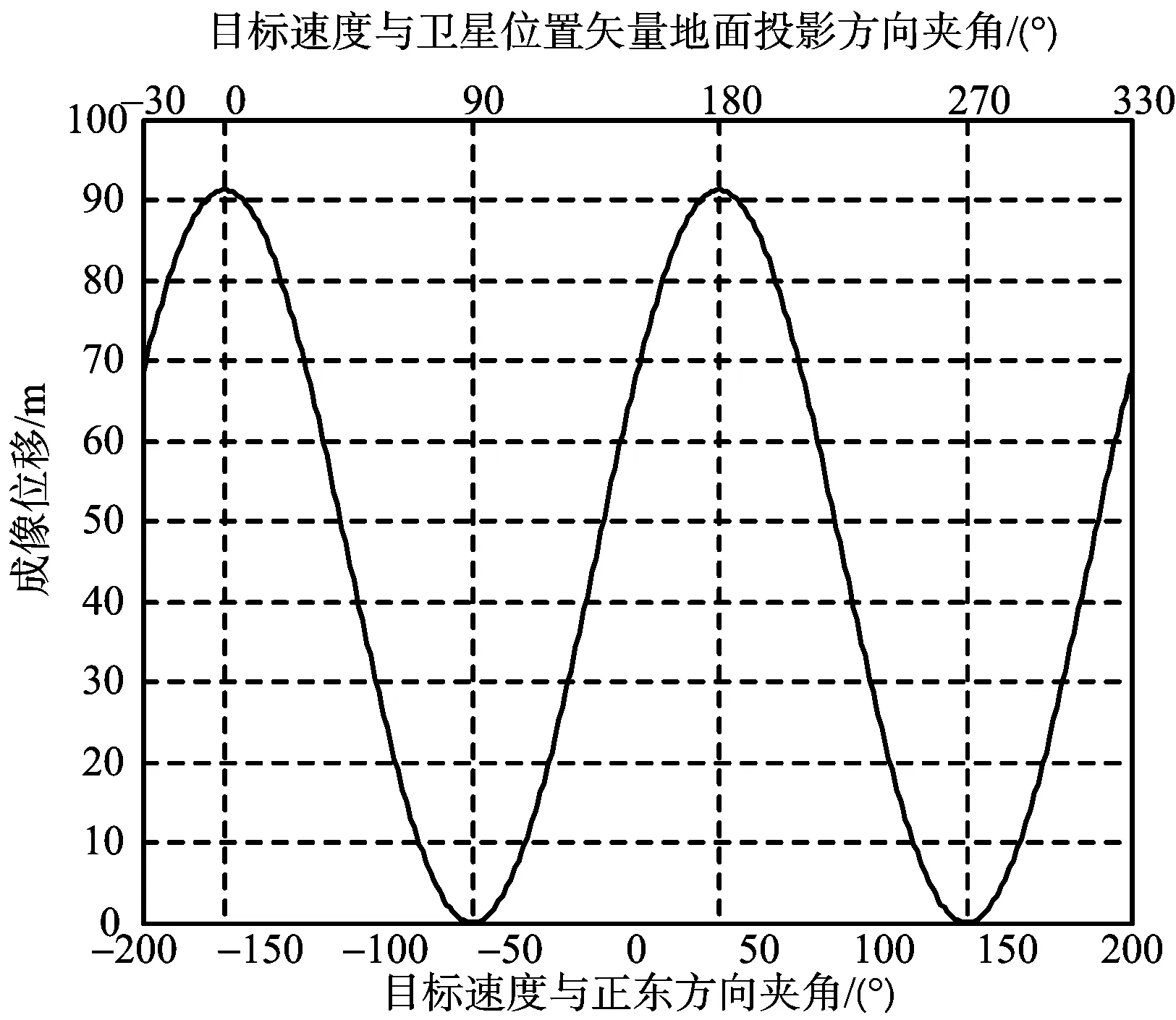
图9 正侧视卫星速度垂直方向的位置偏移
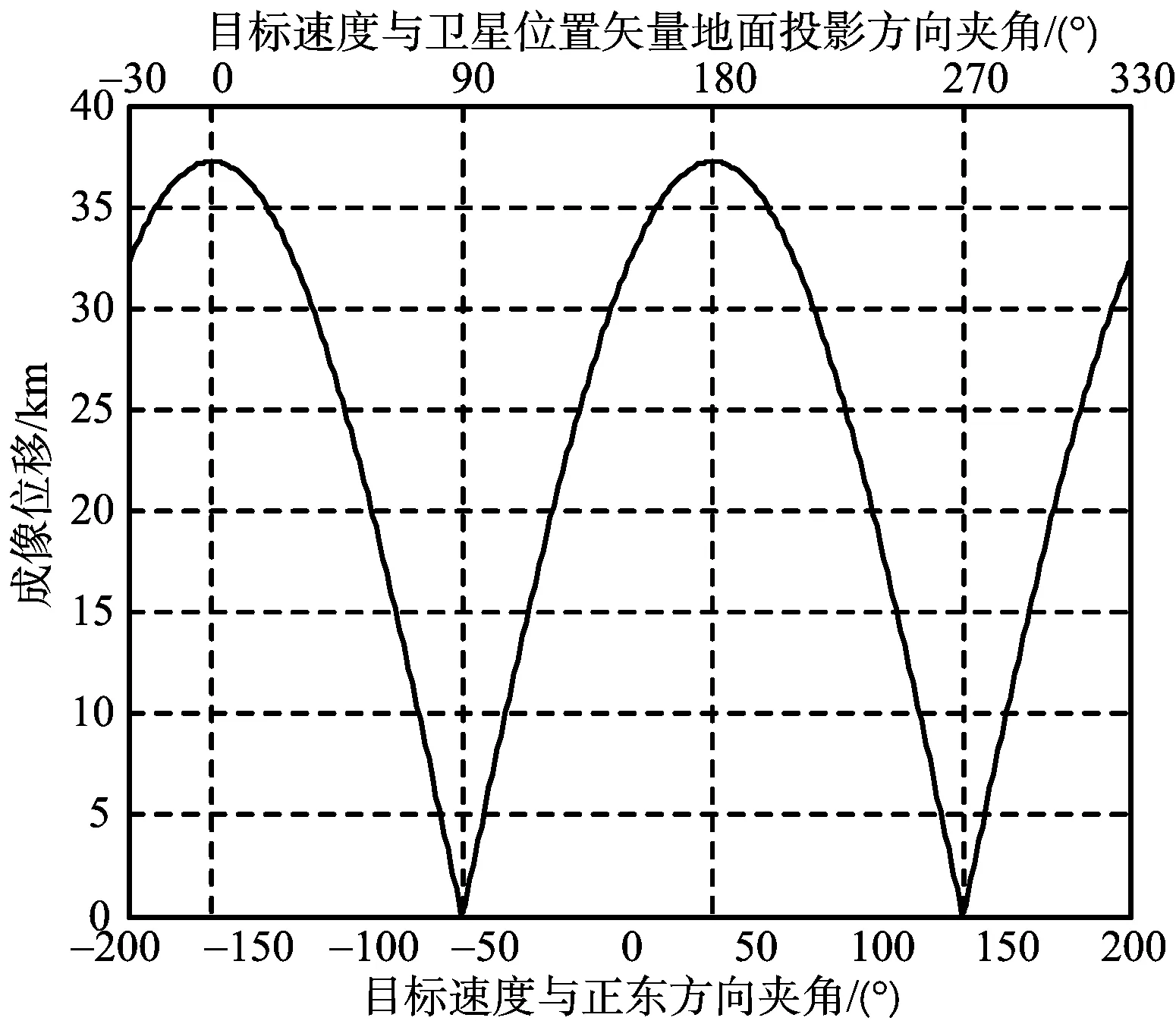
图10 正侧视位置偏移大小
图11~图13表示斜视成像下的偏移情况,同样当Vt⊥rso,xy时,两个方向偏移同时等于零,当Vt‖rso,xy时,两个方向偏移同时达到最大。动目标在卫星速度方向和垂直方向产生数量级相当的成像偏移,垂直卫星速度方向上的偏移分量无法忽略。
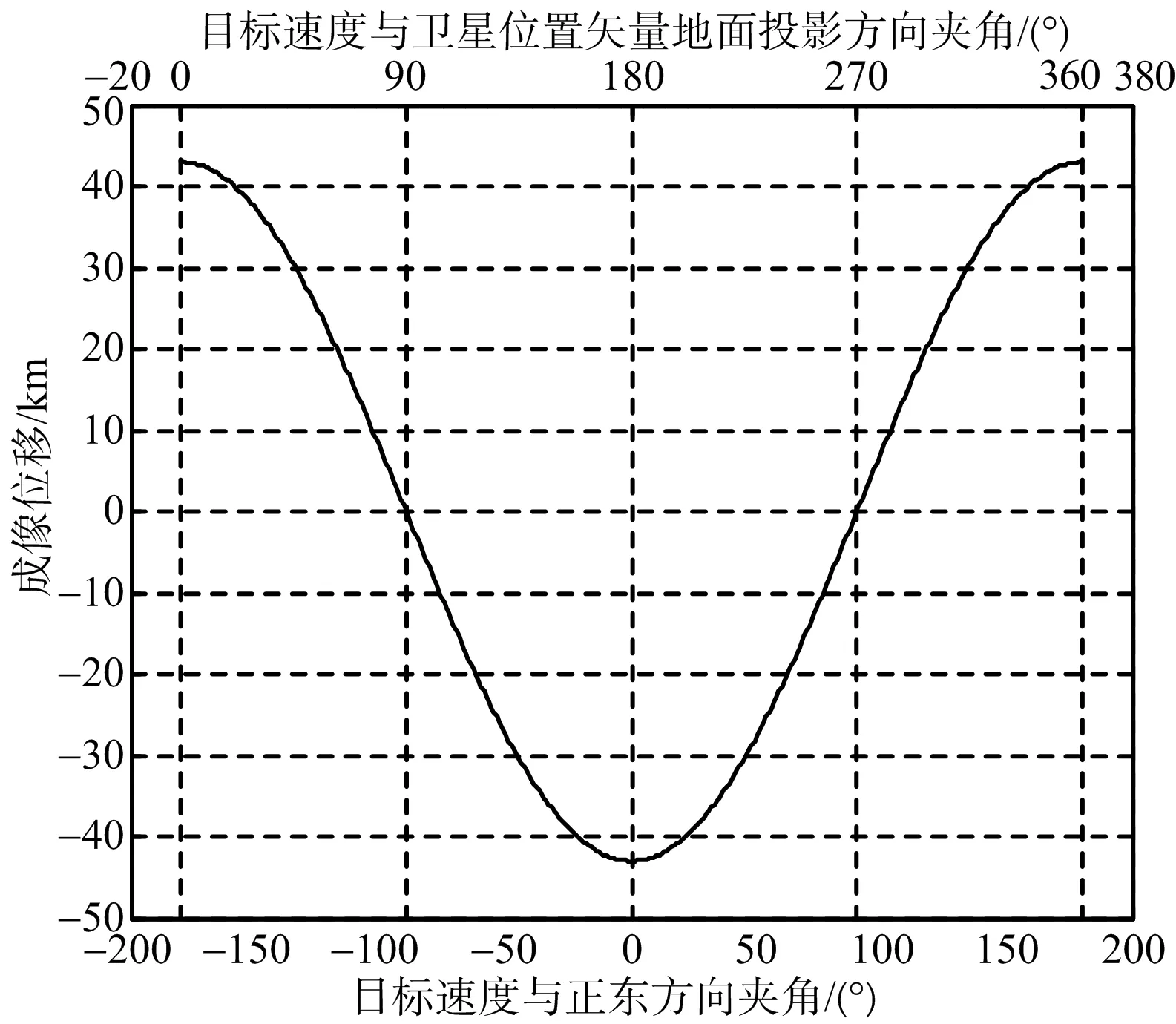
图11 斜视卫星速度方向的位置偏移
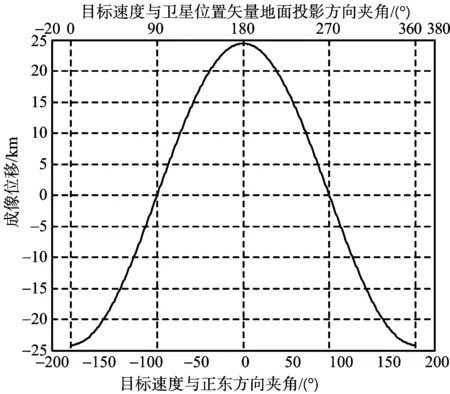
图12 斜视卫星速度垂直方向的位置偏移
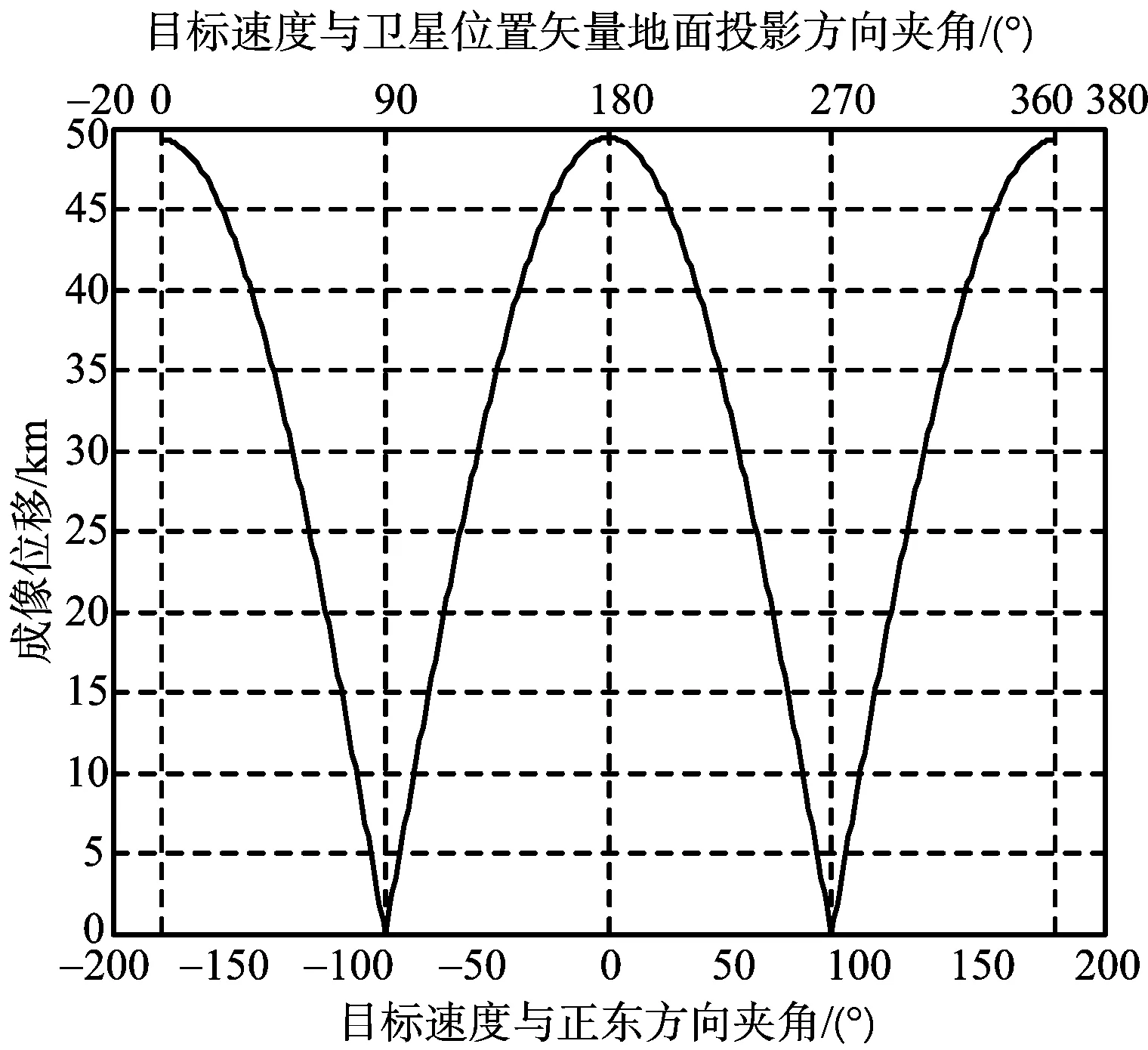
图13 斜视位置偏移大小
3.3 相位误差仿真分析
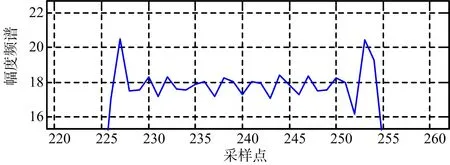
图14 向东运动时目标幅度频谱
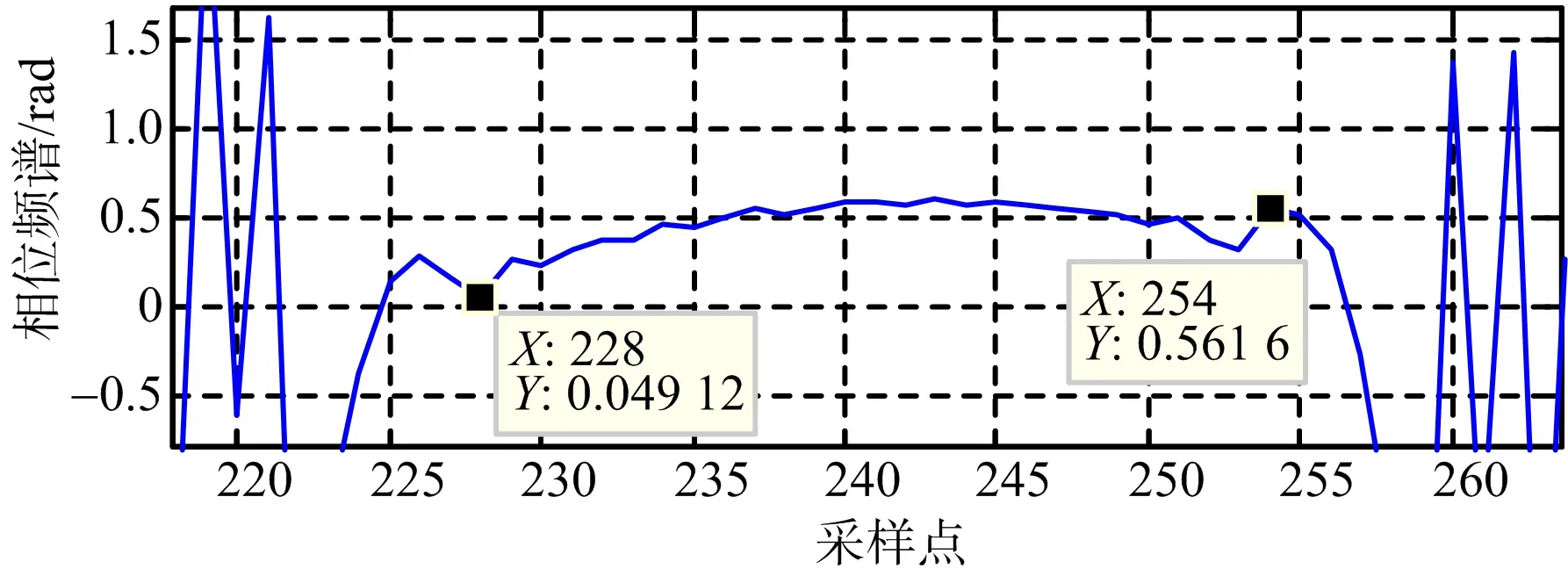
图15 向东运动目标相位频谱
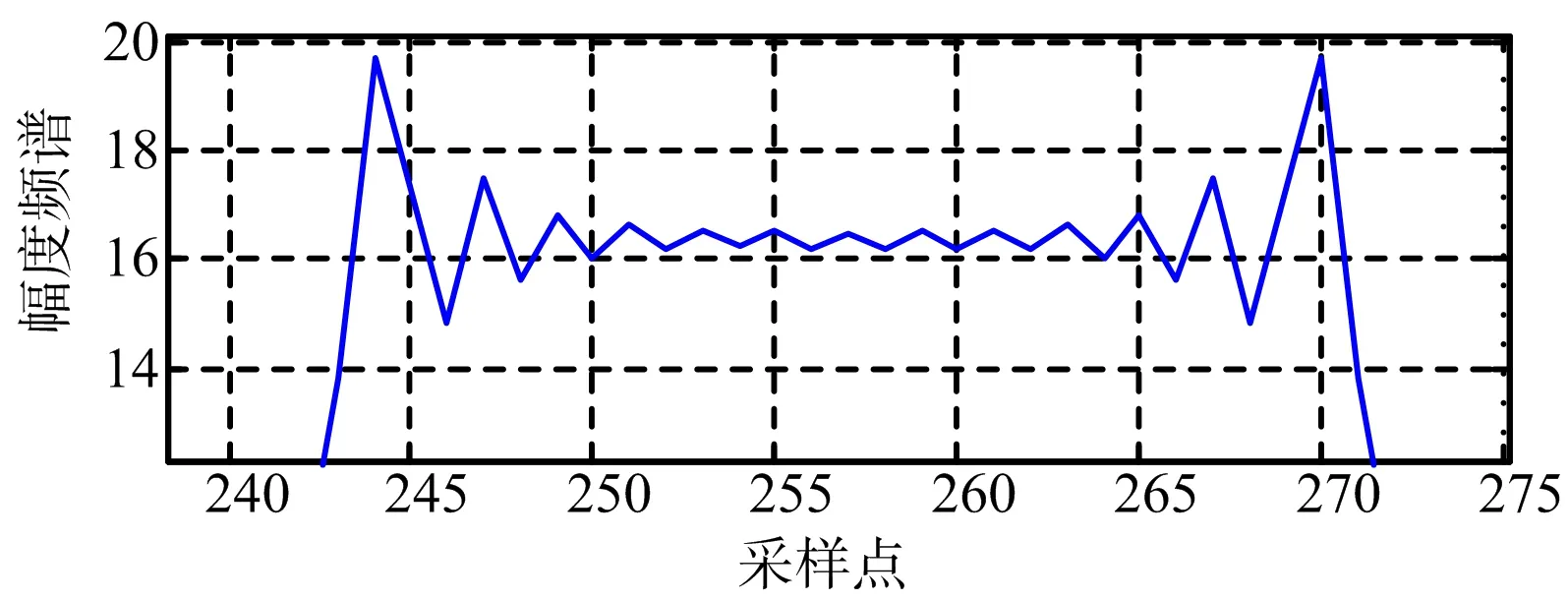
图16 向北运动时目标幅度频谱
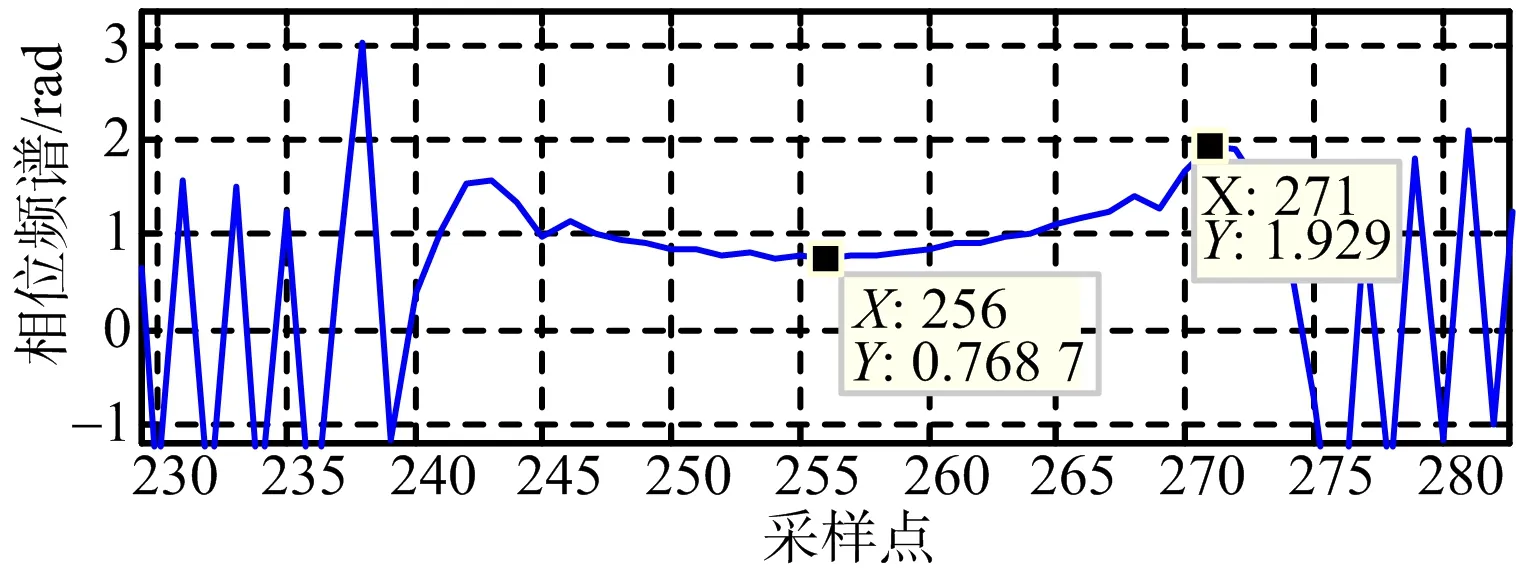
图17 向北运动时目标相位频谱
本节仿真动目标相位误差,参数设置与前文一致。斜视情况下,两个成像动目标的幅度频谱和相位频谱如图14~图17所示,计算得到向东运动目标的二次相位误差为29.36°,向北运动目标的二次相位误差为66.48°。根据相位误差计算公式(式(19)),得到正东方向和正北方向运动目标的二次相位误差理论值分别为28.43°和50.45°。仿真与理论结果基本一致。

图18 正侧视二次相位误差
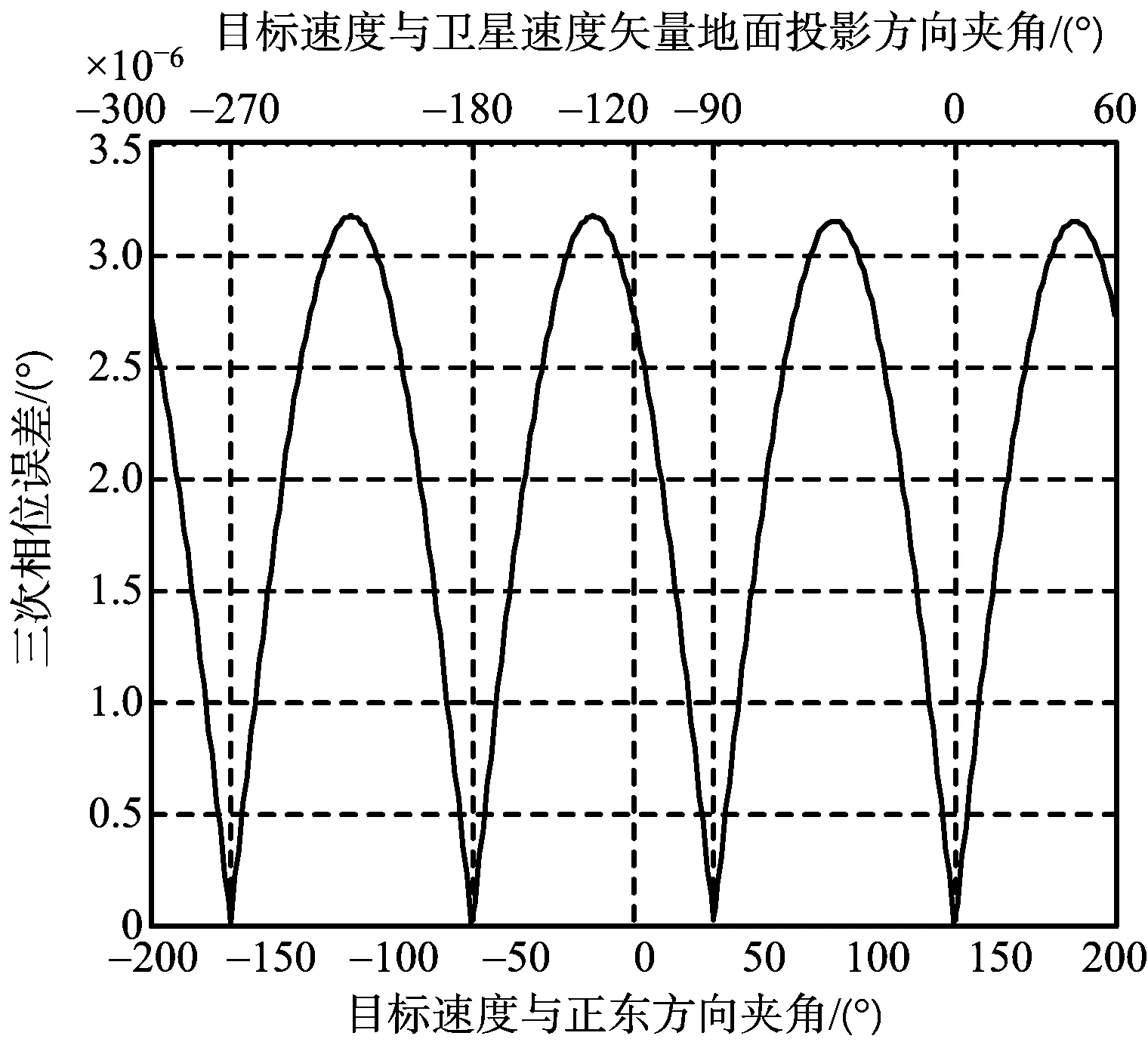
图19 正侧视三次相位误差
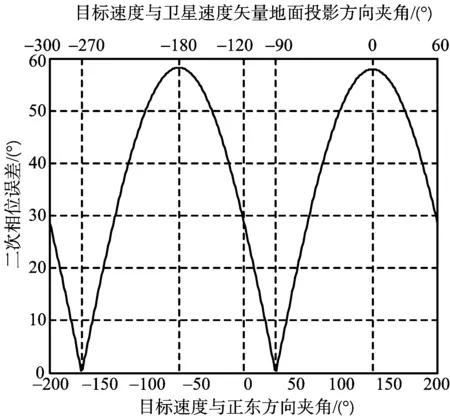
图20 斜视二次相位误差
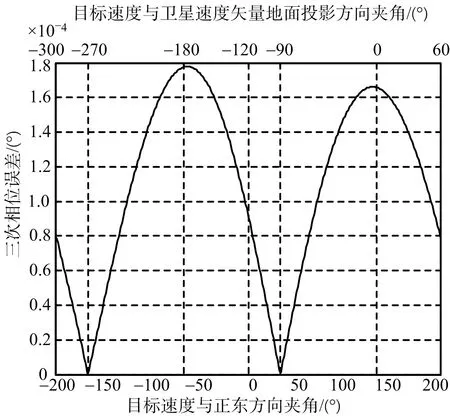
图21 斜视三次相位误差
下面仿真正侧视和斜视情况下,目标运动速度方向和卫星速度方向对相位误差的影响。由图18~图21可知,正侧视和斜视情况下,当目标速度Vt与卫星速度地面投影Vs,xy夹角为-90°, -270°,即Vt⊥Vs,xy时,二次和三次相位误差同时等于零;正侧视情况下,当Vt与Vs,xy夹角为0°, -180°,即Vt‖Vs,xy时,二次相位误差达到最大;斜视情况下,当Vt‖Vs,xy时,二次和三次相位误差同时达到最大。三次相位误差十分小,一般可忽略。
4 结束语
本文对高轨SAR动目标成像影响进行了研究,针对高轨SAR非平直大斜视成像特点构建了动目标成像影响模型,推导得到动目标成像位置偏移、二次相位误差和三次相位误差的解析表达式,并从高轨SAR动目标探测的角度对雷达参数和卫星轨道进行分析论证。本文构建的高轨SAR动目标成像影响模型是传统低轨/机载SAR的推广,并且能更加精确地分析非平直大斜视情况,为高轨SAR动目标成像影响定量化分析提供了理论模型,为高轨SAR动目标参数估计及重定位、再聚焦处理提供了指导。

