基于改进RFT算法的宽带LFMCW雷达运动补偿方法
, , ,
( 1.空军预警学院, 湖北武汉 430019; 2.中国人民解放军31433部队, 辽宁沈阳 110000)
0 引言
线性调频连续波(LFMCW)雷达具有体积小、重量轻、功耗低等优势,因此被广泛用于SAR/ISAR成像系统,基于LFMCW雷达的成像方法已经引起了学者们的广泛关注[1-3]。直升机作为具备对地打击和运送能力的灵活飞行器,是一类典型的“低慢小”空中目标,因此基于LFMCW雷达实现直升机目标的检测与识别具有重要的意义。
本文的主要工作是完成LFMCW雷达的平动补偿方法研究,为后续的直升机旋翼成像以及微动特征提取奠定基础。LFMCW雷达在整个发射周期内都发射脉冲,这个特点导致了传统脉冲体制雷达的“走-停”模式不再适用,建模时必须考虑直升机在脉冲内的运动,此时如果将传统算法用于LFMCW雷达,将导致距离向的主瓣展宽[3],从而影响成像结果。因此,必须对LFMCW雷达的目标脉内运动进行补偿,其中一种较为常见的思路是参数类补偿方法,这类方法首先估计出目标运动参数,并对回波进行精确补偿,从而完成目标成像。基于这种思想,文献[3]使用了搜索算法,将图形对比度作为图像质量评价指标,对目标的运动参数进行了搜索并对目标进行了成像。该算法取得了较好的估计效果,但是由于该方法要对目标参数进行搜索,因此计算量较大。文献[4]使用了包络拟合的方法估计出目标参数,而后再进行平动补偿和方位成像,该方法首先提取出一维距离像的包络信息,而后在此基础上通过拟合完成了参数估计。该方法具备一定的运动参数估计能力,但是当目标信噪比较低时该方法将失效。文献[5-7]提出了Radon-Fourier变换(RFT)算法,该算法通过相参积累,提高了低信噪比条件下的检测能力,但是该方法也是沿着速度和距离的二维搜索,因此计算量也相对较大。
本文给出了一种改进的RFT算法实现运动补偿。通过粗搜索和精搜索的两步估计方法,在保证估计效果不受影响的前提下,降低了算法计算量。并通过仿真和对比实验验证了本文方法的有效性。
1 LFMCW雷达直升机回波建模
假设雷达到目标的距离满足远场条件,雷达到旋翼中心的距离为RC,直升机与雷达俯仰角为β,旋翼以恒定的角速度ω=2πfrot绕旋翼中心旋转(frot为旋翼旋转频率),如图1(a)所示。为了便于分析,考虑β=0°的情况,即此时雷达、旋翼都投影到一个平面内,如图1(b)所示。旋翼某一个叶片上的散射点P到旋翼中心的距离为r(0≤r≤l,l为叶片长度),P点到雷达的距离为RP,P点以角速度ω绕C旋转,初始时刻P点的初始旋转角为θ。目标的旋转中心C点位于x轴上,其初始坐标为(xC,0)。选取C为参考点,即Rref=RC。
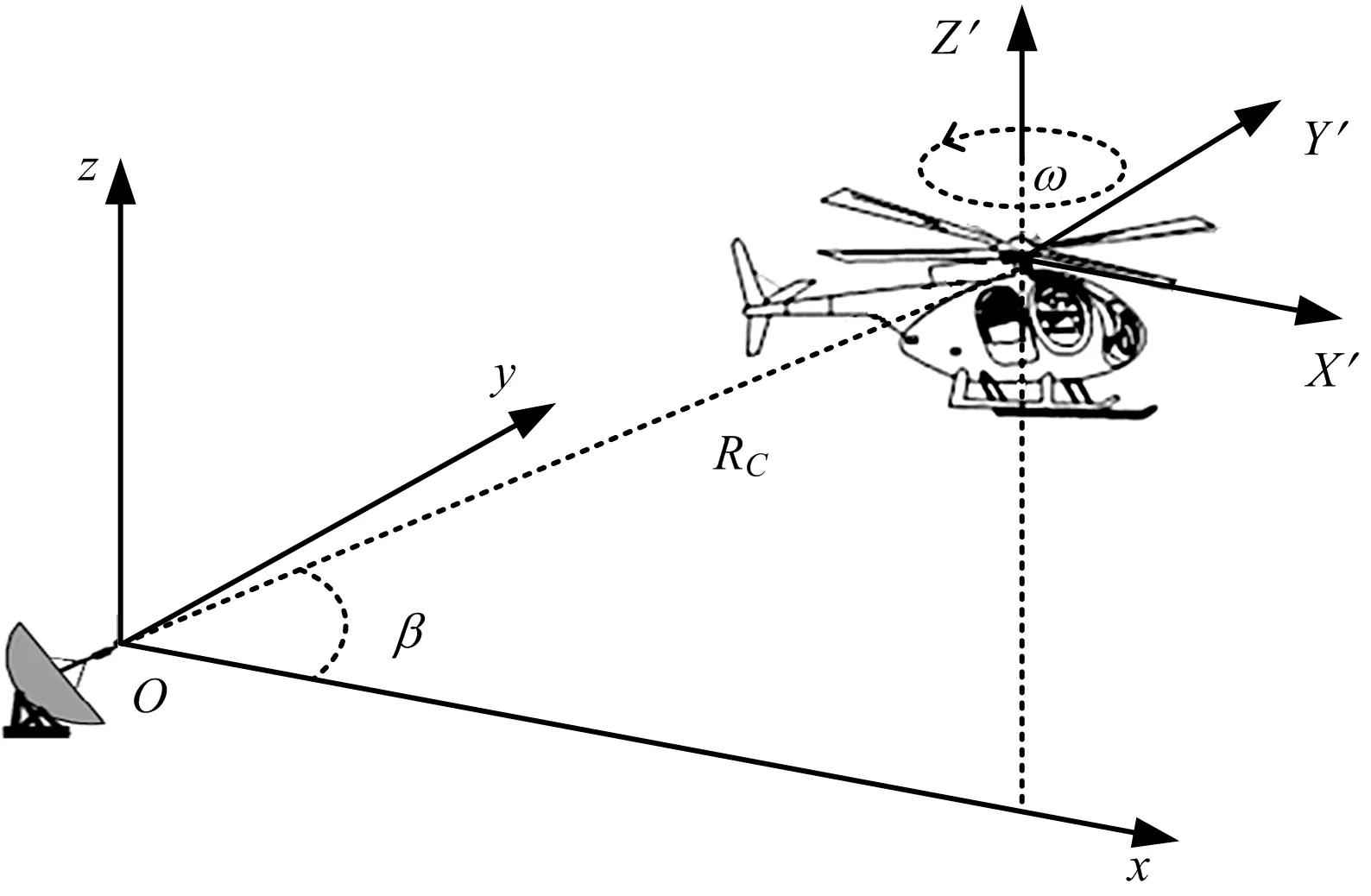
(a) 直升机与雷达在空间中的位置关系
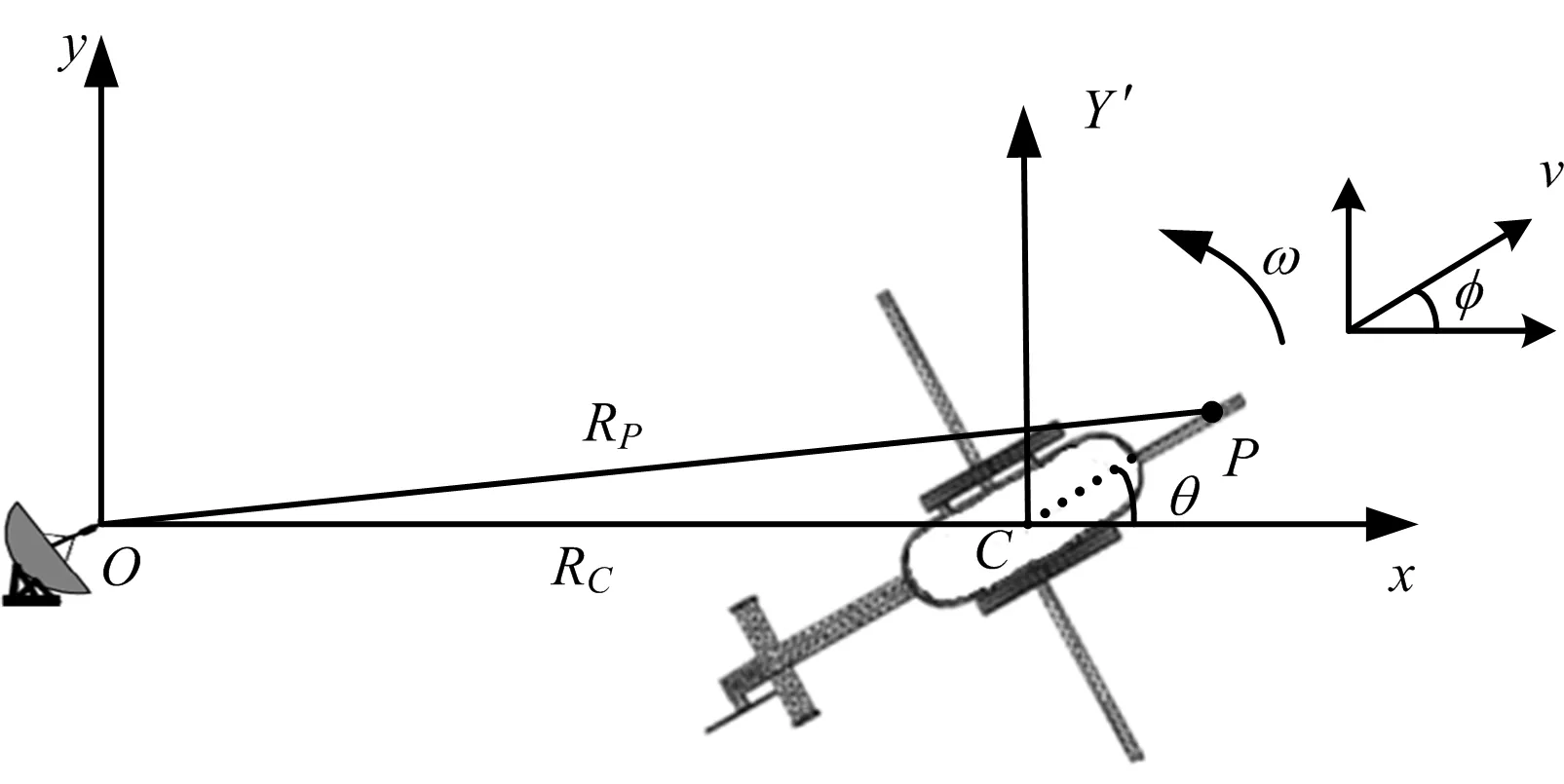
(b) 直升机与雷达在平面中的位置关系图1 直升机与雷达关系示意图
(1)
RQ(t)=R′(t)+xQ-yQωQt
(2)
式中,R′(t)为直升机沿雷达径向距离的函数,为散射点平动部分,xP,yP为旋翼上的散射点位置坐标,xQ,yQ为直升机机体散射点位置坐标,ωP为直升机旋翼的转速,ωQ为直升机机体等效为转台的角速度;可以看出,对于直升机旋翼和直升机机体,两者的平动部分表达式是相同的。因此,平动补偿只需要补偿掉两者相同平动的部分即可。下面分析直升机沿雷达径向距离的函数R′(t)。
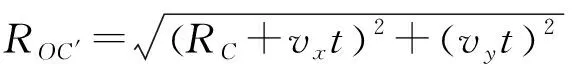
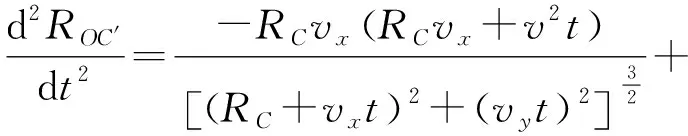
由泰勒公式展开,并取前三项,R′(t)可以近似表示为

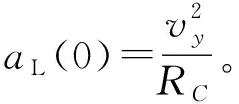
由式(5)可以得知,雷达径向方向上存在速度和加速度的影响。当直升机沿固定方向匀速直线运动时,会在雷达径向出现速度以及加速度,但是加速度分量较小,可认为对于一维距离像的平动无影响。例如当直升机航向与雷达视线方向垂直时(此时加速度最大),直升机速度为70 m/s,目标距离为20 km时,观测时间为2 s,雷达带宽为500 MHz(距离分辨率为0.3 m),此时的加速度为0.183 8 m/s2,由加速度引起的走动距离为0.367 5 m。因此对于直升机目标来说,其加速度对于一维距离像走动的影响并不明显,在对速度进行估计的时候可以不考虑加速度的影响。但是加速度对于相位的影响不能忽略,加速度会使得直升机机体成像时方位像上的散焦,必须将加速度带来的相位误差进行补偿,加速度引起的相位误差补偿方法在第2节进行说明。下面对回波信号进行分析。
本文雷达信号为LFMCW信号,雷达回波为
(6)
参考信号为
式中,τref为参考时间,τref=2Rref/c。回波与参考信号作Dechirp处理,得到的中频信号为
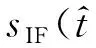
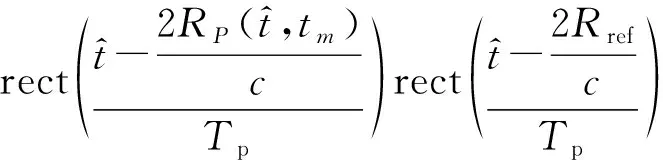
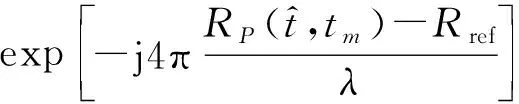
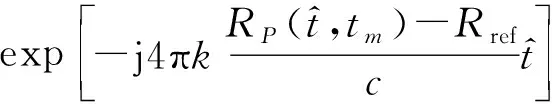
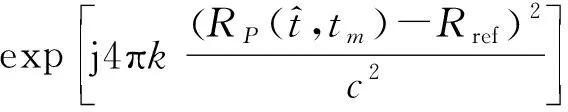
式中:第1项指数项为多普勒项,它包含了目标的多普勒信息;第2项为距离走动项,它包含了目标在雷达上的走动信息;第3项指数项为RVP项,它在LFMCW雷达中可被补偿[9];第4项为相位影响项,它使得目标回波的多普勒频率和距离信息都产生了变化,估计得到目标速度后可以对其进行补偿。
可以看出,由于LFMCW雷达时宽较大,目标在脉内的运动不能被忽略,导致了脉压后一维距离像主瓣的展宽[3],使得传统成像方法效果变差。为了解决该问题,需要对相位进行精确补偿。下面,本文提出一种改进的RFT方法来完成平动补偿。
2 基于改进RFT算法的目标速度估计与补偿方法
RFT方法是用于低信噪比条件下目标检测的一种有效工具,它可以实现在低信噪比条件下的目标检测。RFT利用速度与多普勒的关系进行相位补偿,并沿运动轨迹进行相参积累,其表达式[5]为
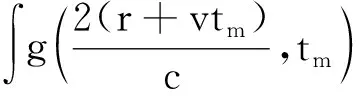
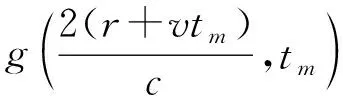
2.1 基于改进Radon-Fourier变换的运动参数粗估计
RFT算法的实现是采用先Radon变换对原始信号空间绕中心旋转,然后沿慢时间进行多普勒滤波,从而实现相参积累[10]。Radon变换旋转的角度对应着目标的速度,当旋转的角度为θ时,对应的速度v(θ)为
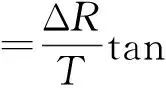
(10)
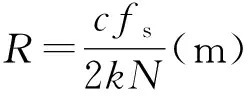
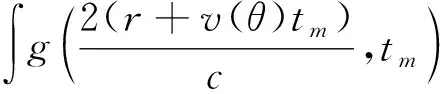
而后,沿着慢时间方向进行相参积累,并记录下此时不同距离对应的峰值W(θ):
W(θ)=maxrG(r,θ)
(12)
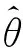

(13)
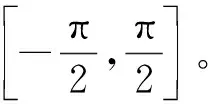
改进的RFT变换示意图如图2所示。通过RFT变换,不同目标上的散射点将会进行相参积累,由于目标主体上所有散射点的平动成分是相同的,因此对于一维距离像RFT变换进行积累可以得到若干个θ坐标相同、r坐标不同的点。
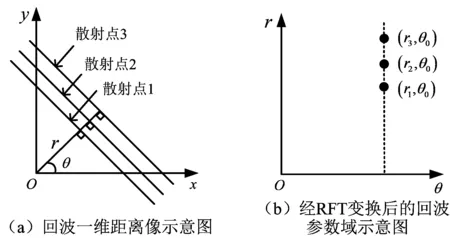
图2 改进RFT算法示意图
2.2 基于Tsallis熵的平动速度精估计
巴西物理学家C.Tsallis提出了一种广义的非广延熵,即Tsallis熵。Tsallis熵通过选择合适的非广延参数使得原先广延统计无法解释的现象得到了解决。文献[11]中通过分析和对比,得到了Tsallis熵比Shannon熵更加适应ISAR相位补偿这样的非广延系统的结论,因此本节引入Tsallis熵进行速度的精估计,Tsallis熵定义[11]为
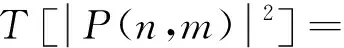
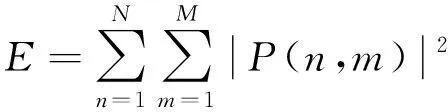
由得到的速度粗估计结果,首先对Dechirp后的回波进行平动补偿,补偿项为
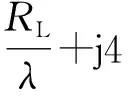
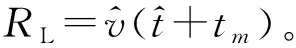
S=SIF·H
(17)
然后对该信号进行脉压,并进行方位成像后,最终的图像可以表示为
P=FFT2[FFT1S]
(18)
式中,FFT1·表示对距离向进行傅里叶变换,FFT2·表示对方位向进行傅里叶变换。

2.3 速度估计误差和加速度的相位校正
完成速度估计后,可以通过式(16)对LFMCW雷达Dechirp的回波进行补偿。但是补偿完成后相位中仍有补偿不完全的部分。其中一方面是由速度估计误差导致的,另一方面是由于加速度对相位的影响造成的。此时的相位项中包含的相位为
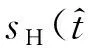
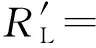
补偿完成后,可利用CEMD[13]等算法对回波进行分离,进而完成对旋翼和机体的成像,完整的流程如图3所示。
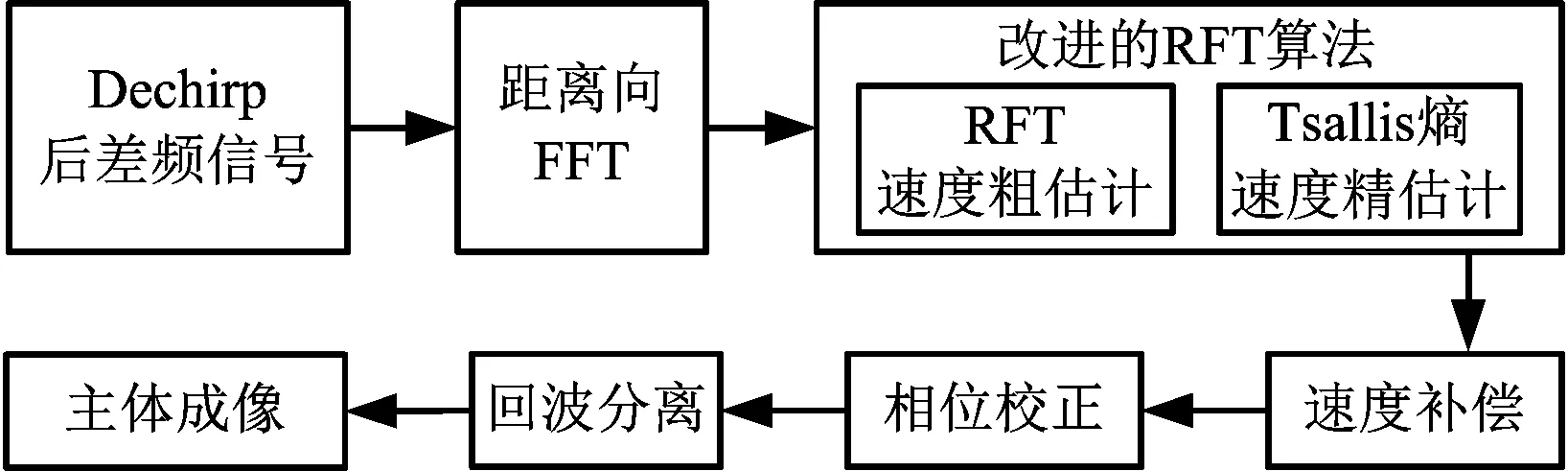
图3 速度估计与成像流程图
3 抗噪性能和计算量分析
本文定义的信噪比均为脉压后的信号功率与噪声功率的比值。假设脉压后的噪声为高斯白噪声,定义为
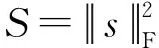
3.1 抗噪性能分析
在速度的粗估计中,对速度v进行了搜索,搜索的同时沿回波慢时间方向进行了相参积累,最终通过积累峰值判断出速度的估计值,其中相参积累使用的是FFT算法;在速度的精估计中,基于Tsallis熵进行了速度的搜索,通过边搜索边方位成像的方法确定了速度的精估计结果,其中方位成像时经过FFT算法后信号将相参积累,由于信号是离散的,FFT后的幅度与采样点数相关,积累后信号对应的幅值将变为AM,此时信噪比将变为

可以看到,不管是粗估计还是精估计,它们的信噪比都会得到20lgMdB的提升。通过理论分析可以说明本文方法具有在低信噪比条件下对飞机速度进行估计的能力。
3.2 计算量分析
根据文献[7]的分析,基于FFT算法的RFT计算复杂度为Nr5Jlog2(Nr)+18M+15Nv+10Jlog2(J),其中,Nr,Nv分别为距离搜索单元个数和速度搜索单元个数,M为回波方位向采样点数,J=M+Nv。本文的改进方法中,相当于减少了对速度的搜索,如果减少搜索量为γ,那么改进算法的计算复杂度将比原有的复杂度有所降低。但改进后由于加入了精搜索,因此还需精搜索部分的计算量。精搜索的计算量为L×N× log2M,其中N为距离像采样点数,L为精搜索的搜索次数。例如,若Nr=Nv=M=N=500,γ=400,L=400时,RFT算法的计算量为8.05× 107,改进RFT算法的计算量为4.82×107,效率提升了41.12%。
4 仿真与分析
本文所有实验均在操作系统为Windows 7的计算机上实现的,仿真平台为Matlab R2008b,计算机主要参数如下:处理器为Intel酷睿E7500,主频为2.93 GHz,内存为2 GB。仿真内容为基于LFMCW雷达的直升机速度估计。直升机模型和旋翼叶片模型如图4所示。雷达载频为10 GHz,脉冲宽度为2 ms,带宽为500 MHz,观测时间为1 s,噪声为脉压后添加的高斯白噪声。仿真分两部分,第一部分的仿真内容为传统成像方法(非参数类)与本文方法(参数类)的成像效果对比;第二部分的仿真内容为本文方法与其他参数类方法在计算量、估计精度上的对比。
本文选用某型直升机作为仿真对象。直升机机身长度为20 m,旋翼半径为10 m,旋翼转速为4 rad/s(对应的角速度为8π rad/s)。直升机速度为70 m/s,雷达距离目标20 km,航向与雷达视线方向成60°(直升机径向速度为35 m/s,径向加速度为0.183 8 m/s2)。散射点模型如图4所示。
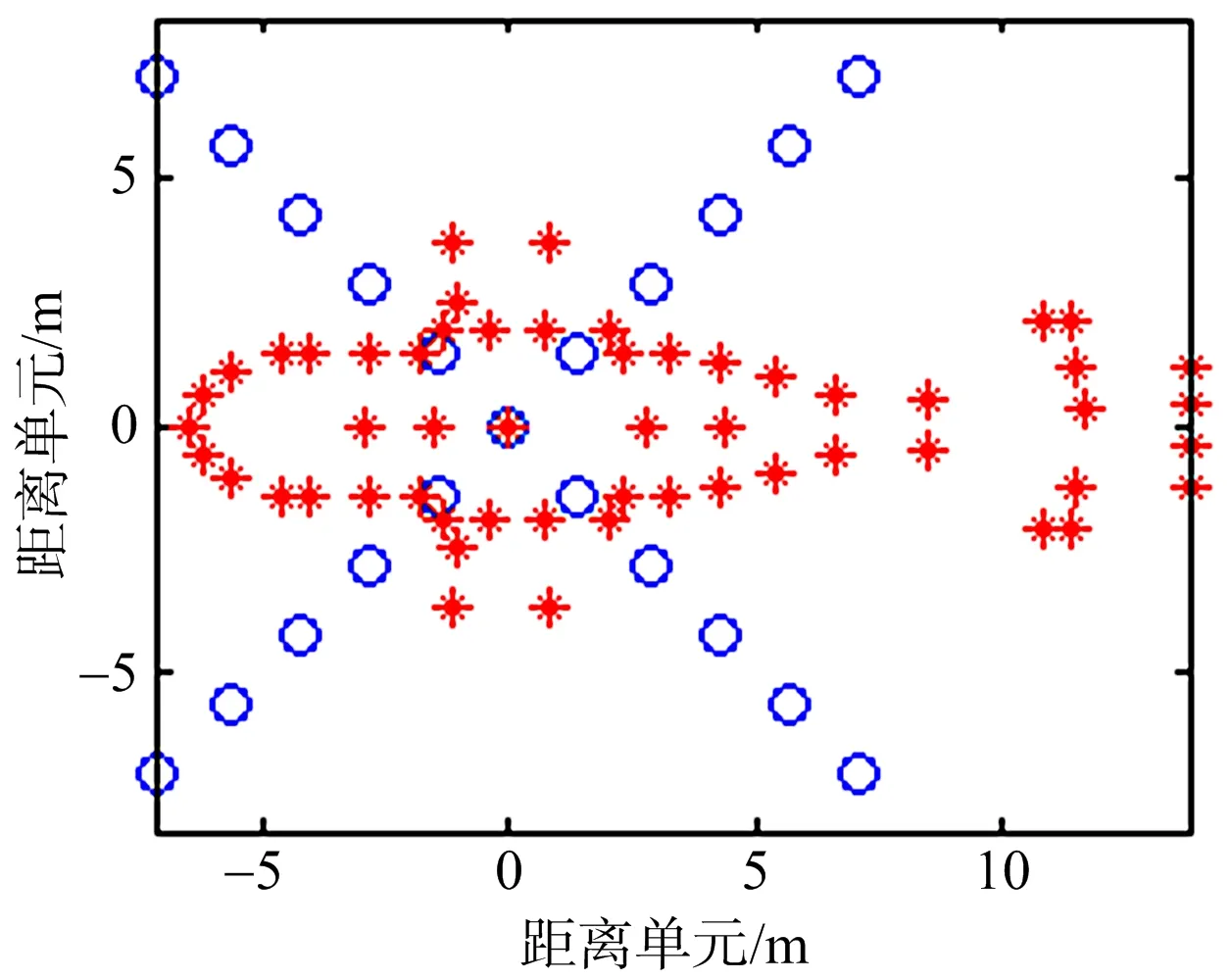
图4 某型直升机的散射点模型
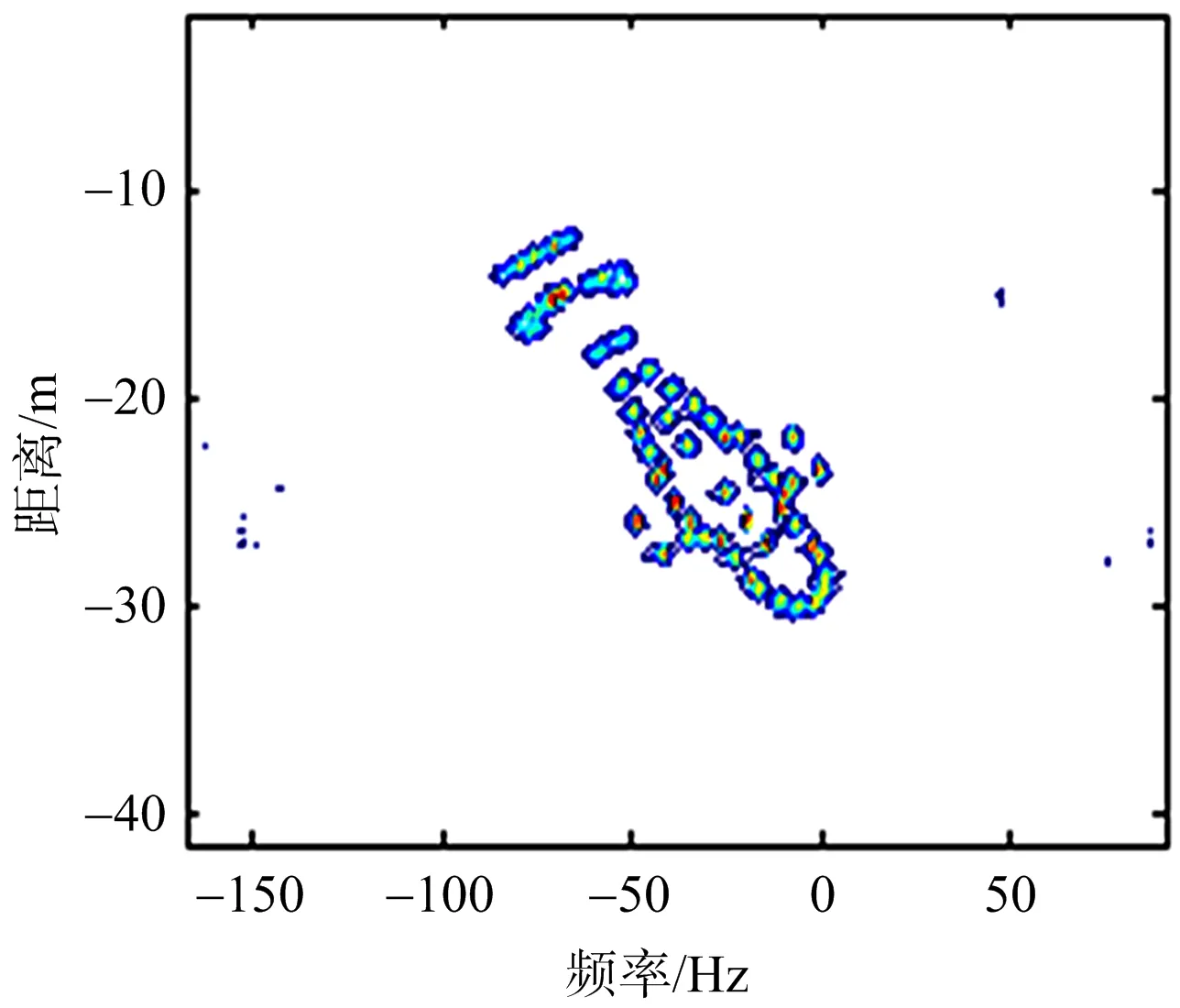
(a) 传统方法1(熵值9.42)
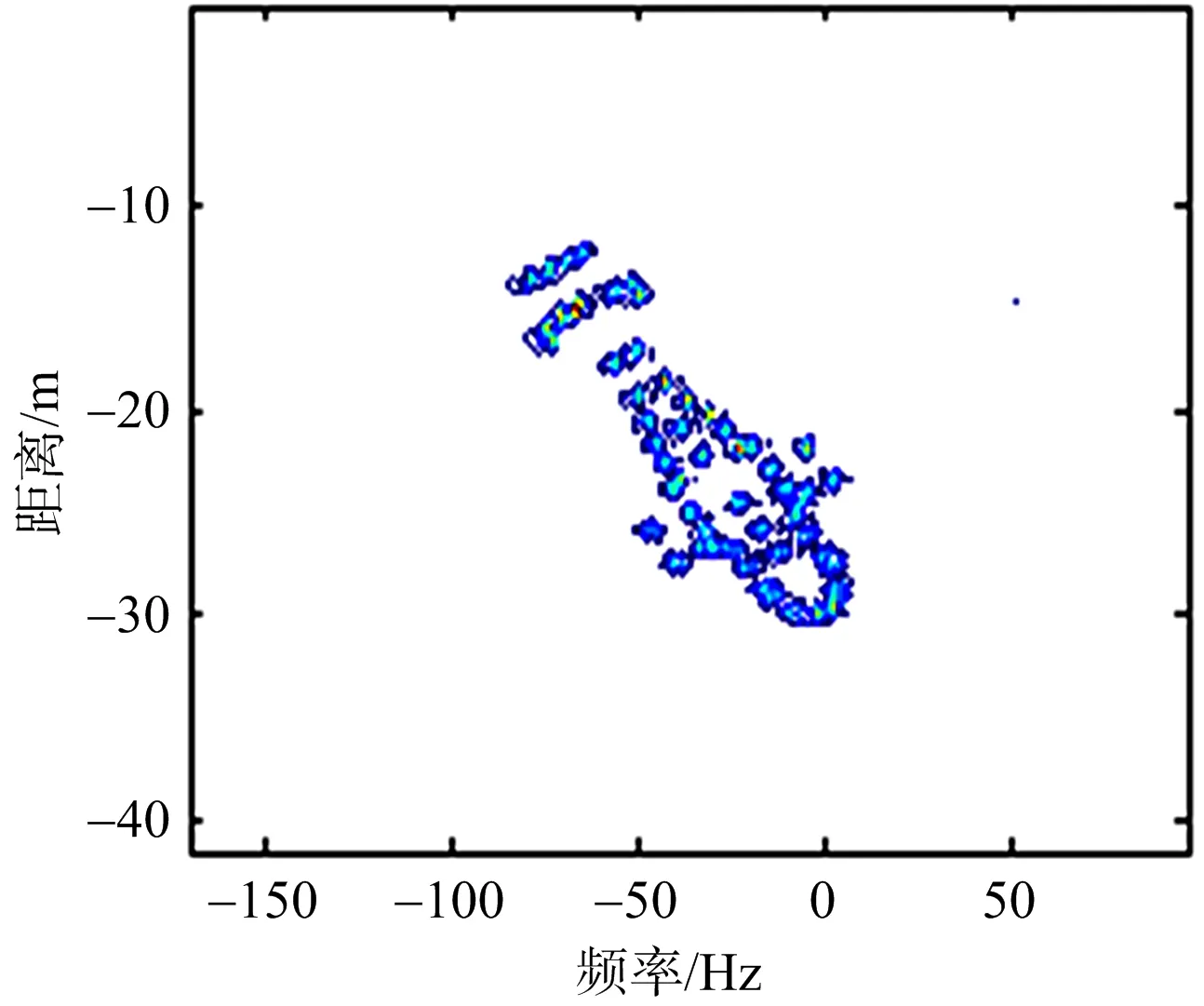
(b) 传统方法2(熵值9.48)
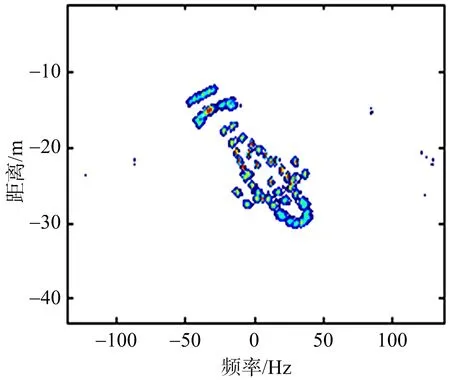
(c) 传统方法3(熵值9.43)
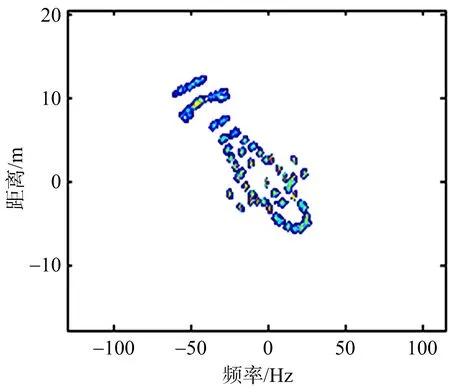
(d) 本文成像结果(熵值8.01)图5 传统成像方法成像效果及熵值
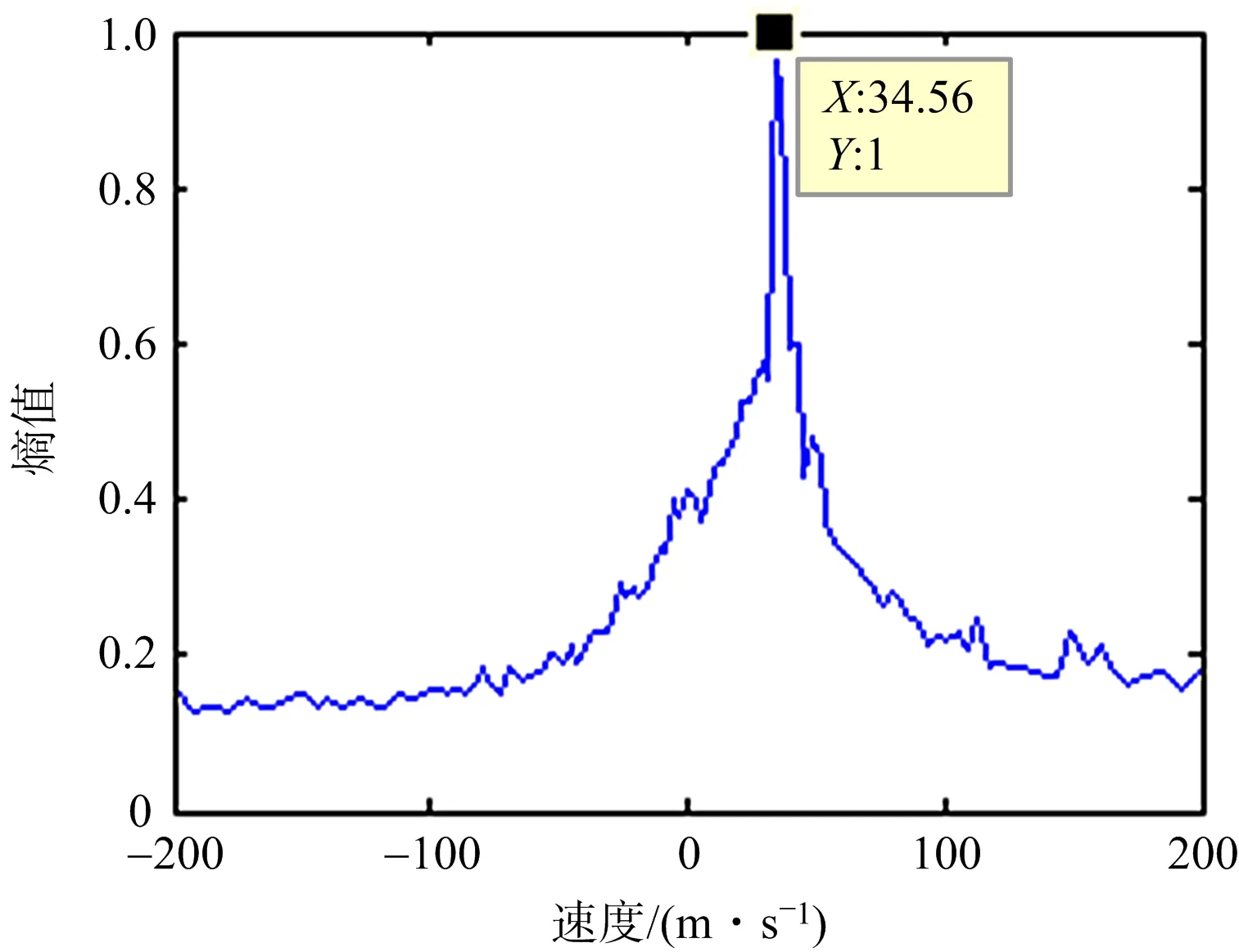
(a) 改进RFT变换粗估计结果
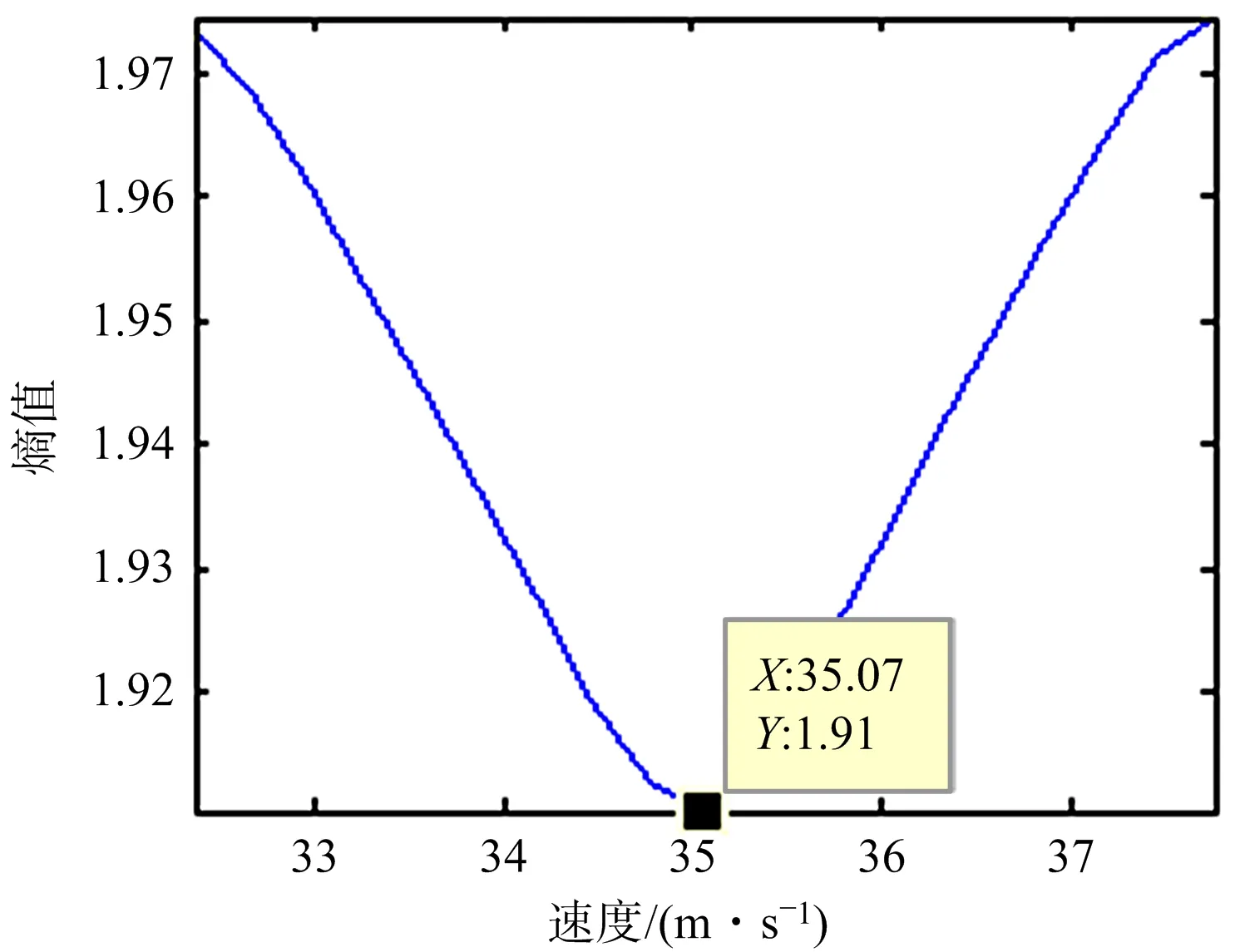
(b) Tsallis熵搜索精估计结果图6 速度估计和成像结果
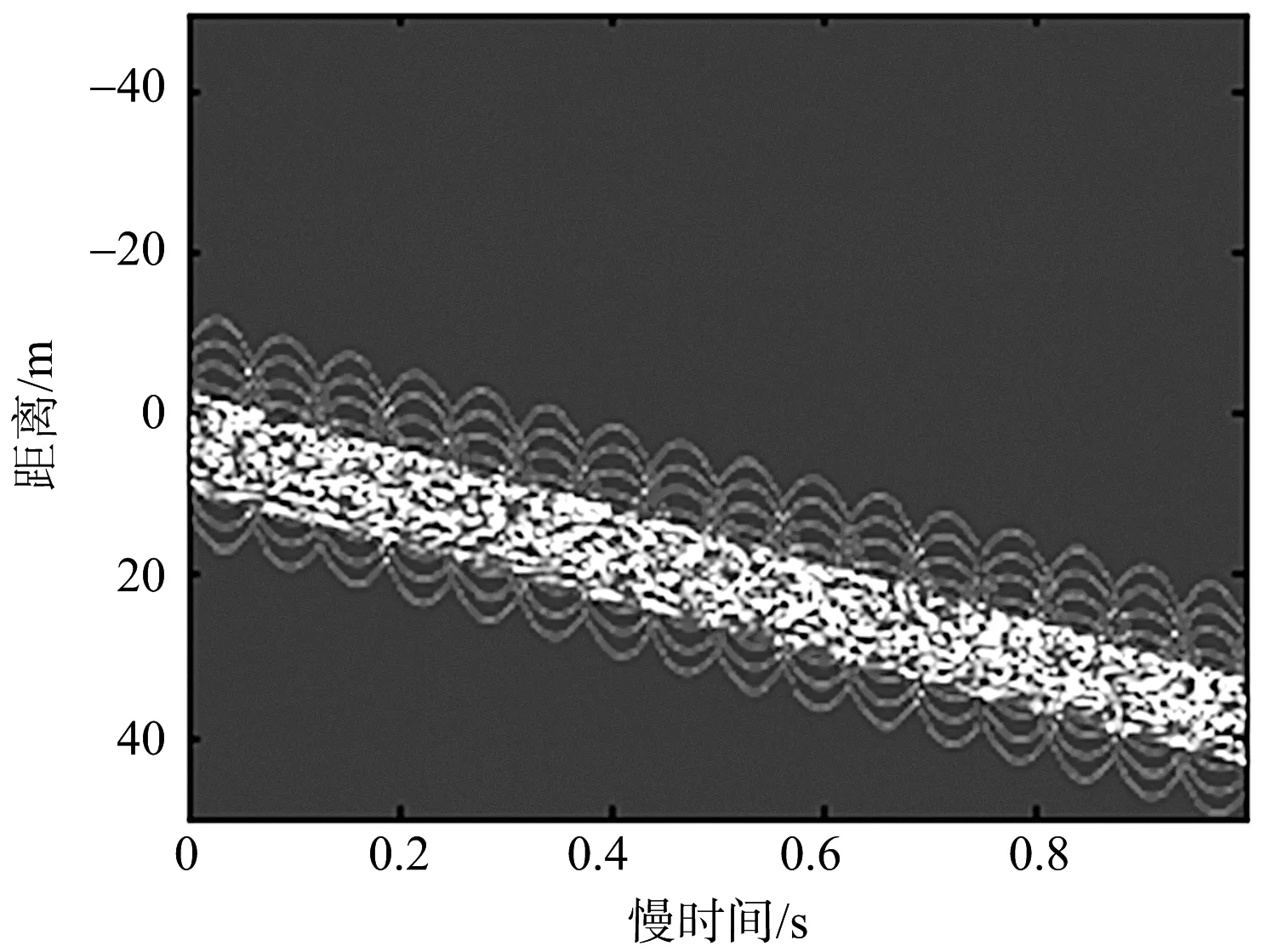
(a) 未运动补偿的一维距离像
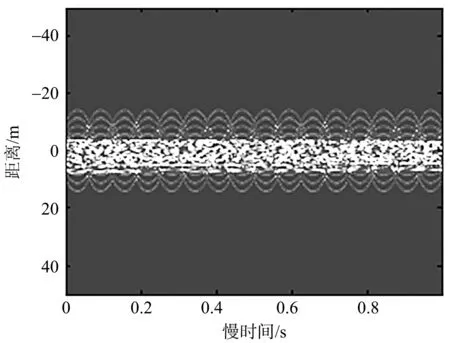
(b) 运动补偿后的一维距离像图7 运动补偿结果
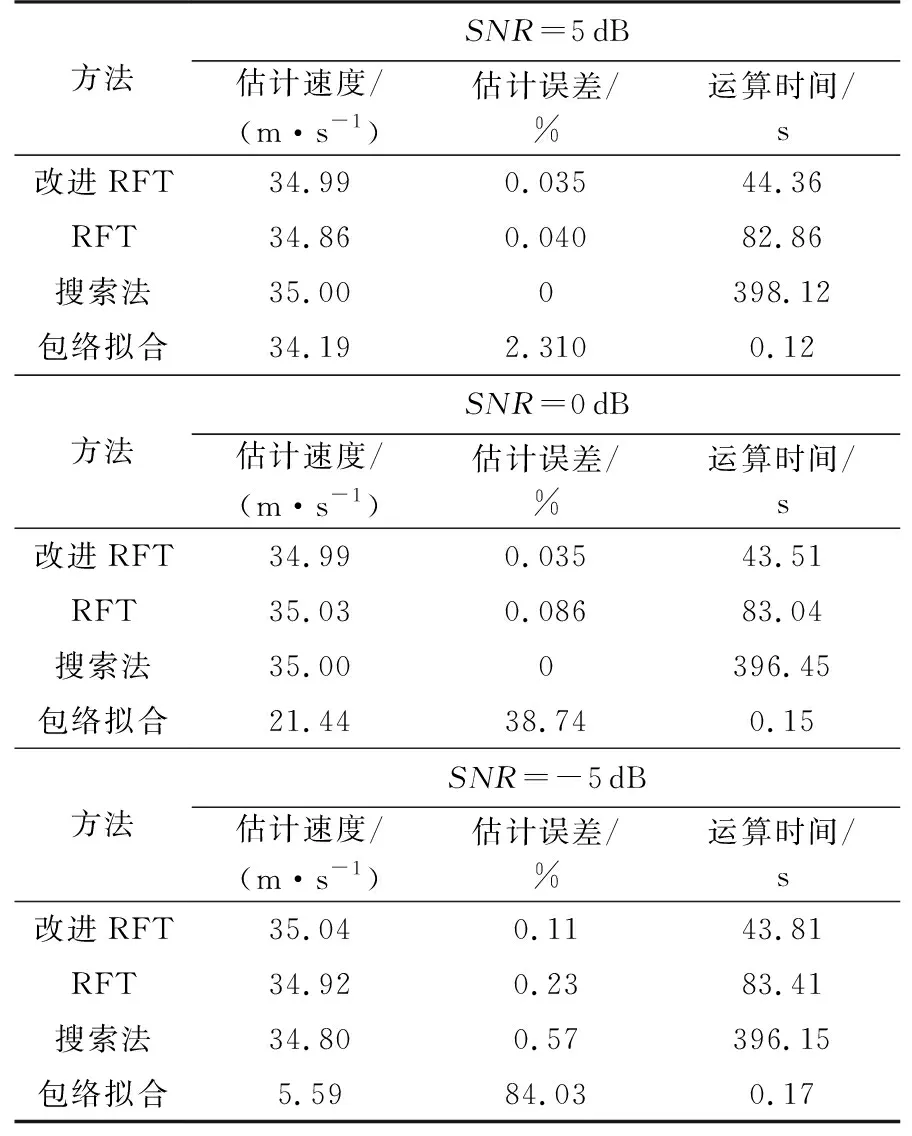
方法SNR=5dB估计速度/(m·s-1)估计误差/%运算时间/s改进RFT34.990.03544.36RFT34.860.04082.86搜索法35.000398.12包络拟合34.192.3100.12方法SNR=0dB估计速度/(m·s-1)估计误差/%运算时间/s改进RFT34.990.03543.51RFT35.030.08683.04搜索法35.000396.45包络拟合21.4438.740.15方法SNR=-5dB估计速度/(m·s-1)估计误差/%运算时间/s改进RFT35.040.1143.81RFT34.920.2383.41搜索法34.800.57396.15包络拟合5.5984.030.17
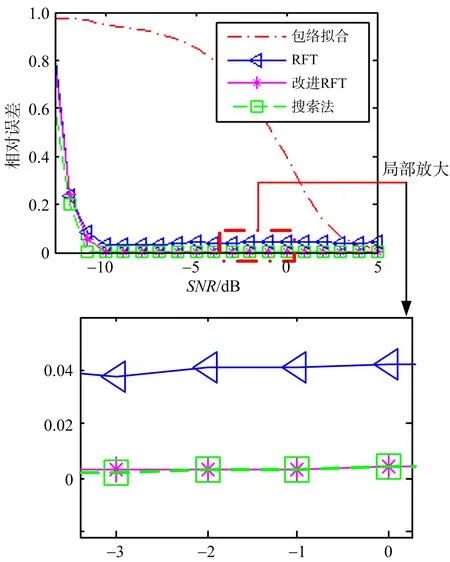
图8 传统算法与本文算法在不同信噪比条件下的误差
5 结束语
本文针对脉冲体制雷达的非参数类平动补偿方法不能完全应用到LFMCW雷达中的问题,提出了一种基于改进RFT算法的参数类补偿方法。首先,基于改进RFT算法进行了速度的粗估计,并在此基础上得到了速度的误差范围;其次,基于Tsallis熵对成像结果进行了搜索,当熵值最小时得到了速度的精确估计结果,并用该值构建补偿函数对回波进行补偿;最后,通过相位校正修正了速度估计误差和加速度对于相位的影响。该方法在不降低原有方法抗噪性能的同时,减少了计算量,提升了算法效率,为后续的LFMCW雷达微动特征提取奠定了基础。

