层流条件下并列三圆柱涡激振动响应与尾流形态

徐晓黎， 及春宁， 张 力， 陈威霖

（天津大学 建筑工程学院 水利工程仿真与安全国家重点实验室，天津300072）

1 引 言

圆柱结构常见于工程实例中，如海底管道等。流过圆柱的流体会引发结构振动，引起结构疲劳，降低结构寿命。

单圆柱在均匀来流中的涡激振动问题研究较多［1－3］。Williamson等［4］归纳了单圆柱涡激振动中出现的尾涡形态，将其分为2P，2S和P＋S三种形态。Ji等［5］应用虚拟区域法对单圆柱涡激振动进行了研究，雷诺数Re＝60～300，发现振动响应由初始和下端分支组成，尾流为2S形态。对并列双圆柱尾流形态的研究也获得了不少成果。Alam等［6］通过风洞实验对间距比T／D＝1．0～5．0的并列方柱绕流进行了研究，发现了单体尾流、窄－宽尾流、过渡尾流和涡街耦合尾流共4个不同的尾流形态。Supradeepan等［7］研究了 Re＝100，T／D＝1．1～8．0时并列圆柱的尾流形态，发现了单体周期、非周期、调制、反相同步和同相同步形态共5种不同的尾流形态。

振动的圆柱会与周围流体发生复杂的耦合作用，对应的流场会更复杂。Chen等［8］在Re＝100，T／D＝2．0～5．0条件下，并列双圆柱涡激振动的数值模拟中确认了6种不同的尾流形态。Xu等［9］研究了并列双圆柱的受迫振动，其中Re＝200，T／D＝1．2～3．2。发现只有振幅足够大时，振动和脱涡才能实现同步。Bao等［10］研究了Re＝100，T／D＝1．2～4．0时并列双圆柱的受迫振动，发现了5种不同的尾流形态。

单双圆柱涡激振动的研究取得了很多成果［11－13］，但三圆柱的研究较少。Zhou［14］在并列三圆柱（T／D＝1．5）绕流的研究中发现了窄－宽－窄尾流。Harichandan等［15］发现雷诺数和间距比是影响并列圆柱尾流形态转换的核心因素。Kang［16］在Re＝100条件下等间距并列三圆柱绕流中，发现了单涡街、偏斜、FF（Flip－Flopping）、同相同步和调制尾流共5种不同的尾流形态。Han等［17］在Re＝40～160条件下并列三圆柱绕流中发现了8种不同的尾流形态。

本文选取5个间距比（T／D＝2．0，2．5，3．0，4．0和5．0），对并列三圆柱的涡激振动进行数值模拟研究，深入分析振动响应的变化，根据泄涡和升力相位差等对尾流形态进行了归纳，并分析了原因。

2 数值模拟方法

2．1 流动控制方程

采用基于压强－力迭代的浸入边界法模拟流体运动，控制方程为

式中u为速度矢量，p为压强标量，f为附加体积力矢量，物理上代表了流体和固体之间的相互作用力，ν为流体运动粘滞系数，t为时间， 为梯度算子。

应用时间精度为二阶的Adams－Bashforth格式离散流动控制方程，得到守恒形式的控制方程为

式中h＝ ·［－uu＋ν（ u＋ uT）］，由粘性扩散项和对流项构成，T是矩阵转置符号，附加体积力f为

式中Vn＋1为固体边界的速度矢量，通过求解固体运动／变形方程得到，I和D分别为插值和分配函数，上标n＋1，n＋1／2，n和n－1为时间步。

由于浸入边界法控制方程为隐式，显式求解的精度不高。针对此情况，Ji等［18］将浸入边界法中附加体积力的求解嵌入到压强泊松方程的迭代求解中，提出了基于嵌入式压强－力迭代的浸入边界法。由于迭代过程中压强逐渐收敛于物理解，迭代修正的附加体积力也趋于真实值，该方法具有较高精度，且不会显著降低计算效率。该方法的具体介绍参考文献［18］。

2．2 问题描述

并列三圆柱等间距排列，且仅能横向振动。相关参数为，雷诺数 Re＝100；折合流速Ur＝U∞／fnD＝2．0～10．0，其中，U∞为来流速度，fn为圆柱的自然频率，D为圆柱直径；质量比m＊＝4m／（ρfπD2）＝2．0；计算域大小为200D（流向）和300D（横向）；对应的阻流比为B＝3D／H＝0．01。采用正交笛卡尔网格划分计算区域，流向和横向的网格数为1152×1280。圆柱周围为均匀加密网格，无量纲尺寸为Δx／D＝Δy／D＝1／64，加密区大小为4．0D×10．0D，如图1所示。（当T／D＞3．0时，加密区增大为4．0D×14．0D）。

数值模拟的边界条件为，左侧入口为狄利克雷型边界（u＝U∞，v＝0），右侧出口为纽曼型边界（ɸu／ɸx＝0，ɸv／ɸx＝0），上下为可滑移边界。

图1 计算区域大小和边界条件Fig．1 Illustration of the computational domain size and the boundary conditions

数值模拟的时间步长满足库朗条件CFL＝U∞Δt／Δx≤0．5。

3 验证算例

开展了并列三圆柱绕流数值模拟，并与其他文献结果进行比较，以验证本文所采用数值方法的正确性。算例中，三圆柱固定不动，其余参数与2．2节相同，表1对比了不同间距下的泻涡频率。发现由于阻流较小（本文为0．01，Kang［16］为0．03），本文的泻涡频率稍小于Kang［16］的结果，但两者的最大差别小于5%，从而验证了本文数值模拟方法的正确性。本文采用的计算程序已通过单／多圆柱绕流和单／多圆柱涡激振动的算例验证，可参考文献［11－13］。

4 结果与讨论

4．1 涡激振动响应

图2给出了不同间距比下圆柱响应的均方根值Yrms／D（以下简称振幅）。在各间距比下，圆柱振幅随折合流速的增加均呈现初始和下端分支。

表1 并列等间距三圆柱绕流的斯特劳哈数对比Tab．1 Comparison of the Strouhal number of flow past three equal－spaced sideby－side cylinders

对T／D＝2．0的工况，当Ur≤2．6时，三圆柱的振幅均很小；当Ur＞2．6时，圆柱振幅急剧上升；当Ur≥3．6时，圆柱2振幅小于圆柱1和3的振幅，仅在Ur＝4．6时，三圆柱振幅较接近。由于间距比较小，三圆柱间相互作用较强，当折合流速Ur≥5．0时，两个外侧圆柱（圆柱1和3）的振幅不相等，但差别较小，这与圆柱的不稳定振动以及偏斜的间隙流有关。此外，当Ur≥5．0时，圆柱1和3的振幅明显大于圆柱2。

对T／D＝2．5和T／D＝3．0的工况，圆柱间距稍大，相互作用减弱，三圆柱振幅变化较为平缓，比较规律。间距比T／D＝2．5的工况下，当Ur≤2．8时，三圆柱的振幅均很小；当Ur＞2．8时，圆柱振幅急剧上升，圆柱1和3的振幅基本相等，仅在个别折合流速范围内不相等；当Ur＞7．8时，圆柱2的振幅明显小于两侧圆柱。在T／D＝3．0的工况下，圆柱1和3在Ur＝4．2时取得最大振幅Yrms／D＝0．392，圆柱2在Ur＝4．6时取得最大振幅Yrms／D＝0．366。其他变化特征与T／D＝2．5的工况类似。

T／D＝4．0和T／D＝5．0工况下，两侧圆柱振幅相同，略大于中间圆柱。当T／D＝4．0时，圆柱1和3在Ur＝4．2时取得最大振幅Yrms／D＝0．392，圆柱2在Ur＝4．6时得到最大振幅Yrms／D＝0．371。当T／D＝5．0时，圆柱1与圆柱3在Ur＝4．4时取得最大振幅Yrms／D＝0．390，圆柱2此时也取得最大振幅Yrms／D＝0．376。

可以看出，随着间距比的增加，圆柱最大振幅不断减小，两侧圆柱的振动响应也趋于相同，且与中间圆柱的振幅相差更小。大间距比工况下（T／D＝5．0），圆柱的响应更趋于单圆柱涡激振动的情况。在间距比T／D＝2．0～4．0的工况下，圆柱2在初始和下端分支交界处出现振幅不连续现象。圆柱1和3仅在间距比T／D＝2．5的工况下出现振幅不连续现象。随着间距比的增加，振幅不连续现象所对应的折合流速逐渐增大，依次为Ur＝3．4，3．6～3．8和4．0。此现象的出现可能与临近圆柱的存在改变了圆柱的附加质量有关。

4．2 振动频率

图3给出了圆柱1、2和3在不同Ur和T／D下振动频率的变化。为使不同间距比的结果错落有致，间距比为2．0，2．5，3．0，4．0和5．0的振动频率分别以f＝0．0，0．2，0．4，0．6和0．8为零点。可以看出，圆柱1和3的振动频率基本一致；随着间距比的增加，圆柱2的振动频率逐渐接近于圆柱1和3；特别地，当Ur＞7．0时，圆柱2的频率稍大于圆柱1和3。

图2 不同间距比下振幅（Yrms／D）随折合流速的变化Fig．2 Root mean square value of vibration amplitude（Yrms／D）varying with Urat different spacing ratios

4．3 尾流形态

根据并列三圆柱后的尾涡，参考圆柱升力相位差等因素，将尾流分为图4所示的6种形态。

4．3．1 窄宽窄尾流形态

圆柱间的两个间隙流均偏向外侧，在圆柱后侧形成窄宽窄尾流形态。如图4（a）所示，圆柱2后侧形成宽尾流，圆柱1和3后侧形成窄尾流，三圆柱后的尾涡长度相当。旋涡之间相互配对融合，在下游形成杂乱无章的尾涡。

4．3．2 不规律尾流形态

此模式下旋涡脱落比较混乱，如图4（b）所示。在T／D＝2．0，Ur＝7．2的工况下，三个圆柱的泻涡频率均不相同，圆柱间升力相位差无规律变化，如图5（a）所示。

4．3．3 反相同步尾流形态

图3 不同折合流速Ur和间距比T／D下的振动频率f Fig．3 Vibration frequency（f）varying with Urand T／D

三圆柱的尾涡同步脱落，圆柱1和3与圆柱2的振动反相，称为反相同步尾流形态。以T／D＝3．0，Ur＝4．4为例，圆柱2后侧尾流宽于圆柱1和3。由于泻涡反相，且圆柱间距较大，尾流之间相互独立，不发生融合，在圆柱后侧形成3条2S涡街，如图4（c）所示。此时，圆柱1和3升力相位差集中在0°附近，而圆柱1和2以及圆柱2和3的相位差维持在180°附近，如图5（b）所示。该模式下的升力相位差波动很小，在T／D＝3．0时，圆柱间的相互作用减小，同步尾流形态可以稳定存在。此时间隙流向外侧两圆柱偏斜。圆柱2与圆柱1和3升力之间的相位差并不完全反相，而是维持在165°和195°左右。当圆柱3返回到平衡位置时，圆柱2尚未达到平衡位置，圆柱3旋涡脱落早于圆柱2。由于圆柱3旋涡附近的压强较低，吸引圆柱2旋涡向下偏移，形成向下偏斜的间隙流；圆柱1和2间的向上偏斜的间隙流成因相同。这与Chen等［8］对并列双圆柱涡激振动中的偏斜流形态的解释一致。

4．3．4 调制尾流形态

圆柱1和3的泻涡频率相同，与圆柱2的不同，圆柱2的尾流交替与圆柱1和3的尾流发生配对融合，这种尾流形态称为调制尾流形态。该尾流形态的重要参数为调制周期Tmodulation＝1／｜f1－f2｜（其中f1和f2分别为两圆柱的泻涡频率）。调制周期越大，调制作用越弱。

以T／D ＝4．0，Ur＝2．6的工况为例，如图4（d）所示，圆柱泻涡在近尾流形成三条平行2S涡街，但圆柱2的泻涡与圆柱3在远尾流配对融合。如图5（c）所示，圆柱间的升力相位差呈现出明显的调制周期，其值为Tmodulation≈166，约30个泻涡周期。圆柱1和3升力相位差为150°～210°，圆柱1和2的相位差在一个调制周期内不断减少，而圆柱2和3的相位差则不断增加。当折合流速增加到Ur＝4．0时，调制周期明显较小，Tmodulation≈84，如图5（d）所示。

图4 6种尾流形态Fig．4 Six wake patterns

4．3．5 同相同步尾流形态

此时三圆柱的尾涡同频同相脱落，中间圆柱的尾涡分别与两侧圆柱的尾涡配对融合，形成对称的尾流。如图4（e）所示，当T／D＝2．5，Ur＝5．6时，由于受圆柱1和3泻涡的影响，从圆柱2表面脱落的旋涡拉伸，分裂为两个大小不等的子涡，并分别与外侧圆柱的同向旋涡融合，在圆柱2后侧形成一列稳定且对称的涡街。如图5（e）所示，三圆柱间的升力相位差均在0°附近，说明三圆柱泻涡是同相同步的。

4．3．6 偏斜尾流形态

此时三圆柱的尾涡同频泻放，但呈现出明显的不对称性，尾流稳定地偏向一侧，形成稳定的偏斜流。以T／D ＝3．0，Ur＝5．8为例，如图4（f）所示，此时尾流呈现出明显的不对称性。由于受圆柱1和3泻涡的影响，从圆柱2表面脱落的旋涡拉伸，分裂为两个大小不等的子涡，并分别与圆柱1和3的同向旋涡融合。圆柱2的尾涡明显向上侧发生偏斜，并且偏斜的方向始终保持不变。三圆柱间的升力相位差维持在－10°～－30°范围内，如图5（f）所示。

4．3．7 尾流形态在T／D－Ur参数空间内的分布

根据泻涡频率和升力相位差，给出研究范围内的尾流形态在［T／D，Ur］内的分布，如图6所示。

窄宽窄尾流形态仅出现在间距比相对较小且折合流速较小的情况，即2＜T／D≤2．25，2．0≤Ur≤2．6。对应形态下，圆柱的振幅很小，圆柱1和3的泻涡频率相同，但与圆柱2不同。

不规律尾流形态下，三圆柱的泻涡频率均不相同。该尾流形态存在于四个区域。当间距较小时，该尾流形态出现在较大的参数范围；随着间距比的增加，出现的参数范围减小，集中在初始和下端分支的结合处；而在大间距比、大折合流速情况下，未出现该尾流形态，说明该尾流形态出现在圆柱间相互作用较强的工况中。

反相同步尾流形态出现的范围较广，小间距比时，对应较低折合流速2．6＜Ur≤3．2；大间距比时，对应较高折合流速4．2≤Ur≤6．2。在该模式下，三圆柱的泻涡频率相同，圆柱2和圆柱1或3的升力相位差维持在180°左右。

调制尾流形态所占的参数空间范围最广，多出现在大间距比和大折合流速的情况下。此时，圆柱1和3的泻涡频率相同，但与圆柱2不同。根据调制周期的大小，可判断调制作用的强弱。调制周期越小，调制作用越强，出现涡街融合；调制周期越大，调制作用越弱，涡街不融合。

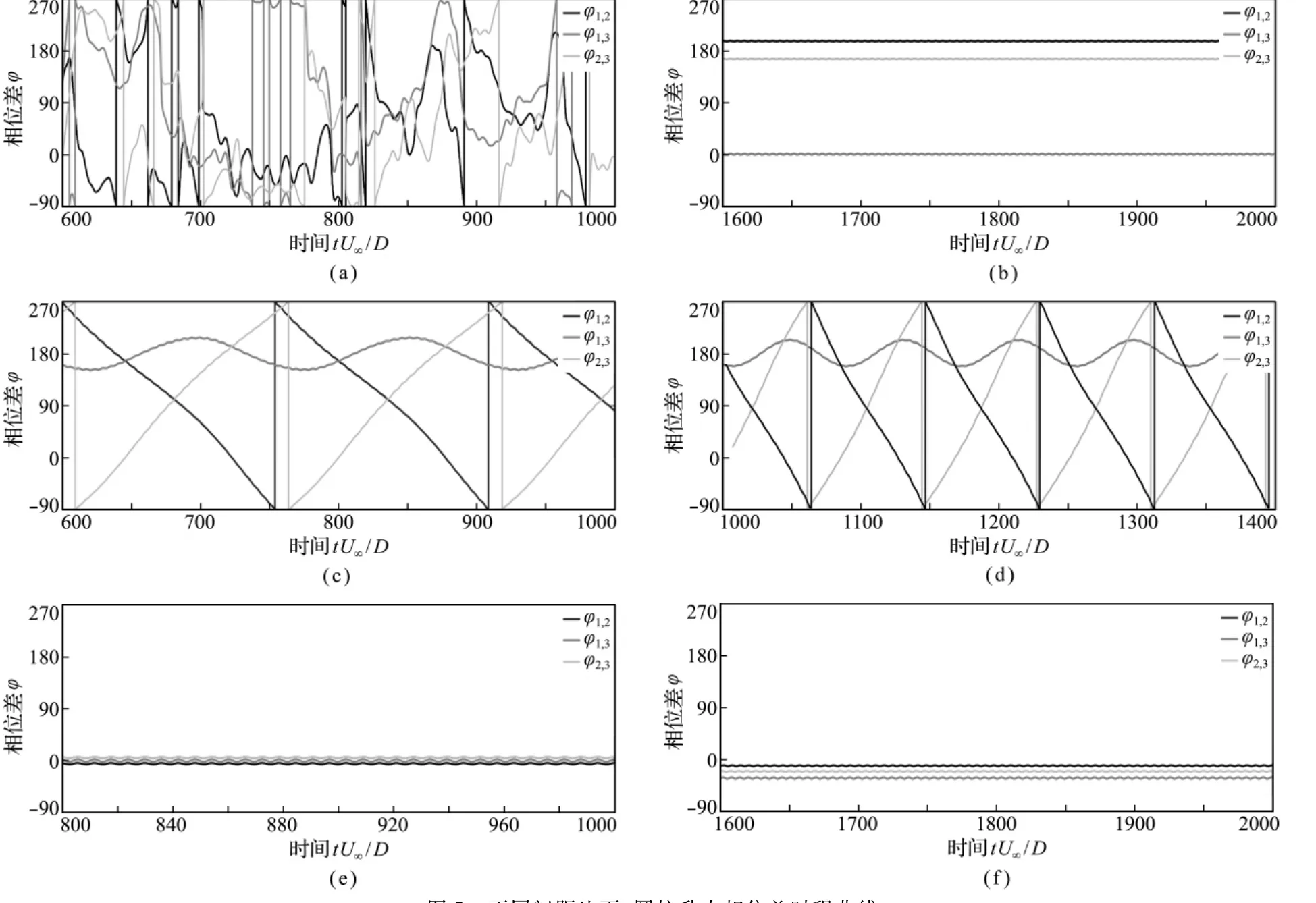
图5 不同间距比下，圆柱升力相位差时程曲线Fig．5 Time histories of the lift phase difference at different T／D

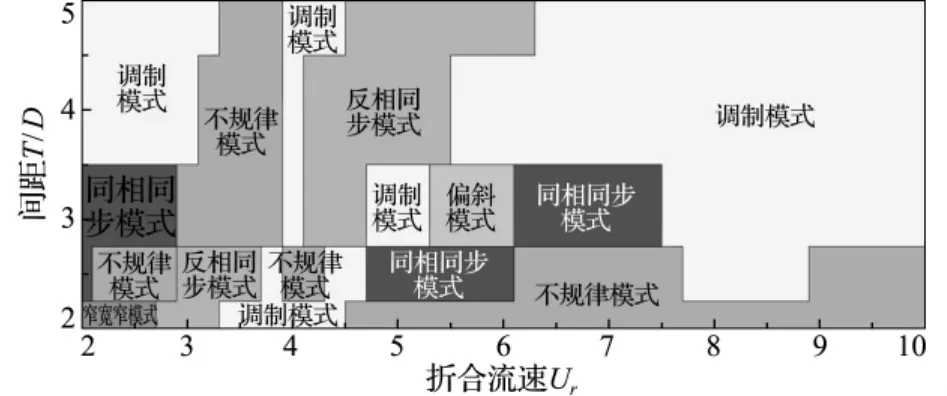
图6 尾流形态分布Fig．6 Distribution of the near－wake patterns

同相同步尾流形态多出现在中等间距比的情况下，即2．25＜T／D≤3．50，对应的折合流速范围分为2≤Ur≤2．8和4．8≤Ur≤7．4两个区域。此时三圆柱的泻涡频率相同，三圆柱间的升力相位差在0°左右。

偏斜尾流形态出现范围很小，仅在2．75＜T／D≤3．50和5．4≤Ur≤6．2范围内出现。此时，圆柱的振幅较大，三圆柱的泻涡频率相同，升力相位差在－10°～－30°范围内。

5 结 论

本文对层流条件下等间距并列三圆柱的涡激振动进行了数值模拟，主要结论如下。随折合流速增加，圆柱的振动响应表现为两个分支，即初始分支和下端分支。随着间距比的增加，最大均方根振幅逐渐减小。圆柱2在T／D＝2．0～4．0情况下出现振幅不连续现象，圆柱1和3仅在T／D＝2．5的情况下出现振幅不连续现象。随着间距比的增加，振幅不连续现象出现时所对应折合流速增大。

在研究的参数范围内共出现了6种尾流形态，分别为窄宽窄尾流，仅在小间距和小振幅时出现；不规律尾流，三圆柱的泻涡频率不相同；反相同步尾流，圆柱2与圆柱1和3的泻涡反相，圆柱1和3同相，此时圆柱2的尾涡宽于圆柱1和3，近尾流形成三条2S涡街；调制尾流，圆柱1和3的泻涡频率相同，但与圆柱2不同，使得圆柱泻涡发生周期调制；同相同步尾流，三圆柱尾涡同相同步泻放，圆柱2尾涡拉伸，并分别与外侧圆柱的同向旋涡融合，形成稳定且对称的涡街；偏斜尾流，与同相同步尾流类似，但尾流不对称，圆柱2的尾流明显偏向一侧且偏斜的方向保持不变。