应用于非凸设计区域桁架拓扑优化的一种基结构生成方法

史 航， 高 阁， 谢 军， 郭煜晨， 王 涛， 刘震宇＊

（1．中国科学院 长春光学精密机械与物理研究所，长春130033；2．中国科学院大学 材料科学与光电技术学院，北京100039）

1 引 言

拓扑优化是现代工程中一个重要发展领域，可以分为连续体拓扑优化和离散体拓扑优化，其中连续体拓扑优化主要研究二维板壳和三维实体等结构内有无孔洞、孔洞的数量、位置及形状；离散体拓扑优化大多数情况是指桁架拓扑优化，主要研究桁架和刚架等结构中杆件的有无及其相互连接方式。在桁架拓扑优化领域，最主要的一种实现方法是基结构法。即在特定设计区域内生成满连接结构，并且默认最优解就在其中，再通过优化算法找到最终的最优组合［1－3］。基结构法是由 Dorn等［4］在20世纪中期提出，之后广泛地应用于桁架的拓扑优化问题。运用基结构法求解桁架拓扑优化问题的初始步骤是在定义的设计区域中生成初始基结构，所获得的最优解由初始基结构中节点的位置和节点之间的连接（杆件）决定。对于理论中常出现的规则设计区域，生成满连接基结构较易实现，可是在实际工程中经常会出现一些涉及不规则设计区域（凹区域和孔洞）的问题，就要避免在凹区域或孔洞内部生成杆件。关于基结构的生成方法有很多种，通过有限元网格与计算机辅助设计软件的结合使用，Simth［5］提出了一个可以在非凸设计区域生成基结构的交互系统，可以对复杂非规则形状的设计域高效构建基结构。Zhang［6］利用正方形网格和维诺图（Voronoi）网格的微元法生成基结构，这种方法可以大量避免重复杆件的生成，并且可以针对凹区域和孔洞生成基结构。在已生成的初始基结构中，根据Hagishita等［7］提出的五条规则对可能存在的杆件进行判别，从而通过删减杆件获得最终基结构的生长式基结构法。Zegard等［8］提出了利用分级生成基结构和设置限制区域的方法在任意二维设计区域生成最终的基结构，并提供了MATLAB程序。该方法对单元网格依赖比较小，且可以在全局范围内生成基结构，是目前应用最为广泛的一种方法。Gao等［9］发现如果通过应力迹线法生成节点，即将节点都设置在设计区域内的应力迹线交点上，可以很大程度上减少无用杆件的数量，从而提高整体的运算效率。

基结构的生成主要分为两步，即先生成节点，然后将所有节点相互连接生成基结构。这使得满连接基结构在不规则设计区域外也会存在杆件。目前，删除多余杆件的方法是受到碰撞检验算法的启发而得到的［10］，即将原有几何边界拓展形成拓展边界，进而对存在于区域外的杆件与拓展边界进行碰撞检测，将多余杆件删除。这种方法存在以下两个方面的问题。一是在原几何模型的基础上建立新几何模型，即要建立两次模型，使前期工作过于繁复；二是偏置区域的大小直接影响检测凹边界外杆件的精度，随着偏置程度大小的变化，检测到的凹边界外杆件的数量也随之改变。尤其在凹边界是曲线的情况下，由于在进行判断检测的过程中是利用线段近似逼近曲线，存在几何误差，因此不可避免地对最终基结构的杆件数目造成影响。

本文提出一种无需构建扩展边界模型，而是利用已有几何边界进行识别并删除多余杆件的方法。由于满基结构中杆件众多，所以通过分区域生成基结构，找出存在于设计区域内无需进行判断的杆件，从而使需要判断的杆件大幅度减少；再根据凹边界的几何信息确定删除杆件的准则，最终得到符合要求的基结构。本文的主要目的是研究基结构的生成方法，并对三种不同情况下拓扑结构的二维算例以及一个三维算例进行实现。为了简化问题，所有算例采用的数据都是单位1。

2 二维问题基结构的生成方法

2．1 用于生成基结构的有限元基础网格

首先定义文中出现的一些概念，以二维问题为例，如图1所示。

本文提出的基结构生成方法依赖于设计区域的几何边界以及网格划分。采用有限元商业软件COMSOL进行几何建模并划分有限元网格，其中节点信息、边界信息和单元信息可以定义边界和节点的连接方式，将生成和删除杆件的过程转换为线性代数的操作，为后续基结构的生成提供便利。

2．2 基结构的生成

生成非凸区域基结构需要先利用节点生成满连接基结构，在此基础上剔除位于设计区域外部的杆件，快速生成满连接基结构并且快速准确地识别这些需要剔除的杆件是基结构生成算法的核心内容。用一个L型非凸设计区域简要说明实现过程。

2．2．1 逐级生成满连接基结构

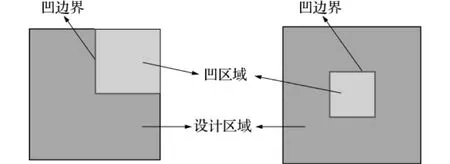
图1 二维非凸设计区域Fig．1 2Dnon－convex design domain

图2 为生成基结构步骤。首先将非凸设计区域划分为两个子区域，然后划分有限元网格，最后在此基础上建立满基结构。受GRAND方法［8］的启发，利用杆件连接等级的概念逐级建立杆件，如果两个节点属于同一单元，则称其是相邻的，两者连接成一级杆Lv1，如1节点和6节点相邻，bars16等级为Lv1；如果两个节点属于相邻的两个单元，则称其是相邻单元的相邻节点，如1节点和8节点，bar18等级为Lv2；以此类推，逐级形成基结构。在高等级的新生杆件中会包含重叠杆件，如bar58和bar25；且随着等级的升高，杆件的长度也逐渐变长，基结构法倾向于保留短杆，所以通过判断夹角余弦值的方法即共线检查方法来移除重叠长杆，为优化过程采用高效率算法提供了便利。

2．2．2 利用图形碰撞检测技术删除杆件

显而易见，bar37、bar27和bar38是设计区域外的杆件，一种情况是与凹边界edge47和edge34相交的bar27和bar38，另一种情况是两个端点都位于凹边界上的bar37，在此将一条线段端点落在另一条线段上这种情况视为不相交。延轴向包围盒是各个边（面）的法向与给定坐标轴平行的特殊长方形（体）［11］。以长方形为例，常见的一种方式是通过定义对角线的两个极值端点来定义包围区域，如图3所示，以线段AB为对角线建立的矩形区域即为线段AB的包围盒。

对于第一种情况的杆件1，需要采用图形碰撞检测技术来进行识别，杆件和边界都视为线段，即判断线段与线段是否相交［11］。判断平面上两条线段AB和CD是否相交，可以先判断线段所在直线的交点是否在它们包围盒的内部。选取定义对角线的两个极值端点如图3所示，其交点可以通过以下方式计算。设AB 为L1（t）＝A＋t（B－A）；设CD为n·（X－C）＝0；其中n＝（D－C）⊥垂直于CD。通过联立上述方程可得t，而交点P＝L1（t）可以通过将t代入线段方程求得。判断P点是否在包围盒内只需判断0≤t≤1是否成立。判断AB和CD是否相交的准则是当P点位于其中一个包围盒外，则线段AB和CD 不相交，如图3（a）所示；当P点同时在AB和CD各自包围盒的内部，则AB和CD 是相交的，如图3（b）所示。通过上述方法即可将与凹边界相交的杆件移除。此外，两个端点都在凹边界上的杆件必定都在设计区域外，通过凹边界edge47和edge34上的节点序号，可以直接将bar37移除。不规则设计区域中如果形成孔洞，则需定义孔洞边界，与定义凹边界的方法相同。

图2 基于几何和网格生成满连接基结构Fig．2 Full level ground structure generation based on geometry and mesh

2．2．3 利用分区域生成基结构提升效率

当不规则设计区域的凹边界不包含曲线时，可以将其分割成若干个凸的子区域，以图2所示区域和网格都已划分的L型设计区域为例，步骤如图4所示。在进行杆件与边界的相交判断时，把子区域基结构从满连接基结构的杆件中暂时移除，会得到跨子区域节点间的杆件，其中包含了所有的区域外杆件。在此例中，最后只留有5个杆件，如图4步骤（3），在很大程度上减少了与边界判断相交的杆件个数，从而提升了效率。区域外杆件删除后得到的结果如图4步骤（5），再将子区域的基结构与留下的杆件集合，得到最终的基结构，如图4步骤（6）所示。

图3 线段AB和CD不相交和相交两种情况Fig．3 Two cases of un－intersection and intersection of line ABand CD

图4 分区域生成基结构Fig．4 Generate ground structure of subdomains

2．2．4 子区域的划分

对已知设计区域划分是本方法的第一步。对于实际问题中的一些特殊设计区域，针对各部分区域的特点，生成不同的有限单元网格。在凹边界没有曲线存在的情况下，可直接根据凹边界的性质将整个区域划分为最少数目的子区域，并保证子区域都是凸区域。而当凹边界中有曲线存在，则划分而成的子区域不可能全是凸区域，如果曲线边界由线段近似描述，在此基础上要划分较多的子区域才能保证皆为凸区域，增加了难度和复杂性。所以在此允许子凹区域的存在，并对其内部杆件增加一步判别和删除。以经典Michell梁问题中的不规则设计区域为例，具体实现步骤如图5所示。

首先划分两个子区域，如图5步骤（1）所示，粗实线是分割线，细实线是网格单元，左侧子区域为凹区域，右侧子区域为凸区域。图5步骤（2）为全局满连接基结构，杆件个数N＿all＝466，可以拆分为图5步骤（3）和步骤（4）所示的两个杆件集合，分别是各个子区域满连接基结构和跨子区域节点间的所有杆件。先得到各子区域基结构的集合，杆件个数分别为N＿sub1＝122和N＿sub2＝131，再将前者从满连接基结构中移除得到跨子区域节点间的所有杆件，杆件个数N＿left＝213。接下来仅对包含凹边界子区域的杆件（N＿sub1）和剩余杆件（N＿left）进行判别，即可将区域外的杆件移除，分别得到杆件如图5步骤（5）和步骤（6）所示，将两者合并得到了最终基结构如图5步骤（7）所示，所有杆件N＿final＝415都在设计区域内，符合要求。由于分区域的设定，其中子凸区域中的所有杆件（N＿sub2）不必参与判断的过程，在一定程度上提升了效率。

图5 分区域生成基结构（包含曲线凹边界）Fig．5 Ground structure of subdomains（with curve concave boundary）

2．2．5 二维问题基结构生成算例

图6给出了三种不同的设计区域，分别如图6所示方式划分子区域并构建网格。图6（a）是将L型设计区域的网格稍作细分；图6（b）是环形孔洞设计区域，具有不同的拓扑形式；图6（c）是存在两个曲线凹边界形状较为复杂的设计区域。可以看出，三种情况均在满连接基结构的基础上得到符合要求的基结构。

3 三维问题基结构的生成及算例

三维问题基结构的生成是二维基结构生成方法的延伸，不仅要提取节点、边界线段及平面单元，还要提取边界平面及立体单元的信息，其判断准则更为复杂，在此不详细叙述，提供三维L型算例以供参考。如图7所示，划分子区域且加深平面为凹边界平面，经过网格划分如图7（b）所示，生成满连接基结构如图7（c）所示，最后删除区域外部杆件，可以得到最终符合要求的基结构，如图7（d）所示。

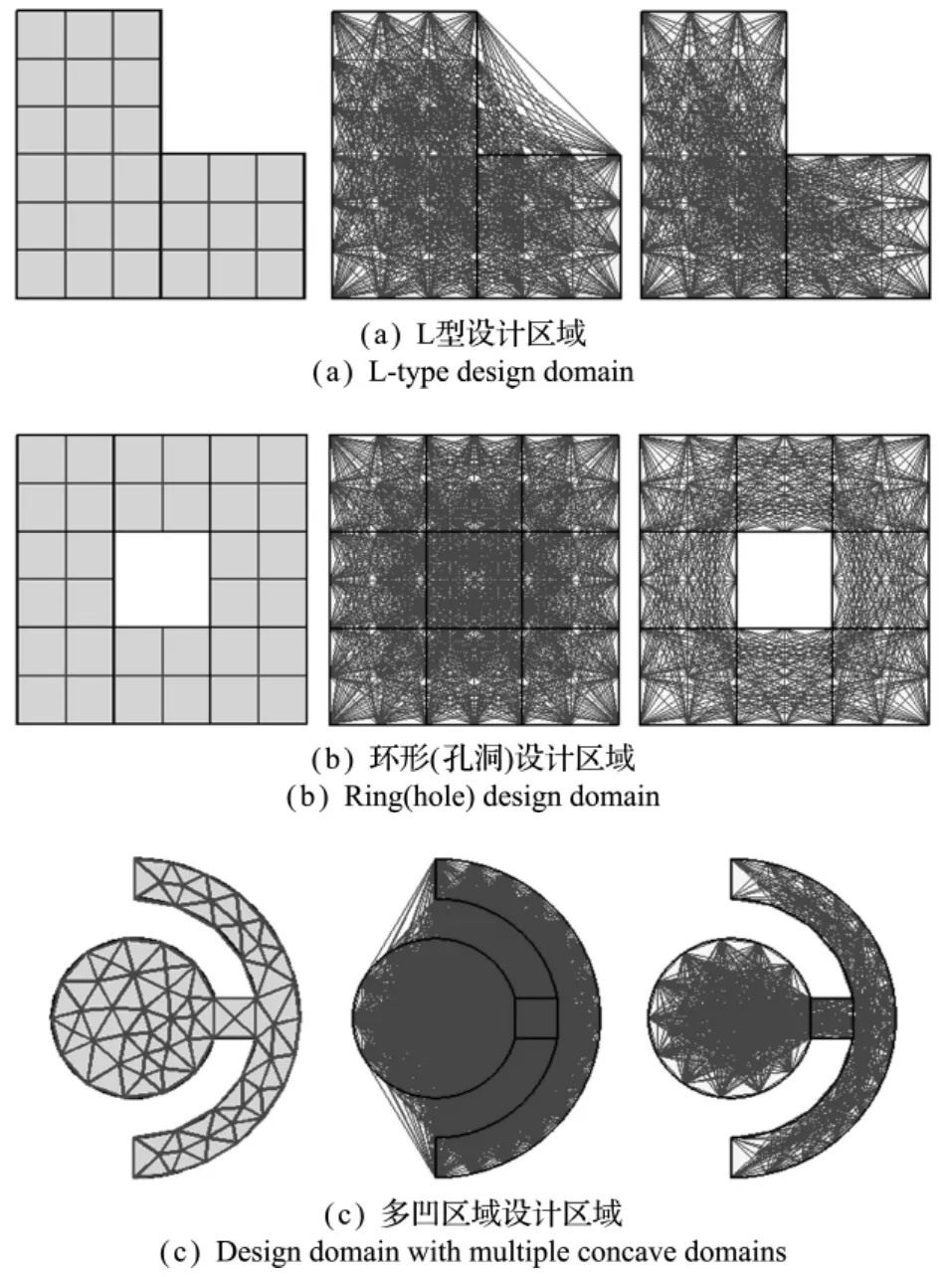
图6 不同设计区域基结构的生成Fig．6 Ground structure generation of different 2Ddomains

4 基于基结构法的桁架拓扑优化

4．1 基于塑性设计理论的拓扑优化模型

在单工况应力约束下，以最小体积为目标，以杆件横截面积为设计变量的桁架拓扑优化问题可表述为［12］

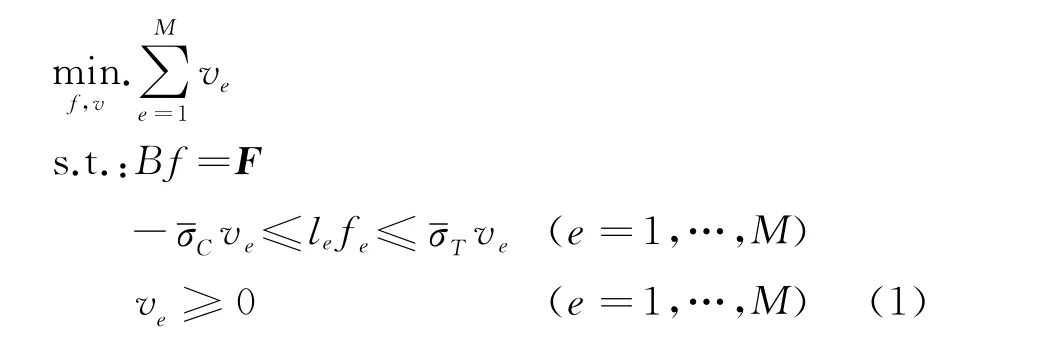
式中ve和fe分别为第e根杆件的体积和轴向载荷，M是杆件总数，F（N×1）为节点力向量，其中N为节点自由度。B（M×N）为柔度矩阵，其中第i行元素为 ［1，…，－Ca（xi），－Ca（yi），0，…，Cb（xi），Cb（yi），0，…］T。其中Cx和Cy分别为第i根杆从起点a到终点b的x和y方向上的余弦角。对于一个稳定的基结构，B具有满秩N（N≤m）和分别为拉压应力极限。

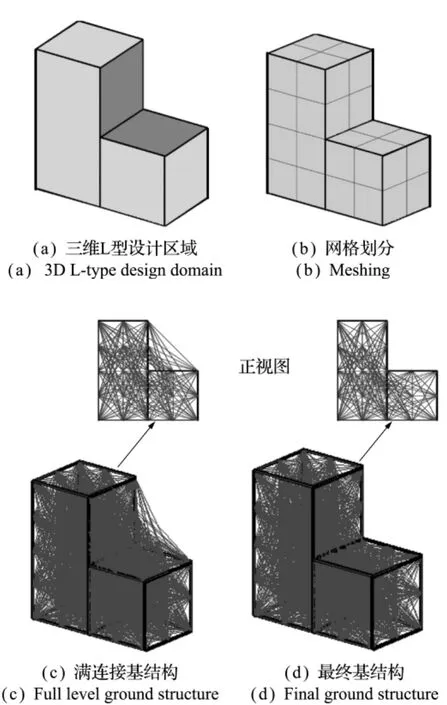
图7 三维问题基结构的生成Fig．7 Ground structure generation of 3Ddomain

为了满足满应力设计准则，将体积和载荷的表达式做如下的改动，

所以优化问题的公式可以转换成标准的线性规划问题：

式中f＋e和fe可分别视为第e根杆件的拉应力和压应力，至少一者为0，设计变量只有轴向载荷。如果fe＝0，f＋e＞0，则轴向载荷为拉；如果fe＞0，f＋e＝0，则轴向载荷为压；当fe＝0，f＋e＝0时，认为该杆件可以从基结构中删除。对线性规划问题，利用内点法可以很容易得到最优解。

4．2 基于基结构法的桁架拓扑优化算例

以经典Michell梁的桁架拓扑优化算例为参考。以图8（a）所示方式划分子区域并构建网格，黑色粗线为子区域界线，灰色细线为网格单元，共包含三角形单元Nt＝374和四边形单元Nq＝324（18×18），灰点表示约束施加点，箭头表示外加载荷。将横截面积截断值设置为cutoff＝0．018，在优化过程中用于约束杆件的横截面积，过滤掉过细的杆件，后续的算例中也会采用此截断值，可以有效地滤掉细杆又不影响最终的拓扑优化结果。其对应得到的优化结果如图8（b）所示。优化目标值为单位体积V＝4．367，迭代步数为Iter＝85。图9为 Michell梁理论的最优解［14，15］。

图8 经典Michell梁问题的基结构法拓扑优化结果Fig．8 Optimum topology from a ground structure implementation of Michell beam

同理，分别对环形（孔洞）算例、二维L型梁算例及三维L型梁算例进行优化，划分网格数分别为Nq＝144，Nq＝48及Nq＝192。其对应得到的优化结果（横截面积截断值cutoff＝0．018）分别如图10（b）、图11（b）及图12（b）所示。

图10算例网格数为Nq＝144，优化目标值V＝34．71，迭代步数Iter＝16。

图11算例网格数为Nq＝48，优化目标值V＝9，迭代步数Iter＝11。

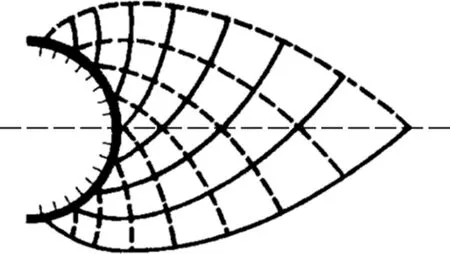
图9 经典Michell梁问题的理论最优结果Fig．9 Theoretical optimal solution of Michell beam

图10 环形（孔洞）问题的基结构法拓扑优化结果Fig．10 Optimum topology from a ground structure implementation of ring（hole）domain

图11 二维L型梁问题的基结构法拓扑优化结果Fig．11 Optimum topology from a ground structure implementation of 2DL－type beam

图12算例网格数为Nq＝192，优化目标值V＝9．59，迭代步数Iter＝19。

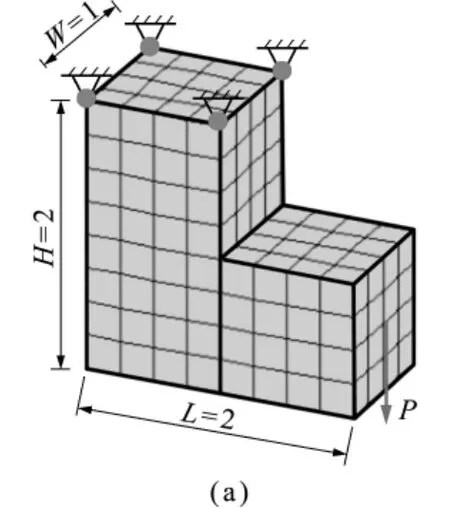
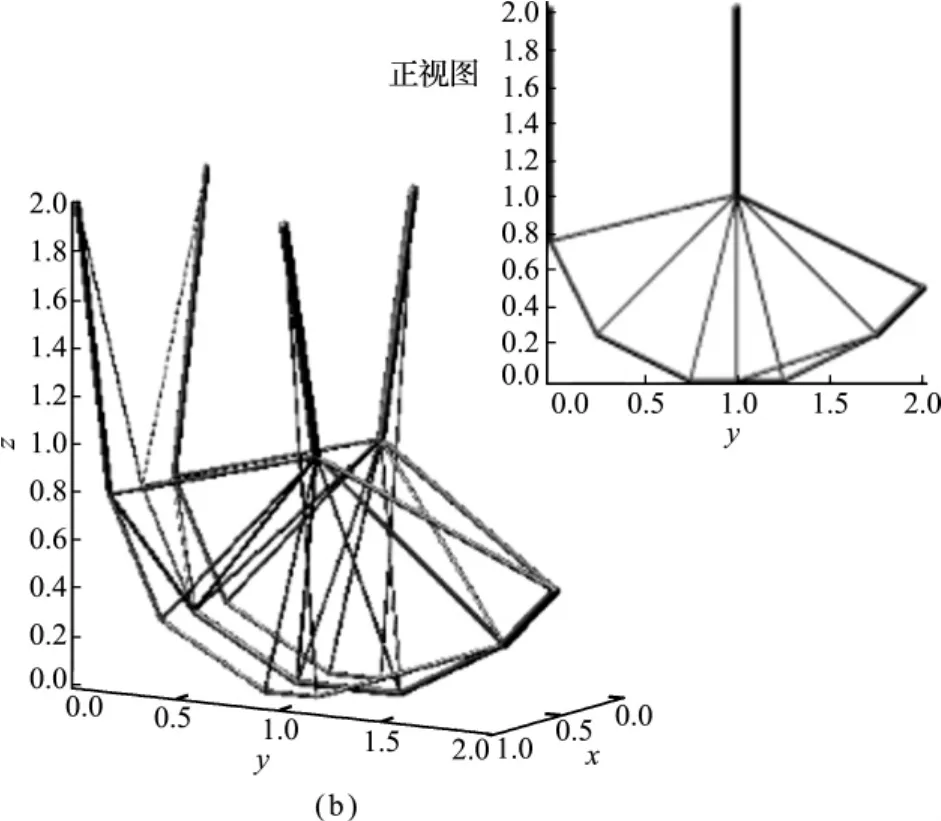
图12 三维L型梁问题的基结构法拓扑优化结果Fig．12 Optimum topology from a ground structureimplementation of 3DL－type beam

5 总 结

本文对在不规则设计区域内生成基结构的方法进行了探索和讨论。主要思想是在原始几何和网格基础上利用分区域生成基结构的方法，在非凸设计区域内迅速并准确地生成基结构。以非凸设计区域的凹边界为判断边界，可以快速准确地将位于设计区域外的杆件识别并删除。与传统的设置限制区域或者偏置区域的方法相比，避免二次建模，大大简化前处理过程，且避免受到限制区域（偏置区域）大小的限制，从而提高了所形成基结构的准确性。满足上述条件的最终基结构可以直接用于后续桁架的拓扑优化，并可以得到接近解析解的拓扑结构。故本文为基于基结构法的桁架拓扑优化提供了一种易实现且效率及准确度高的基结构生成方法。