一种新型控制方法—自抗扰控制技术及其工程应用综述
陈增强,刘俊杰,孙明玮
(1. 南开大学 计算机与控制工程学院,天津 300350; 2. 天津市智能机器人重点实验室,天津 300350)
PID控制是一种基于误差的反馈控制,其不依赖被控过程的模型,结构简单且鲁棒性强,至今仍在工程上占据着主要地位。而针对PID控制难以处理的复杂控制对象,现代控制理论产生并涌现了如最优控制、鲁棒控制、自适应控制等理论成果,大多数的现代控制理论方法均依赖于系统的数学模型,难以在实际应用中推广。1989年,韩京清[1]研究员就控制理论是“控制论”还是“模型论”展开研究讨论,强调若要解决鲁棒性问题,需要摆脱数学模型的束缚。此后,韩京清在研究出跟踪微分器 (tracking differentiator,TD)[2]、非线性状态误差反馈控制律(nonlinear state error feedback,NLSEF)[3]和扩张状态观测器(extended state observer,ESO)[4]之后,于1998年正式提出自抗扰控制 (active disturbance rejection control,ADRC)[5]。自抗扰控制的独特之处在于它将作用于被控对象的所有不确定因素均视为“未知扰动”,并利用对象的输入输出信息对其进行实时估计并给予补偿,这种思想突破了“绝对不变性原理”和“内模原理”的局限性,是在发扬PID控制的精髓—“基于误差来消除误差”,并吸收现代控制理论成就的基础上形成的一种新型实用控制技术。
自抗扰控制技术从提出到现在近20年,已有一些学者对自抗扰控制的发展、思想或理论成果进行了相关总结。韩京清研究员在文献[6]系统阐述了“从PID到ADRC”的发展,深入剖析了自抗扰控制的思想精髓;高志强[7-9]探讨了自抗扰控制思想的内涵和意义,并在文献[10]中从扰动抑制角度深入分析了自抗扰控制的优越性及发展趋势;黄一等[11]以自抗扰控制器的发展为线索,对其思想做了系统阐述,并在此基础上对自抗扰控制的思想、理论进展进行深入讨论与总结[12-15];王丽君等在文献[16]的基础上,概括了针对大时滞系统的自抗扰控制策略,并给出参数整定方法[17];夏元清等[18]概括了自抗扰控制和滑模控制的研究进展,并将二者结合提出了复合控制;陈文华等[19]在扰动观测器综述中,对扩张状态观测器进行了分析比较;Madoński等[20]对提高扩张状态观测器效率的方法进行了概括总结;李杰等[21]从自抗扰控制理论发展脉络的角度出发,系统地总结了自抗扰控制相关理论研究成果与进展;陈增强等[22]重点围绕近年来线性自抗扰控制理论的发展进行综述,并对线性自抗扰控制在实际应用中的典型案例进行总结。本文从工程角度出发,从自抗扰控制思想的提出、自抗扰控制技术的发展以及在实际工程中的应用各个方面对这种新型的实用化工程技术的发展脉络进行全面梳理,并对自抗扰控制技术的工程应用成果进行了系统的总结分析,在此基础上对自抗扰控制技术的发展趋势进行了展望。
1 自抗扰控制技术
1.1 自抗扰控制结构
自抗扰控制不依赖系统的精确模型,可直接利用被控对象的输入输出信息对系统状态以及“总扰动”进行估计并在线补偿,在存在多种不确定性时,依然可以保持良好的控制性能,其结构如图1所示,包括:跟踪微分器TD、非线性状态误差反馈控制律NLSEF、扩张状态观测器ESO及扰动补偿部分。
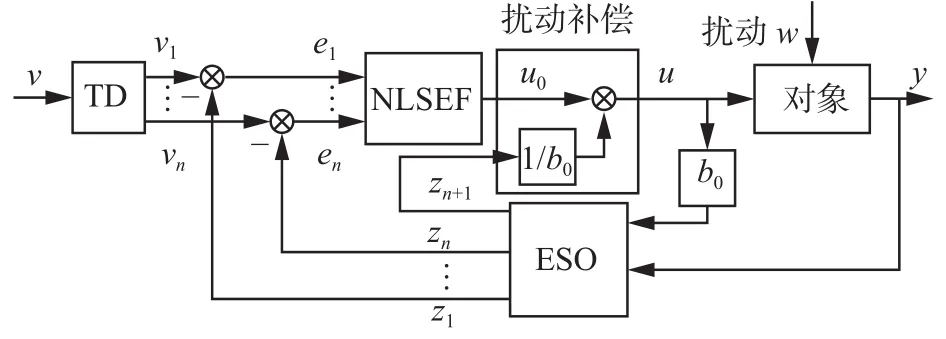
图1 自抗扰控制原理图Fig. 1 Principle map of ADRC
跟踪微分器能够快速地跟踪输入信号,并产生输入信号的近似微分信号,可分为非线性跟踪微分器和线性跟踪微分器。
将系统总扰动作为系统的新的扩张状态,针对扩张后的新系统设计状态观测器称为扩张状态观测器。扩张状态观测器对系统总扰动进行实时估计,扰动补偿部分根据估计出的总扰动进行合理补偿,可将原系统近似为积分串联型系统。
基于跟踪微分器和ESO产生的误差信号e1和各阶误差微分信号,可以选取不同的非线性误差反馈控制律。
1.2 线性自抗扰控制
最初的自抗扰控制中,ESO和NLSEF均含有非线性函数,使得理论分析具有很大难度,参数整定较为繁琐,不便于工程实际应用。针对原始非线性ADRC存在的不足,美国克利夫兰州立大学的高志强教授将非线性自抗扰控制器中的非线性环节线性化处理[23],并受韩京清研究员在文献[24]中所提时间尺度概念的启发,进一步提出频率尺度的概念,采用极点配置的思想将ADRC参数与频率联系起来,将可调参数简化为控制器带宽、扩张状态观测器带宽和扰动补偿增益3个参数,极大简化了ADRC的参数整定方法,推动了自抗扰控制的工程实际应用发展。
2 自抗扰控制理论发展
自抗扰控制理论领域中以线性自抗扰控制发展较为迅速,许多工程实际应用成果都是采用LADRC控制实现,下面以LADRC控制理论发展为主,适当结合传统ADRC的部分理论研究成果,对自抗扰控制的理论发展进行阐述。
2.1 参数整定与优化
针对非线性自抗扰控制的参数整定方法已有很多,文献[25]通过大量仿真研究了斐波那契数列与ESO参数的关系;文献[26]仍采用极点配置思想,此外,各类人工智能算法被用来对ADRC进行参数寻优,如粒子群算法[27]、人工免疫算法[28]、强化学习[29]、神经网络[30]及多目标优化[31]等。
高志强教授提出利用带宽确定线性自抗扰控制器参数后,许多文献针对带宽整定问题开展了相关研究。文献[32]在对非最小相位系统的LADRC进行研究时,在讨论系统高频增益和控制器带宽的基础上,给出参数整定过程;文献[33]从频域分析方法入手,基于LADRC控制器的闭环传递函数和频带特性曲线,系统地分析扩张状态观测器的估计能力和自抗扰控制器的稳定性,探讨系统动态特性与控制参数的关系,提出控制参数的工程配置方法。针对一阶惯性加延迟系统,文献[34]将LADRC转化为内模控制结构,导出了其中控制器、滤波器、乘性不确定性、互补灵敏度系数函数的对应表达式,分析了扩张状态观测器的参数对闭环稳定性的影响,并总结出扩张状态观测器的两条参数整定准则;而文献[35]将LADRC转化为二自由度内模控制结构,将LADRC的带宽整定等价为内模控制中设定点滤波器和扰动抑制滤波器的两个时间常数的整定。薛文超分别在一定采样率下和采样率不快的情况下,研究了一类非线性系统自抗扰控制的参数整定问题,利用理论分析指出采样率,自抗扰控制器参数,系统不确定性大小以及闭环系统特性之间的关系[36-37]。文献[38]针对线性自抗扰控制器参数整定问题,提出一种基于动态响应过程时序数据挖掘的参数自整定算法,并在液压位置控制系统上测试,是一种具有实用性的线性自抗扰控制器参数自整定方法。
2.2 ADRC性能分析
1) 收敛性与稳定性
对于非线性TD的收敛性,郭宝珠等[39]在一定条件下,给出了非线性TD的收敛性的严格证明。文献[40]提出一种简单的线性TD,并证明了带有随机扰动的任意可微输入信号的收敛性。文献[41]基于奇异摄动理论提出一种有限时间收敛的线性TD。针对一种三阶线性TD,文献[42]从连续和离散两个方面证明其收敛性。
D.Yoo等[43]在假设系统动态及其导数有界的情况下,研究了LESO对状态的估计性能和收敛性,并进一步对离散ESO的收敛性进行分析证明[44];在文献[43]的基础上,文献[45]将假设条件放宽,即在系统动态有界或其导数有界情况下,证明了LESO估计误差有界;文献[46]推导了含有不确定性的n阶单入单出非线性系统离散扩张状态观测器的误差方程,通过归纳法证明了该扩张状态观测器的收敛性。
Zheng等[47]分析了具有不确定性的非线性时变系统的LADRC的稳定性,当系统模型动态完全已知时,系统为渐近稳定;当存在模型不确定性时,ESO估计误差和控制器跟踪误差均有上界,且随着带宽增加而单调递减。在此基础上,文献[48]针对多入多出系统,证明了在扩张状态观测器跟踪误差趋于零的前提下,LADRC闭环系统是输入–输出有界稳定的;文献[49]针对不确定线性时不变对象,推导了LADRC控制器的传递函数,并利用频域方法分析系统的性能及稳定性;文献[50]则研究了带有时变的非线性动态和不连续外部扰动的不确定系统的自抗扰控制,在明显弱化了不确定性假设的情况下,定量分析ESO带宽和闭环系统性能之间的关系,并给出系统指数稳定的条件;文献[51]从时域和频域的联系角度对自抗扰控制进行研究,ESO和ADRC的稳定性可以通过解微分方程的方式代替李雅普诺夫方法进行分析,进一步揭示了误差界和ADRC带宽的关系。奇异摄动理论被用来对ADRC稳定性进行分析,如文献[52]采用奇异摄动理论研究了带有未知模型动态的非线性时变系统的LADRC的闭环稳定性,将闭环误差动态系统转化为奇异摄动系统,基于复合李雅普诺夫函数方法证明了观测器误差充分小时闭环系统是指数稳定的;近年来,关于ADRC的稳定性分析又有新的进展,在文献[52]的基础上,文献[53]基于奇异值摄动理论,将闭环误差动态准解耦为相对慢的子系统和相对快的子系统,分别对应反馈回路和扩张状态观测器,数学分析表明当观测器初始误差充分小时,系统存在独特的指数解,推导系统渐近解的过程揭示了ADRC的稳定性条件以及扰动变化率与估计误差大小的关系,指出总扰动的可微是唯一需要进行的假设。而文献[54]则指出,由于在实际应用中存在非线性、不确定性以及扰动等问题,进行定量的鲁棒稳定性分析是很有必要的,并针对基于自抗扰控制的单入单出系统,将其转化为摄动间接Lurie系统,在总扰动满足线性增长约束的假设下,利用Popov-Lyapunov方法研究其全局和局部稳定性,在控制器设计过程中,已建模的线性动态容易被集成到自抗扰控制中,提高了动态性能和稳定性能;所提方法能适用于基于线性自抗扰控制和非线性自抗扰控制的系统,以及其他可以转换为摄动间接Lurie系统,并推导出控制器所能容忍的总扰动的鲁棒稳定界。
2) ADRC其他性能分析
ESO是自抗扰控制器的核心部分,其任务是根据输入输出数据观测系统的状态和总扰动。文献[45]分析了LESO估计不确定性的能力,给出能被ESO观测并具有有界观测误差的扰动范围,并对几种典型不确定扰动的观测误差进行分析;文献[55]严格证明了一类具有不确定性的非线性系统的ESO的收敛性,并针对系统内部不确定性和外部随机干扰分析了ESO的估计能力。对于带有不确定性的n阶系统,文献[56]证明了ESO估计误差有上界,并随着带宽增加,估计误差单减,在模型动态完全已知时,估计误差趋于零,指出ESO能够用于一大类具有不确定的时变非线性系统的扰动估计;文献[57]探讨了高阶及传统LESO的动态响应、干扰抑制能力与观测器参数间的关系,在估计能力、峰值现象的抑制、滤噪性能等方面对传统LESO进行了性能评估与仿真验证;针对典型一阶惯性环节,文献[58] 在输入时延敏感的情况下研究了ESO带宽选择不当造成系统失稳的现象,并定量分析了ESO带宽、控制器参数和输入时延容忍度之间的关系,使得参数整定能够兼具到ESO的观测精度与控制系统的鲁棒性能。
系统的频域分析更容易被工程师理解接受,文献[59]针对运动控制中位置扰动和力矩扰动问题,首次通过频域响应分析,验证了在干扰抑制方面ADRC较PID有更好的效果;田刚等[49]针对不确定线性时不变对象,首次推导了LADRC控制器的传递函数,利用频域方法分析系统的性能和稳定性;文献[60-61]针对具有不确定性的单入单出线性定常系统的LADRC,给出一种估计系统截止频率和相位裕度的方法,并指出各参数对截止频率和相位裕度的影响;文献[62]在解决飞行器的姿态跟踪及干扰抑制问题时,基于频域理论,着重分析了LESO阶次对系统性能的影响。2016年,Zheng等[51]在自抗扰控制快速发展的背景下,以工程师熟悉的频域响应的语言方式对其作出解释,并再次强调关键的带宽概念,指出这一概念可以作为自抗扰控制状态空间表达和实际工程师关心的指令设计间的纽带,文中在频域和时域分别对自抗扰控制进行了分析,通过解微分方程这种更为直接的方式,建立了跟踪误差与自抗扰控制带宽之间的联系,便于工程师理解,并表明如果系统部分模型信息已知,且被集成到ESO中,可以提高系统性能,降低噪声敏感,同时减少系统带宽。
2.3 ADRC在处理特定系统中的应用
自抗扰控制能够处理的系统呈现多样化,具有很好的应用前景,利用自抗扰控制思想解决各类特定控制系统的控制问题,具有重要的理论与实际意义。本文介绍几类特定系统的自抗扰控制思路或方案:
1) 非最小相位系统
非最小相位系统是指传递函数中含有正实部零点的系统,其特点是阶跃响应会出现负调,严重影响系统的快速性与稳定性。文献[63]通过实例仿真说明ADRC可以用于不稳定对象和非最小相位系统的控制。此后,文献[64]则研究了LADRC用于非最小相位系统控制的具体方法,并在讨论系统高频增益和控制器带宽关系的基础上,给出整定过程。文献[65]则采用状态空间分解方法,将不确定非最小相位系统分解为控制通道和输出通道,针对由能控标准型构成的控制通道,使用ESO观测包括模型偏差在内的系统总扰动;针对含有正实部零点的输出通道设计前馈控制器,最后给出稳定性证明。在此基础上,文献[66]对具有模型不确定性和外部扰动的非最小相位系统,将LADRC中的串联积分器用标称系统的能观标准型替代,并基于频域理论分析了系统的稳定性。
2) 大时滞系统
化工、冶金、石油等流程工业系统中均含有时滞现象,针对大时滞系统的控制问题,韩京清研究员给出几种解决思路[67-68],包括无视时滞法、提高阶次法、输出超前法和输入超前法。以上思路均适用于ADRC与LADRC控制,且都是将时滞对象近似或变换为无时滞对象后,进而设计自抗扰控制器,其中输出超前法和输入超前法要求系统时滞较精确已知。在此基础上,王丽君等[17]进一步概括了时滞系统的自抗扰控制方法,并介绍了ADRC输入时滞法的使用,该方法直接针对时滞对象设计相应的延时ESO,突破了之前方法的限制。
3) 多变量系统
文献[69]针对多变量耦合系统,基于线性自抗扰控制提出一种动态扰动解耦控制策略,采用主动估计和补偿措施消除控制对象的内部动态和外扰,实现具有未知动态的多变量系统的解耦控制,并在精馏塔和连续搅拌反应器两种典型化工装置上进行仿真验证。薛文超等[70-71]将LAD-RC用于带有不确定和扰动的一类多输入多输出下三角系统的控制,获得了期望的控制性能。
4) 分数阶系统
文献[72]基于ADRC将分数阶系统中的分数阶动态视作扰动,针对分数阶系统提出一种整数阶控制结构,并对系统的稳定性进行分析。文献[73]研究了非线性分数阶系统的ADRC控制,首先通过研究分数阶最优控制结构,利用Hamilton函数和分数阶最优条件提出分数阶跟踪微分器;其次,设计了线性分数阶ESO对非线性函数和非线性分数阶对象中的扰动进行估计,最后利用该估计值,通过补偿措施,将非线性分数阶控制对象转化为线性分数阶对象。
5) 混沌系统
针对一类连续时间异结构混沌系统,文献[28]提出了一种异结构混沌系统反同步的自抗扰控制策略。对于统一混沌系统,文献[74]采用自抗扰控制实现了对混沌系统的有效控制,并分析了闭环系统的稳定性。文献[75]将ADRC-GPC算法应用于混沌系统的同步与控制,表明该算法可直接用于非线性系统的控制器设计。
6) 非线性非仿射系统
程春华等[76-77]针对一类具有外部扰动的不确定非仿射纯反馈非线性系统,结合反演和自抗扰技术,提出了一种新的控制设计方案,该方案中反演设计的每一步引入了自抗扰设计,同时采用微分器和扩展状态观测器分别估计虚拟控制的导数和系统的未知部分,并且通过输入状态稳定性分析证明了系统状态能渐近收敛到原点的任意小邻域内,仿真结果证实了该方法的有效性。
2.4 ADRC的一些改进方法
1) ESO改进
自抗扰控制中ESO的作用尤为重要,吸引了大量研究人员对其进行分析改进。文献[78]提出降阶观测器,减少了相位滞后,且使得参数更容易整定;文献[79]提出一种基于超扭曲算法的滑模扩张状态观测器,使得观测误差在有限时间收敛到零,且适用于控制增益b不为常数的情况;受ESO提出的启发,文献[80]针对一类带有连续不确定动态和离散测量噪声的多入多出非线性系统,提出一种新型滤波器—扩张状态滤波器(ESF);文献[81]和文献[82]均基于ESO提出自适应扩张状态观测器(AESO),能够自动实时整定并减少状态和总扰动的估计误差;文献[83]给出一种有限时间收敛的ESO,与传统ESO相比,其不将未知总不确定性的一阶时间导数视作零处理,适用于高精度要求的控制系统,仿真和实验证明了该扩张状态观测器的有效性;文献[84]研究了一类具有非线性未知动态和外部扰动的传感器延迟系统的控制问题,在自抗扰控制的基础上提出扩张状态预测观测器,该方法在有传感器延迟的情况下,能够实时估计和补偿系统总扰动;文献[85]针对高增益扩张状态观测器初始时刻出现较大峰值的问题,指出采用时变增益在很大程度上可以减小其峰值;文献[86]针对含有交叉耦合、参数不确定性和外部扰动的两入两出系统,基于LADRC提出一种改进的降阶观测器,在多变量水箱控制系统上的实验验证了该方法的有效性。
2) 与其他方法结合
针对一些特殊系统或特殊环境的对象,单一的自抗扰控制可能不是最优的控制方案,许多学者将其他方法引入进来,与自抗扰控制结合起来,进一步提高控制效果。文献[87]提出滑模控制与自抗扰控制结合的复合控制策略,以克服滑模控制的抖振问题和自抗扰的估计能力受限问题。赵申等[88]在解决带有右半平面零点和时延的非最小相位系统的控制问题时,将线性自抗扰控制与一种前馈控制相结合,以克服带宽限制问题。文献[88-89]针对时滞对象的控制问题,提出预测控制和自抗扰控制结合的控制策略。文献[90]将自抗扰控制与广义预测控制有机结合起来,提出一种新型自抗扰广义预测控制器,该算法可直接用于非线性被控对象的控制设计。文献[91]在研究死区不确定性和扰动抑制问题时,将传统史密斯预估器和自抗扰控制结合,以处理由PI控制器的相位滞后引起的振荡。Pan等[92-93]对倒立摆系统在任意平衡点线性化的基础上进行微分参数化,将欠驱动系统解耦为两个较低阶的系统,提出一种微分平坦和自抗扰控制相结合的控制策略,与未考虑解耦性的基于自抗扰控制的观测器相比,具有更好的跟踪性能。文献[94]针对二自由度双电机多输入多输出系统,提出一种基于自抗扰控制和输入成型的复合控制,其中,自抗扰控制用来处理未测量动态、模型不确定性以及未知扰动力矩,输入成型旨在提高动态性能,这种控制策略不必将原系统划分为水平和垂直子系统,该控制器的动作允许系统在非线性和复杂耦合条件下,具有良好的定点跟踪行为和较强的干扰抑制效果,实验结果表明,该复合控制策略对系统参数的变化,如自然频率和阻尼比,具有很强的鲁棒性能。
3 自抗扰控制的实际应用
自抗扰控制不依赖于系统的数学模型,抗干扰能力强,LADRC不仅具有这种优势,而且结构简单,参数易于整定,在工业过程、伺服系统控制、汽车发动机控制、航空航天等各个领域都进行了成功的应用,具有很好的工程应用前景。下面列举一些自抗扰控制的实际应用进行说明。
3.1 工业过程
1) 塑料挤压机生产线
高志强团队[95]成功将LADRC技术应用于美国Parker公司的挤压机生产线,被控量为挤压机的桶区温度,控制量为加热开关的占空比,与PID控制相比,具有良好的控制精度和动态性能,而且节能效果显著,达到平均节能57%。
2) 精馏塔等气体流量装置
郑青等[69]以精馏塔等多变量耦合系统为例,基于LADRC提出一种动态扰动解耦控制策略,通过主动估计和补偿消除内部和外部扰动,能够实现带有未知动态的多变量系统的解耦控制;文献[96]针对多变量系统存在耦合性的特点,对解耦后的时滞子系统设计了自抗扰控制器,以精馏塔模型为例,验证了算法的有效性;文献[97]针对气体流量装置系统,利用自抗扰控制实现解耦控制,与PID相比,解耦效果更好,对扰动抑制效果更优,鲁棒性更强。
3) 大型热处理电阻炉
胡彬等[98]针对电阻炉具有大的惯性、延迟、系统外界带来的不确定性干扰和模型参数时变等特点,提出一种在工厂实用的线性降阶自抗扰控制及快速参数确定策略,与常规的PID控制相比,耗电量降低20%,控制精度提高25%以上。
4) 大型发电机换热器
清华大学李东海团队针对1 000 MW大型火力发电机换热器工作过程中存在的多种干扰及时滞问题,以冷凝液位高度为被控量,设计了线性自抗扰控制器,在实际控制中取得良好效果,并实现ADRC与PID控制器的无扰切换[99-100]。
3.2 伺服系统
1) 快速刀具伺服系统
清华大学吴丹团队为解决FTS的快速精密跟踪控制问题,根据刀具运动参考轨迹已知的特点,应用自抗扰控制原理和前馈控制策略,分别设计了采用线性和非线性扩张状态观测器的自抗扰控制器。该控制策略已应用于发动机活塞的精密非圆车削和二维正弦微结构表面的超精密车削[101-102]。
2) 液压伺服系统
王喆等[103]针对轧机传动侧和操作侧液压伺服位置系统存在不一致性而引起两侧位置不同步的问题,从工程应用角度出发,提出一种自抗扰同步控制方法,并在某400 m可逆冷带轧机液压伺服位置系统中进行验证;Wang等[104]通过引入奇异摄动理论,原始双动态模型降为积分链系统,针对该系统设计自抗扰控制器,并在液压伺服系统实验平台上进行实验测试。
3) 永磁同步电机
滕青芳等[105]针对永磁同步电机系统,提出了基于自抗扰控制的直接转矩控制策略,与基于PI的DTC策略相比,具有更强的抗负载干扰能力和跟踪给定转速变化的能力;Li等[106]针对直接驱动永磁同步电机的风能转换统,在设计自抗扰控制器时,将可用模型信息合并到扩张状态观测器使得总扰动补偿效率更高。
4) 大型测控天线伺服系统
邱德敏等[107]为了改善风载荷干扰对深空探测天线跟踪精度和寿命的影响,设计了位置环线性自抗扰控制器,深空探测系统上的应用结果显示,提出的控制策略超调比原产品减少了34%,抗击阵风干扰能力提高了60%,跟踪精度提高显著。
3.3 汽车发动机
天津大学谢辉团队针对汽车发动机对运行工况的高度敏感性及易受干扰等问题,将LADRC与基于模型的前馈控制以及解耦控制结合起来,提出一种汽车发动机的控制策略,并分别应用于均质压燃点火系统(HCCI)[108]、废气再循环系统(EGR)和可变几何涡轮增压器系统(VGT)[109]、发动机电动液压可变气门正时系统[109],并在不同负载和转速的情况下验证所提方法的有效性和鲁棒性。
3.4 飞行器控制
孙明玮等[110]应用LADRC处理飞行器的俯仰和横滚姿态控制,仿真及部分硬件测试结果表明自抗扰控制的动态性能和鲁棒性均优于PD控制;方勇纯等[111]针对无人直升机系统航向通道扰动大等问题,设计了一种自抗扰控制算法来实现其高性能控制;陶金等[112]针对翼伞系统在较大风场中难以准确跟踪归航轨迹、实现精确着陆的问题,设计自抗扰控制器进行修正,提高抗风性能和归航精度。
3.5 导弹飞行制导
孙明玮等[113]针对飞行控制系统实验转台中无刷直流伺服系统的摩擦补偿问题,提出一种基于指令补偿的无摩擦模型低速补偿策略,避免对摩擦模型和速度信息的依赖;肖增博等[114]针对导弹制导系统中存在的模型不确定性和外部扰动,通过为俯仰和偏航回路分别引入自抗扰控制,实现了双回路的动态解耦。
3.6 倒立摆控制
M. Ramirez-Neria等[115-116]将线性自抗扰应用于旋转倒立摆和惯性轮倒立摆的控制,自抗扰控制器能够实时估计通常由于线性化而忽略的高阶非线性,并通过实验结果验证方法的有效性;聂卓赟等[117]将倒立摆系统中存在的周期扰动、模型不确定性和间隙迟滞非线性等效为控制系统的输入端扰动,基于此设计自抗扰控制器以实现复杂环境下倒立摆系统的摆角控制。
3.7 机器人控制
Nadhynee等[118]研究了双足机器人的扰动估计和鲁棒控制问题,基于高增益扩张状态观测器设计了鲁棒控制器以实现扰动估计和补偿; Yi Long等[119]将自抗扰控制应用于下肢外骨骼康复的人类步态跟踪控制,实验结果表明采用的自抗扰控制方法与传统PID控制相比具有更好的控制性能。
3.8 电力系统负荷控制
谭文等[120]通过研究负荷频率控制系统的线性自抗扰控制,针对负荷频率控制中存在的发电速率约束的问题,将汽轮机理论输出与实际输出误差作为扰动输入,利用LADRC估计并快速补偿该误差,达到抗积分饱和的作用,并将该方法推广到具有再热汽轮机和水轮机系统以及多区域电力系统。
3.9 DC-DC功率转换器
Sun Bosheng等[121]针对1 kW桥式直流–直流功率转换器中存在的强非线性和外部扰动问题,利用自抗扰控制技术设计控制器,建立基于带宽参数化和扰动量化技术的参数整定方法,并在硬件平台上进行算法实现,结果表明当负载电流发生变化时,自抗扰控制器具有很好的扰动抑制能力;李世华等[122]将ESO和滑模控制结合,针对功率转换器中的不匹配扰动问题,设计控制器,并进行严格的稳定性分析,实验结果表明所提出的控制方法较传统滑模控制具有更优良的性能。
4 总结与展望
韩京清研究员最早提出的非线性ADRC由于需要整定的参数太多,制约了ADRC在实际工程领域推广应用。在此基础上,高志强教授对非线性环节进行线性化,减少控制器参数,并与带宽相联系,极大地推进了自抗扰控制的实际应用。本文就自抗扰控制理论发展及实际应用进行了较为系统的整理介绍,目前,自抗扰控制的理论研究与实际应用均取得了很大进展,每年均有各类成果不断涌现,并仍在不断丰富与完善中,展望未来的研究方向,可以从以下几个方面进行分析研究。
1)系统带宽受限问题
ESO作为自抗扰控制器的核心部分,对扰动估计要求越精确,需要的观测器带宽越高,而高带宽会使得观测器对噪声敏感;在实际应用中,系统的带宽也会受到一些物理限制,所以研究如何在带宽受限情况下达到最好的观测效果,具有一定的理论意义和实际价值。
2)与其他控制方法结合
针对一些特殊系统或特殊环境的对象,单一的自抗扰控制可能不是最优的控制方案,可以借鉴其他控制方法的研究成果,进一步提高控制效果。
3)信息获取
自抗扰控制不依赖模型,但是仍需对被控对象有一定的了解,如一般需要知道被控对象的阶次、输入输出通道个数和联结方式、信号延迟时间等信息,对于一些复杂的模型,如何获取自抗扰控制所需要的基本信息,仍然值得研究。
4)由单一结构向统一融合的主动抗扰结构过渡
可以将其他主动抗扰技术(包括Disturbance observer DOB,Perturbation Observer POB等)纳入进来,向统一融合的主动抗扰框架发展,这是未来自抗扰控制的发展趋势。
5)实际应用推广
自抗扰控制已经应用于部分实际系统,推广应用仍需加强,针对各类实际工程完成自抗扰控制的产品化实现,充分发挥自抗扰控制的优势作用。

