月地高速再入返回器气动辨识数据偏差分析

王贵东, 李 齐, 王 超

(1. 中国航天空气动力技术研究院, 北京 100074; 2. 中国空间技术研究院, 北京 100094)

0 引 言

返回器再入过程中具有大空域、宽速域的特点，准确预测其气动力特性十分困难，必须综合利用理论计算、风洞实验、飞行试验等多种手段。无论哪一种气动预测手段，得到的气动数据都不可能绝对准确，都有一定的偏差。因此，气动偏差分析是空气动力学研究的重要课题。

月地高速再入返回飞行以11 km/s左右的高速半弹道跳跃式再入大气层，在我国航天领域尚属首次[1]。与“神舟”飞船相比，气动环境及气动设计要求都具有新的特点。对于第二宇宙速度跳跃式返回，美国、前苏联分别研制了阿波罗系列[2]、探测器系列[3]等月地探测飞船，并进行了多次飞行试验。

从返回器飞行试验数据中辨识得到的气动力数据，是评估返回器气动性能的最具权威最有说服力的结果，也是评价地面气动预测数据，改进气动预测技术的重要依据[4]。五十年前，在航天测量技术远不如今天的条件下，美国利用阿波罗飞船飞行试验测量数据，通过气动辨识获得了配平迎角、升阻力系数、升阻比等关键气动力参数[5-10]。我国“神舟”飞船也针对气动辨识开展了试验设计和气动辨识方法研究，并对多次飞行试验数据进行了气动辨识，获得了包括喷流力矩在内的关键气动力参数[11-13]。

同样，飞行试验气动辨识结果也存在偏差，为了更有效地应用气动辨识结果，需要同时给出气动辨识数据的偏差区间。返回器气动辨识数据的偏差取决于试验方案、辨识方法、测量误差等多个因素，其中测量误差是产生气动辨识数据偏差的最主要的因素[14]。本文主要研究返回器气动辨识方法，以及基于测量误差的气动偏差分析方法，即从返回器气动辨识数学模型出发，根据观测参数的测量误差，计算气动辨识数据的偏差。

关于气动参数辨识数据的偏差分析问题，一直受到飞行器设计部门和研究人员的高度重视，并开展了大量的研究工作，研究方法主要有多次飞行试验数据统计方法、单次飞行试验置信区间估计方法等。多次飞行试验统计分析方法是一个十分有效的方法，但需要一定数量的飞行数据样本，这在应用中受到了限制。单次飞行试验的置信区间估计方法利用克拉马-罗界，结合置信度得到测量噪声产生的数据偏差区间，但实践中克拉马-罗界存在量值偏小的问题，文献[14]提出的修正方法较好地解决了该问题。本文将该方法应用到返回器气动力矩导数、喷流推力等参数辨识偏差的确定。

对于沿弹道的配平迎角、气动力系数、升阻比等时序气动参数的偏差估计问题，本文从上述参数的求解公式出发，采用基于测量误差的蒙特卡洛误差分析方法，本方法可以解决单次飞行试验条件下，沿弹道的时序气动参数的偏差的估计问题。首先，建立返回器气动力参数辨识的数学模型，包括配平迎角、升阻比、气动力系数等。进而，分析影响辨识结果的主要测量误差因素，为偏差分析提供依据。最后，采用蒙特卡洛分析方法，在假定测量误差为均匀分布的条件下，计算各种测量误差产生的气动力参数估计偏差，并利用统计分析方法，得到偏差的样本标准差和最大偏差区间，为气动数据的飞行试验与地面设计对比分析提供依据。

1 气动参数估计方法

气动参数估计是指利用飞行试验测量数据提取气动力参数，也是气动参数辨识的关键步骤。在进行气动参数估计之前，需要进行数据预处理和数据重建，以减小或消除试验数据的误差和噪声，提高气动参数估计的精准度。

1.1 数据预处理与重建

返回器系统本身及飞行环境条件的复杂性，传感器和数据采集系统的非理想性等众多因素的影响，不可避免地使飞行实测数据中含有确定性误差和随机误差。因此在将飞行试验数据用于气动参数辨识之前，应首先对试验数据进行各种预处理，以尽可能地消除各种确定性误差和随机误差。数据预处理包括采样时刻校正、异常值的判断、插值加密、数字滤波、微分平滑、传感器安装位置校正、坐标转换等。

数据预处理后，还需要对惯性测量数据和GPS测量数据进行相容性分析与数据重建。在返回器再入飞行试验中，利用惯性系统获得的加速度、角速率和姿态四元数等数据，以及利用GPS系统获得的轨道坐标、飞行速度等数据是进行飞行器设计、改进和定型最具有说服力的依据。然而，由于飞行实测数据中含有确定性误差和随机误差，造成两种测量数据不相容。另外，轨道数据采样频率较低，且存在大范围的数据缺失。通过数据重建，可以估计并修正加速度、角速率、姿态角等数据的误差，重建由于通信中断而缺失的轨道数据，获取完整的再入段轨道数据。轨道重建的基本步骤为：

(1) 分析飞行试验测量系统的误差因素，建立惯性测量数据、GPS测量数据的误差数学模型；

(2) 建立描述惯性测量参数与GPS测量参数之间关系的动力学和运动学状态方程组；

(3) 估计误差模型中的未知参数，目标是积分预测轨道与GPS测量轨道最大程度的相容；

(4) 利用估计得到的误差模型，修正内测数据的系统误差和轨道初值误差；

(5) 根据运动学方程组，积分得到返回器再入轨道。

图1给出了重建轨道随时间变化历程，从左至右分别为高度、经度、纬度。可见，没有外测数据的“黑障区”轨道得到了重建，并且重建轨道与测量轨道具有很好的一致性。辨识得到的过载和角速率常值测量误差都很小，在合理的范围内。由于该轨道重建方法综合利用了惯性测量数据和GPS测量数据，并考虑了地球曲率和自转，因此得到的重建轨道具有很高的可靠性，可以作为气动参数估计和飞行性能分析的依据。

(a) 高度

(b) 经度

(c) 纬度

1.2 气动力参数估计

经过数据预处理和轨道重建，不仅修正了加速度和角速率的常值误差和随机误差，而且重建了姿态角、速度和坐标等数据。数据重建后，各参数之间具有很好的相容性，可以根据动力学方程和几何关系，直接估计迎角、气动力系数和气动力矩系数等参数。

首先根据大气测量数据，将当地风速转换到返回坐标系。然后求返回器与大气的相对速度，并将相对速度转换到体轴坐标系。则迎角侧滑角的计算公式为

α=arctan(-Vyb/Vxb)(1)

β=arcsin(Vzb/V)(2)

其中，Vxb、Vyb、Vzb为相对速度的体轴系分量；V为总速度；α、β为迎角和侧滑角。配平迎角αT根据迎角的时间历程，利用数据平滑方法得到。

在已知加速度、喷流推力、动压等参数的条件下，气动力系数的计算公式为

Cx=(max-Tx)/(qS)(4)

Cy=(may-Ty)/(qS)(5)

Cz=(maz-Tz)/(qS)(6)

CL=Cycosα+Cxsinα(7)

CD=Cysinαcosβ-Cxcosαcosβ-Czsinβ(8)

CLD=CL/CD(9)

其中，Tx、Ty、Tz为喷流推力体轴系分量；q=ρV2/2为动压；ρ为大气密度，采用国军标大气密度模型。

图2和图3给出了配平迎角和升阻比估计结果

图2 配平迎角飞行试验与CFD结果对比Fig.2 Trim angle of flight test compare with CFD

图3 升阻比飞行试验与CFD结果对比Fig.3 Lift-drag ratio of flight test compare with CFD

与地面预测结果对比，可见飞行试验结果与地面CFD预测结果比较一致。

2 气动力矩参数估计

气动力矩参数估计采用基于极大似然估计的输出误差方法，泛函极值的求解采用修正牛顿-拉夫逊方法。下面给出参数估计的数学模型[15-16]。

2.1 状态方程

状态方程为绕质心运动的动力学方程组，高度和速度为缓变量，直接采用重建后的轨道数据。

qSL[Cmx,Cmy,Cmz]T-ω×(MIω)(10)

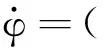
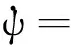
式中，ωx、ωy、ωz为角速率体轴系分量；φ、ψ、γ分别为俯仰角、偏航角和滚转角；Mjx、Mjy、Mjz为喷流力矩体轴系分量；MI为转动惯量矩阵。

2.2 观测方程

观测量取角速率和姿态角，观测方程为

式中，下标“m”表示测量值；εi(i=1,2,…,6)为零均值随机噪声。

2.3 估计参数

3 气动偏差分析

气动数据偏差主要取决于测量参数的误差。首先分析影响气动辨识结果的误差因素，及具体的测量精度。在此基础上，根据式(1)～式(11)所述的气动参数估计模型，利用蒙特卡洛分析方法，计算得到了返回器气动辨识结果的偏差区间。

3.1 测量误差因素

返回器飞行试验测量参数主要包括：惯性系统输出的角速率、加速度，以及导出量姿态角等数据；GPS系统输出的高度、经度、纬度，以及导出量速度等数据；以及大气密度、风场等大气数据。根据大气研究部门提供的数据，大气密度的相对偏差如图4所示，可见高度越高，大气密度偏差越大。

图4 大气密度的相对偏差随高度变化Fig.4 Relative deviation of atmospheric density vs. altitude

影响捷联惯导系统的误差因素主要有比例因子误差、交叉耦合误差、零位误差等，其中零位误差是最主要的误差因素。姿态角的误差主要来源于积分初值误差，以及角速率误差引起的积分积累误差。因此，本文在进行误差分析时，只考虑主要的误差因素，如加速度、姿态角的常值误差，表1给出了具体的量值[17]。GPS系统输出的高度、速度是进行参数估计的重要参数，根据GPS系统的指标参数，高度精度为15 m，速度精度为1 m/s。结合风速的测量误差，速度分量的测量误差取为2 m/s。

表1 主要测量参数的误差Table 1 Measurement errors of main parameters

3.2 各误差因素的影响

根据表1的主要参数测量精度，将各参数的测量误差分别加入到经过预处理和重建的飞行试验数据中，计算大气密度、高度、加速度、姿态角、速度等测量参数产生的配平迎角、升阻比、轴向力系数、法向力系数等参数的偏差。

大气密度和飞行高度主要影响气动力系数的估计结果，对配平迎角和升阻比没有影响。图5为大气密度误差产生的气动力系数和升阻比相对偏差。30 km以下，偏差小于3%。随着高度增加，误差也相应增加，90 km以上，偏差大于10%。可见大气密度误差对气动系数估计偏差的影响较大，因此大气密度是气动参数估计的第一误差源。如图6，飞行高度的影响不明显，最大偏差约为0.2%。

图7为加速度误差产生的气动力系数和升阻比相对偏差。可见在动压较高的时间段，加速度误差影响不明显。加速度量值较小的90 km以上的高空，加速度误差的影响很大，产生的轴向和法向力系数最大相对偏差分别为2.2%和6.3%，升阻比相对偏差最大可达23%。加速度主要影响气动力系数和升阻比的估计结果，对配平迎角没有影响。

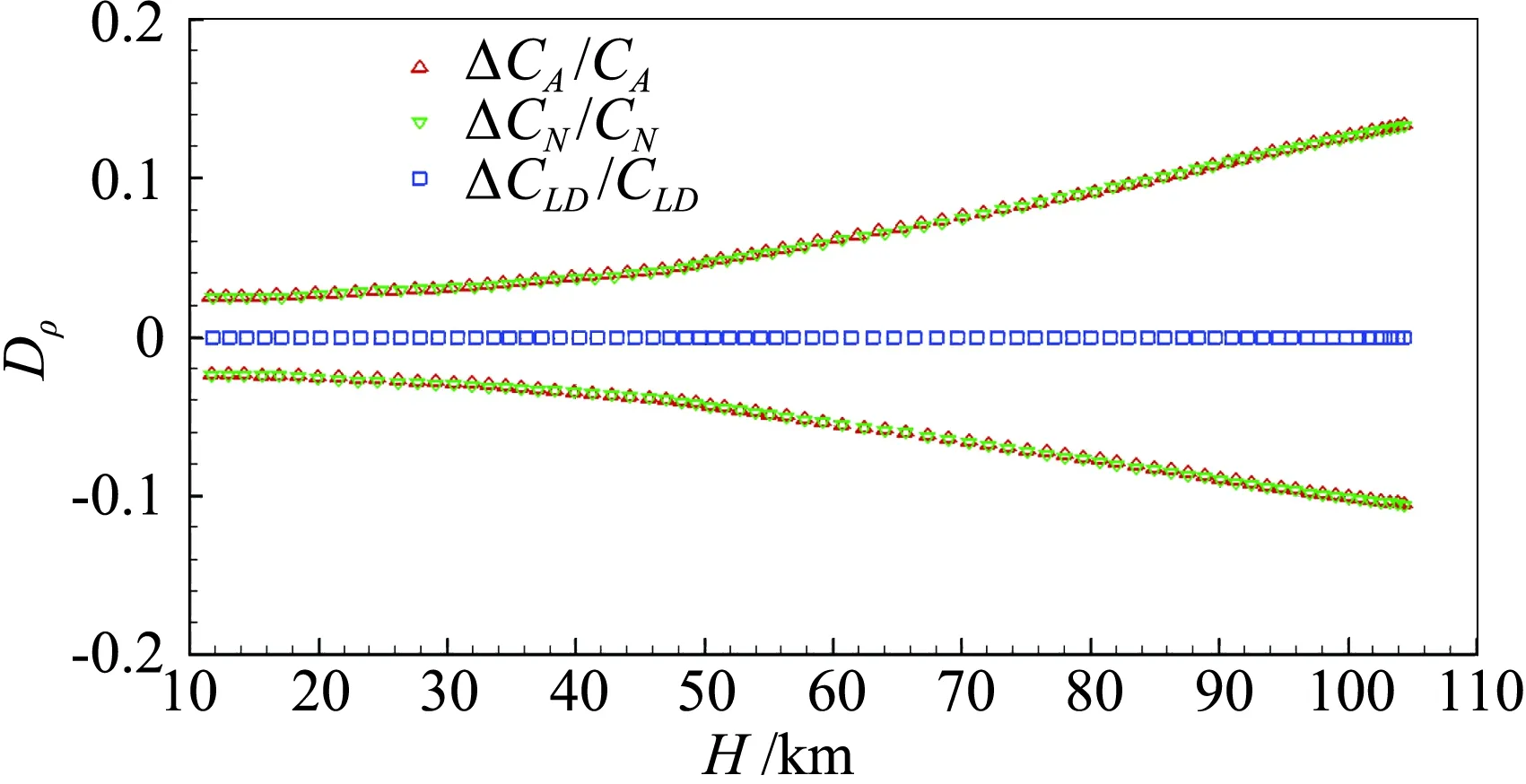
图5 密度误差产生的气动力系数和升阻比偏差Fig.5 Relative deviation of aerodynamic coefficients and lift-drag ratio by atmospheric density

图6 高度误差产生的气动力系数和升阻比偏差Fig.6 Relative deviation of aerodynamic coefficients and lift-drag ratio by altitude

图7 加速度误差产生的气动力系数和升阻比偏差Fig.7 Relative deviation of aerodynamic coefficients and lift-drag ratio by acceleration

图8和图9分别给出了速度误差产生的配平迎角和气动力参数偏差。可见开伞前，由于速度较小，且方向接近于垂直地面，速度产生的迎角偏差可达1°左右，升阻比偏差最大约为7%。可见，速度主要影响再入末段迎角和升阻比估计结果，对气动力系数的影响较小。

图10和图11分别给出了姿态角误差产生的配平迎角和气动力参数偏差。可见，姿态角误差产生的迎角偏差最大约为0.12°，升阻比偏差最大为2%左右。姿态角对气动力系数没有影响。

图8 速度误差产生的配平迎角偏差Fig.8 Deviation of trim angle by velocity

图9 速度误差产生的气动力系数和升阻比偏差Fig.9 Relative deviation of aerodynamic coefficients and lift-drag ratio by velocity

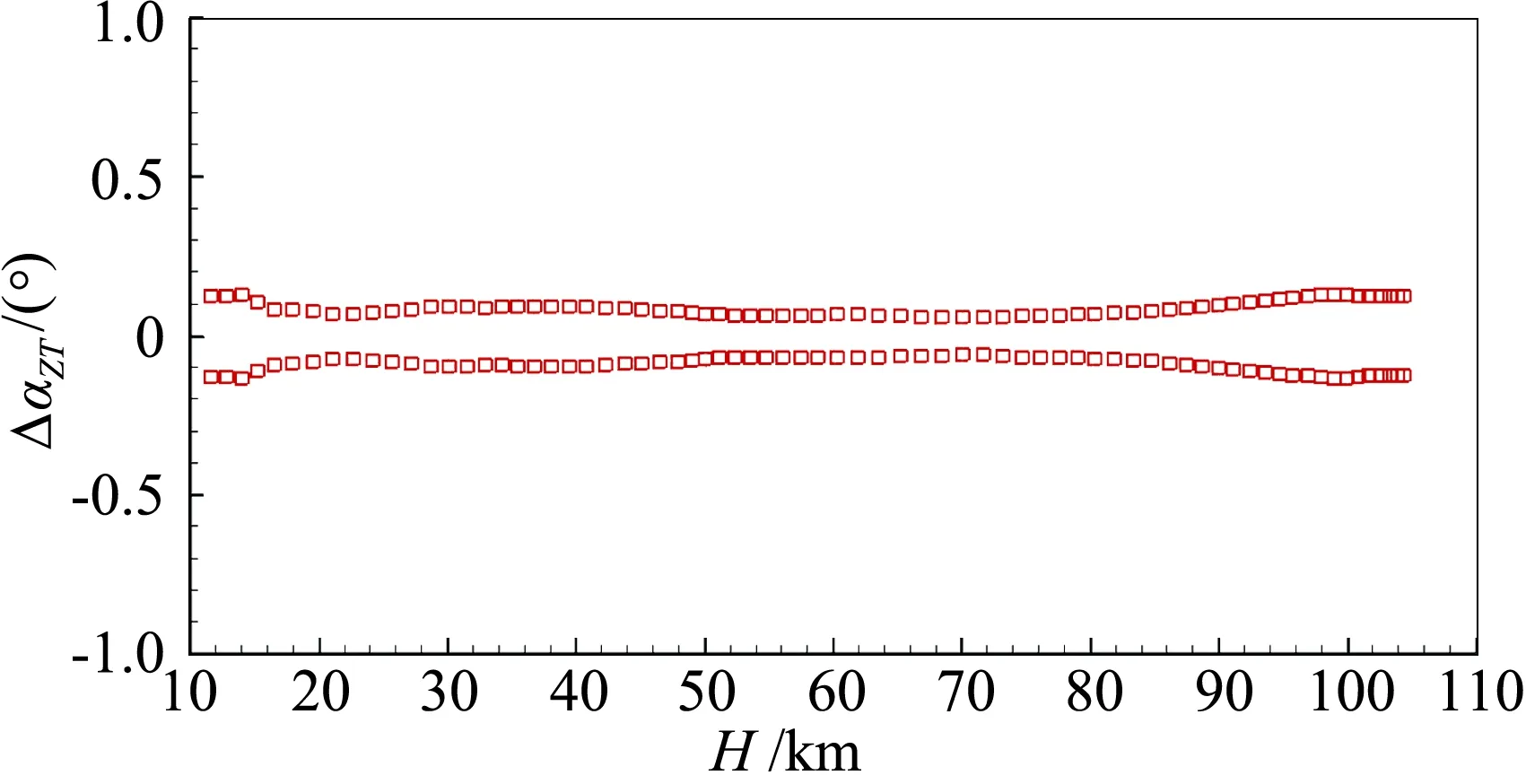
图10 姿态角速度误差产生的配平迎角偏差Fig.10 Deviation of trim angle by attitude angle

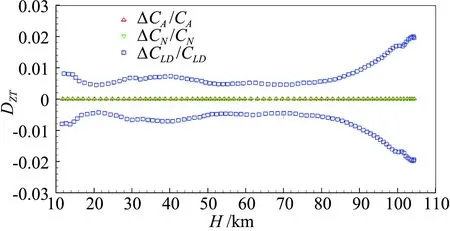
图11 速度误差产生的气动力系数和升阻比偏差Fig.11 Relative deviation of aerodynamic coefficients and lift-drag ratio by attitude angle

3.3 误差因素的综合影响

为了分析各测量参数误差的综合影响，各测量参数在表1所示的误差区间范围内按均匀分布随机取值，组成一组误差矢量Δri。以同样的方法，共生成N组随机误差矢量。

把每组误差加入到处理后的测量数据中，其中迎角、升阻比和气动力系数采用式(1)～式(9)估计。共得到N组估计结果，并与不加测量误差的估计结果相减，生成气动估计偏差。

Δri= (Δρi,Δhi,Δωxi,Δωyi,Δωzi,Δaxi,Δayi,

Δazi,ΔVxi,ΔVyi,ΔVzi,Δφi,Δψi,Δγi)(12)

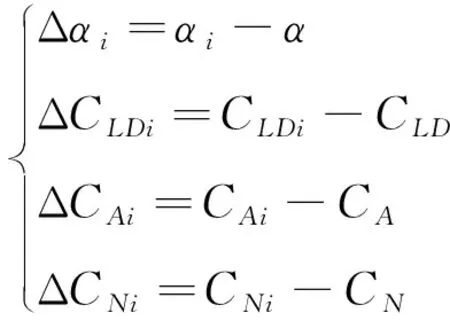
然后，从N组偏差数据中，求出每一时间点对应的最大偏差值，作为该时间点的偏差边界。以迎角为例，其偏差边界为

σα=±max(Δαi)(14)

气动力矩导数、喷流控制力矩等参数利用式(10)～式(11)进行参数估计。其偏差区间采用文献[14]的修正克拉马-罗界作为偏差边界。

图12给出了所有误差因素影响下的配平迎角，配平迎角的偏差区间。在开伞前，配平迎角的估计偏差稍大，最大值约为1.2°，主要影响因素为速度和姿态角误差。图13给出了所有误差因素影响下的气动力系数和升阻比偏差区间。在100 km以上的高空，轴向力系数的最大相对偏差约为16.3%，法向力系数的最大相对偏差约为20.8%，升阻比的最大相对偏差约为26.1%。到90 km的高度，气动力系数的最大相对偏差降到10%左右，升阻比的最大相对偏差则降到了3%以内。

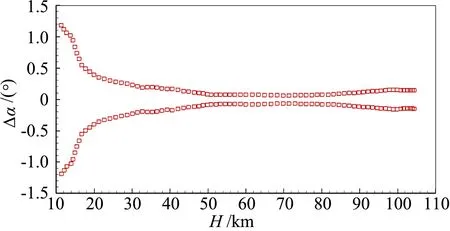
图12 所有误差产生的配平迎角偏差Fig.12 Deviation of trim angle by all errors

图13 所有误差产生的气动力系数和升阻比偏差Fig.13 Relative deviation of aerodynamic coefficients and lift-drag ratio by all errors

图14中红色方形符号为俯仰力矩导数的辨识结果，蓝色“工”形符号为修正克拉马-罗界。俯仰力矩导数小于零，说明返回器再入全程是静稳定的。在40～80 km的主要再入飞行段，俯仰力矩导数的相对偏差为5%左右。

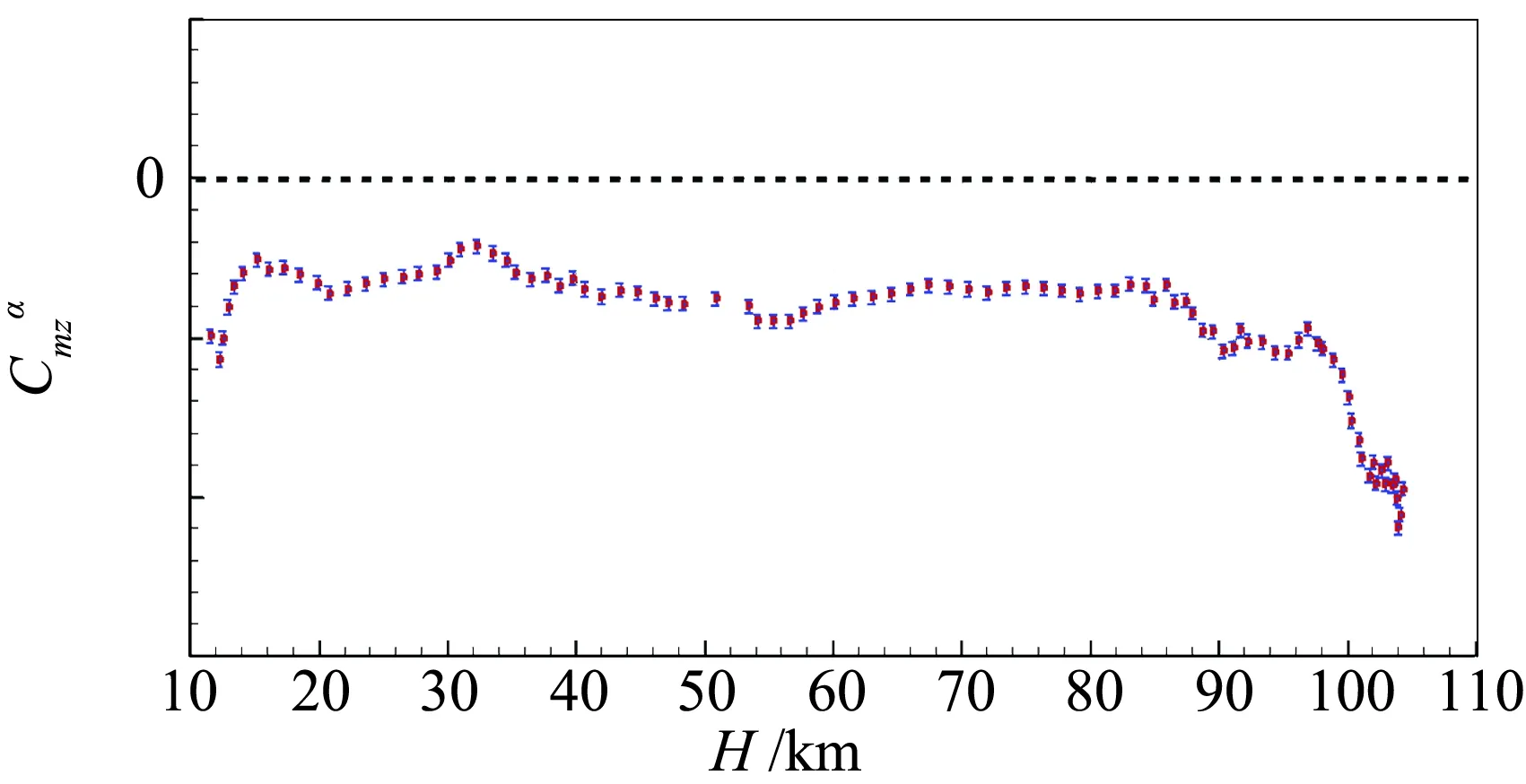
图14 俯仰力矩导数及其偏差Fig.14 Pitch moment derivatives and deviations

图15中红色方形符号为正向滚转控制发动机推力的辨识结果，绿色三角符号为负向滚转控制发动机推力的辨识结果，蓝色点划线为所有辨识结果的平均值，黑色虚线为地面设计结果。辨识结果平均值略大于地面设计结果3.1%，标准差与平均值之比为5.04%。图16为各辨识结果的修正克拉马-罗界与辨识结果之比，其值也在5%附近，说明修正克拉马-罗界与标准差比较接近。

综上可以看出如下规律：在返回器的绝大部分再入飞行时间里，配平迎角的估计精度都比较高，飞行试验结果是可靠的。由于升阻比不受大气密度、高度误差的影响，在动压较大的时间段，升阻比精度较高，只有气动加速度很小的时间段，受加速度测量误差的影响，升阻比偏差较大。气动力系数受大气密度、加速度、高度、速度等因素的综合影响，相对偏差稍大，但动压较大的主要飞行段，其相对偏差小于5%，只有气动加速度很小的时间段，受加速度测量误差的影响，相对偏差达到了10%以上。因此，为了获取更高精度的高空稀薄大气条件下的气动力参数，安装专用的小量程加速度计，提高加速度测量精度是非常必要的。同时，提高大气密度的测量精度，也是提高气动系数辨识精度的有效途径。利用修正克拉马-罗界作为气动力矩导数和喷流推力辨识结果的偏差估计结果是可行的，喷流推力的修正克拉马-罗界与标准差统计结果比较接近。

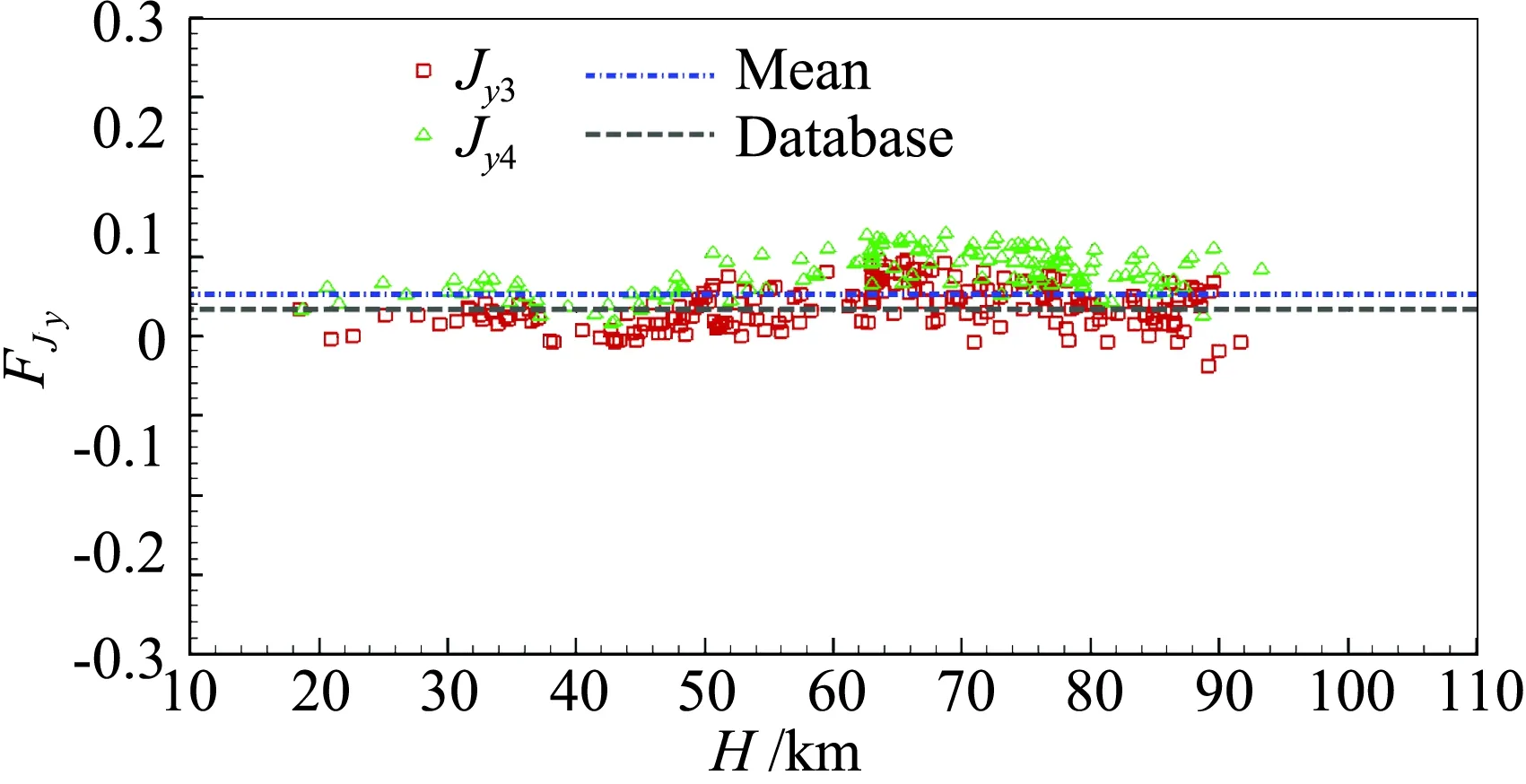
图15 滚转控制发动机推力辨识结果Fig.15 Force of roll control engine from flight data

图16 滚转控制发动机推力相对偏差Fig.16 Relative deviation of roll control force

4 结 论

本文针对返回器飞行试验，研究了返回舱气动参数辨识与偏差分析方法，并利用月地高速再入返回器飞行试验测量数据，对配平迎角、升阻比、气动力系数、气动力矩导数、喷流控制发动机推力等参数进行了辨识计算，分析了各误差因素产生的气动偏差，以及综合起来产生的气动偏差。主要结论为：

(1) 飞行试验的大气密度、加速度、姿态角、高度、速度等参数的测量误差是产生气动参数辨识偏差的因素，其中大气密度、加速度误差是产生气动力系数辨识偏差的主要因素，姿态角、速度误差是产生配平迎角偏差的主要因素，加速度、速度、姿态角误差是产生升阻比偏差的主要因素。

(2) 配平迎角的估计精度很高，飞行试验结果是可靠的。在动压较大的时间段，升阻比偏差较小，只有动压很小的高空稀薄大气段，升阻比偏差较大。气动力系数受大气密度、加速度等因素的综合影响，相对偏差稍大。特别是高空稀薄大气段，为了获取更高精度的高空气动力参数，安装专用的小量程加速度计，提高加速度测量精度是非常必要的。

(3) 本文利用修正克拉马-罗界作为准则，获得了气动力矩导数和喷流推力辨识数据的偏差估计结果，实践证明该偏差估计方法是可行的。本文获取的月地高速再入返回器气动参数的偏差结果，可以为返回器设计分析提供依据。