展向动量测定法与前掠翼流动机理研究

薛榕融, 叶正寅, 王 刚, 武 洁

(西北工业大学 航空学院, 陕西 西安 710072)

0 引 言

早期基于势流理论，得到前掠翼大量理论成果，但其研究工作中相同翼展和梢根比下前掠翼前缘掠角总小于后掠翼前缘掠角，同时前掠翼后缘掠角大于后掠翼，在这种情况下，得到低马赫数下前掠翼的优点[9-11]：(1) 更小的诱导阻力；(2) 更大的升力线斜率；(3) 逐渐减弱的抬头趋势；(4) 更小的结构展长：(5) 与当量后掠翼相比更小的质量；(6) 前掠翼根首先引起流动分离，能同时保证副翼效率和滚转阻尼，在流动分离的情况下拥有更好的侧滑稳定性和操纵效率；(7) 跨声速时无明显优势，超声速下前掠翼甚至存在气动上的劣势(见图1)。

图1 不同马赫数下前掠翼与后掠翼Fig.1 Forward- and aft-swept wings at different Mach Numbers

但是，NASA在X-29的设计实验试飞结果[11-17]却与上述结论中(1)(2)相悖。对采用圆弧翼型的翼身组合体进行风洞实验[10,15]中，通过正吹和反吹获得前掠32°与后掠60°机翼的低速纵向气动性能并进行对比。来流条件马赫数为0.3、雷诺数为1.4×106时得到前掠翼的升力线斜率小于后掠翼，前掠翼最大升力系数(CLmax=0.96，αCLmax=40°)小于后掠翼 (CLmax=1.2，αCLmax=28°)，但失速迎角大于后掠翼。但是两机翼掠角不同，并不是在同一基础上进行对比，不能全面反应两者性能的优劣[3]。

Poll[18]等针对无根梢比尖前缘双凸翼型机翼，采用不同掠角方向和边条进行了马赫数为0.1的低速风洞试验，实验结果显示前掠翼升力线性段为-5°～9°，后掠翼升力线性段为-5°～13°，两者在小迎角时升力线斜率基本相同，前掠翼在迎角35°取得最大升力系数为1.15，后掠翼在迎角40°取得最大升力系数为1.12，结论与NASA结论相差很大。

西北工业大学张彬乾与德国布伦瑞克工业大学Laschka对前掠翼及前掠翼鸭翼布局[19-21]进行了一系列的低速风洞实验，对前掠翼良好的升阻特性、力矩特性与失速特性进行了验证，并对前掠翼前后缘涡系对升阻力特性的影响进行分析，进而对利用边条和鸭翼对前掠翼构型的流动控制进行研究。

美国安柏瑞德航空大学Traub[22]等研究了箭形机翼的边条位置对机翼纵向气动性能的影响，对无梢根比的Λ=-65°、Λ=65°的前后掠翼，展弦比均为2，分别在前后缘根部加装翼展长度30%的边条翼，在风速25 m/s，Re=1.8×105下进行风洞实验。实验显示在迎角大于4°时前掠翼升力小于后掠翼。流线显示前掠翼翼根有较大范围的分离区，后掠翼翼尖的分离则相对较小。

刘文法[23]针对40°的前掠翼和后掠翼模型在Ma=0.4时进行CFD计算结果，发现在α<16°时后掠翼升力系数大于前掠翼，α>16°前掠翼升力较大，同时前掠翼失速迎角为32°，后掠翼仅为12°，前掠翼的失速性能明显好于后掠翼。

如图1所示，通过对电压采样值进行平方、开方以及数字滤波等一系列运算得到。电压通道输入10～1 000 MV的信号时电流有效值的误差小于0.5%。

面对文献中的不同结论，深入分析前掠翼气动特性，从物理机制上探讨前掠翼的流动机理，增加对前掠翼流动和气动特性的理解是非常迫切的工作。为避免机翼其他参数对流动的影响，本文设计采用了相同翼型剖面、相同展弦比、无根梢比的前掠45°(Λ=-45°)与后掠45°(Λ=45°)机翼，提出了展向动量测定法，结合数值模拟方法在Ma=0.2、Re=4.6×106条件下深入分析前掠翼与后掠翼的纵向气动性能，结合展向动量测定法定量分析了前掠翼与后掠翼的流动机理。

1 算例验证

为验证数值模拟的准确性，本文采用慕尼黑工业大学Breitsamter等[1]在2001年慕尼黑工业大学流体力学实验室开展的针对前掠翼身组合体的低速风洞实验进行验证。风洞实验区直径1.5 m，长3 m，最大风速为55 m/s，湍流度为0.3%～0.4%。模型为机翼前掠40°的翼身组合体，机翼翼型为NACA64A010，如图2所示。试验风速为40 m/s，基于参考弦长的Re=0.46×106。本文分别采用课题组自研的基于雷诺平均N-S方程流场求解器General Fluid & Structure Interaction (GFSI) 与ANSYS FLUENT进行数值模拟，采用结构化网格，机体面网格数为37 820，体网格数为5 076 260，首层网格y+约等于1，采用SST湍流模型，计算与风洞实验结果对比见图3。

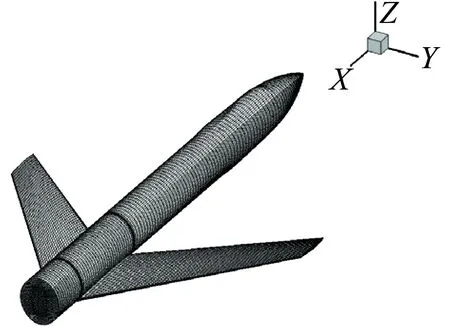
图2 前掠翼几何模型与面网格Fig.2 Geometry model and surface mesh of forward-swept wing body

由图3可以看出，GFSI，FLUENT计算结果与实验结果基本吻合，而FLUENT结果在大迎角时计算值偏大，GFSI对前掠翼的数值模拟计算误差更小，故选用GFSI作为数值模拟求解器。

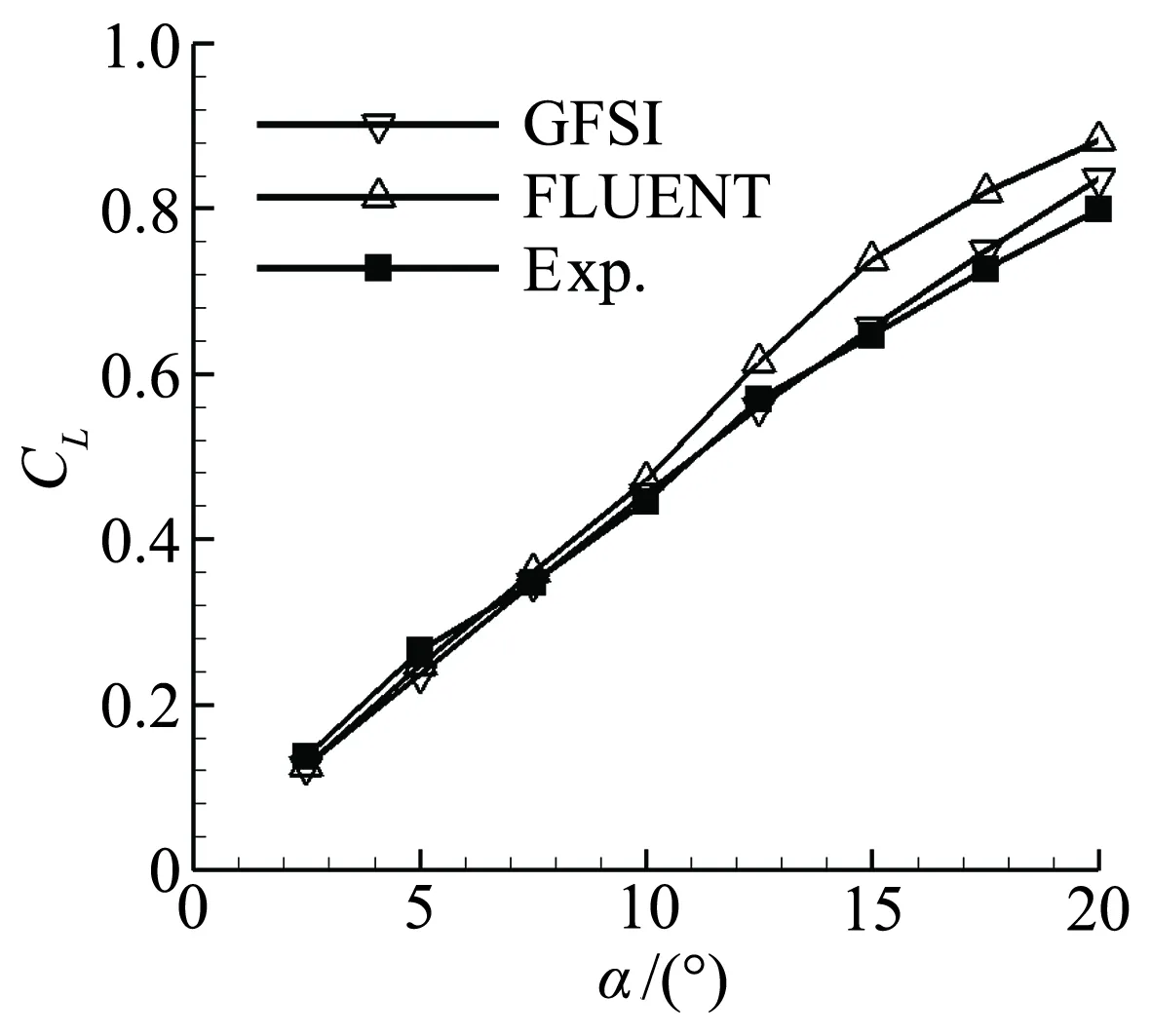
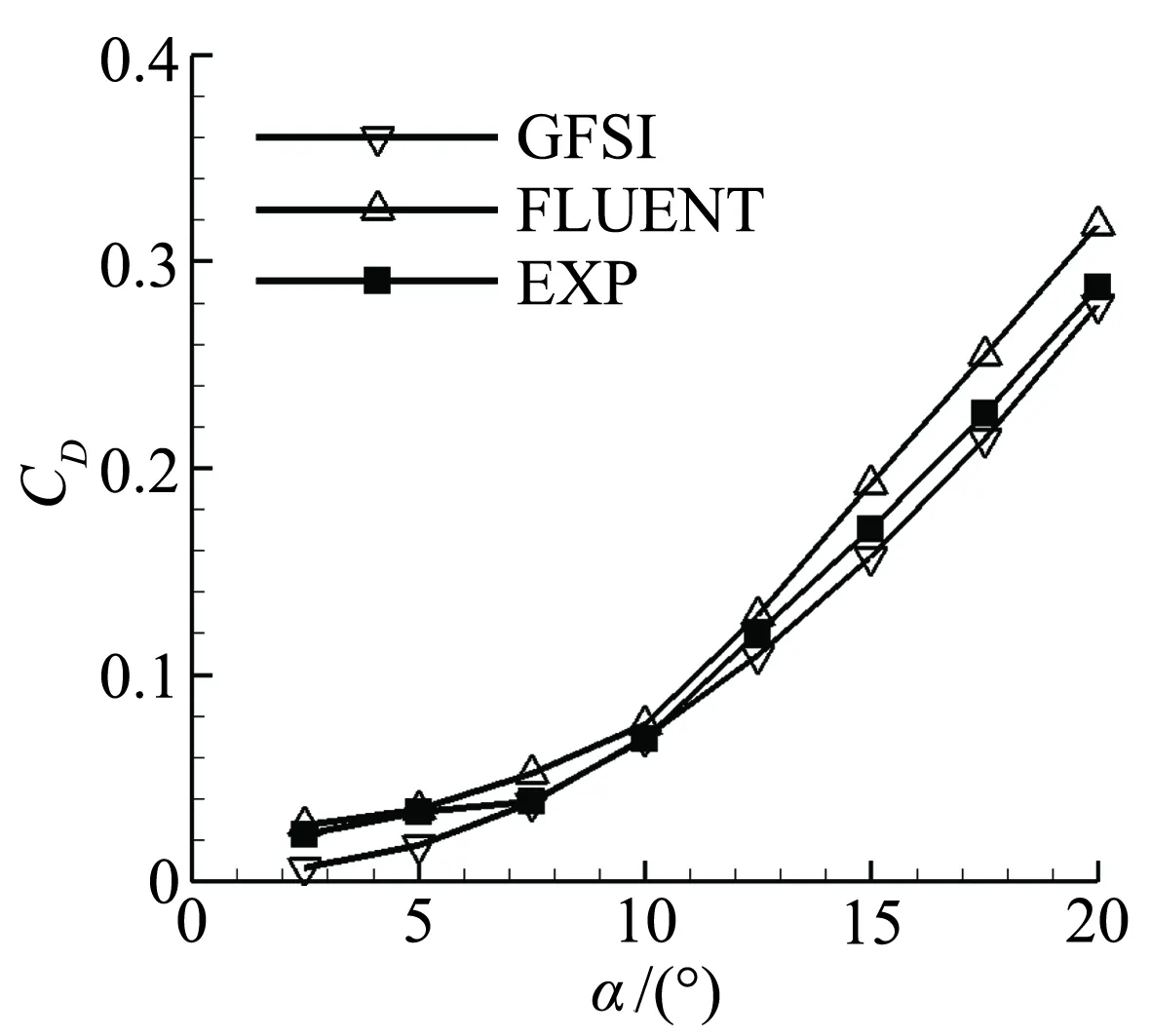
图3 翼身融合体升阻力随迎角变化Fig.3 Wing body’s lift and drag

2 展向动量测定法

根据牛顿第二定律(式1)，施加在物体表面的力等于物体动量的时间变化率。对于飞行器来说，飞行器无动力飞行过程中受到的力即源自包含飞行器控制体内的动量的时间变化率。包含飞行器控制体内动量的时间变化率分为两部分：1)经由控制体表面单位时间净流入(流出)的动量(动量通量)；2)由非定常扰动引起单位时间控制体的动量增量。在定常流场计算中式(2)中∂/∂t≡0，则作用在物体上的力仅由动量通量项决定，则得到式(3)。

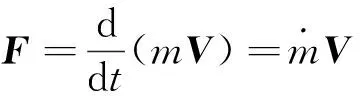
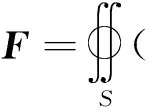
对前掠翼翼升力机理进行分析，将机翼沿展向分为10个控制体(图4)，并对每个控制体内的动量通量进行积分计算，深入分析前后掠翼升力物理机制上的异同。

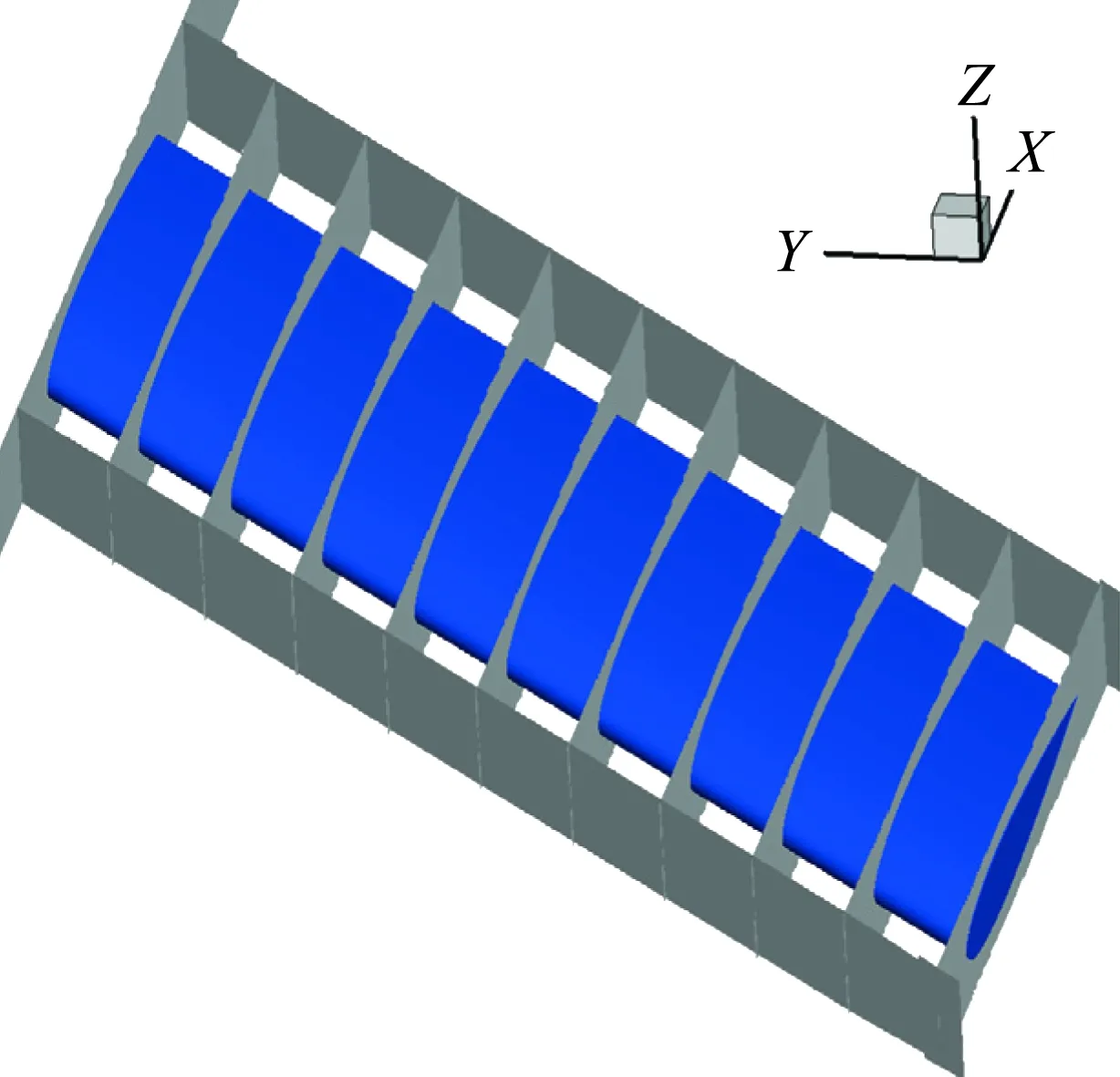
图4 机翼沿展向控制体示意图Fig.4 Spanwise control body for momentum method

3 前掠翼模型设计与网格

对前掠翼气动性能的研究中，大多文献的研究中未能避免根梢比对性能的影响。在NASA的实验中甚至采用机翼模型正反吹来进行性能的对比分析，造成模型前掠翼为32°掠角，后掠翼为60°掠角，掠角的差异对性能的影响也未能避免。为避免其他机翼参数对机翼性能产生影响，本文设计了前掠45°(Λ=-45°)与后掠45°(Λ=45°)机翼进行计算与对比分析，前后掠机翼均采用NACA0012翼型，展长为4 m，展弦比均为4，根梢比均为1。

数值计算采用半翼展模型，空间流场为机翼参考弦长的100倍(前后上下左各100倍)。为排除网格对数值模拟结果的影响，采用结构化网格进行空间离散，前后掠翼面网格分布完全相同，附面层相同，体网格数目也完全相同。分别采用两套网格(带附面层和不带附面层)进行有黏和无黏流场计算，其中黏性网格机翼面网格数为12 176，首层网格y+约等于1，附面层为30层，体网格数为6 802 039；无黏网格机翼面网格数量为13 275，体网格数为3 841 201。机翼外形与网格见图5、图6、图7。

采用GFSI作为流场求解器，计算状态为Ma=0.2，Re=4.6×106。采用绝热壁面边界，迎风格式为Roe格式，其中有黏计算采用SST湍流模型。

图5 前掠翼与后掠翼面网格Fig.5 Forward- and aft-swept wings’ surface grid

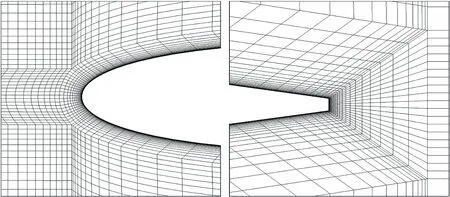
图6 有黏网格附面层网格局部放大图Fig.6 Boundary layer mesh of viscous computation

图7 计算流域及远场网格Fig.7 Flow field and far field grid

4 前掠翼升阻力特性分析

数值模拟计算得到前后掠翼升阻力特性曲线，如图8、图9、图10。

图8 前后掠翼升力特性曲线Fig.8 Forward- and aft-swept wings’ lift curves

由图8中小迎角下前掠翼与后掠翼升力均随迎角增加而线性增长，无黏和有黏条件下相同迎角时前掠翼的升力系数均小于后掠翼，且升力线斜率小于后掠翼，升力表现稍劣。无黏计算无法准确计算大迎角分离流动，其升力变化不符合物理规律，无法体现流动的非线性。有黏计算中前掠翼最大升力系数CLmax=1.08小于后掠翼CLmax=1.32，失速迎角αstalling=26°大于后掠翼αstalling=24°，失速后后掠翼升力迅速减小，而前掠翼升力减小则十分缓慢，前掠翼大迎角失速特性较好。

对于图9，小迎角下前掠翼阻力在各迎角均小于后掠翼，且两者之间阻力差随迎角增加不断扩大。但7°～8°迎角前掠翼阻力突增，主要是由于前掠翼翼根附面层堆积，使得翼根更早发生分离，前掠翼阻力大于后掠翼。而在后掠翼失速后，后掠翼阻力逐渐与前掠翼持平。取无限翼展机翼计算其阻力CD_in，则三维有限翼展机翼翼尖下洗引起的诱导阻力为CD_induced=CD-CD_in，计算结果如图11。有黏计算中前掠翼小迎角下诱导阻力均小于后掠翼，从而验证了前掠翼诱导阻力小的结论。

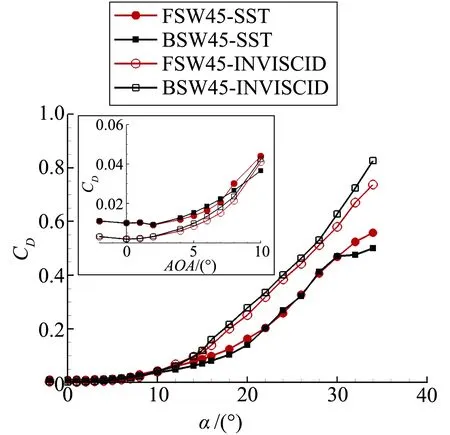
图9 前后掠翼阻力特性曲线Fig.9 Forward- and aft-swept wings’ drag curves

图10给出前掠翼与后掠翼升阻比曲线。无黏条件下后掠翼升阻比在3°迎角之前好于前掠翼，3°迎角之后前掠翼升阻比大于后掠翼，由于前掠翼升力在整个迎角范围内均小于后掠翼，其升阻比在3°迎角之后优于后掠翼的主要原因在于前掠翼相比后掠翼更小的诱导阻力。而有黏条件下前掠翼小迎角气动效率也小于后掠翼，仅在最大升阻比位置处(α=6°,(CL/CD)max=18.2)优于后掠翼(α=6°,(CL/CD)max=17.9)，之后由于前掠翼翼根分离阻力上升，其气动效率迅速下降，直到失速迎角附近前掠翼与后掠翼气动效率相当。另外说明黏性作用对前掠翼升阻力特性影响比较大，具体地说黏性作用使得前掠翼在无黏小迎角条件下的升阻比优势丧失。主要的原因有两点：(1) 前掠翼有黏条件下升力较无黏条件下平均下降8.94%(1°≤α≤6°)，后掠翼相同条件下平均下降7%；(2) 前掠翼有黏条件下阻力较无黏条件增加3.5%，后掠翼相同条件下平均增加3.14%。黏性作用导致前掠翼在有黏条件下气动效率劣于后掠翼。这说明文献中采用势流理论对前掠翼气动性能进行预测是不合理的，得到的结论与真实情况往往不同。

图10 前后掠翼升阻比特性曲线Fig.10 Forward- and aft-swept wings’ lift/drag ratio

图11 前后掠翼小迎角诱导阻力Fig.11 Forward- and aft-swept wings’ induced drag

5 前掠翼流动机理分析

提取有黏计算结果小迎角(0°～6°)时机翼升力沿翼展方向分布如图12。图中相同迎角下前掠翼升力向翼根汇聚，升力翼根处大于后掠翼，翼梢处小于后掠翼。前掠翼升力展向分布更接近椭圆分布。根据普朗特升力线理论，有限翼展机翼升力分布为椭圆分布时其诱导阻力最小，则升力展向分布特征决定了前掠诱导阻力小，这也从图11中得到验证。

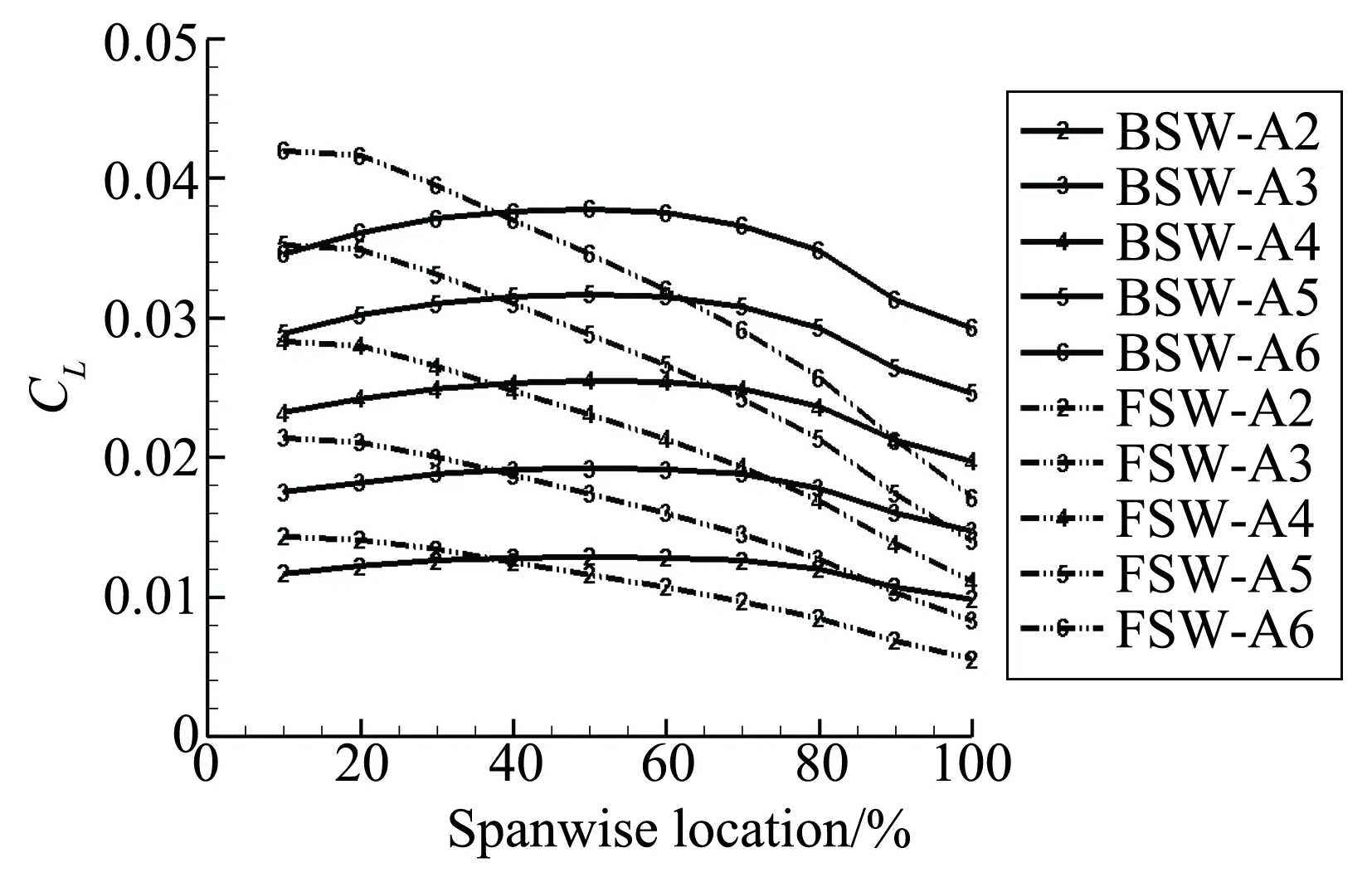
图12 前后掠机翼升力沿展向分布Fig.12 Forward- and aft-swept wings’ spanwise lift distribution

利用展向动量测定法对前掠翼与后掠翼的升力形成机理进行分析。从机翼绕流流场的选取固定六面体控制体区域，将控制体沿展向分为10个局部控制体(见图4)，由于X方向的动量通量项对升力贡献有限，为方便计算，仅取Z方向的动量通量项(式4)对升力的形成机制进行分析。由式4计算机翼不同展向位置控制体内(式中密度ρ，分速度u、v、w均为无量纲量)，得到不同展向位置Z向动量通量分布如图13所示。

图13 Z向动量通量沿展向分布Fig.13 Z direction spanwise momentum flux distribution

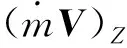
6 前掠翼翼根弯矩的特点

前掠翼靠近翼根处翼面升力大，靠近翼梢处翼面升力小的升力分布形式对结构也带来显而易见的优势，即翼根弯矩比后掠翼更小，计算两机翼翼根弯矩Cmx随升力变化如图14，前掠翼与后掠翼翼根弯矩与升力基本成线性变化关系，相同升力下前掠翼的翼根弯矩仅为后掠翼的89.4%，这将对前掠翼布局的结构设计带来极大的裕度，对提高布局整体刚度和结构减重带来极大的优势。

图14 前后掠翼翼根弯矩随升力变化Fig.14 Forward- and aft-swept wings’ bending torque

7 结 论

利用课题组研发的流场求解器GFSI进行前掠翼标模计算，计算结果与实验结果吻合良好。设计了相同翼展、相同弦长、根稍比均为1的前掠45°机翼和后掠45°机翼，对其低速气动性能进行了有黏和无黏计算，对其升阻力特性进行对比分析，分析计算了其诱导阻力。提出展向动量测定法对前掠翼升力形成机理进行深入分析，进一步探讨了前掠翼升力分布特征对机翼翼根弯矩特性的影响。综上得到结论如下：

(1)前掠翼升力的展向输运形成了典型的翼根升力大，翼尖升力小的接近椭圆分布特点，其诱导阻力更小。而后掠翼升力展向输运相对较为微弱。

(2)有黏条件前掠翼下升力较大，阻力增加也更多，黏性作用对前掠翼气动效率影响更大，说明以往文献中仅采用势流理论对前掠翼升力特性预测是不合理的，同时 “前掠翼升力大，升力线斜率大”的结论也是不准确的。对前掠翼的流体计算应着眼于有黏条件的计算。

(3)小迎角时前掠翼气动效率低于后掠翼，仅在最大升阻比的迎角下前掠翼气动效率优于后掠翼，在中等迎角前掠翼气动效率较低，但前掠翼失速迎角大，失速后升力缓慢减小，大迎角失速特性优异。

(4) 在相同升力下前掠翼翼根升力大，翼尖升力小的升力分布特性使得前掠翼翼根弯矩小于后掠翼翼根弯矩，对机翼结构设计减重提供了优势。