大气边界层模式中随机参数的反演与不确定性分析∗

颜冰 黄思训2)† 冯径

1)(国防科技大学气象海洋学院,南京 211101)

2)(上海财经大学,计算科学与金融数据研究中心,上海 200433)

(2018年5月24日收到；2018年7月10日收到修改稿)

1 引 言

行星大气边界层的研究对于气候模式和数值预报模式的发展很重要,边界层模式的选择非常关键[1].完整的边界层模式过于复杂不利于计算与分析,简化的Ekman模式过于简单无法描述边界层的非线性特征.Tan和Wang[2]提出的广义Ekman动量近似模式既保留了惯性项的作用,又考虑了湍流黏性系数随高度的变化,是一个研究大气边界层实用且有效的模式.在该模式中,一个非常重要的参数就是湍流黏性系数,它是反映湍流效应的参数[3].通常,直接测量出准确的湍流黏性系数较为困难,所以人们希望得到不确定性较小的湍流黏性系数.

根据湍流黏性系数的分布计算出风速的分布,叫做“正向不确定量化”或者 “预报模式”[4].实际上湍流黏性系数是确定的,但是由于观测误差等原因无法准确获知其准确值,仅能得到大致的分布,所以必须收集更多的信息来缩小分布的范围.通过风速的观测反演降低湍流黏性系数的不确定性,叫做“逆向不确定量化”或者 “逆模式”[5].不确定性问题的研究比确定性问题困难,同时,因为反问题是不适定问题,这意味着解可能不存在、解存在但是多解或解不稳定.反问题的研究比正问题的研究困难很多[6],所以逆向不确定问题的研究更加困难,而且由于观测数据存在着不可避免的误差,观测中包含的信息通常不足以确定所有的不确定参数,所以参数的不确定性不能被消除,只能降低.

反问题一般根据贝叶斯理论来求解,利用给定的参数先验分布结合模式输出量计算得到参数的后验分布.但是它在大部分情况下都不能被解析地表达,所以必须通过采样的方法来表达后验分布的不确定性,常用的方法有马尔可夫链蒙特卡罗抽样方法(Markov chain Monte Carlo,MCMC),基于Metropolis-Hastings算法[7],Gibbs采样器[8],粒子滤波[9].但是这些采样的方法需要大量的样本,每一个样本均需要进行一次模式的计算,所以占用了大量的计算资源.

一种常用的能够解析计算后验分布的方法叫做Kalman滤波[10],它的要求是模式必须是线性的,而且先验分布与观测误差分布必须是正态分布.这种情况下模式参数的后验分布同样是正态分布,它的特征能够用前两阶矩即均值与方差来表征.但是实际大部分大气海洋数值模型是非线性的,而且观测模型也是非线性的.对于非线性系统,可以用Kalman滤波得到一个较为准确的近似解,其难点在于在耗费较少计算资源的情况下怎样由参数的分布计算得到模式输出的分布.扩展Kalman滤波方法(extended Kalman filter,EKF)是Kalman滤波的近似,将非线性模式在分析值处进行Taylor展开到一阶,略去高阶项,再进行Kalman滤波过程[11].但是在计算过程中由于非线性会导致协方差矩阵的不稳定性,而且计算量大.集合Kalman滤波方法(ensemble Kalman filter,EnKF)首先利用蒙特卡罗法来求解不确定性在非线性系统中的传播[12,13],然后计算得到Kalman增益矩阵.Evensen[13]最早把EnKF用到数据同化中,他利用概率论上一些理论与简单数值实验说明该方法的可行性.由于EnKF便于实施,故在很多领域都得到了广泛的应用.但是由于EnKF基于蒙特卡罗方法,所以其准确性就与样本的大小密切相关,而大模式样本需要非常多的计算资源.Kalman滤波类的方法通常是采用递归的方式来进行,对于每个数据序列上的数据均进行一次滤波计算,这样前一次的后验分布作为后一次的先验分布,这种过程被称为“顺序数据同化”.

混沌多项式展开(polynomial chaos expansion,PCE)可以作为蒙特卡罗法的代替,其本质就是利用一组正交随机多项式展开来表达不确定性[14,15].根据Askey方案[16],当分布已知的情况下,最优的正交基函数就是确定的,所需要求解的就是待定的多项式系数.当系数求解出来后,就会很快求出随机变量的统计矩[17].所以混沌多项式展开方法的关键就是求解多项式系数.有很多方法可以求解此系数,例如随机Galerkin方法[15],回归法[18],概率配点法[19].本文中利用回归法来求解系数,它是一种非浸入式方法,不需要对原模式计算代码进行更改,只需要进行少量的采样,然后求解方程组即可求得系数.该方法易于理解,便于实施,而且在消耗较少资源的情况下能达到较高的精度.模式输入与输出变量采用混沌多项式表达,利用基函数的正交性求出输出变量的统计矩,避免了使用蒙特卡罗法,能够节省计算资源.这种方法就被称为基于混沌多项式的集合Kalman滤波方法(polynomial chaos-ensemble Kalman filter,PC-EnKF)[20].

本文试图利用PC-EnKF求解观测值为风速的情况下湍流黏性系数的后验分布,以降低系数不确定性和提供更可靠的范围.而且,还可以根据先验的风速分布确定出有效观测的区域,为观测点位置的选择提供强有力的指导.由于实际观测数据难以获得,所以本文采用数值实验的方式验证该方法的有效性和可靠性.本文第2部分介绍随机广义Ekman动量近似模式以及预报模式的求解方法；第3部分介绍逆模式以及Kalman滤波类算法；第4部分介绍数值实验及其分析；第5部分给出总结与讨论.

2 随机广义Ekman动量近似模式

2.1 模 式

本文采用Tan和Wang[2]提出的广义Ekman动量近似模式(general Ekman momentum approximation model,GEM),该模式简单且同时保留了系统的非线性特征.将模式中湍流黏性系数由确定性的参数变为符合某种分布的不确定性参数,此时该模式演变成广义Ekman动量近似的随机边界层模式(stochastic general Ekman momentum approximation model,SGEM).模型如下:

其中湍流黏性系数K是随高度z变化的随机变量,ξ代表的是随机变量,(u,v)代表(x,y)方向上的风速分量；

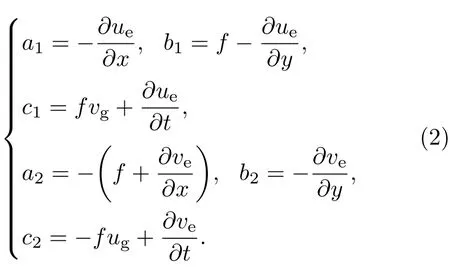
(2)式中,f代表Coriolis参数,在本文中假定为常数；(ue,ve)为经典Ekman模式的解,(ug,vg)为地转风.方程(1)的边界条件为:u|z=0=0,v|z=0=0；u|z=Hb=uT,v|z=Hb=vT.其中Hb代表边界层的厚度,在本文中假设Hb=1500 m；(uT,vT)代表边界层顶部的风速,可由地转动量近似模型求得.本文在空间、时间方向上将方程(1)离散化,然后直接进行数值计算.

2.2 SGEM正模型求解

对于此随机模式的解法,本文拟采用混沌多项式展开的方法.根据Askey方案[16],若湍流黏性系数K的分布已知,其对应的最优混沌多项式基函数Ψ也就确定下来了.然后将输入随机变量K与输出随机量(u,v)在此基函数上展开,不同的是K的系数是已知的,而(u,v)的系数是需要求解的.所以问题由求解(u,v)的分布变为求解其多项式展开的系数.本文中采用回归法求解展开系数,此方法简单有效,易于理解,在使用较少计算资源的情况下也能有不错的效果.主要的思想就是对随机变量采样(样本数应该大于两倍的混沌多项式的项数)[17],然后计算得到解的样本集和多项式基函数的样本集,最后求解超定方程组,结果为多项式展开的系数.将SGEM模式记为U=g(K),输入随机变量K为湍流黏性系数,输出随机变量TΨi(ξ)为多项式基函数,ξ =[ξ1,ξ2,...,ξd]；P+1为多项式的个数,它与随机变量的维数d和截断的阶数r有关,即P+1=(d+r)!/(d!r!)[4].求解流程如图1所示.

3 逆模式及Kalman滤波类算法

若模式参数K是未知的,但我们可以根据专家猜值或者一些直接的但精度有限的观测得知其先验的概率密度函数p(K),风速U可以通过观测得到.为了降低参数的不确定性,得到一个更加接近真值的估计值,可以利用带误差的观测U∗.U∗=U+eU,误差eU符合另一概率密度函数.求解逆模式的目的就是估计出参数K在已知观测U∗的情况下的后验概率密度p(K|U∗).

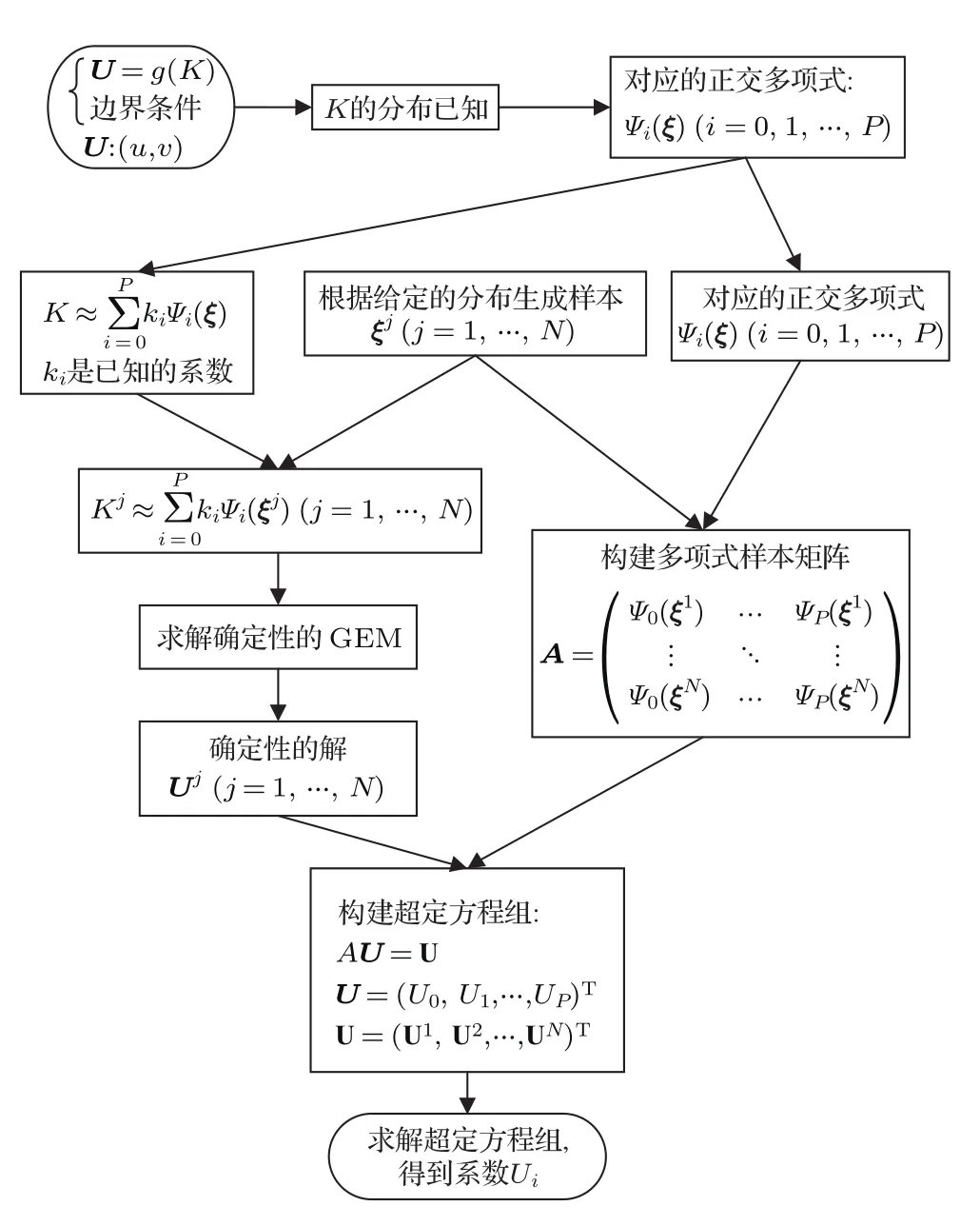
图1 SGEM预报模式求解流程图Fig.1.the flow chart for solving the SGEM.

3.1 Kalman滤波

Kalman滤波能给出准确的后验概率密度函数,但它有着较高的限制条件:1)模式必须是线性的；2)参数的先验密度函数p(K)与误差eU均服从正态分布.此时,参数的后验概率密度函数同样服从正态分布,其特征可以用均值µK|U∗与协方差CKK|U∗来表达.其求解过程如下.

第一步 预测,利用参数K先验分布通过线性随机模式求出输出量U的分布,又叫做预报模式求解过程.由于模式是线性的且均服从正态分布,所以很容易得到µU,CUU,CUK.µU代表U的先验/预测均值,CUK是U和K的先验协方差,CUU是向量U的先验/预测协方差.然后计算得到Kalman增益矩阵G.G=CKU(CUU+R)−1,式中,CKU=(CUK)T,R是误差eU的协方差矩阵,通常是预先给定的.

第二步 分析.通过观测值来调整参数K的分布,求出后验分布,具体来说就是求出后验均值与后验方差,可以通过下列公式得到:

其中µK和CKK分别代表参数K的先验的均值和协方差.

通常,观测数据是一个序列,所以Kalman滤波也会通过递归进行,每一个观测数据均会进行一次Kalman滤波过程.也就是说,根据前一次观测数据而求得后验分布会作为后一次Kalman滤波的先验分布.

3.2 EnKF

Kalman滤波方法只适用于线性模式,而大气海洋科学中大部分模式都是非线性的.对于非线性不太强的模式,我们可以用EnKF方法给出一个近似解,得出的后验分布不一定符合正态分布,但也是单峰型的,可以用前两阶矩(均值和方差)来表示其特征.对于非线性模式,通常采用蒙特卡罗法来求解输出变量的先验/预测分布,这就是EnKF.首先根据输入参数的先验分布采样,得到一组参数的样本集,然后对每一个样本进行确定预报模式的计算,得到输出变量的样本集.

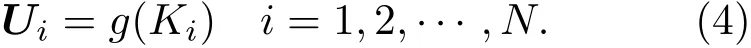
在输出变量样本集的基础上可以计算得到均值、协方差以及与输入参数的协方差.

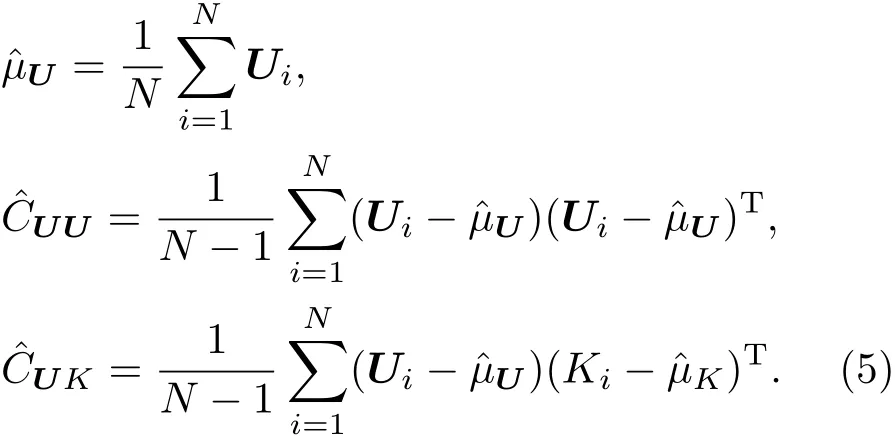
然后是分析步,由于是采样的方法,需要对每一个样本进行更新:

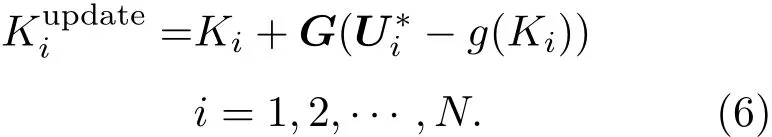
之后同样进行递归的过程.可以看到在(6)式中需要对观测U∗根据给定的协方差进行扰动后采样得到Ui∗,这就会产生不必要的采样误差.Whitaker和 Hamill[21]提出了集合均方根滤波方法(ensemble square root filter,EnSRF),此方法可以使用确定性的观测数据,这样就可以避免在观测时产生采样的误差.这种方法将参数K的均值和扰动分别进行更新.均值的更新使用标准的Kalman增益矩阵,而扰动的更新使用修正的增益矩阵:

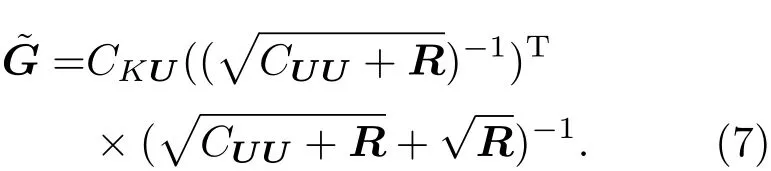
在本文中,我们EnSRF方法来进行反演的过程.

3.3 PC-EnKF

EnKF使用蒙特卡罗法进行输出变量的不确定量化,而蒙特卡罗法的收敛速度慢且需要足够大的样本来保证结果的准确性,这就造成了巨大的计算负担,特别是对于大型非线性模式.为了在不显著增加计算量的情况下增加逆模式的求解精度,本文采用EnKF的另外一个变种:基于混沌多项式的集合Kalman滤波方法(PC-EnKF).此方法类似于EnKF,只是在预报模式中采用混沌多项式展开来代替蒙特卡罗法进行不确定性量化.由于混沌多项式展开的关键在于多项式的系数,所以将EnKF中样本的更新改变为多项式系数的更新.具体实施步骤如下.

第一步 预测. 首先根据参数K的先验分布找出其最优的多项式基函数Ψi(ξ),ξ=[ξ1,ξ2,...,ξd]T是由一组给定的概率密度函数的相互独立的随机变量组成的,例如标准正态分布、均匀分布等.然后在此基函数上展开得到:由于其先验分布是已知的,所以系数ki也是已知的.然后利用上文说到的预报模式求解方法,求出中Ui是多项式展开系数.在本文中,假设参数服从正态分布,其对应的最优多项式为Hermite多项式[4,22].混沌多项式都有着标准正交的特性,E(Ψi(ξ)Ψj(ξ))= δij,δij是Kronecker delta函数.

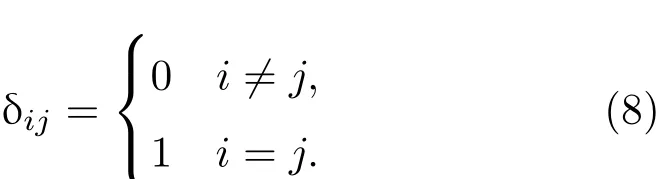
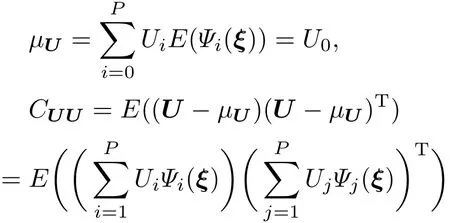
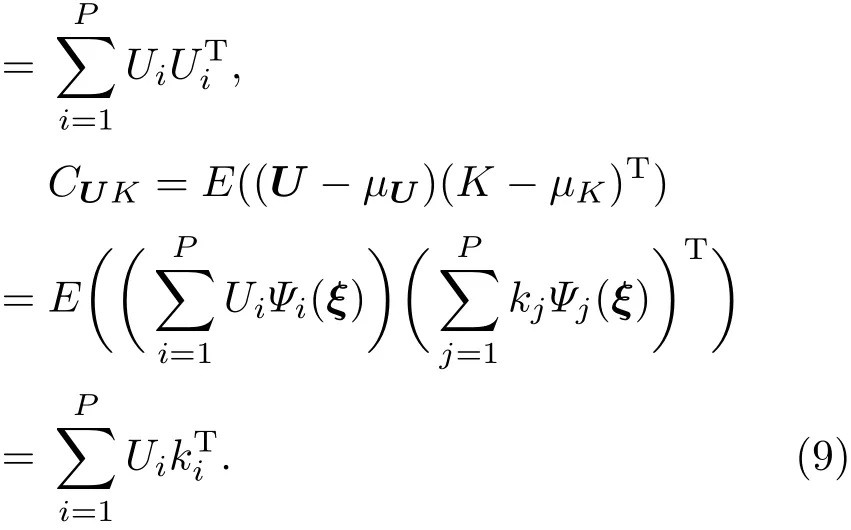
结合误差eU的协方差R,而且注意到CKU=(CUK)T,可以计算出Kalman增益和修正的增益.

第二步 分析.将观测数据同化进来,由此调整得到参数K的后验分布的多项式展开系数.本文中我们采用EnSRF策略进行更新,所以分为均值更新与扰动更新:

图2 利用PC-EnKF减少参数不确定性求解流程图Fig.2.the flow chart for reducing the uncertainty by PC-EnKF.

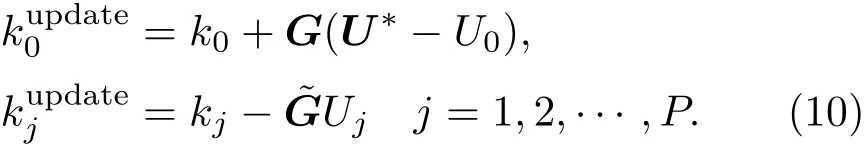
如有多次的观测,可利用递归的方式进行计算,根据前一次观测数据而求得后验分布会作为后一次Kalman滤波的先验分布.

后验分布的均值与方差容易求得:

其流程如图2所示.

4 数值实验

为了验证PC-EnKF在反演SGEM中湍流黏性系数K不确定性时的有效性.本文选取一类典型的气旋性地转切变流进行实验,其表达式为[2]:

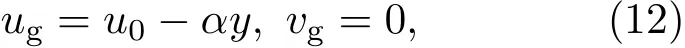
其中u0=20 m.s−1；α为常数,取α =0.4f,而f=10−4s−1.由于实际观测数据较难获得,本文决定采用模拟观测数据进行数值实验,在后续的研究中再使用实际观测数据.

我们假设反演两种类型下的湍流黏性系数；第一种,湍流黏性系数是常数,不随高度变化；第二种,湍流黏性系数是随高度变化的量.

何良诸打车，赶到北大坎市公安局。市局对姗姗来迟的何良诸，已经不感兴趣。矿工们上访、闹事，事出有因，领导一直下不了决心，执法部门不能动手。市局原定以倒卖稀世文物、查抄琥珀铭文为由，控制赵集、小勺等人。市局将方案报省后，既熟悉北大坎矿区，又是文物专家的何良诸被派下来。拦截国线火车的事件发生后，市领导抓住把柄，有胆量拍板了。那个晚上，警察出动，拘捕几个人，敲山震虎，天下太平了。

4.1 实验一

为了避免湍流黏性系数出现负值的情况,我们假设π=log(K),π服从正态分布.根据湍流黏性系数取值的大致范围确定先验分布π∼N(2,0.42),然后按照先验分布随机采样得到一个样本作为参考的真值参数,然后根据确定性的GEM模式计算得到相应的风速,在此基础上叠加符合正态分布的观测误差R∼N(0,0.22),N代表正态分布,各点的误差假定是相互独立的,由此生成模拟观测数据.观测数据随高度变化U∗(l)=U∗(zl),l=1,2,...,NH,NH为垂直方向格点数,在每个点上均进行一次Kalman滤波,这样就形成一个递归的过程.我们将垂直方向分成51个格点,这样就会有49个Kalman滤波过程(因为要去除两个固定边界条件).按照图2所示的流程图进行反演,为了直观地显示递归过程中的不确定性降低,每进行十六次循环,绘制一次模式输入量π和对应的模式输出量U的后验分布的均值和方差图形.

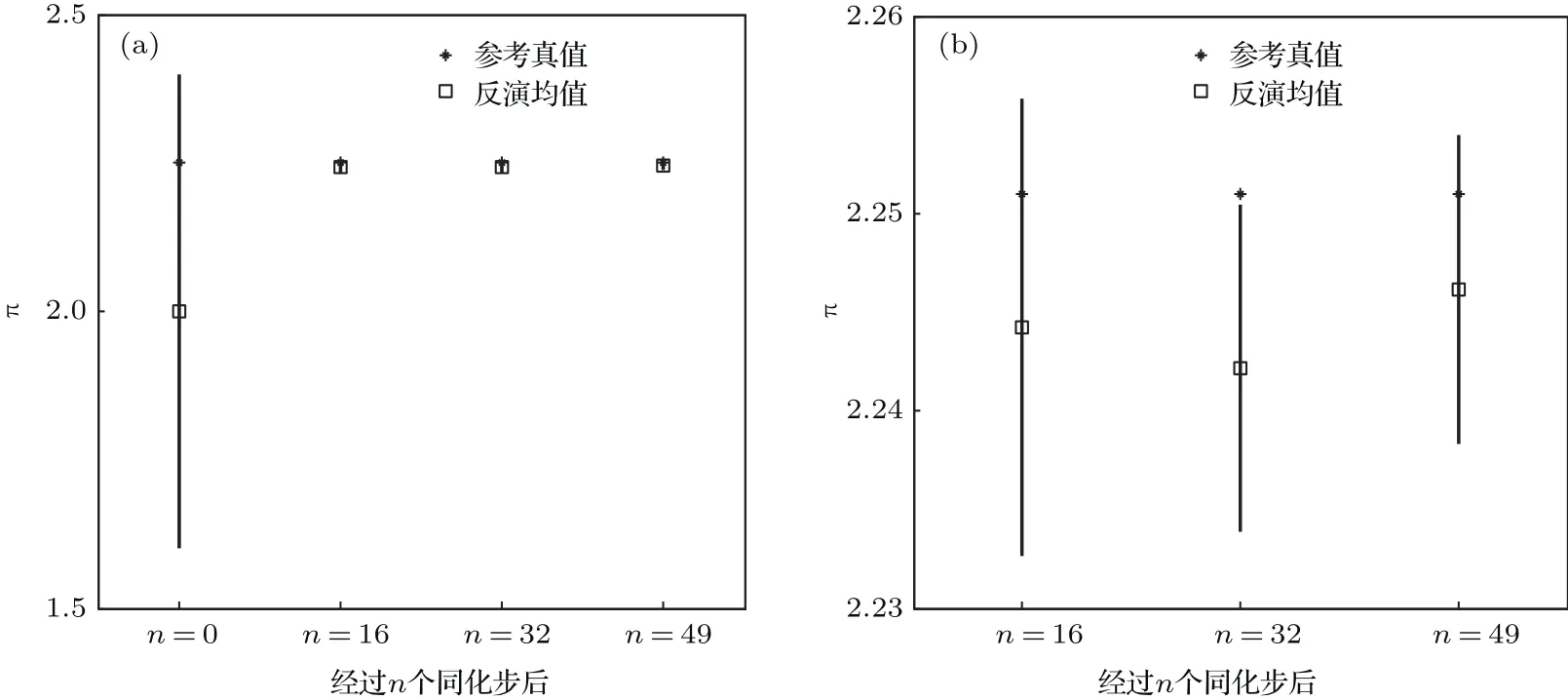
图3 模式参数π的置信区间(均值±标准差) 横坐标代表经过的迭代步数,0步代表并未经过同化的先验分布,其余为经过同化的后验分布；纵坐标代表π的取值；星号代表π的参考真值,方块代表π的后验分布的均值；注意:在(a)中,由于后验分布的不确定性很小,而(a)的纵坐标范围过大不能显示其中的细节,故将后验分布的置信区间放大放在(b)中Fig.3.The estimated confidence interval of model parameter π (mean ± standard deviation).The horizontal coordinate is the iterative number,where n=0 represents the prior distribution without assimilation,and the others are the posterior distribution after assimilation.The vertical coordinate is the value of π.The asterisk represents the reference value,the square represents the mean of posterior distribution.Note that the uncertainty of posterior distribution is small,while the range of vertical coordinate of Fig.(a)is too large to display details of posterior distribution.So,these details are shown in Fig.(b).

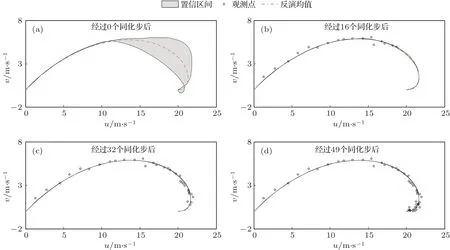
图4 风速Ekman螺线的观测数据以及风速分布示意图 灰色区域是分布的置信区间(均值±标准差),虚线代表Ekman螺线分布的均值,空心圆点代表观测点,也是数据同化点Fig.4.The wind observations of Ekman spirals and the distribution of wind.The grey shaded area is the confidence interval of wind speed(mean±standard deviation),the dotted line is the mean of wind distribution,the circular point is the observation point and also the data assimilation point.

从图3(a)可以看出,PC-EnKF能有效利用风速的观测信息进行反演,显著降低参数的不确定性.从图3(b)可以看出,随着同化过程的进行,参数不确定性在逐步减小且其后验分布的均值越来越靠近参考真值.

图4(a)中Ekman螺线先验分布的不确定性较大,在经过同化步后(图4(bd)),风速的不确定性明显降低,而且与观测数据的拟合程度较高,说明了PC-EnKF在降低参数不确定性方面是有效的.经过16个同化步之后预测的Ekman螺线与观测已经比较接近,也对应着图3(b)中经过16步的同化过程后模式参数的后验分布小的不确定性.

本文在风速先验分布中,不确定性较大的区域与不确定性小的区域各选取了10个观测点,在此基础上分别进行反演,比较其反演结果.

根据图5所示的观测点上的观测数据分别进行反演,可以分别求得两种观测下的参数后验分布.

从图6中可以明显地看出,相比于b区域,a区域观测的反演效果更好,均值更靠近参考真值且标准差更小.因为反演属于反问题,反问题的一个重要特点就是不稳定,不稳定即模式输出值小的变化就会引起参数的反演结果很大的误差,对应到不确定性分析中就是模式参数的先验分布不确定性较大,而对应的模式输出的先验分布不确定性较小.由一个小范围的分布去反演一个大范围的分布就会引起反演结果的不稳定.由此我们认为在模式参数先验分布不变的情况下,选取输出值先验分布不确定性较大的区域的观测进行反演会更加有效率,图6的结果也证明了我们的观点.这个发现对于风速观测点的位置的选择具有指导意义.

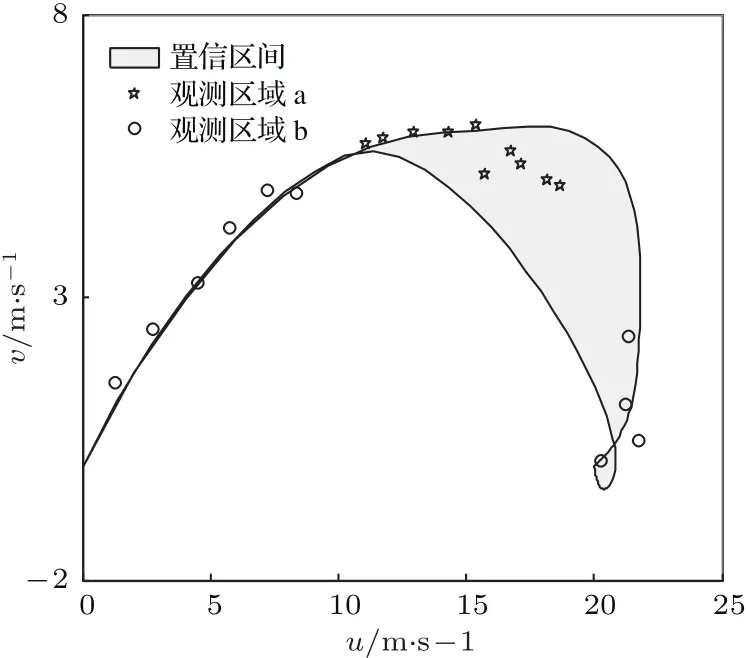
图5 选取的观测点示意图 灰色区域是风速先验分布的置信区间(均值±标准差),星号代表观测区域a(不确定性大的区域)的观测,圆圈代表观测区域b(不确定性小的区域)的观测Fig.5.The selected observation points.The grey shaded area is the confidence interval of wind speed(mean±standard deviation).The star represents observation in area a(heavy uncertainty),the circle represents observation in area b(small uncertainty).

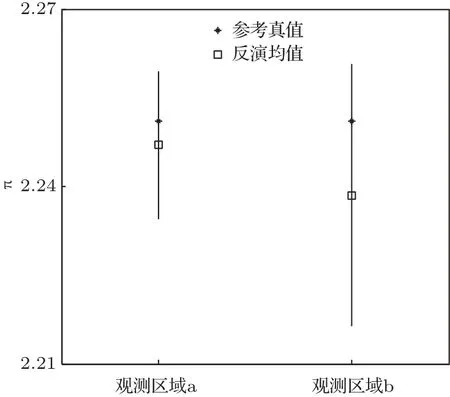
图6 由不同区域的观测反演的结果 横坐标代表不同的区域,纵坐标的模式参数π的取值,星号代表π的参考真值,方块代表π的后验分布的均值Fig.6.The result retrieved by different observations.The horizontal coordinate represents the area,the vertical coordinate is the value of π.The asterisk represents the reference,the square represents the mean of posterior distribution.

4.2 实验二

考虑湍流黏性系数一般是随高度变化的量,我们假设每个点的湍流黏性系数都是一个随机变量.因此系统成为高维的,混沌多项式的项数会急剧增加,计算量也会急剧增加.在本文中,我们假设垂直方向上格点的湍流黏性系数是存在相关性.K(z,ξ)是模式参数,假设其先验分布为对数正态分布,假设A=log(K),A符合正态分布,E(A)=2.08,Cov(A(z1),A(z2))=exp(−|z1−z2|/c),a=25,c=0.004. 我们在此基础上随机生成参考真值,然后经过确定性模式得到模式输出值,再加上符合观测误差协方差R∼N(0,0.22)的误差变成了带误差的观测值,N代表正态分布,且假设各点的观测误差独立.

在利用PC-EnKF进行反演之前,必须将模式参数A的先验分布表达成混沌多项式展开的形式,利用K-L分解(Karhunen-Loève expansion)[4],由于A的先验均值与协方差函数已知,可以将其近似表达为

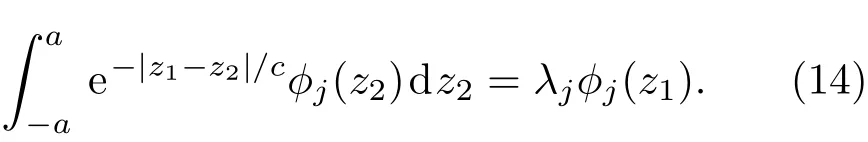
详细的步骤可以参阅文献[4,22].

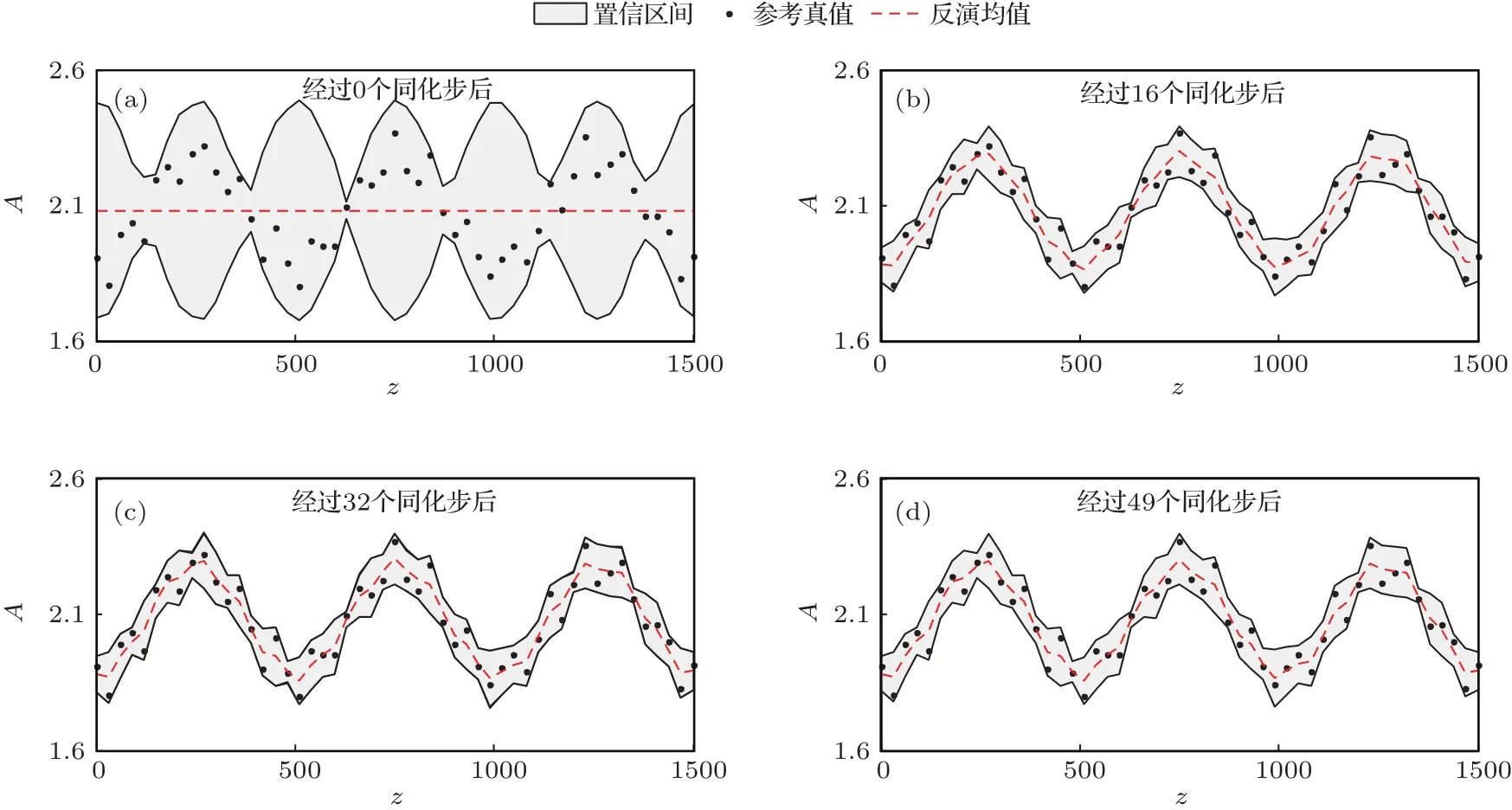
图7 模式参数A的分布示意 横坐标代表高度,纵坐标是参数的取值；灰色区域是分布的置信区间(均值±标准差),点代表模式参数A的参考真值,虚线代表的是分布的均值Fig.7.The distribution of model parameter A.The horizontal coordinate represents the height,the vertical coordinate is the value of model parameter.The grey shaded area is the confidence interval of A(mean±standard deviation),the solid point is the reference value of A,the dotted line is the mean of distribution.

图8 风速Ekman螺线的观测数据以及风速分布示意图 灰色区域是分布的置信区间(均值±标准差),虚线代表Ekman螺线分布的均值,空心圆点代表观测点,也是数据同化点Fig.8.The wind observations of Ekman spirals and the distribution of wind.The grey shaded area is the confidence interval of wind speed(mean±standard deviation),the dotted line is the mean of wind distribution,the circular point is the observation point and data assimilation point.

在得到先验分布的多项式展开之后,就可以实施PC-EnKF反演过程.与实验一类似,实验二同样是每隔16次绘制一次模式输入量π和对应的模式输出量U的后验分布的均值和方差的图形.

从图7(a)可以看出参数的先验分布不确定性是相当大的,参考真值与分布的均值相去甚远.经过同化过程后,不确定性有了明显的减小,特别是均值与参考真值已经很接近了.

图8(a)中Ekman螺线先验分布的不确定性不是很大.在经过同化步后(图8(b)—(d)),Ekman螺线的不确定性有所降低,与观测数据的拟合程度高,说明了PC-EnKF在降低参数不确定性方面是有效的.在实验二中我们同样选取了不确定性大与不确定性小两个区域的观测,并分别进行反演.观测点的位置如图9所示.

可以很明显地看出,图10(a)中的反演效果更好,具有更小的不确定性,进一步缩小了参数分布的区间.这也佐证了我们的观点,在不确定性大的区域的观测数据在反演时具有更好的效果.而且实验二中风速的先验分布(图9)的不确定性明显比实验一(图5)的小,根据我们上文中的分析,实验二中模式参数的反演的不稳定性更强,反演难度大于实验一.比较图7与图3,可以看出实验二的反演结果也较实验一差.

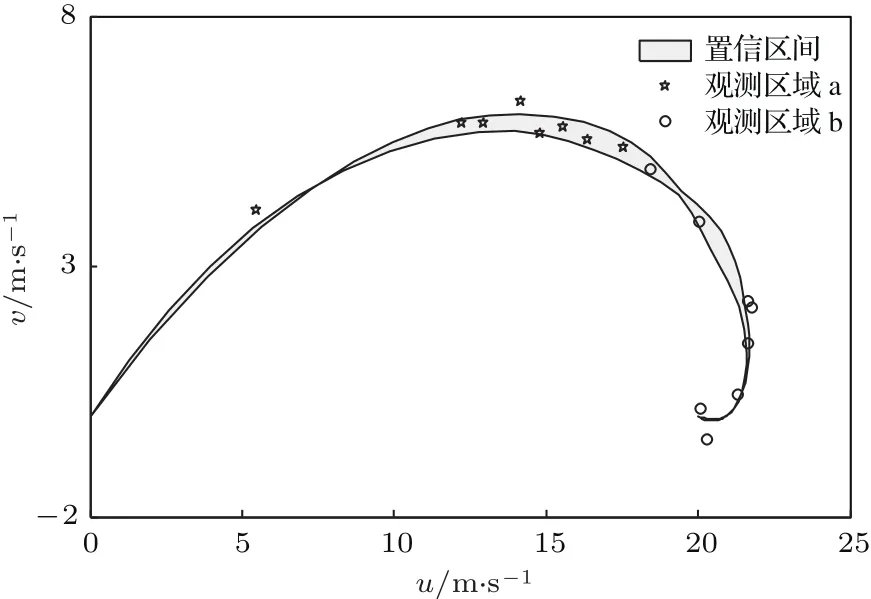
图9 选取的观测点示意图 灰色区域是风速先验分布的置信区间(均值±标准差).星号代表观测区域a(不确定性大的区域)的观测,圆圈代表观测区域b(不确定性小的区域)的观测Fig.9.The selected observation points.The grey shaded area is the confidence interval of wind speed(mean±standard deviation).The star represents observation in area a(heavy uncertainty),the circle represents observation in area b(small uncertainty).

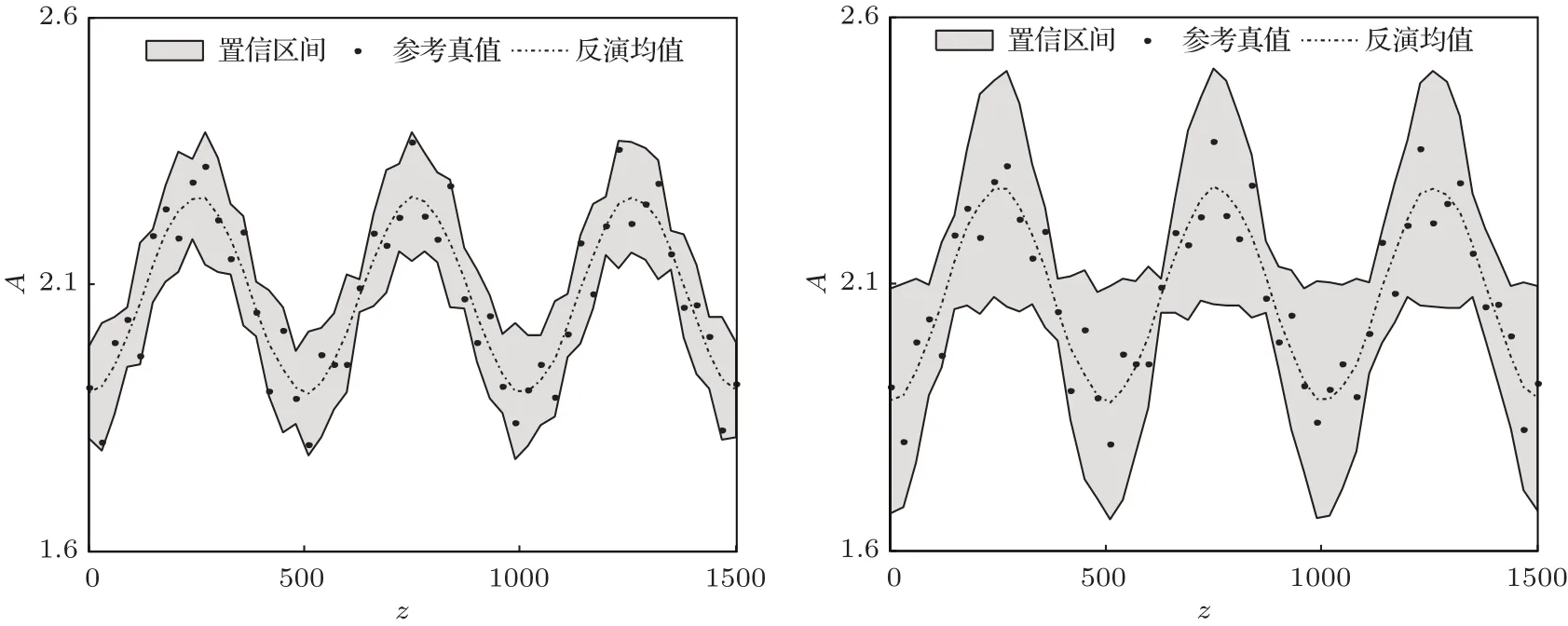
图10 由不同区域观测反演参数A的结果 横坐标代表高度,纵坐标是参数的取值,灰色区域是分布的置信区间(均值±标准差),点代表模式参数A的参考真值,虚线代表的是分布的均值；(a)代表由观测区域a中的观测反演的结果；(b)代表由观测区域b中的观测反演的结果Fig.10.The result retrieved by different observations.The horizontal coordinate represents the height,the vertical coordinate is the value of model parameter.The grey shaded area is the confidence interval of A(mean±standard deviation),the solid point is the reference of A,the dotted line is the mean of distribution.(a)display the result retrieved by observations in area a,(b)display the result retrieved by observations in area b.

5 总结与讨论

本文利用PC-EnKF方法以及风速的观测,对SGEM模式中湍流黏性系数的不确定性进行了反演,求出了其后验概率密度函数.采用两类不同类型的湍流黏性系数进行数值实验,实验一中假定待反演的系数是常数,实验二中假定是符合先验协方差函数的随高度变化的系数,均采用PC-EnKF进行反演.实验结果表明,PC-EnKF能够很有效地求解后验概率密度函数,混沌多项式展开能够有效进行不确定性的表达,将PC与EnKF结合起来能够用于不确定性的反问题.而且我们在实验中发现,根据系数的先验分布计算出风速的先验分布,在此基础上找到风速不确定性大的区域,在此区域内的观测数据在反演系数时具有更好的效果,这对于观测点的位置的选择具有指导意义.

本文利用混沌多项式展开的方法代替EnKF中的蒙特卡罗法,能够很有效地进行不确定性问题的反问题.但是由于混沌多项式展开对于高维的不确定性问题的计算量急剧增加,所以PC-EnKF对于高维问题的求解还存在着一些问题,下一步的工作中将重点关注不确定性降维方面.