基于区域密度曲线识别网络上的多影响力节点∗

康玲 项冰冰 翟素兰 鲍中奎 张海峰

(安徽大学数学科学学院,合肥 230601)

(2018年5月23日收到；2018年6月27日收到修改稿)

1 引 言

随着信息技术的发展以及经济的全球化,人类的社会活动日趋网络化,像在线社交网络、科研合作网络、交通网络、电力网络以及与人自身相关的新陈代谢网络等不断进入人们的视野.另外,这些网络的数据规模与日剧增,内在结构也变得日益复杂.面对这些大规模的复杂网络,能否有效识别其中具有影响力的节点,具有重要的理论意义和实际应用价值,已被广泛应用于疾病传播、谣言扩散、新产品的推广以及交通拥堵的治理等方面[1−6].

一些中心性指标如度中心性[7]、介数中心性[8]、接近中心性[9]、特征向量中心性[10],k-shell分解等[11]相继被提出来识别网络中的影响力节点.近年来,Chen等[12]考虑了节点的高阶邻居信息,提出一种基于多级邻居信息的半局部指标来进行节点的排序；考虑到网络的结构洞节点对网络传播的作用,韩忠明等[13]以及苏晓萍和宋玉蓉[14]结合结构洞理论,利用邻域的结构洞来探测网络中的最具影响力节点；Radicchi和Castellano[15]提出非回溯性指标并结合渗流理论来进行关键节点的识别.由于信息在网络中的传播,不仅与节点间的最短路径有关,还与节点间最短路径的条数以及传播率有关.阮逸润等[16]在文献[17]的基础上提出一种改进的SP(传播概率)指标来评估节点的影响力.然而,以上对影响力节点的研究主要基于单个影响力节点来开展,但事实往往并非如此,像一些疾病、谣言或广告的传播可能来自多个不同的传播源,所以网络中往往存在多个影响力节点.Hu等[18]在带有社团结构的网络中探讨了多影响力节点的识别问题,并发现每个社团的hub点(大度节点)往往具有很强的传播能力.然而,当传播源的个数超过社团数目时,该方法将无能为力.Zhao等[19]将图论中的着色方法引入复杂网络中,提出一种多影响力节点的识别方法,但该方法有时不能保证传播源间的分布足够分散；Guo等[20]提出了改进的着色方法.可以看出,对复杂网络影响力节点的识别研究还处于初始阶段,仍有许多问题有待进一步改进.

多影响力节点识别的指导性思想是:选取的节点间的分布要较为分散,且自身要足够重要,这样能在保证传播非冗余的同时,使得传播范围尽可能的广.但两者之间要想同时满足几乎不可能,只能在两者之间寻求一个平衡.在网络的核心-边缘(core-periphery)和社团结构探测中,我们提出一种统一的方法,即通过绘制网络的区域密度曲线(region density curve),然后利用曲线的峰值点来确定网络的核(core)节点或者社团内部的节点,进而用局部扩张的方法来获得网络的核心边缘(coreperiphery)结构和社团结构[21].通过对网络区域密度曲线的进一步分析,发现区域密度曲线的波谷点正是连接核心与边缘(core-periphery)、或者社团和社团之间的桥梁节点.与其他节点相比,桥梁节点在网络的传播过程中具有很重要的影响力[22],并且分布较为分散.鉴于此,本文提出基于区域密度曲线的多影响力节点识别方法(RDC),并在不同的网络上利用疾病和谣言两种不同的传播模型进行了实验分析,结果表明,RDC能够很好地识别网络中的多影响力节点,而且能够保证选取的这些影响力节点之间分布较为分散,自身也足够重要.

2 方 法

假设网络是一个无权无向图G(V,E),其中V表示网络中的节点,E表示网络中的连边.首先,给出几种常用的中心性指标,本文将以这些作为所提方法的比较指标.

2.1 中心性指标

度中心性(DC),被定义为节点的邻居数目,即

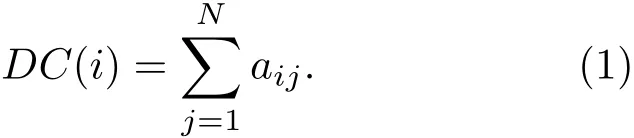
介数中心性(BC),是以经过某个节点的最短路径的数目来刻画节点的重要性指标,即

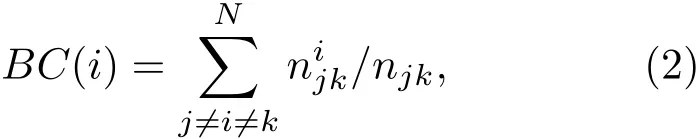
其中,njk为从节点j到节点k的最短路径的数目,n为从节点j到节点k的条最短路径中经过节点i的最短路径的数目.

k-shell方法(KS)的具体步骤如下:首先把网络中度为1的节点及其所连接的边去掉,剩下的网络中会出现一些度为1的节点,再将这些度为1的节点去掉,直到所剩的网络中没有度为1的节点,则所有被去掉的节点称为1-shell；然后继续上面的方法,去掉剩下的网络中度为2的节点及其相连的边,直至不再有度值为2的节点为止,则这一轮所有被去除的节点及其连边称为网络的2-shell.依次类推,直到所有的节点都被分到相应的k-shell.

度折扣方法(DDC)是由Chen等[23]提出的,其思想是:设v是节点u的邻居集,如果u已被选作传播源,当基于度中心性考虑v作为下一个传播源时,为避免传播冗余,我们不应该再考虑uv的边,应对v的度进行折扣减1.

将图论中的图着色方法引入复杂网络,Zhao等[19]使用Welsh-Powell算法将网络分成若干个独立的子集,以保证每一个独立子集中的任意两点都不相连.然后基于某个中心性指标,在最大的独立子集中选取按指定的中心性指标排序靠前的m个节点作为多传播源.在文中,我们比较了基于度中心性、介数中心性以及k-shell中心性等着色方法,分别标记为DCC,BCC和KSC.

2.2 基于区域密度曲线的多影响力节点探测

首先对网络中的节点进行重新排序,使连接紧密的节点的次序也相近；然后绘制网络的区域密度曲线,并找出曲线上的波谷点；最后在波谷点两侧选取一定比例的节点作为影响力节点,具体步骤如下[21].

1)对节点进行排序,使连接紧密的节点次序也相近

定义一个初始集合U=ϕ,初始化V′=V.U作为存储有序序列,V′=V/U为待选集合.首先,从V中选择一个中心性指标比较好的节点N2加入到序列U中；然后,计算V′中各节点的C(i,U)值,C(i,U)值最大的节点作为节点序列的第二个节点N2,即选择与U中节点的连接的数量最多的节点加入到U中.若同时找到两个或两个以上的节点,选择度大的节点添加到U中；更新V′和U,按照上面的方法依次进行,最后可得U={u1,u2,...,uN},V′=ϕ.

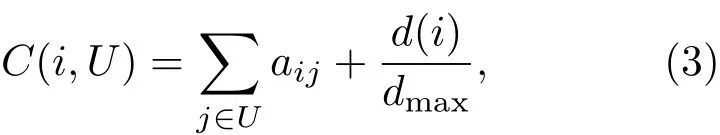
其中,aij表示节点i与j是否相连,如果相连aij=1,否则aij=0；d(i)是节点i的度,dmax是网络中最大度节点的度.

2)绘制网络的区域密度曲线

为了刻画网络中某个区域S内部点的连接密度,定义S的区域密度CD(S)为

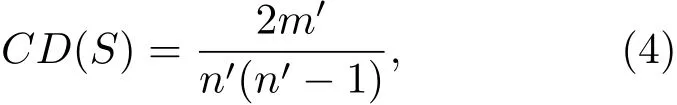
其中n′为区域S内节点的数量,m′为区域S内连接的边的数量.

给定参数值α,即核的最小尺寸,在文中取作网络的平均度.在节点序列U中,将排序为r的节点Ur的区域密度定义为序号为r−α−1至r的节点组成的子图的区域密度,即

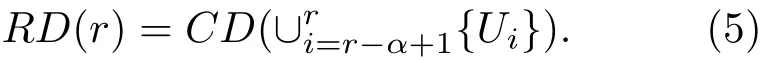
然后,将各节点的区域密度绘制在二维直角坐标系中,即获得网络的区域密度曲线(密度曲线如图1(a)所示).在文献[21]中,通过对该区域密度曲线的分析可以探测出核心-边缘(core-periphery)结构、社团结构等,而且可以找出连接不同社团之间的桥粱节点.基此,我们利用此方法来探测网络中的多影响力节点.

3)多影响力节点的选取

首先,通过上面绘制的区域密度曲线,找出处在波谷位置的节点.注意到区域密度曲线的第1个节点的RD值为0,第2个会达到峰值(因为两个节点有连接就是全连接),故第一个节点的RD值不是有效值.另外,区域密度曲线的末端代表的都是些比较稀疏的节点,与社团以及核心边缘结构等没有多大的联系,因此选择多传播源时,不考虑区域密度曲线这两个波谷位置的节点.

然后,利用区域密度曲线,计算出各谷点之间的节点数,并确定各谷点处要选取的传播源的个数.假设要求探测m个有影响力的节点,通过区域密度曲线观测到波谷位置的节点序号为[N0,N1,...,Nk,Nk+1](其中N0和Nk+1为上面讨论的两类节点),同时记录每个节点之间的节点数[n1,n2,...,nk+1](其中ni(i=1,2,...,k)代表Ni和Ni+1之间的节点数,如下例中图1(a)标注的n4),则在各个谷点处选取传播源个数为[m1,m2,...,mk], 其中第i(i=1,2,...,k)个谷点Ni处的传播源个数mi定义为

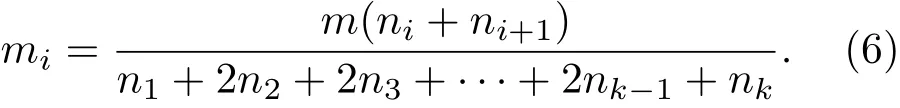
因为我们是从谷点Ni所在位置的两边选取一定比例的传播源,所以分母会出现系数2,相当于 (n1+n2)+ (n2+n3)+...+ (nk−2+nk−1) + (nk−1+nk).

最后,在各个谷点位置的左右两边各选取一半比例的传播源,利用各谷点确定的传播源放在一起,即是要探测的多传播.具体算法如下.

算法1 节点进行排序

输入:网络G(V,E).

输出:节点排序U(有序集合).

1)初始化:U=∅,V′=V.

2)选择最大接近中心性节点N2,U← N2,V′=V′/N2.

3)WHILE V′̸= ∅DO.

4)FOR i∈Γ(U)∪V′DO.

5)通过(1)式计算C(i,U).

6)N2=argmax(C(i,U))(若存在多个最大

i值,取度最大的节点)

7)ENDFOR.

8)U ← N2,V′=V′/N2.

9)ENDWHILE.

算法2 寻找多个影响力节点

输入:节点排序U多影响力节点的个数K.

输出:多影响力节点的集合C.

1)初始化C=∅.

2)FOR Ui∈U DO.

3)通过(3)式计算RD(i).

4)ENDFOR.

5)计算RD曲线的有效谷点序号为:[N0,N1,...,Nk,Nk+1](其中N0和Nk+1为文中讨论的两类节点).

6)统计谷点之间的节点数:[n1,n2,...,nk+1].

7)通过(4)式计算每个谷点处要寻找的影响力节点的个数[m1,m2,...,mk].

8)FORi∈ [1,...,K]DO.

9)在Ni谷点处前后共取Mi个节点记为Ci.

10)C=C∪Ci.

11)ENDFOR.

其中Γ(U)表示U中所有节点的邻居.下文中用RDC来表示本文提出的方法.

下面以Football网[24]为例来说明具体的探测方法,假设要探测的传播源的个数m=12.首先利用(1)式,对网络节点进行重新编号,并利用(2)式和(3)式,计算每个节点的区域密度.然后,以横坐标为节点序列,纵坐标为区域密度,绘制出节点区域密度曲线图,如图1(a)所示.接下来,寻找区域密度曲线的谷点,得到谷点的节点序列[1,77,89,115,4,36,65,22,13,43],记录各谷点之间的节点数目,记为[15,15,15,17,14,9,9,13,8]；然后,根据(4)式计算各谷点处应该选取的传播源个数,记为[2,2,2,2,1,1,1,1]；最后,在每个谷点的左右两边各取一半的传播源,比如在第一个谷点77号的前面选取1个,那么在77号的后面选0个传播源,因为谷点本身就已经作为传播源了,以此类推,最终选取12个传播源[96,77,37,89,84,115,85,4,36,65,22,13].图1(c)所示为选取的影响力节点及其位置情况,其中红色圆圈代表的节点就是我们找到的12个传播源,可以看出,这些节点并不是所谓的大度节点,恰恰相反的是,有些节点的度却很小,比如图中的37号,13号以及96号节点,但这些节点往往都位于不同社团的交界处.这也正好满足我们所寻找传播源的条件,传播源之间能尽可能的分散,避免传播的冗余.

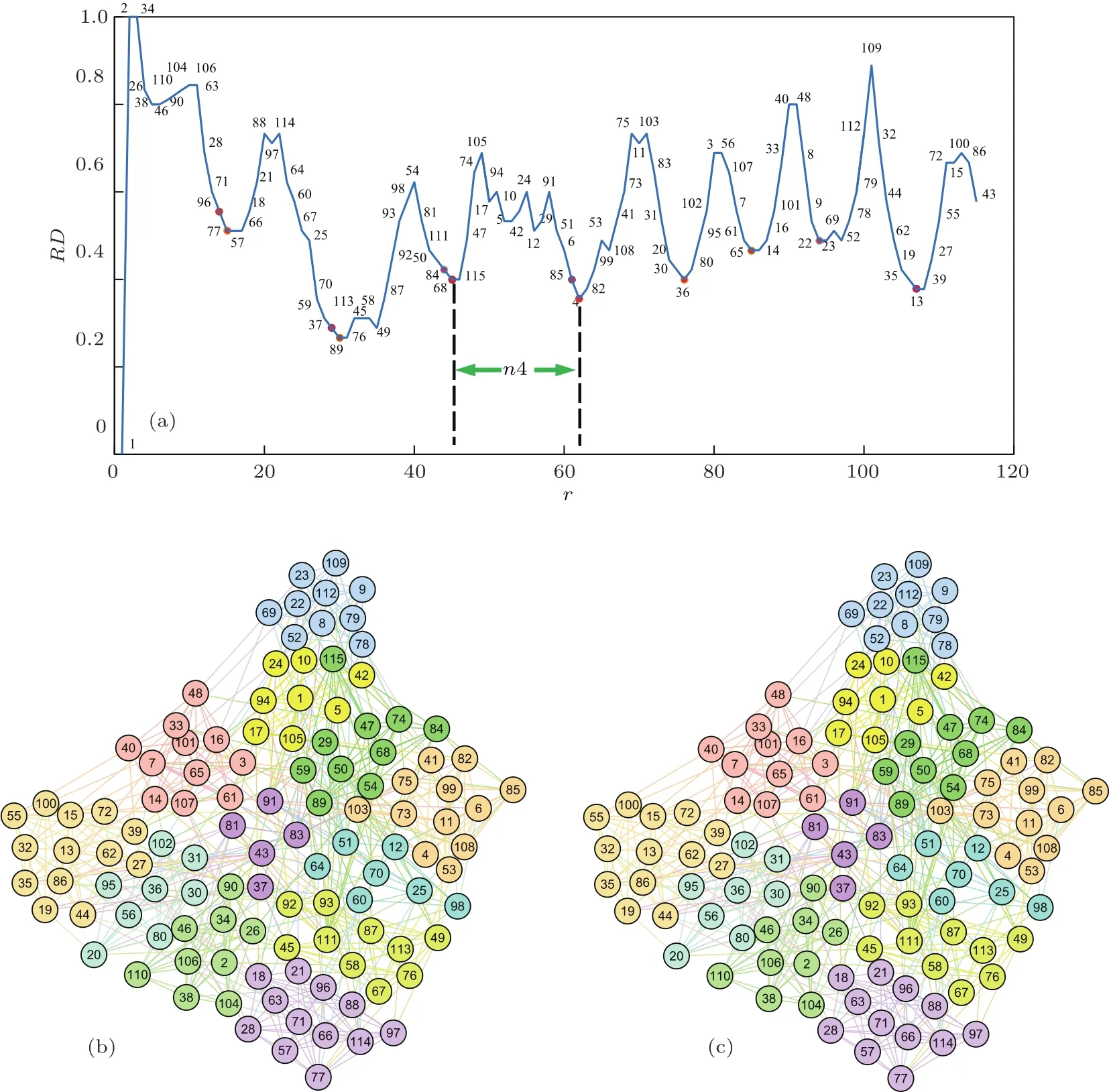
图1 Football网的多影响力节点识别 (a)网络的区域密度曲线；(b)网络的划分情况,不同颜色代表不同的社团；(c)红色的节点为RDC方法选取的12个影响力节点Fig.1.Identification of multiple influential nodes on the football network:(a)Region density curve of the network；(b)original structure,where nodes with the same color are in the same community；(c)the twelve red nodes are influential nodes which are identified by the RDC method.

3 实验分析

3.1 传播模型

很多文献中已经指出,节点的影响力是依赖于传播的动力学[25,26].因此,在本文分别考虑两种疾病传播动力学,疾病传播的SIR模型和谣言传播模型,进而更全面地来比较不同传播源探测方法.

在疾病传播模型中,网络中的节点分为三类,易感者(S),感染者(I),恢复者(R).一个感染者(I)以一定的传播率将疾病传染给易感的邻居(S),传播完自己的所有邻居后,感染者以一定的恢复率变为恢复者[27].在这里,为了更清晰地区分不同的传播源探测方法,仅考虑每个感染者每次仅与一个邻居接触,即单传的SIR模型.

在谣言传播模型中,将网络节点分为三类,无知者(S),传播者(I),已知者(R).一个传播者(I)以一定的概率将谣言传播给相邻的无知者(S),当传播者接触到另一个传播者或已知者时,最初的传播者就会失去传播谣言的兴趣,以一定的概率变为已知者[28].本文考虑恢复率µ=0.1的情况.

3.2 数据描述

将不同的多影响力节点识别方法在六个真实网络中进行比较,包括Email,Yeast,SciMet,Kohonen,HEP,PGP.表1是网络的一些基本信息,其中N,M为网络的节点数和边数,⟨k⟩和C为网络的平均度和聚类系数,L和D为网络的平均短路径长度和直径[29].

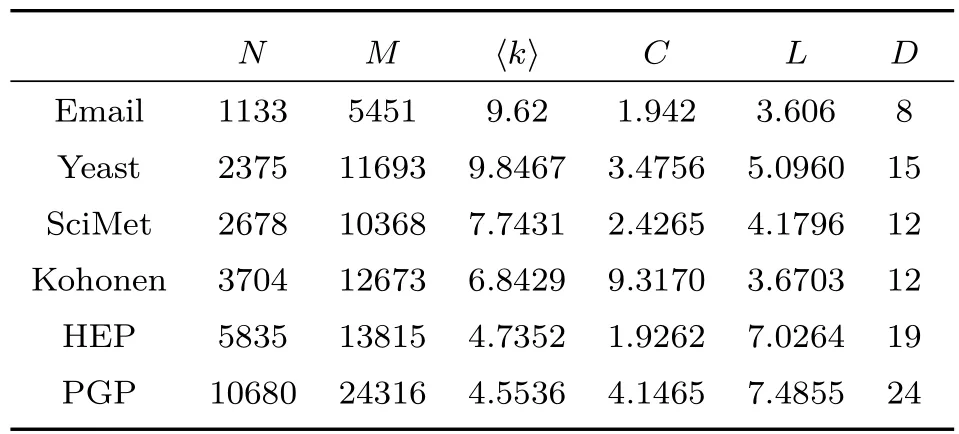
表1 网络的基本信息表Fig.1.Basic structural properties for networks.

3.3 结 果

为便于比较不同的多影响力节点识别方法,首先选取m个传播源,然后分别依据SIR疾病传播、遥言传播模型,去模拟网络的动力学过程,直到网络中没有处于感染态的节点,最后以网络中恢复节点的比例来衡量识别方法的性能.为了保证实验结果的可靠性,对传播过程文中进行了100次平均.

为便于比较不同方法的结果,定义一个相对比率指标∆如下[19]:

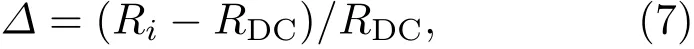
其中,Ri表示在某种传播源识别方法(如DCC,KS,KSC,BC,BCC,DDC,RDC)下最终恢复节点的比例,RDC是采用度中心性方法时最终恢复节点的比例.∆＞0意味着当前使用的方法要优于度中心性的方法,∆＞0的值越大表示当前方法的优势越明显.

首先,利用SIR疾病传播模型,在六个实际网络上对不同的识别方法进行比较.实验结果表明,面对SIR疾病传播时,本文提出的基于区域密度曲线的识别方法(RDC)都要优于其他方法,尤其是当传播率较小时,优势非常明显.即使传播率增大到一定程度,RDC方法还是要优于其他方法.另外,随着选取的传播源个数的增多,这种优势越发明显(见图2和图3).图2是在SIR疾病传播模型下,不同识别方法相对于度中心性指标所得的结果,其中传播率β从0.05到0.5,每次增加0.05,恢复率µ=0.1. 图2(a)—(f),(g)—(l),(m)—(r)表示传播过程中选取的传播源个数分别为30,50,90.

紧接着,在上面的六个实际网络上,考虑了不同识别方法在谣言传播模型中的效果.实验结果表明,在谣言传播机理下,RDC方法仍然要优于其他的多影响力节点识别方法.随着选取的传播源个数的增加,RDC方法的优势越发明显.图3是在谣言传播模型下的实验结果,参数的设定与SIR疾病传播模型下的相同.图3(a)—(f),(g)—(l),(m)—(r)表示传播过程中选取的传播源个数分别为30,50,90.

接下来,研究不同识别方法所得的影响力节点之间的平均距离和平均度的情况.图4是考虑不同识别方法所获取的影响力节点之间的平均距离随传播源个数的变化情况,其中传播源的个数m是从20开始,每次增加20,一直到200.可以看出,相比较于其他识别方法,利用RDC方法选取的传播源之间的平均距离要大很多,并随选取的传播源个数的增加,平均距离呈现增大的趋势.由此可以看出,RDC方法获取的传播源彼此之间较为分散,能够很好地避免传播的冗余.

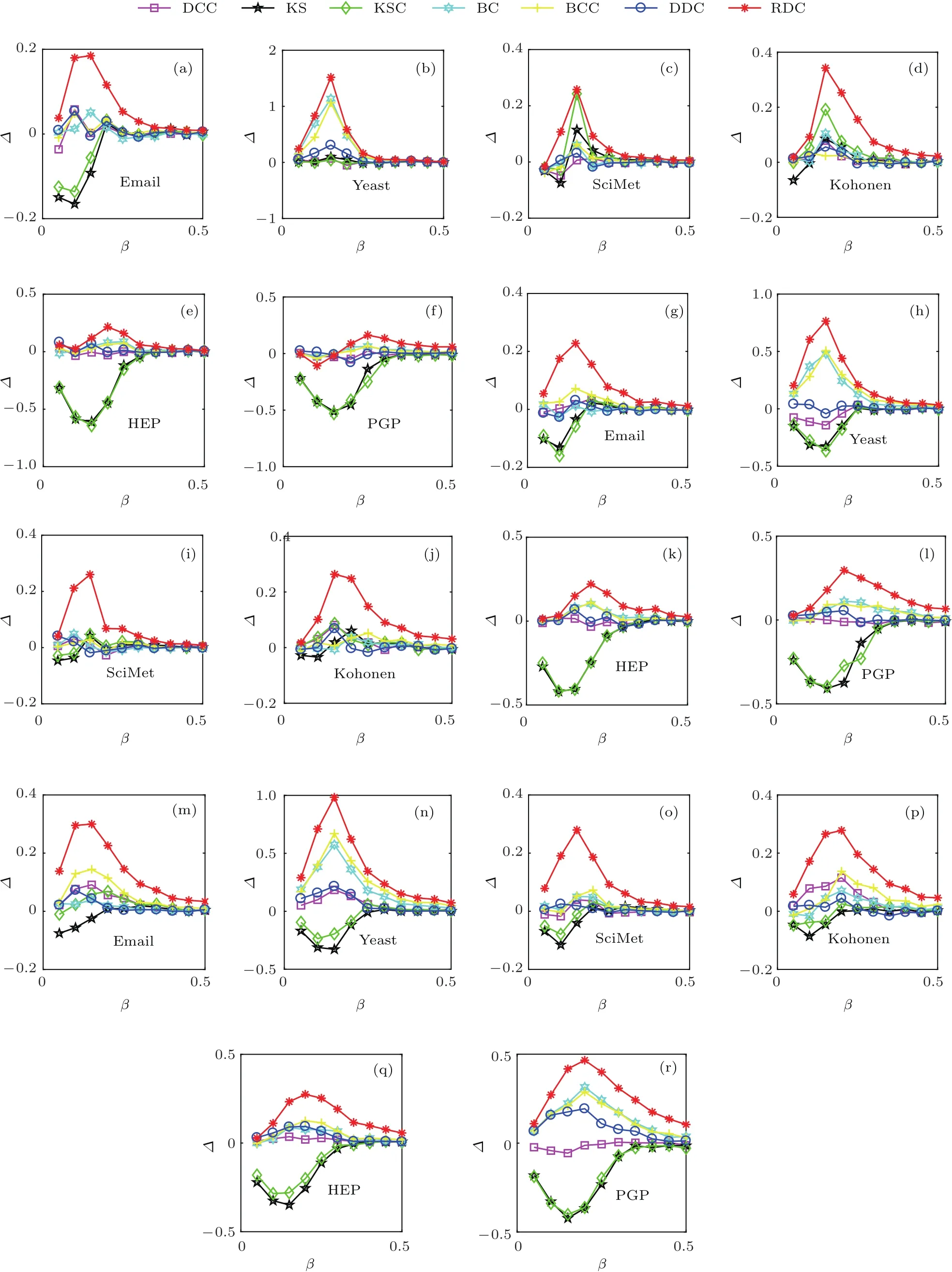
图2 对于SIR疾病传播模型,不同识别方法与疾病传播率之间的关系Fig.2.For SIR model,the relative ratios∆ for different indices as functions of transmission rate β are compared in six real networks.

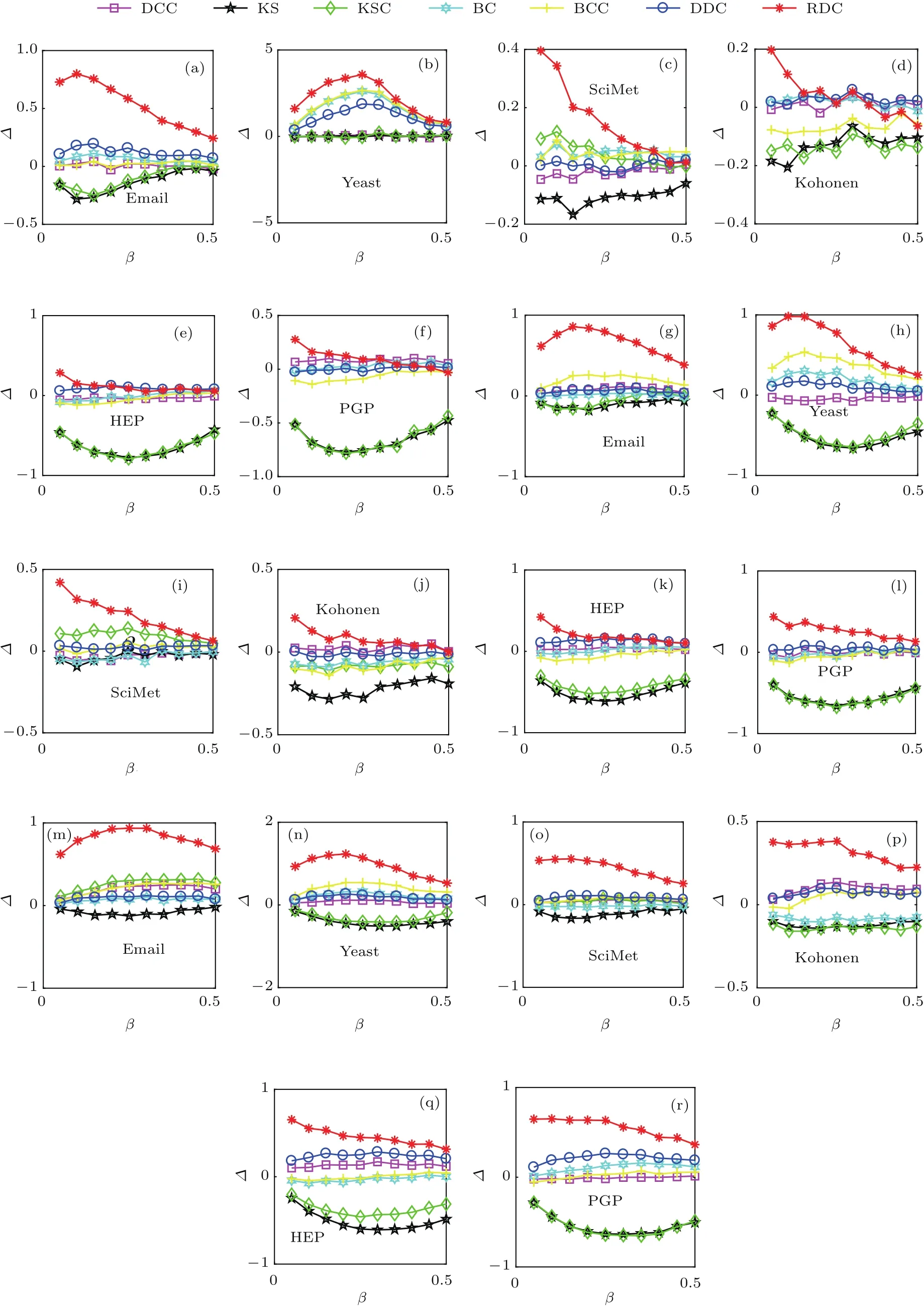
图3 对于谣言传播模型,不同识别方法与疾病传播率之间的关系Fig.3.For rumor propagation model,the relative ratios ∆ for different indices as functions of transmission rate β are compared in six real networks.

图5是不同识别方法所获取的影响力节点的平均度随传播源个数的变化情况,其中传播源个数m的设定与图4相同.可以看出,RDC方法选取的传播源的平均度要小于其他的识别方法.由选取传播源的指导思想可知,传播源间的分布分散和自身重要两者不可兼得.虽然RDC方法选取的传播源的平均度比其他方法都要小,但从图5中的蓝色虚直线(即网络的平均度)可以看出,选择的这些传播源不是“不重要”的节点,这些节点的平均度比各自网络的平均度都要大.而且随着选取的传播源个数的增加,RDC方法的平均度基本保持不变.由此可以看出,RDC方法选取的传播源彼此间分布较分散,而且各个传播源自身也比较重要.

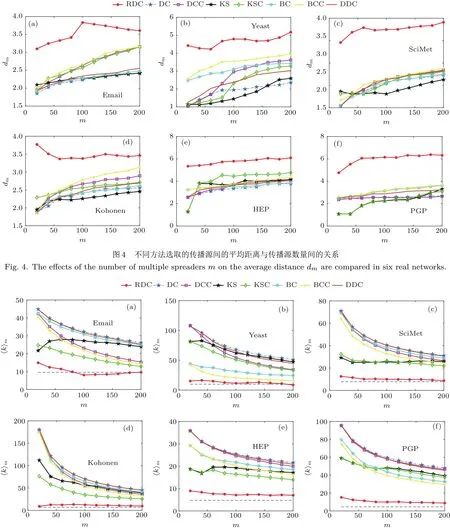
图5 不同方法选取的传播源的平均度与传播源数量间的关系,其中蓝色虚线代表每个网络的平均度Fig.5.The effects of the number of multiple spreaders m on the average degree ⟨k⟩mare compared in six real networks.Dotted line in each subfigure denotes the average degree of the network.

图6和图7讨论了不同的参数α对传播模型的影响,红色方框中的部分是本文采用的α值,可以发现随着α的变化,传播范围会呈现一定的无规则的波动.因此本文采用了文献[21]提供的默认参数平均度,虽然不是在所有的网络都是最优的,但是总体表现较好.

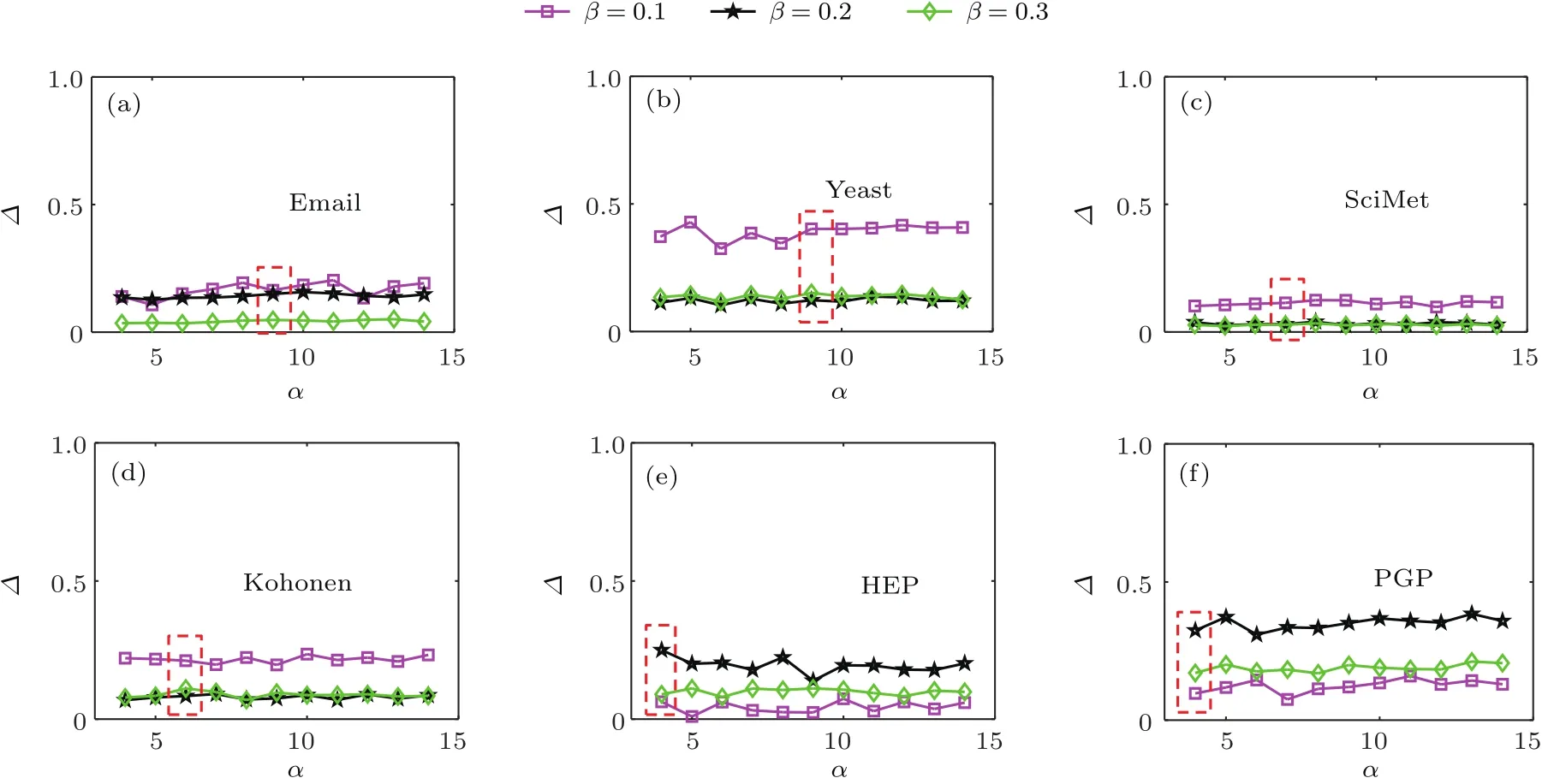
图6 对于SIR传播模型,不同传播率下参数α与相对比率∆的关系Fig.6.For SIR model,the effects of parameter α on the relative ratios ∆ for different transmission rates β are compared in six real networks.

图7 对于谣言传播模型,不同传播率下参数α与相对比率∆的关系Fig.7.For rumor propagation model,the effects of parameter α on the relative ratios∆ for different transmission rates β are compared in six real networks.

4 结 论

多影响力节点识别的指导性思想是:选取的节点彼此间的分布要较为分散,而且自身要足够重要,但两者不可兼得.本文提出一种基于网络区域密度曲线的多影响力节点识别方法,该方法基于网络的局部信息,计算的时间复杂度较低.应用两种不同的传播动力学模型,在六个真实网络上进行了数据实验,结果表明本文提出的识别方法要优于其他的识别方法,而且选中的影响力节点之间的分布较为分散,自身也较为重要.本文仅考虑无向无权网络,下一步可考虑将本文的方法推广至有向有权网络中.