带有控制增益自校正的甚低轨道卫星自主轨道维持方法

谢 挺，刘 刚，高旭东

(1.上海卫星工程研究所，上海 201109； 2. 上海航天控制技术研究所， 上海 201109)

0 引言

一般来说，工程上实用的甚低轨道高度约为300～450 km。甚低轨道卫星的主要特点为：1)实现高分辨率对地观测，对遥感仪器而言，选择更低的轨道，可有效提高地面图像分辨率，获取更好的观测效果；2)有效降低发射成本，在运载能力相同的情况下，采用的轨道更低，耗费较低；3)甚低轨道上受到的气动力比传统低轨卫星高，大气密度为10-12～10-10kg/m3，对轨道高度有较大影响。故需要设计合理的轨道维持方案，对轨道高度进行频繁控制，实现甚低轨道的长期稳定运行[1]。

从工程实现的角度来看，甚低轨道卫星主要运行在近圆轨道上，因此可直接根据二体问题中的航天器轨道动力学方程[2-3]，得到低轨近圆轨道高度变化的模型及卫星变轨时由轨道参数变化量到轨道控制量之间的简化计算公式。目前对于甚低轨道的轨道控制方式主要有气动力控制和喷气主动控制[4]。由于甚低轨道大气阻力影响明显，需要频繁进行轨道控制才能维持一定的轨道高度，因此采用气动力控制能有效减少能源消耗。但由于卫星构型等因素的影响，气动力轨道控制通常只能应用于轨道高度降低[5-7]，如果要抬高轨道高度，仍需要采用喷气主动控制。喷气主动控制是一种冲量式的变轨方式，传统方法通常将卫星和轨道的某些参数作为优化变量，构建一个开环优化问题进行设计[8-9]。对于甚低轨道卫星，由于大气阻力影响较大，卫星需要频繁进行轨道高度抬升，携带的燃料较多，导致卫星寿命期内整星质量和推力器推力变化较大。此外，目前部分卫星的轨道和姿态控制采用同一套推力器，推力器工作时卫星姿态和轨道变化相互耦合，且该耦合作用存在较大的不确定性。再考虑到甚低轨道动力学模型误差等因素的影响，采用传统的开环喷气控制很难满足现有任务提出的控制精度要求。因此，有必要基于现有的技术条件，在传统开环轨道控制算法基础上设计一种简单实用的闭环轨道控制方法，实现甚低轨道的长期稳定运行。

本文以甚低轨道卫星为研究对象，假定卫星运行于轨道高度约390 km的近圆轨道上。重点分析了大气摄动引起的轨道高度和偏心率的变化规律，设计了一种自主轨道维持方法，将传统的开环、闭环控制增益校正相结合，能显著提高轨控算法的鲁棒性，有效抑制工程实际中因卫星质量变化、推力器推力变化及姿轨控耦合作用等不确定因素对轨控效果的影响。该方法也实现了在轨自主校正轨控增益及高精度轨道的维持控制。

1 轨道摄动特性分析

卫星轨道的摄动力主要包括：地球形状摄动力；大气阻力摄动力；日、月摄动力；太阳光压摄动力；地磁摄动力；潮汐摄动力等。对于甚低轨道卫星，大气阻力摄动力相比日、月摄动力，以及光压摄动力等高1～2个数量级[10]。因此，大气阻力摄动力是决定甚低轨道寿命的主要因素。旋转大气阻尼加速度的一般表达式为

(1)

式中：CD为阻力系数；S/m为卫星面质比；ρ为卫星所在空间的大气密度；V为卫星相对大气的速度矢量，V=v-va，v和va分别为卫星和大气相对地球质心的速度矢量。在200 km以上，通常令大气旋转角速度等于地球自转角速度ne。

将式(1)分解成切向、主法向和次法向的3个分量，并略去高阶小量，得到3个大气阻力摄动加速度分量为

(2)

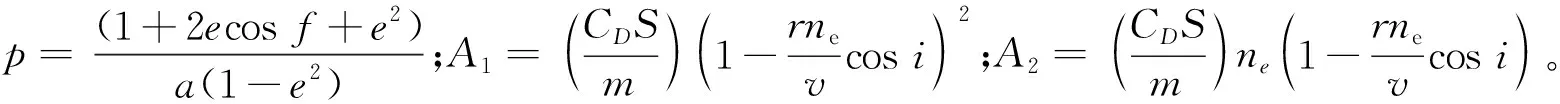
将式(2)代入高斯型摄动运动方程，仅考虑轨道高度、轨道倾角和偏心率的变化，有

(3)

由式(3)可看出，大气阻力摄动使轨道高度降低，轨道倾角及偏心率减小，即轨道逐渐变小变圆，轨道能量耗散。以本文假定的轨道高度390 km为例，取面质比S/m=0.005，大气密度ρ=1.82×10-11kg/m3，阻力系数CD=2.2，可得轨道衰减Δa=897 m/d。

考虑轨道高度由h1=390 km(对应轨道角速度n1)降低为h2=200 km(对应轨道角速度n2)，引起的轨道倾角的变化如下：

(4)

因此，对于甚低近圆轨道卫星，阻力摄动对轨道倾角、偏心率的影响非常小，主要考虑轨道高度的衰减。轨道衰减速度与大气密度呈正相关，在卫星轨道参数、面质比已知的情况下，理论上太阳活动峰年轨道衰减速度是活动平年的3～5倍。

2 自主轨道维持方法

自主轨道维持方法为在卫星轨道的远地点(平近点角M=180°处)实施轨道控制，抬高轨道高度。控制器算法包括开环轨控和轨控增益自适应调整，其中开环轨控根据先验信息建模计算每次轨控量，当轨控精度不满足要求时，可根据需要通过增益自适应调制算法计算轨控增益Kc，提高轨控精度。

2.1 自主轨道维持算法设计

自主轨道维持控制器算法包括开环轨控和闭环轨控增益调整，全部由星上自主完成。控制流程如图1、2所示。

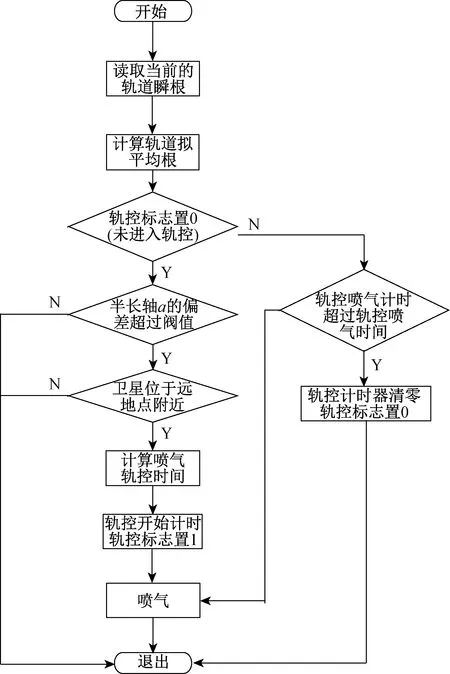
图1 星上自主开环轨控流程Fig.1 Orbit control procedure

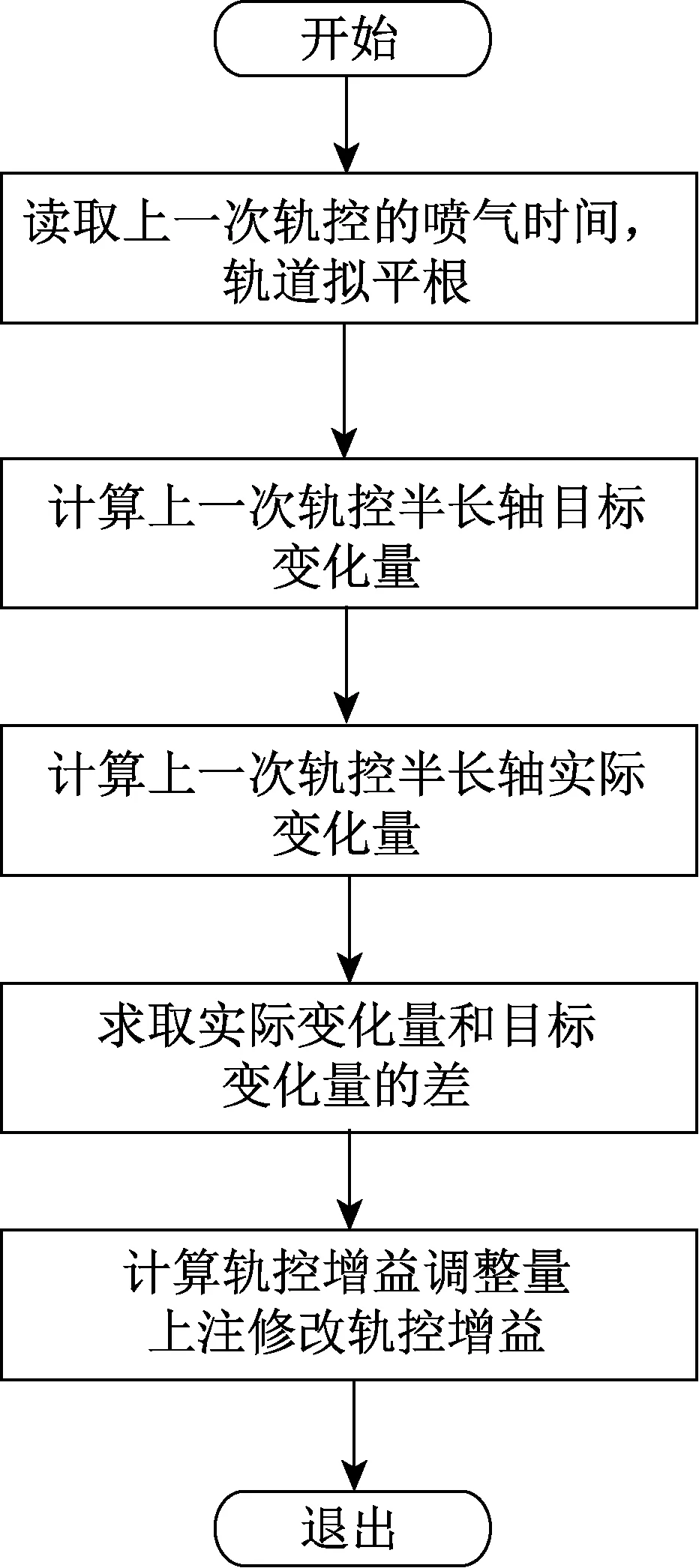
图2 增益校正流程Fig.2 Control gain correction procedure

对于圆轨道卫星，线速度和轨道半径满足

(5)

式中：a为卫星半长轴；v为卫星线速度；μ为地球引力常数。此处将椭圆轨道近似为圆轨道，所以分母中的半径r用半长轴a近似代替。卫星机械能公式为

(6)

式中：h2为卫星单位角动量的平方，h2=aμ；mt为卫星质量。

假设卫星初始轨道半长轴为a0，t时间后，由于大气阻力影响，最终轨道半长轴衰减至at，有

R=a0-at>0

(7)

衰减能量为

(8)

设每次轨控后，需要的轨道半长轴变化量为2Rc，对应轨控能量为

(9)

此外，由于每次轨控产生的速度增量很小，可将卫星轨控期间速度近似视为定值，则卫星轨控时长T满足

ΔM=FvT

(10)

因此，轨控时对应的半长轴增量与轨控时长T之间的关系为

(11)

卫星寿命期内，随着轨控次数增多，卫星携带燃料逐渐减少，卫星质量也逐渐减少，卫星燃料消耗量与卫星速度增量关系表达式为

(12)

式中：Δm为增量；w为推力器比冲(喷嘴喷出气体的速度)，对于单组元，一般有w=2 000 m/s。

每次轨控前，卫星剩余质量为

(13)

式中：m0为卫星初始质量。

通常情况下低轨卫星轨道为近圆轨道，需要将轨道偏心率控制在一定范围内。如果卫星在远地点进行轨控，则轨道偏心率会减小，在非远地点喷气，则有可能造成偏心率升高，其中对偏心率影响最恶劣的情况为在近地点进行喷气。因此，这里假设任务要求偏心率不能超过0.002 5。如果卫星初始偏心率为0，任意位置均为近地点，以最大轨控量进行变轨(10 km)，经过变轨后，卫星远地点变为Pt=a+10 000=6 771 km，近地点At=a=6 761 km，卫星偏心率变为

(14)

也就是说，最大轨控量(10 km)对应偏心率改变为0.000 7，对于有一定初始偏心率的轨道(偏心率大于0.001 5)，在远地点执行轨控，有利于偏心率的减小；如果初始轨道偏心率小于0.001 5，则远地点不再准确，可在任意真近点角进行轨控，即使在近地点执行轨控，叠加上0.000 7的轨控效果，卫星最大偏心率不大于0.002 2，可满足近圆轨道偏心率不大于0.002 5的要求。

2.2 轨控增益自校正算法设计

轨控推力器推力大小(储箱压力变化造成)和卫星质量会随卫星在轨时间的增加而逐渐变小。此外，由于轨控期间姿态依靠喷气控制来维持稳定，如果姿控推力器和轨控推力器安装在卫星同一象限，会对轨控效果产生较大影响，且该影响与轨控时间有关。上述变化主要影响喷气时长和半长轴改变量之间的比例关系，故可将这些变化近似表示成增益不确定性的形式，简化算法设计。

根据每次达到轨控目标需要进行轨控次数的多少，可通过改变控制增益或加入控制增量来计算自适应调整量，即单脉冲校正和多脉冲校正法。

1) 单脉冲校正法。该方法适用于卫星初期喷气推力较大，或半长轴调整量较小，一次轨控喷气即可实现半长轴调整的情况。实际的轨道半长轴变化量Rt和T之间应满足

(15)

式中：Kt为待求增益，设Kc为其估计值。取Rt与预计半长轴增量Rc差的平方作为性能指标，即

(16)

为提高轨控精度，可在每次轨控后，于当前比例增益Kc的基础上增加ΔKc。为使ER最小，用ER对ΔKc求偏导，并令其等于零，即

(17)

(18)

故

(19)

设第k+1次的轨控喷气时长为T(k+1)，Rc(k+1)为第k+1次轨控的目标半长轴改变量，Rt(k)为第k次轨控的实际半长轴改变量，则第k+1次轨控的控制律为

(20)

Kc(k+1)=Kc(k)+ΔKc(k)

(21)

(22)

若轨道参数、质量和喷气推力中存在随时间变化的量，为了防止增益估计值出现大幅振荡，增益改变量需要乘以一个系数来改变增益趋近速度，有

(23)

2) 多脉冲校正法。该方法适用于卫星任务后期喷气推力不足，半长轴偏离较大，需要多次轨控实现半长轴调整的情况。

设Rc(k)为第k次轨控的目标半长轴改变量，Tmax为单次轨控时间长度上限，Rt(k)为第k次轨控的实际半长轴改变量，T(k)为第k次的轨控时间，Kc(k)为第k次轨控的修正量，则而第k次轨控时间满足

(24)

第k次轨控多喷的喷气时间修正值为

(25)

令

(26)

则第k+1次喷气时间可通过式(27)、(28)计算：

(27)

(28)

此处ΔKc(k)可乘以一个系数来调整收敛速度，有

(29)

式中：0<α<1。

通常情况下Rc(k)直接取目标轨道半长轴和当前轨道半长轴的差。如果Kc(k)与真实值的偏差较大，即Rc(k)较小，则单次轨控实际产生的Rt(k)较大，可能因ΔKc(k)过大导致Kc(k+1)<0，进而导致输出的轨控时间T(k+1)<0，产生无意义结果。为防止这种现象出现，此处对Kc(k+1)进行如下处理：

(30)

式中：0<β<1。设计完成自主轨控策略后，需要根据任务要求分析轨道控制的频次及每次轨控持续时间的范围，为其他分系统设计提供合理的输入条件。

2.3 轨道维持频次分析

首先对相邻2次轨控的间隔时间，即卫星自主轨控的频次进行分析。太阳活动峰年卫星轨道高度下降速度为897 m/d，太阳活动平年轨道下降速度为179 m/d。

工况1卫星质量为4 000 kg，采用4推力器进行轨控，每台推力器推力为12 N，每次轨控从Δa=-5 km控制到Δa=5 km，即每次抬高轨道10 km，则卫星平年2次轨控的时间间隔为10 000/179≈55.9 d，该值可视为理论上卫星2次轨控间隔时间的最大值。

工况2卫星寿命末期，质量为3 000 kg，采用2台推力器进行轨控，每台推力器推力为2 N，每次轨控只能从Δa=-1 km控制到Δa=1 km，即每次抬高轨道2 km，则卫星峰年2次轨控的时间间隔为2 000/897≈2.2 d，该值可视为理论上卫星2次轨控间隔时间的最小值。故卫星相邻2次轨控的间隔时间为2.2～55.9 d。

2.4 轨道维持控制时长分析

考虑卫星每次轨控的喷气时间，根据工程实际要求，分3种进行讨论。

1) 设任务初期轨控推力为48 N，高度改变量为10 km，任务末期轨控推力为4 N，轨道高度改变量为2 km。该情况的2个边界状态与轨控频次分析中的2个工况一致。单次轨控喷气时间为

(31)

经过任务描述可发现，任务选择的轨道高度改变量与卫星质量和推力器输出有关。如果Rc连续变化，则在一定范围内，Rc、mt和F间可假设存在一定的线性关系，有

Rc=k1mt+k2F

(32)

通过工况1和工况2的设定，计算得到k1=0.2,k2=87.3。同样，mt和F之间也存在一定线性关系，代入2种工况可得

mt=17F+3 030

(33)

则单次轨控喷气时间变为

[0.2(17F+3 030)+87.3F]=

(34)

令∂T/∂F=0，可得F=34.5 N，取a=6 761 km，对应线速度为v=7 672 m/s，对应的喷气时间约为450 s，取两个边界值F=48 N和F=4 N，可得喷气时间约为456 s和861 s，所以F=34.5 N对应的是喷气时长最小值，卫星轨道高度保持控制的最大喷气时长为861 s，最小喷气时长为450 s。F和T之间的关系如图3所示。

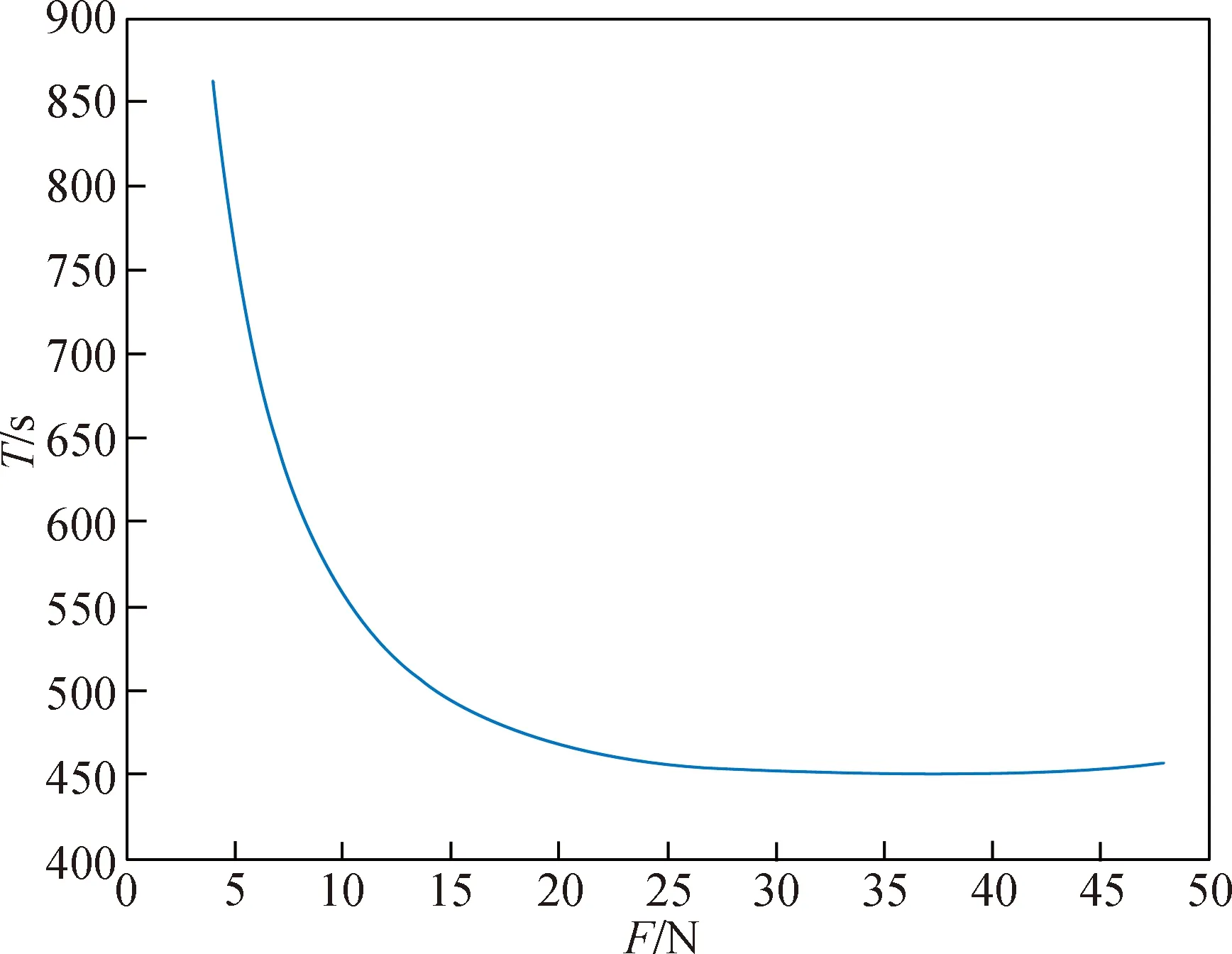
图3 F和T之间的关系(情况1)Fig.3 Relationship between F and T for case 1

2) 设任务初期轨控推力为48 N，末期轨控推力为4 N，轨道高度改变量均为10 km。该情况下推力F和卫星质量mt之间仍满足式(33)所示的关系。将喷气时长T的计算式(31)代入式(33)，消去mt可得

(35)

F和T之间的关系如图4所示。

图4 F和T之间的关系(情况2)Fig.4 Relationship between F and T for case 2

喷气时长最大值约为4 446 s，最小值约为460 s。

3) 设任务初期轨控推力为48 N，末期轨控推力为4 N，轨道高度改变量均为2 km

该情况下F和T之间满足式(38)，其关系如图5所示。

图5 F和T之间的关系(情况3)Fig.5 Relationship between F and T for case 3

喷气时长最大值约为889 s，最小值约为92 s。

3 仿真结果

主要仿真参数如下。

1) 卫星轨道高度：390 km。

2) 卫星轨道初始偏心率：0.001 2。

3) 卫星质量：4 000 kg(单脉冲校正仿真)，3 000 kg(多脉冲校正仿真)。

4) 最大轨控推力大小：24 N(单脉冲校正仿真)，4 N(多脉冲校正仿真)。

5) 最大姿控推力大小：6 N(单脉冲校正仿真)，2 N(多脉冲校正仿真)。

6) 半长轴调整阈值：2 000 m。

7) 单次轨控时间上限：600 s。

8) 推力偏差：20%。

9) 质量偏差：20%。

10) 远地点计算偏差：10°。

为了突出本文所设计算法的优势，首先对目前星上普遍采用的传统的无轨控增益校正算法进行了仿真，如图6所示。单脉冲增益校正方法的仿真结果如图7所示，为了减少仿真时间，增加轨控频次，模型中加大了大气干扰力的量级，即加快了轨道高度降低的速度。在采用无轨控增益校正算法时，轨控误差较大，误差趋于稳定后接近500 m。采用轨控增益校正算法后，第一次轨控从-4 km的半长轴偏差开始，结束后轨控误差非常大，超过2 km，控制增益修正律迅速修正了轨道控制参数，使后面的轨控误差迅速减小(<30 m)。此外，当偏心率较大时，每次轨控会导致偏心率变小，偏心率一直维持在一个较小的范围内(<0.000 3)，说明轨道高度维持控制不会改变轨道的近圆特性。

图6 无轨控增益校正的仿真结果Fig.6 Simulation results without control gain self-scheduling

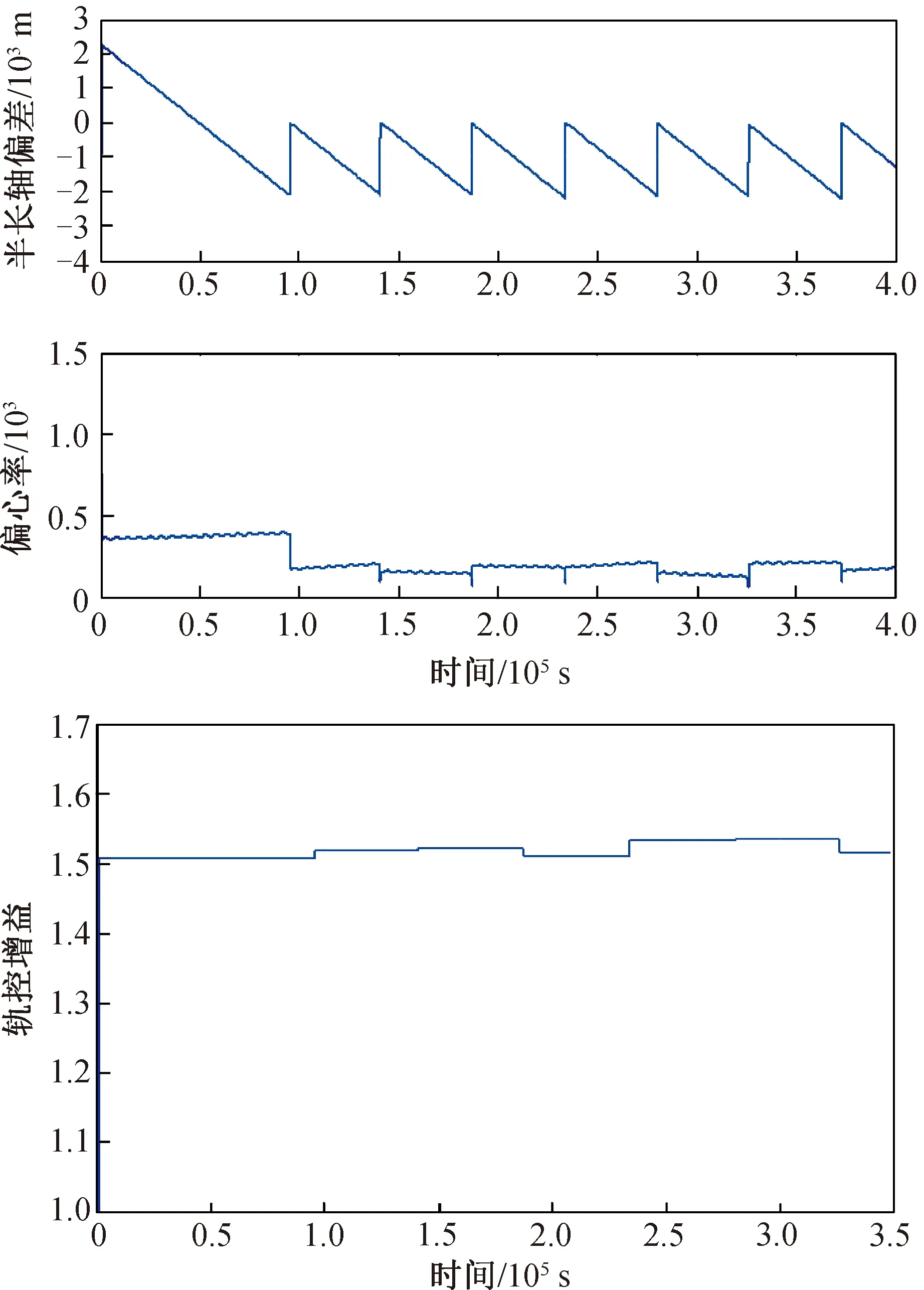
图7 单脉冲增益校正的仿真结果Fig.7 Simulation results with control gain self-scheduling for single pulse mode

多脉冲增益校正方法的仿真结果如图8所示，可以看出轨控增益在前两次轨控后被迅速修正，之后的几次轨道控制都实现了较高的精度(<30 m)。

图8 多脉冲增益校正的仿真结果Fig.8 Simulation results with control gain self-scheduling for multi-pulse mode

4 结论

本文分析了甚低轨道卫星的摄动特性，设计了自主轨道维持策略及轨控增益校正算法，可在卫星质量偏差、推力器推力偏差等不确定的情况下依然保持较高的轨道维持控制精度。仿真表明：在同时考虑较大卫星质量和推力器偏差，较大初始轨道偏心率和轨控位置偏差的情况下，均能较好地完成自主轨道维持任务，轨控精度优于30 m，偏心率优于0.000 3。本文所提出的算法具有较强的工程应用价值，计算过程简单，运算量小，可由目前的星载计算机在轨实现，满足未来甚低轨道卫星长期稳定运行需求。