基于IHS变换的Gram-Schmidt改进融合算法研究
刘 川,齐修东,臧文乾,黄祥志,杨秀峰
(1.河南理工大学 测绘与国土信息工程学院,河南 焦作 454000; 2.中国科学院 遥感与数字地球研究所,北京 100101; 3.北华航天工业学院,河北 廊坊 065000)
GF-2卫星是我国自主研制的首颗空间分辨率优于1 m的民用光学遥感卫星,搭载有两台高分辨率1 m全色、4 m多光谱相机(PMS1/PMS2),是目前我国分辨率最高的光学对地观测卫星[1]。自GF-2卫星发射至今,地面站已获取到大量高分辨率的遥感数据。如何将GF-2卫星全色与多光谱影像进行融合处理,得到高分辨率的多光谱影像仍是目前的关键技术之一。
随着遥感技术的发展,定量地解译和反演目标参数已成为迫切的需求,这就要求融合算法不仅能增加影像的空间纹理信息,还要保持光谱的原始信息,即不发生或尽可能少的发生信息失真[2]。针对这一需求,学者们进行深入研究,并取得一定的成果。如张涛等[3]提出一种结合Gram-Schmidt变换的高光谱影像谐波分析融合算法,该算法有效地提高了高光谱影像的空间分辨率;Sun W等[4]提出一种新的NNDiffuse融合算法,该算法针对国产高分辨率影像融合有着较好的效果;李慧娜[5]对像素级遥感影像融合算法进行对比分析研究并且提出了一种基于局部方差加权的改进型IHS融合算法,该算法设置最优窗口对影像进行窗口方差归一化处理,结果表明该算法能够在有效的提高融合结果清晰度的同时保持图像的光谱信息;张静等[6]利用IHS变换与改进的多进制小波变换相结合对多源遥感图像进行数据融合,使融合后的数据既减少了IHS变换引起的图像光谱失真现象,又具有高空间分辨率的优点;侯翔文[7]引入加权平均算子和高通滤波算子,对IHS变换融合方法进行改进,改进算法在清晰度和光谱扭曲度这两个“互斥”的指标上得到双重提高,实现提高融合质量的目的。
GS变换算法可以较好地改善原始影像的空间细节特征,且能在较大程度上保持原始影像的光谱物理特性[8]。然而,此算法在针对GF-2卫星多光谱和全色影像进行融合处理时,仍会存在较为明显的光谱失真和细节模糊现象。鉴于此,本文将IHS变换引入GS算法中,提出一种基于GS变换和IHS变换的改进融合算法。
1 算法介绍
1.1 GS变换
GS变换融合算法就是利用正交变换的数学方法对影像矩阵进行计算,实现消除影像信息冗余以及各波段之间的相关性的目的[9]。该算法首先对多光谱波段按照一定的权重进行计算,模拟出低分辨率的全色影像作为GS1;然后用模拟的GS1进行GS正变换,计算GS1波段和全色波段的均值及标准差,对全色波段和GS1波段进行直方图匹配;最后用匹配后的全色波段替换GS1进行GS逆变换,得到高分辨率多光谱影像。
1.2 IHS变换算法
IHS(亮度、色调、饱和度)彩色模型是基于彩色描述的图像处理算法的理想工具,该模型可在彩色图像中携带的彩色信息(色调和饱和度)中有效的消去强度分量的影响[10]。IHS变换融合算法是基于IHS彩色模型提出的一种影像融合算法,该算法首先将RGB分量变换至IHS空间;然后分别计算I分量和全色影像的均值及标准差,对全色影像和I分量进行匹配;最后用全色影像替换I分量进行IHS逆变换。
1.3 IGS算法
GS变换融合算法可以在提高影像空间分辨率的同时,有效保留原始影像的光谱信息,而GS变换的模拟第一分量对影像融合效果影响较大,本文在此基础上提出IGS算法,算法流程如下:
1)原始多光谱影像与全色影像进行几何精配准,并将多光谱影像重采样至全色波段同样大小;
2)将多光谱影像进行IHS变换,得到亮度分量I;
(1)
3)用I分量作为模拟GS变换第一分量,进行GS正变换,第T个GS变换分量由前面T-1个GS分量构造,即
(2)
式中:GST为当前GS正变换的第T波段;BT为参与变换的原始多光谱波段,波段均值为
(3)
式中:C和R分别为影像的列数和行数,参数Φ(BT,GSi)为
(4)
式中σ(BT,GSi)为波段B和波段GS的协方差,波段标准差σ为
(5)
4)首先分别计算I分量和全色波段的均值及标准差,将I分量与全色波段进行直方图匹配,则
(6)
式中:pan为全色波段;I′为直方图匹配后的I分量。然后设置3*3的滑动窗口,对I′分量和全色影像分别计算窗口内象元的标准差,按式(7)进行判定,即
(7)
其中,Mpan(i,j)为修正后的全色影像;Pan(i,
j)和I′(i,j)分别为全色影像及分量滑动窗口中心象元值;Stdpan和StdI′为全色影像及分量的滑动窗口内的标准差;
5)用修正后的全色波段替换GS变换第一分量,然后进行GS逆变换得到分辨率多光谱影像,即
BT(i,j)=(GST(i,j)+μT)+
(8)
IGS算法的完整流程如图1所示。

图1 IGS算法流程
2 实验结果分析
2.1 实验结果
实验数据选择3景标准景GF-2卫星遥感影像,影像涵盖植被、水体、建筑、裸地、山体等各种典型具有代表性的地物地貌。
为了对比验证IGS算法的效果,选择IHS变换、GS变换、PCA变换3种常用的算法对所选数据进行融合,所有结果在ENVI中选择真彩色波段组合进行1%的线性拉伸,然后截取部分融合结果,分为植被和建筑两个区域进行对比,如图2和图3所示。

图2 建筑区域融合结果

图3 植被区域融合结果
2.2 质量评价
融合效果评价是影像融合处理不可或缺的一个环节,通过对融合算法的效果和性能进行分析、测试和评估,可以进一步调节算法参数,使整个融合处理过程得到优化[11]。本次试验综合考虑融合后影像的清晰度、光谱特性以及信息量3个方面的因素,首先采用目视判别的方式对全部融合结果进行对比分析,然后选择基于单一图像统计量的信息熵、平均梯度和基于原始图像统计量的相关系数、偏差指数和扭曲程度这5种指标对结果进行定量分析。
2.2.1 定性评价
首先将本次试验结果与原始多光谱和全色影像作对比,从目视效果上看,4种算法处理后的影像在空间细节的辨识度方面均有明显的提高,而且都能在一定程度上保留原始影像的光谱信息。
然后对比图2和图3中的4种融合结果,可以看出4种结果的纹理细节都能得到增强,不同地物可以清晰的辨认出来,尤其是建筑区域融合效果更加突出。在光谱方面,IHS变换算法在水体、建筑以及裸地部分的色彩发生轻微的变化,而在植被区域光谱失真比较严重,图3(c)中可看到绿色部分明显偏蓝;PCA变换算法以及GS变换算法在建筑、水体、裸地区域的光谱色彩比较接近原始多光谱影像,但是在植被区域都存在有光谱失真的现象,尤其是植被边缘部分,失真现象比较突出;IGS算法融合结果在光谱保留程度方面,要明显优于其它3种算法,在图3中的植被区域,图3(d)的色彩效果最接近原始多光谱影像。
2.2.2 定量评价
为进一步验证IGS算法的效果,选择信息熵、平均梯度、相关系数、偏差指数和扭曲程度5种评价指标对融合结果进行定量评价,5种指标的统计值特性[12]如表1所示。

表1 评价指标特性
通过用C++语言调用GDAL库函数的方法,编程计算4个算法融合结果的各个定量评价指标,计算结果如表2所示。
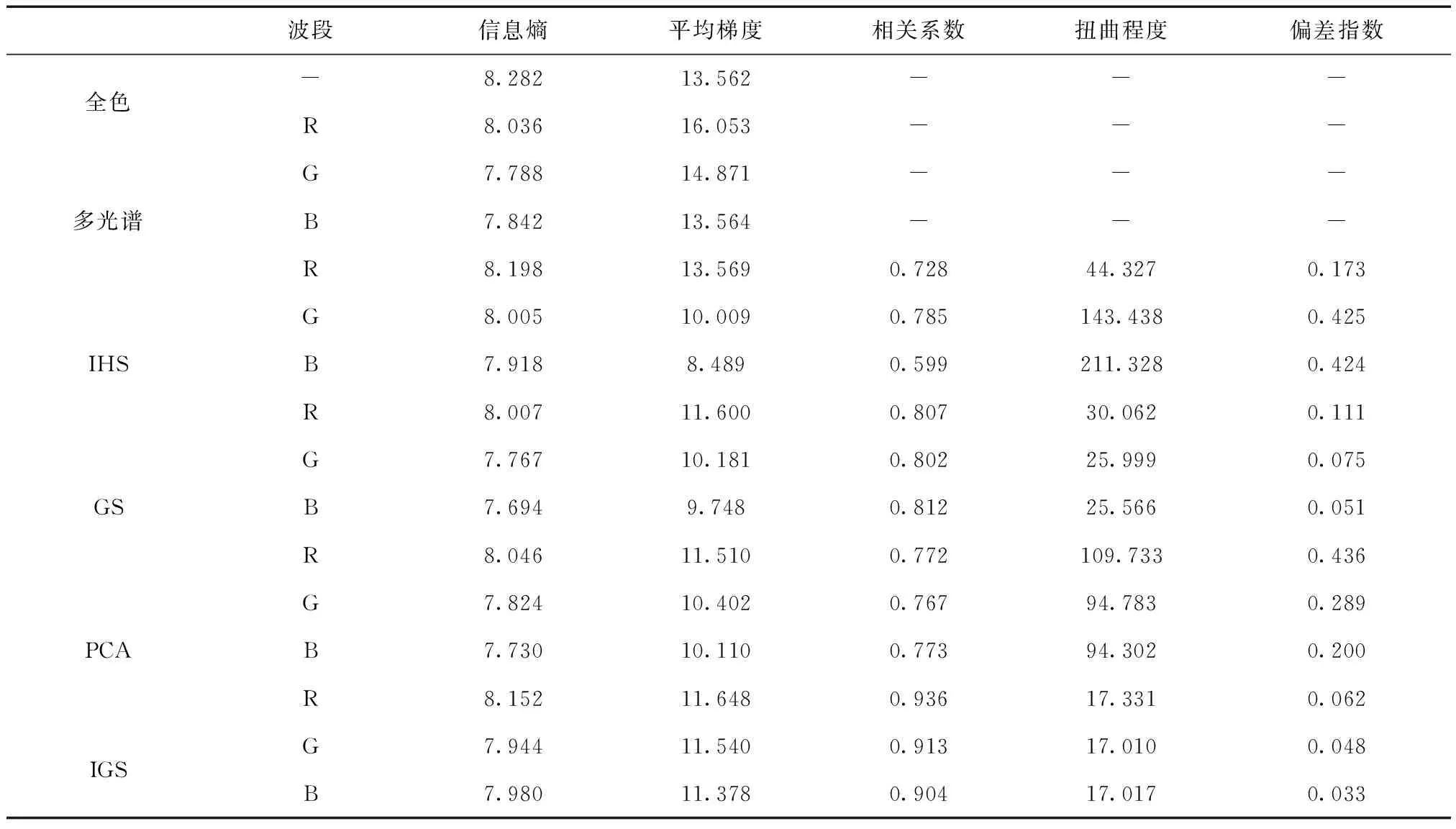
表2 质量评价结果
从表1中可以看出信息熵反映了影像包含的地物信息量;平均梯度表达了影像的空间纹理细节特征;相关系数、偏差指数和扭曲程度在表达光谱信息特性方面一致,均反映了地物与原始影像的差异。为使评价信息更加直观,取信息熵、平均梯度和相关系数3个指标绘制折线图如图4所示:
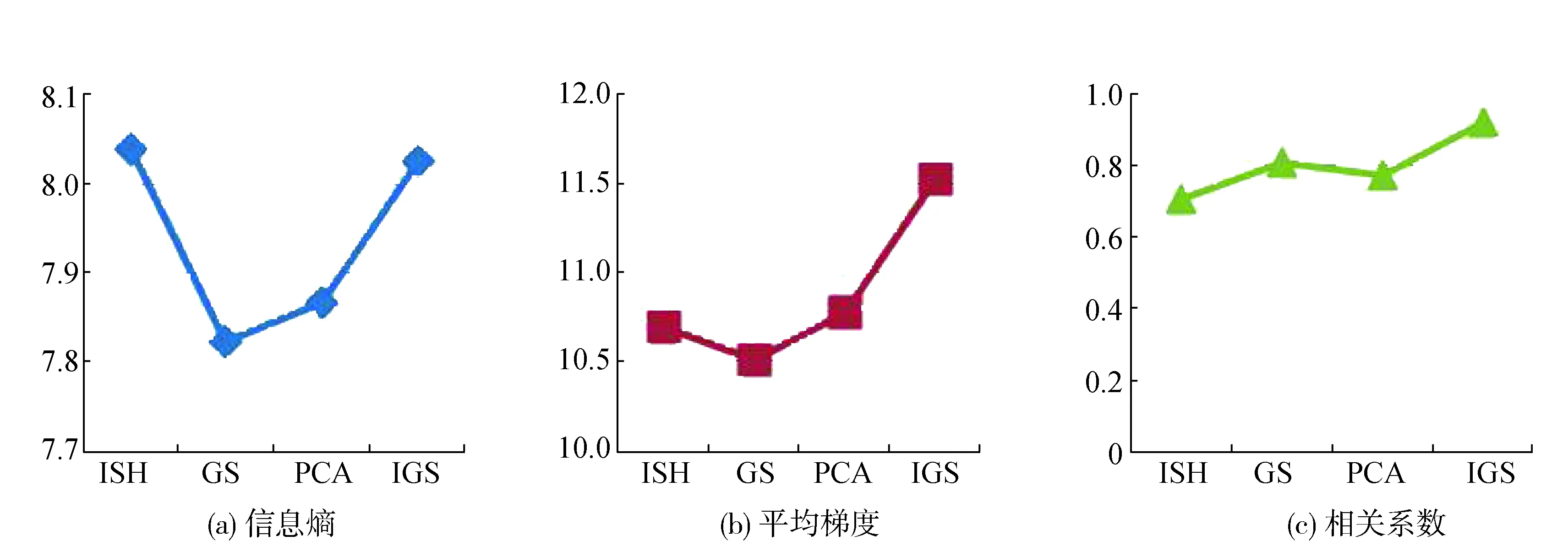
图4 质量评价折线图
从表2和图4中可以看出,IGS算法的信息熵指标接近于IHS变换算法,平均梯度在R波段小于IHS变换算法,但是要高于GS变换算法和PCA变换算法,而且IGS算法3个波段的平局梯度较为接近,说明IGS算法在空间纹理细节提高方面较大程度上继承了IHS变换算法的优点;IGS算法的相关系数指标明显高于其它3种算法,扭曲程度和偏差指数指标最小,即该算法的融合结果在光谱信息上最接近原始多光谱影像,证实了IGS算法在原有GS变换光谱信息保留较好的基础上还有所提高。
综上,可以确定本文IGS算法兼具IHS变换和GS变换两种算法的优点,能够在保留原始多光谱影像的光谱信息的基础上,明显提高影像的空间分辨率,在对GF-2卫星影像融合处理上优于其它3种算法。
3 结束语
本文基于IHS变换融合算法和GS变换算法,提出一种改进融合算法,先对原始多光谱影像进行IHS变换,取变换后的I分量作为GS变换第一分量,进行GS正变换,为了在提高影像空间细节的同时保留光谱信息,选择用滑动窗口对I分量和全色波段进行滑动处理,并用标准差作为判定条件决定窗口中心象元取值,构造出新的全色影像替换GS变换第一分量进行GS逆变换,得到融合结果。为了验证算法的有效性,选择GF-2卫星数据进行融合处理,并对比IHS变换、GS变换和PCA变换算法的融合结果,选择主观和客观两种方法进行质量评价,结果表明,IGS算法优于其它3种算法,兼具IHS变换和GS变换两种算法的优点,既能较大程度提高影像清晰度,又能保留影像的光谱信息。

