开孔补强对受剪复合材料工字型梁腹板稳定性的影响研究

张 健，刘 伟，高维成

（哈尔滨工业大学 航天科学与力学系，哈尔滨150001）

0 引 言

由于可减轻结构重量和改进结构设计，复合材料薄壁梁越来越被广泛应用于船舶、车辆、航空航天等工业领域。然而实际工程结构由于功能需求或是涉及制造工艺等问题，难以避免地需在复合材料承力结构上进行开口设计，这必然导致改变其力学响应，比如开口边缘应力集中或结构屈曲承载能力下降，影响产品使用寿命和安全。另外薄壁结构在压缩或剪切等作用下常易发生的失效模式为屈曲破坏。因此，对复合材料结构开口问题的研究显得尤为迫切，特别是在面内载荷下开口对结构稳定性的影响更应受到重视和进行量化研究。

近四十多年来，含开口复合材料结构的稳定性问题已经在国内外有了大量的研究[1-5]。Nemeth[6]对在1972年到1993年之间关于含开口复合材料板的屈曲和后屈曲行为的研究成果进行了综述性评述，主要考虑到开口大小、形状、铺层顺序与角度、加载方式和边界条件等影响稳定性的因素。Bailey和Wood[7]进一步研究了含圆形和方形开口复合材料方形层合板的后屈曲行为。Kumar和Singh[8-10]系统研究了含开口层合板在面内压缩与剪切载荷共同作用下铺层方式、开口形状以及载荷方向对其屈曲和后屈曲行为的影响。Guo等[11-12]探讨了在剪切载荷作用下的开圆孔复合材料层合板结构应力集中现象，并对开口进行补强设计试验研究。姚辽军等[13]基于经典层合板理论，将复合材料板等效为正交各向异性板，研究了不同孔径大小、铺层比例等影响参数下的应变集中系数变化规律。

目前关于含开口复合材料结构的各种仿真模型的建立及其力学分析方法和实验研究等方面都取得了很大的进展，但现有的基于实验研究的仿真模型都有自己的适用范围和局限性。另考虑到复合材料本身特殊性、结构缺陷敏感性、复杂边界效应等诸多因素会影响结果的精确性，因此对含开口结构进行试验分析和验证仍然是很有必要和迫切需求的。本文以含开口复合材料工字型梁腹板为研究对象，通过开展试验和仿真计算研究其在剪切载荷作用下的力学响应，并分析开口与补强对复合材料工字型梁腹板稳定性的影响，可为指导含孔梁腹板结构优化设计及其在船舶等实际工程上的选型应用提供试前分析依据和参考思路，具有工程指导意义。

1 试验设计

1.1 试验件构型

图1 复合材料工字型梁腹板试验件（含补强）Fig.1 Test specimen of composite I-section beam(with reinforced)

本文所研究的含长圆形开口复合材料工字型梁腹板是飞机及船舶工程中的典型受力构件，试验件外形几何尺寸取为360 mm×180 mm×2.28 mm，分为补强和未补强开口两种工况（简记为R型件与C型件），每种工况6件，如图1（a）所示；工字型梁腹板正中心设置长轴2a＝121 mm、短轴2b＝66 mm的长圆形开口，对补强试件的开口区域采用单面插层补强方式，其具体尺寸参数如图1（b）所示。根据所受载荷形式和试验件尺寸，设计了如图2所示的试验加载装置，将复合材料工字型梁一端固定在试验架上，在另一自由端施加竖向剪切载荷来进行试验。试验件由中强度高模量树脂基碳纤维增强复合材料T800/X850对称铺设构成，铺层顺序见表1，T800/X850材料常数见表2。

表1 试验件铺层顺序Tab.1 Stacking sequence of test species

表2 T800/X850材料常数Tab.2 Material properties of T800/X850

图2 工字梁试验模型图Fig.2 The experiment model of I-section beam

1.2 试前准备

为了研究开口与补强对复合材料工字型梁腹板稳定性和破坏模式的影响，根据试前有限元仿真分析的结果对应变测量点进行了优化排列，试件的正反面成对应方式布置应变测点，共18个，分别测量与试验件翼缘成45°、-45°、0°、90°方向的应变，所有试件应变片布置和编号均相同，如图3所示。

图3 试验件应变片位置和编号（背对背粘贴）Fig.3 Strain film layout

试验件在设计加工时在边缘处已预留宽度40 mm的夹持区，便于卡具夹持试件。同时为保护试件在夹持边框或是连接处不被螺栓孔边挤压发生破坏，夹持边框正反两面分别粘贴170 mm×40 mm×2 mm的铝合金条。

本文所有试验均在微机控制电液伺服加载系统DGS-5上进行，加载方式采用多级加载直至试验件破坏，试验整体装配及调试后加载照片如图4所示。

图4 试验件装卡后状态Fig.4 State of test beam after assembly

2 结果与讨论

2.1 试验结果分析

由于试验件数量和工况偏多，试验所测得数据量比较庞杂，限于篇幅，现以未补强开口试件C3为例，选取长圆形开口周边上与试验件纵向成45°、-45°、0°和90°方向的应变水平较高的12个重要测点以及非开口区域2个相对测点，来研究开口工字型梁腹板的长圆开口边上应力/应变集中及稳定性问题。

图5给出了工字型梁腹板C3试件开口周边关键测点的载荷—应变关系曲线，以分析其稳定性问题及其破坏过程。分析如下：（1）由图5（a）可知，从初始加载直至其发生屈曲之前，沿45°方向上的正反面两对测点（测点15与65、测点36与86）的应变值及变化趋势完全相同，绝对值随载荷增加呈线性增长，应变一致性关系非常吻合，表明测点正反面对应性和面内对称性保持非常好，亦可以说明设计的试验方案及夹具合理可靠；（2）由于试件本身的对称性，在结构未发生横向弯曲变形前正反面对应测点的应变是一致的，在加载载荷未达到12.38 kN之前，图5中的对应测点的应变均符合这一规律；载荷超过12.38 kN时，如图5（c）所示，测点64由拉伸逐渐转变为压缩，而测点14应变随载荷增加而加速变化，结构出现横向弯曲变形。观察图5（b）、（d）﹑（e）中的测点，在载荷增加到12.38 kN时，曲线斜率均发生明显变化，说明试件此时发生屈曲，即可判断Nxycr=12.38 kN为试验件的临界屈曲载荷；（3）在试件发生屈曲后继续加载，此时进入了后屈曲承载阶段，当试验载荷为17.42 kN时，试验件发出轻微的层间分离声音，结构开始发生局部损伤；继续加载可目视到试验件发生明显的屈曲变形；直到试验载荷为25.6 kN时，试件破坏并在破坏的瞬间发出较大的声响，试件完全失去承载能力，加载结束。由此可知其极限破坏载荷是结构临界屈曲载荷的2倍左右，可见本文基于前后梁结构所设计的含开口复合材料工字型梁腹板能有效地利用其后屈曲承载能力。（4）对比图5（a）与5（c）可知，沿45°方向上的测点应变（4 000 με）是远远小于沿-45°方向上的正反面两对测点（-13 500 με）；在加载到17.42 kN时，沿-45°方向上的测点37出现应变突跳并且破坏，而且梁腹板开口边缘多处发生了局部破坏，如劈丝、分层等破坏形式（如图11所示），说明受拉纤维失效不是引起梁腹板失稳破坏的主要原因，而在非对角拉伸方向受压，发生屈曲破坏是试件的主要破坏模式。

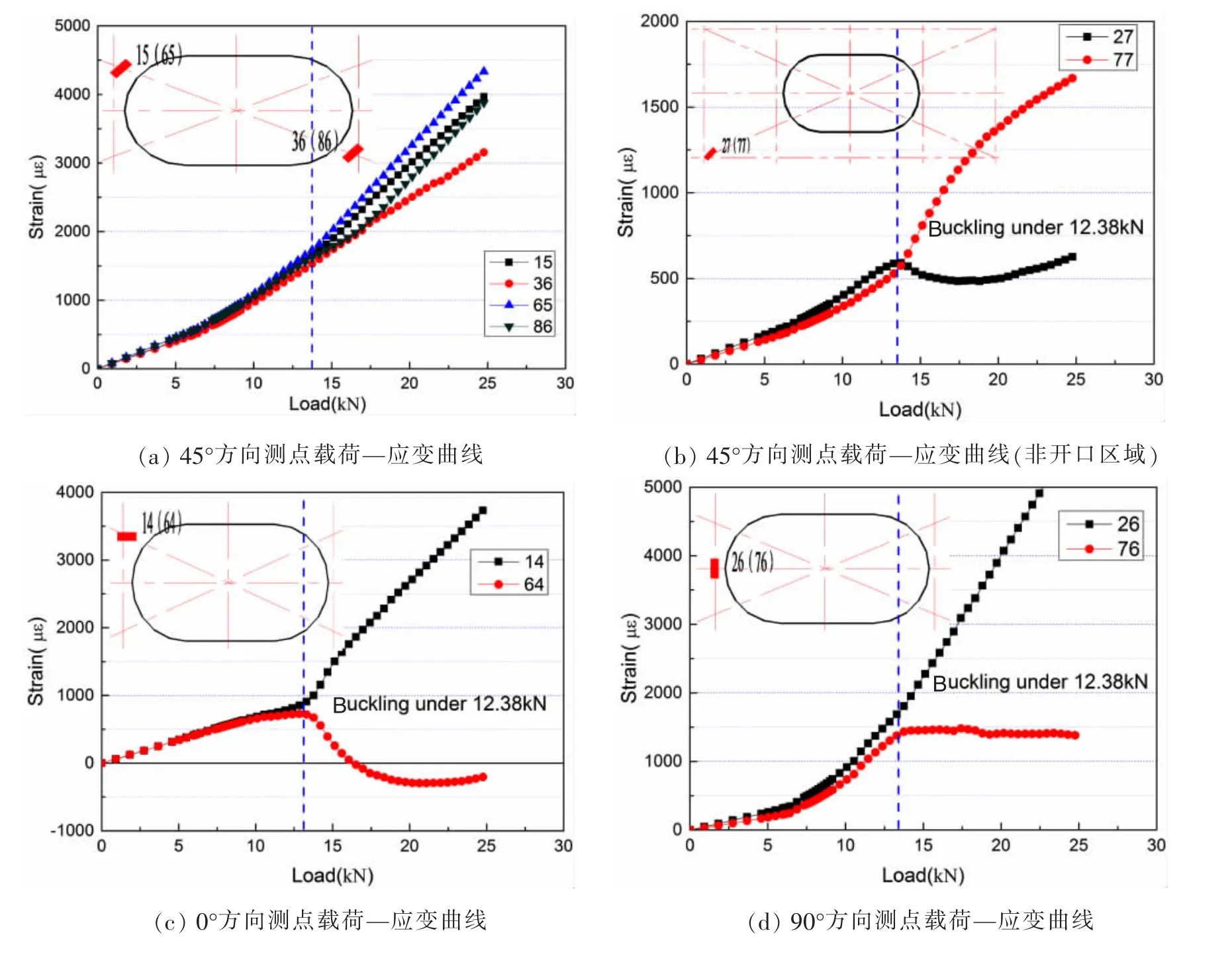
图5 C3试验件最大应变测点载荷—应变Fig.5 Strain-load curves of gauges on the test I-section beam

由于单层的各向异性，复合材料层合板结构承受载荷作用时在不同方向的铺层所体现出的应力集中现象也各不相同。为了研究结构宏观应力/应变场，根据试验件受力情况及前期分析结果，选取长圆形开口边上部分的正反面及面内对应应变测点来研究开口薄壁梁的口边应力集中现象。表3、4分别为开口和带补强的试验件的关键点应变测量值。由表3和表4均可知，±45°方向应变在试验所测得的各方向中最大，这与在面内剪切载荷作用下层合结构±45°方向铺层是其主要承载层相符。对比表3中的45°方向上开口与非开口区域测点15和77，在临界屈曲载荷12.38 kN作用下开口梁腹板最大应变是未开口区域的3倍，且在0°﹑90°方向上的应变也有明显的变化，可见梁腹板开口附近具有显著的应力/应变集中现象。比对表3和表4中相应测点的应变，分别在相同载荷12.85 kN、17.42 kN作用下，含开口补强的试验件在开口与非开口区域的应变都远远低于未补强的，这表明对开口区域进行插层补强设计能有效地降低应力/应变集中程度。表4为开口补强试验件的关键点应变测量值，其中编号超过50的测点位于单面补强面上，对比分析可以发现45°方向上开口与非开口区域测点15和77，其应变相差将近3倍，也可说明开口补强设计是很有效和必要的。

表3 长圆开口试验件的关键点应变测量值Tab.3 Experimentally measured strain values of gauges at the elliptical cutout edge(×10-6)

表4 开口补强试验件的关键点应变测量值Tab.4 Experimentally measured strain values of gauges at the reinforced elliptical cutout(×10-6)

2.2 试验结果与仿真结果比对分析

基于有限元软件MSC.Patran/Nastran平台，分别对带长圆形开口和带开口补强的复合材料工字型梁腹板建立了有限元模型，采用带弯曲和薄膜刚度耦合任选项的四边形等参单元QUAD4，进行了剪切载荷下的有限元仿真分析。建模时采用共用节点法，使翼缘与腹板通过共用节点连接，从而整体建模；对长圆形补强区域采用偏置方法，选用QUAD4单元是因为翼缘与腹板是共固化一次成型且其分析计算结果精度比采用梁板单元模拟要高。因为工字型梁腹板试验件是一端与试验架固定，在另一自由端施加竖向剪切载荷，所以有限元模型边界条件可以将固定端模拟为固支边界条件，而加载端简化为简支边界条件，并限制翼缘的面外位移，如图4所示。

在加载端施加竖向的10kN剪切载荷，利用SOL105求解器进行线性特征值屈曲计算，可得到含开口未补强的工字型梁腹板试件的一阶屈曲模态图，见图6，得其第一阶屈曲因子为1.249 5，即屈曲失稳临界载荷为12.495 kN。同理，可得补强试件的屈曲载荷为25.794 kN，两种类型试件发生的屈曲模式与位置是一致的，如图7所示。图8为利用SOL106求解器进行非线性静力分析得到的含长圆形开口工字型梁腹板在30 kN剪切载荷作用下的非线性变形，所施加的剪切载荷直到结构出现首层破坏。

表5为试验值与仿真计算结果的比对。由表5可知，含长圆形开口工字梁腹板的屈曲载荷仿真计算值为12.495 kN，与试验平均值12.76 kN吻合非常好，误差仅在2.1%左右，而带有补强的屈曲载荷仿真值与试验结果误差也小于5%。对比未补强的屈曲载荷，插层补强使试验件稳定性提高88%，极限破坏载荷也提高了46.3%。两种类型试件的破坏载荷分别是其屈曲载荷的2.11倍、1.59倍，说明本文所设计的复合材料工字型梁腹板充分发挥了该种结构的效能。

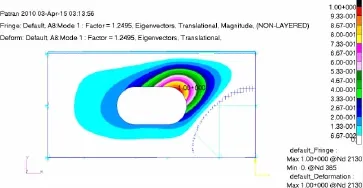
图6 带开口工字型梁在10 kN作用下的一阶屈曲模态Fig.6 The first buckling mode of I-section beam with an elliptical cutout under a load of 10 kN

图7 带开口补强工字型梁在10 kN作用下的一阶屈曲模态Fig.7 The first buckling mode of I-section beam with a cutout reinforced under a load of 10 kN

图8 带开口补强工字型梁在30 kN作用下的非线性变形Fig.8 Nonlinear deflection of the I-section beam under shear load 30 kN

表5 试验值与计算值比对（单位：kN）Tab.5 Comparison between test and numeration results(Unit:kN)

复合材料结构的破坏模式比较复杂，常见的有纤维断裂、基体开裂、纤维基体剪切分离、层间剪切破坏等形式，但是这些损伤首先在层合板局部产生进而扩展到整个结构导致整体破坏。因此，本文选用“蔡吴失效准则”[14]预测工字型梁的首层破坏载荷，以此了解含开口工字梁腹板的破坏模式，具体形式如下：

别代表了单层板在纵向和横向的抗拉和抗压强度；F6为抗剪强度和G=-0.5。

图9为在剪切载荷下工字型梁腹板的载荷—位移曲线，从图可知，含开口和补强的工字型梁的首层破坏载荷分别为18.25 kN和32.3 kN。本文在非线性静力仿真分析中得到模型在竖向剪切载荷30 kN作用下的应力分布，并采用蔡吴失效准则对其进行失效判定。经失效分析，给出图10中失效指数的分布，可以看出最先达到失效指数的区域为A，以预测试验件最终破坏应该发生在对应的区域。

图11为试验件发生损伤最严重区域的破坏形貌。与图10比对可知，仿真中利用蔡吴失效准则预估损伤的区域与试验中可目测破坏的区域吻合得非常好。

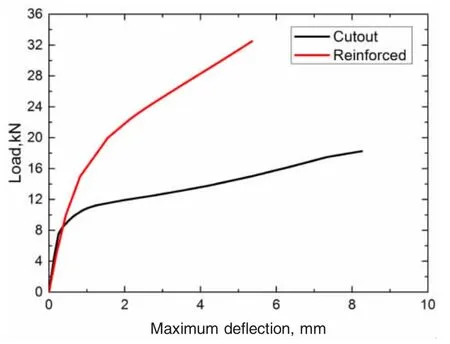
图9 在剪切载荷下工字型梁腹板的面外最大位移—载荷曲线Fig.9 Load-deflection responses of the I-section beams with a cutout

图10 在剪切载荷30 kN下蔡吴失效判定指数分布Fig.10 Tsai-Wu failure indices under shear load 30 kN

图11 试验件破坏区域形貌Fig.11 Failure situation of the test panel

图12为加载到破坏的全程载荷—位移曲线。分析该曲线并结合载荷—应变曲线以及试验过程中的观察记录，可知其初始破坏载荷分别为17.52 kN，30.9 kN，与仿真结果（18.25 kN和32.3 kN）的误差均在5%以内，误差原因在于试验件在制造或装配过程中都有细微的缺陷，而非完善的。破坏过程可描述如下：试验件从初始加载到12.38 kN左右时首先发生屈曲，但是未立即发生破坏；随着载荷的增加，孔边出现明显的变形，向一个方向凸出，此时可断断续续听到轻微响声；随着横向挠度的增加，产生高水平的层间应力，响声也增大，由载荷-位移曲线可见对应的应变测点37处已经破坏，继而导致局部产生纤维脱层及层间剥离等多种损伤形式；继续加载至25.62 kN时，结构承载能力急剧下降，结构瞬间崩溃，最终结构失效的原因是口边应力集中区域表层纤维被挤压分层，导致结构承载能力急剧下降而瞬间崩溃破坏。

3 结 论

（1）本文进行了复合材料工字型梁腹板模型的剪切试验，数值仿真分析结果与试验结果相符合，表明运用“蔡吴失效准则”能够准确预测首层破坏载荷和破坏位置，并得到开口梁腹板的剪切失效模式是沿45°方向的口边层受压屈曲而局部产生纤维脱层及层间剥离等多种损伤形式。

（2）开口和补强对剪切载荷下复合材料工字型梁腹板稳定性的影响进行了量化研究。长圆形开口周边应力/应变集中现象显著，应变值为非开口区域的三倍以上；插层补强设计能有效地降低口边应力/应变集中程度，同时使结构稳定性承载力提高88%以及极限破坏载荷提高了46.3%。

（3）含开口和含补强的两种类型试件的破坏载荷分别是其屈曲载荷的2.11倍、1.59倍，说明本文所设计的复合材料工字型梁腹板充分发挥了该种结构的效能，而且补强设计有利于提高结构效率。

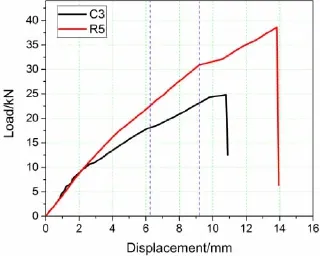
图12 试件加载的载荷—位移曲线Fig.12 Load-displacement responses of the I-section specimens