线路里程、偏距与坐标互算方法及其计算机实现

吴 坤 李 继

(林同棪国际工程咨询(中国)有限公司，401121，重庆//第一作者，高级工程师)

线路里程、偏距与坐标互算在轨道交通设计中经常遇到。线路专业经常需要把线路中心线周边一系列点提供给地勘单位进行钻孔勘探。待勘点由建筑、结构等专业确定。由于建筑、结构等专业制图比例并非1∶1 000，且不一定在原位制图，所以只能将待勘点以里程、偏距的形式提供给线路专业。而在线路敷设前期，地勘单位无法以里程、偏距放样，线路专业需将待勘点信息转化成坐标，以便勘探定位。同理，地勘单位返回的勘探结果以坐标表示点信息，线路专业需将其转化为里程、偏距形式反馈给各专业。

传统做法是线路专业将各专业提供的待勘点里程偏距信息绘制于图纸上，然后再一一查询坐标，填写表格；对于地勘单位返回的勘测结果，处理方式类似。线路专业需将待测点绘制在图纸上，然后量出对应的里程、偏距，填写表格。此过程工作量十分巨大，且极易出错。而国内主流轨道交通线路设计软件均无线路里程、偏距与坐标互算功能。因此，十分有必要开发一款线路里程、偏距与坐标互算的软件。

通过程序互算里程、偏距与坐标，无法借助于图形进行直观判断，传统基于图形的测量算法无法应用。本文结合轨道交通线路基本知识，借助解析几何手段和微分思想，着重研究线路里程、偏距与坐标互算的计算机算法。

1 基于待求点坐标的里程与偏距计算方法

无论已知线路里程、偏距计算点坐标还是已知点坐标计算里程、偏距，都必须已知线路数据。所谓线路数据是指线路的起点坐标、终点坐标、各交点坐标、各曲线半径、缓和曲线长和断链信息等。本文讨论的所有内容均建立在线路数据已知的基础上。

1.1 线路还原

线路还原是指通过已有的线路信息：起点坐标、终点坐标、交点坐标、曲线半径、缓和曲线长、断链等线路信息，计算出线路上每个直缓(或直圆)点、缓直(或圆直)点的坐标和里程。这样，线路被分成若干段，每一段只包含单一的直线或曲线，方便后面进行里程和偏距的计算。计算方法可以查找道路勘测设计相关的书籍，这里不作讨论。

1.2 待求点位置的判断

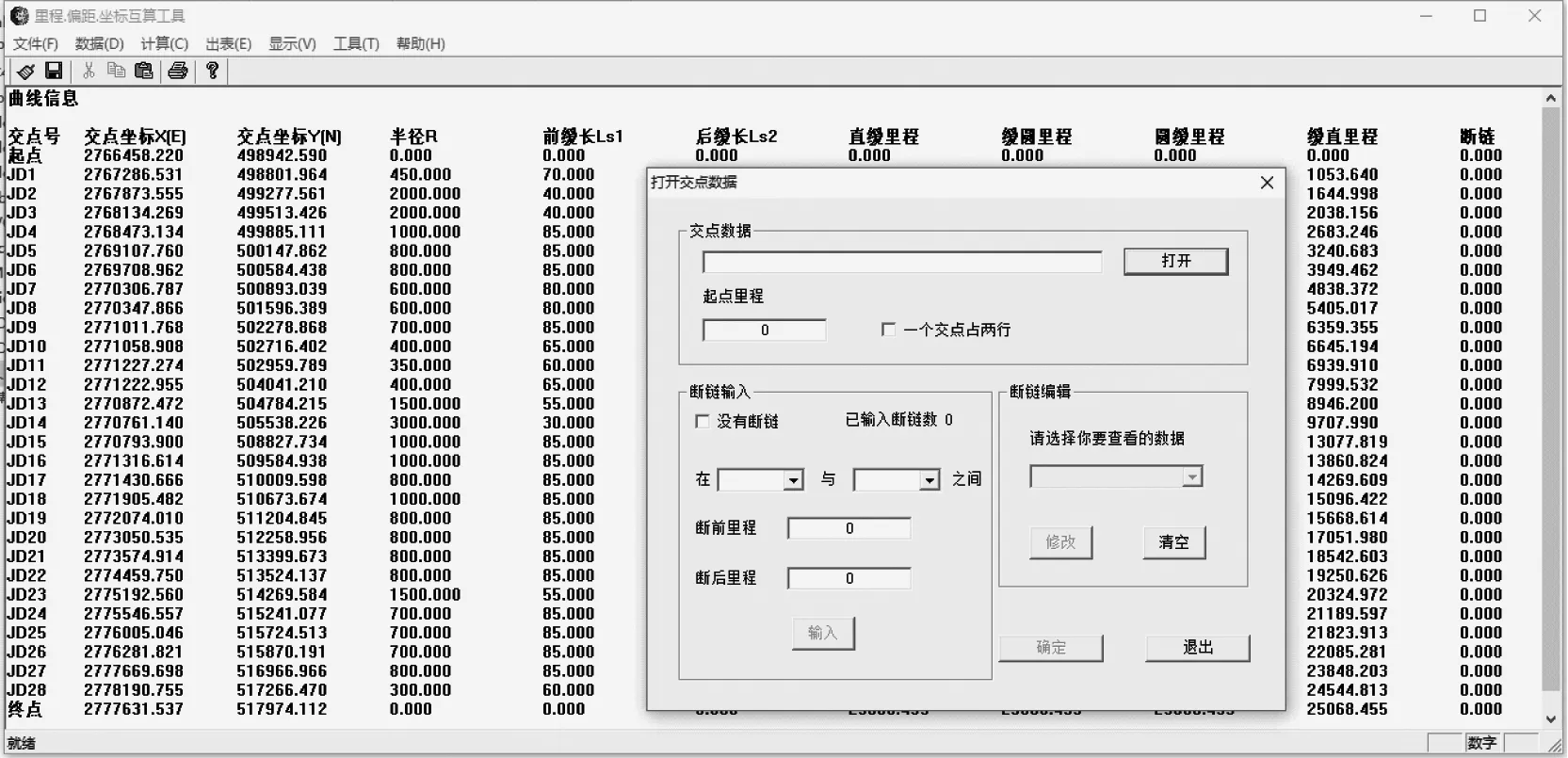
线路已分成单纯的直线或曲线段，为了计算方便且精确，首先判断点的投影在线路的哪一段直线或曲线上。

如图1所示，图中有一个待求点P和线路的3个直线段，分别是A段、B段、C段。P′为P点在线路上的投影。为了判断P点投影所在位置，用待求点P为顶点，3个直线段分别为对边做三角形，判断P点投影落在其中某一直线段上，图1中，P点投影落在B段直线上，则∠B1、∠B2均为锐角。

图1 待求点投影位置判断图(直线段)

用计算机计算时，先判断待求点是否落在线路直线段上。如果找到待求点投影落在某一直线段上，即终止计算，进行下一步计算。如果待求点投影没有落在直线段上，继续判断待求点投影是否落在曲线段上。

如图2所示，图中有待求点P和线路的2段曲线，分别是曲线M和曲线N。为确定待求点在哪一段曲线上，用待求点为顶点，以曲线为对边做扇形。计算扇形半径与曲线两端点处切线所形成的夹角，即图中的∠A2′与∠B1′。待求点投影落在A段直线和曲线M的交界位置时，∠A2=∠A2′=90°，待求点投影离开A段直线稍向曲线M移动微小距离d，都会导致∠A2′<90°。同理，待求点投影离开B段直线稍向曲线M移动微小距离d′，都会导致∠B1′<90°。由此可知，待求点投影落在某一段曲线上的充要条件是：该点与曲线形成的扇形半径与曲线两端点处切线所形成夹角为锐角。

图2 待求点投影位置判断图(曲线段)

需要说明的是，当待求点投影刚好落在直线与曲线的交点上时，既可以认为该投影落在直线上，也可以认为该点投影落在曲线上。为方便计算，本文将投影认定为落在直线段上。

1.3 待求点偏距和投影里程的计算

如果待求点投影落在直线段上，可以利用该点与直线段围成的三角形求解。如图3所示，三角形的3个顶点分别为：待求点P以及B1、B2，其中B1为缓直点(或圆直点)，B2为直缓点(或直圆点)。此两点的坐标已经在线路还原步骤中计算得出。利用余弦定理和射影定理，可以求解投影点P′距B1缓直点(或圆直点)的距离D和线段PP′的长度L，B1缓直点(或圆直点)的里程加上D即为待求点投影的里程，L即为待求点偏距。

如果待求点投影落在第n个曲线段上，需要先把曲线离散成散点，并计算出每一个点的坐标。离散精度根据工程需要设置，一般取1.0 mm或0.5 mm，精度设为d。曲线上各点坐标的计算方法成熟，此处不赘述。分别计算曲线离散点与待求点的距离，距离最小的曲线离散点即是待求点的投影点，最小距离即是待求点的偏距。设该离散点的顺序号为i，曲线起点里程为直缓点(或直圆点)，则待求点投影的里程可以表示为：直缓点里程+id(或直圆点里程+id)。

以某条1 km长的曲线为例，按1 mm为精度离散，离散点有1×106个，离散点坐标全部按双精度形存储，其占用内存为2×1×106×8字节，约15.2 M，在计算机硬件突飞猛进的今天，15.2M的内存对计算机运行不会造成明显影响。

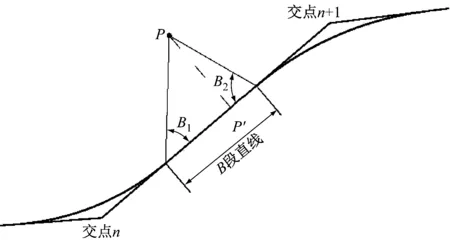
图3 偏距和投影里程计算图

1.4 待求点在线路左右侧的判定

当待求点投影落在直线段时，可以利用线路与某一基准线的夹角来判断待求点在线路的左侧或右侧，如图4所示。

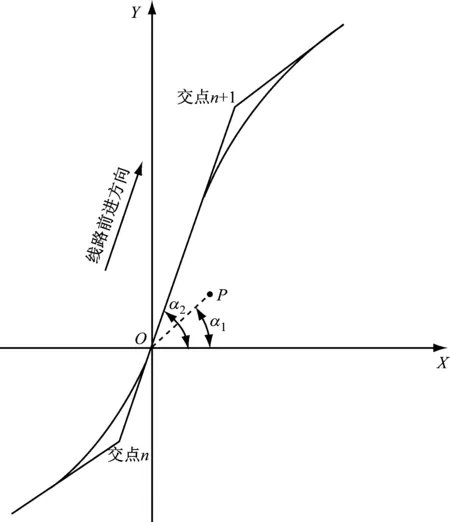
图4 待求点位置判定图(直线段)

图5 待求点位置判定图(曲线段)

2 基于里程与偏距的待求点坐标计算方法

已知里程与偏距计算该点坐标比较容易，除了知道待求点的里程与偏距外，还需要判断待求点处于线路前进方向的左侧还是右侧。

2.1 线路还原

线路还原的方法与作用同前文，此处不再赘述。

2.2 判断待求点投影所处位置

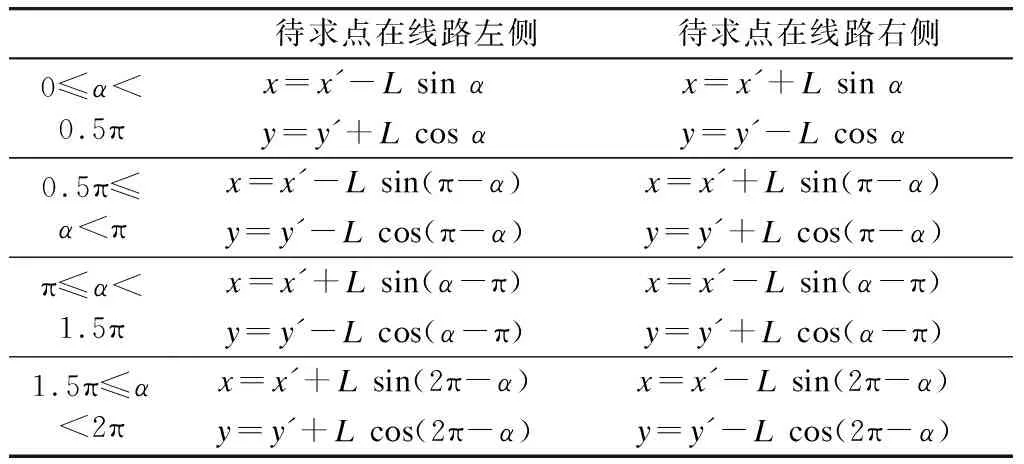
首先判断待求点投影在线路的直线段还是曲线段上，以便采取不同的计算方法。由于里程已知，通过待求点里程与直缓(直圆)、缓直(圆直)点的相对位置，即可轻松判断待求点投影位置。设待求点里程为H，若缓直点里程Hhz n(圆直点里程Hyz n)

2.3 待求点坐标计算

当待求点投影P′落在直线上时，设该段线路前一个交点的交点号为n。利用交点n的曲线末端点缓直点(或圆直点)和交点n+1曲线起端点直缓点(或直圆点)的坐标，求出线路前进方向与X轴正向夹角α，角度范围0～2π。具体求法参考平面解析几何，不在此文讨论范围。

偏距已知，设为L。角α取值范围不同，待求点位于线路左、右侧不同，待求点坐标表达式则不同。设投影点坐标为P′(x′,y′)，待求点坐标为P(x,y)，则有如表1所示的坐标关系表达式。

表1 待求点坐标表达式

化简表1中表达式，可得通用表达式，见表2。

表2 待求点通用坐标表达式

当待求点投影P′落在曲线上，其计算理论与已知坐标求里程和偏距时，与待求点投影P′落在直线上的计算理论相类似，不再赘述。

3 断链的处理

若线路中含有断链，计算里程、偏距和坐标时要受到断链影响。断链主要有长链和短链两种。断前里程大于断后里程时为长链，断前里程小于断后里程时为短链。其中长链具有重复里程。

3.1 断链数据信息

当线路中存在断链时，计算必须加入断链信息。断链主要信息为断前里程与断后里程。为方便计算机计算，可在录入断链的同时录入断链所处的交点区间。一般情况下，断链全在直线上，且断链影响范围内不会再出现断链时，此处可以不考虑断链在曲线上和断链重叠的情况。当线路中存在长链时，若是已知里程、偏距求坐标的待求点刚好在断链影响范围内，则该待求点里程存在两种可能性。录入已知条件时，需要录入该待求点里程是否为长链的重复里程。

3.2 基于待求点坐标计算线路里程与偏距时的断链处理

首先不考虑断链，用第1节介绍的方法求出里程与偏距，其中只有里程受到断链影响。设不考虑断链求出的里程为H，最终里程为Ht，H所处的直线段前一个交点为交点n。把里程H与交点n以前的所有断链长度做代数和，求出H′。若H′所处直线段无断链，则H′=Ht；若H′所处直线段有断链，需再判断H′是否在本段直线上的断链的影响范围内。若在，与断链长度做代数和得出Ht；若不在，H′=Ht。设断前里程为Dq,断后里程为Dh，可得以下公式：

式中：

Dqi——第i个断链的断前里程；

Dhi——第i个断链的断后里程；

Dqn——第n个断链的断前里程；

Dhn——第n个断链的断后里程。

3.3 基于待求点里程与偏距计算该点坐标时的断链处理

首先，不考虑该已知里程H为长链重复里程，求出真实里程H′。若该点是长链重复里程，在H′基础上加上长链长度即为真实里程。

4 成果应用

通过上文的研究，得出线路里程、偏距与坐标互算的新算法。此算法脱离了图形，采用了全数字计算方式，使得计算机实现成为可能。

基于研究成果，笔者以VC++为例，实现了线路里程、偏距与坐标互算程序。该程序可以实现里程、偏距与坐标的互算，支持Excel导入基本数据和计算结果导出Excel。经大量工程验证，该程序完全满足工程精度要求，且大大提高了工作效率。以笔者曾经就职的设计院为例，该程序可以在10 min内完成原来1～2 d的工作，深受好评。

图6和图7展示了程序界面与计算成果。

图6 程序界面

图7 计算成果输出