基于ANSYS WORKBENCH的六自由度工业机器人摆动臂静力学分析与模态分析

陈继文

（山西机电职业技术学院，长治 046011）

0 引言

六自由度机器人运动灵活，在码垛、搬运、焊接、装配、喷涂等场合有着广泛的应用。为了保证机械臂运行的可靠性，需要对其进行机械结构分析。使用实验方法验证机器人结构设计的合理性，成本高，周期长[1]，传统静力学计算方法精度低，过程繁琐。本文使用Pro/E软件建立并简化六自由度机器人模型，利用ANSYS对摆动臂进行静力学分析，得到了摆动臂的应力和应变分布云图，有效的提高了精度，降低了周期，节约了成本。模态分析可以用来研究结构动力学特性。本文依据数值模态分析理论，使用有限元分析方法得到了六自由度机器人的六阶模态振动特性，得到了各个部件的固有频率和振型，为机器人结构优化设计和改进提供了理论依据，为设计同类产品提供了借鉴。

1 六自由度机器人摆动臂有限元模型建立

1.1 建立几何模型

六自由度机器人由底座、旋转座、摆动臂、摆动关节、旋转臂、腕关节组成。整机构造复杂，需要根据等效刚度代换理论对模型做简化处理[2]。把齿轮啮合简化为孔和轴的配合，忽略固定构件、线路、电位器、外部柔性导线管等对计算机分析影响不大的特征和部件，将质量等效分布，结构中相同材料的刚性作一体化处理[3]，机器人模型如图1所示。

图1 六自由度工业机器人模型

1.2 定义模型材料属性及网格划分

HT250耐磨性、减震性好，ZL108气密性高，线收缩较小，热膨胀系数低，六自由度机器人安装底座使用HT250灰铸铁，旋转座、摆动臂、摆动关节与旋转臂均采用ZL108材料，材料属性如表1所示。使用ANSYS WORKBENCH网格划分工具对摆动臂进行网格划分，网格划分情况如图2所示，六自由度机器人摆动臂的网格节点数为65972，网格单元数为87150。

表1 机器人摆动臂材料属性

图2 机器人摆动臂网格划分结果

2 六自由度机器人摆动臂静力学分析

2.1 施加载荷

当机器人摆动臂和旋转臂均处于水平位置时，末端执行器的位移量最大，在该位置姿态下对六自由度机器人进行应力分析。以荷重0kg为例，摆动臂竖直方向受到机器人摆动关节、旋转臂、腕关节的作用，总质量12.939kg，力的大小为126.802N，端面面积为0.0076969m3，产生的压力为0.01647MPa，在Pro/E中测得力的作用点距离摆动臂端部沿臂展方向的距离为111mm，产生14075 N·mm的力矩，摆动臂上载荷情况如表2所示。

表2 机器人摆动臂载荷大小

2.2 应力分析

载荷和约束施加到摆动臂上后，进行求解，得到摆动臂在0～5kg荷重下的应力分布云图3和应力大小表3。

图3 摆动臂在0～5kg荷重下的应力分布云图

表3 摆动臂在0～5kg荷重下的应力大小

表4 摆动臂在0～5kg荷重下的应变

从图3和表3可以看出，摆动臂在无荷重时，等效应力为0.98704MPa，荷重5kg时，应力达到1.4793MPa，该应力远远小于ZL108的屈服极限177MPa，满足要求。同时，随着机器人荷重的增加，最大应力随之增大，但最大应力发生的位置基本保持不变，位于摆动臂与旋转座连接处圆形端面的右侧边缘部位。

2.3 变形分析

载荷和约束施加到摆动臂上后，进行求解，得到摆动臂在0～5kg荷重下的总形变位移分布图4和应变大小表4。

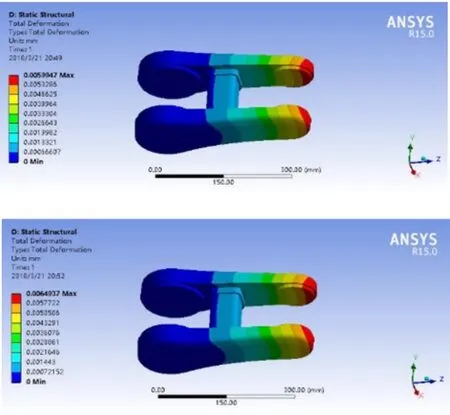
图4 摆动臂在0～5kg荷重下的总应变分布云图

从图4和表4可以看出，无荷重时，六自由度机器人摆动臂的形变量为0.0040106mm，荷重5kg作用下，最大形变量为0.0064937mm，符合要求。同时，随着机器人腕部荷重的增加，最大应变量随之增大，但最大应变发生的位置基本保持不变，位于摆动臂右侧顶端位置。

3 六自由度机器人摆动臂模态分析

六自由度机器人摆动臂无预载荷状态下1～6阶振型模态分析结果如图5所示，频率和变形量如表5所示。

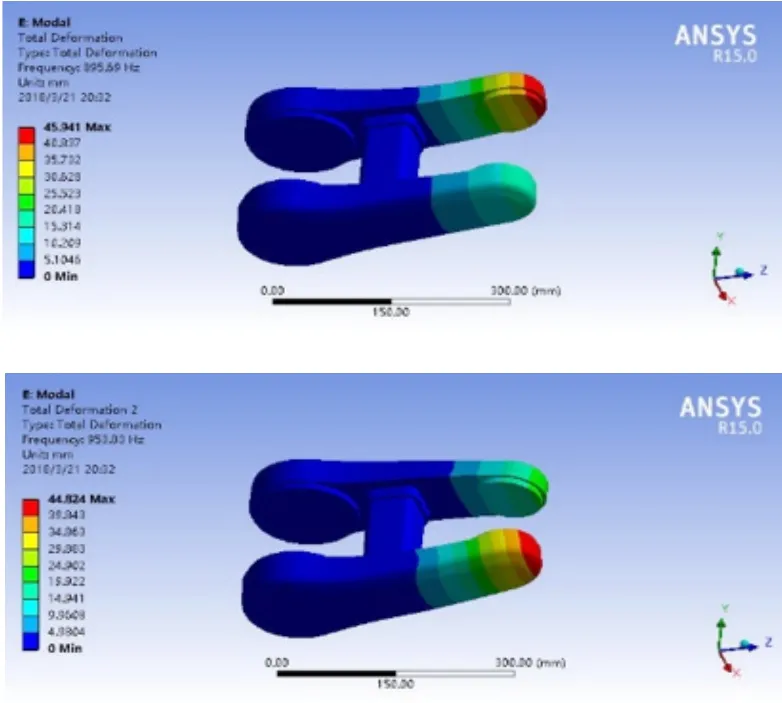
表5 无预载荷状态下前6阶固有频率和变形量

图5 无预载荷状态下前6阶振型图

根据图5和表5可知，前6阶振型中，固有频率最低为895.69Hz，最高为3138.0Hz；第5阶的最大变形量最小，为26.299mm，摆动臂前端沿着z轴方向左右振动；第6阶的最大变形量最大，为56.874mm，摆动臂前端左臂绕着z方向顺时针旋转。运动机构伺服电机的额定转速是3000r/min，频率是50Hz，本模型摆动臂自身的刚度满足要求，相对较为薄弱的部分是与摆动关节接触的端部边缘。

4 结论

1）利用Pro/E的三维建模和质量属性测量功能，通过计算，完成了摆动臂的质量、质心、坐标的测量，并得到摆动关节、旋转臂、腕关节等在摆动臂上的载荷大小、方向和作用位置，避免了繁琐的实物测量过程和测量带来的误差。

2）提出了使用ANSYS WORKBENCH对六自由度机器人静力分析，得到了摆动臂的应力云图和形变位移分布图，完成了强度和变形量的校核，六自由度机器人的危险位置在摆动臂与旋转座连接处圆形端面的右侧边缘和摆动臂右侧顶端。

3）研究了不同荷重对机器人摆动臂刚度的影响，随着机器人腕部荷重的增加，最大应力随之增大，应变也随之增大，但最大应力和最大应变出现的位置基本保持不变。

4）完成了机器人摆动臂模态分析，实现了摆动臂的结构动力学分析，机器人在工作中应该避开危险频率，避免共振现象的发生，找到了机械结构的薄弱环节，为六自由度机器人的设计优化及驱动选型提供了依据。