中承式蝴蝶形系杆拱桥受力性能分析

詹刚毅，彭跃辉，陈梦成，杨 超

(1.南昌铁路勘测设计院有限责任公司，江西 南昌 330002；2.华东交通大学 土木建筑学院，江西 南昌 330013)

蝴蝶形系杆拱桥是近年来兴起的新型拱桥，具有受力合理、整体性好、造型美观等优点，应用前景良好。中国第一座下承式蝴蝶形系杆拱桥——天津大沽桥[1]、第一座中承式蝴蝶形系杆拱桥——无锡兴塘大桥[2]分别于2005,2006年建成通车。

中国现有的部分蝴蝶形系杆拱桥及其相关设计参数，见表1。由表1可知，拱肋的倾角在10°～45°，拱肋倾角的变化对主要构件的受力有较大影响[3]，由于其拱肋外倾，连接主梁的拉索产生水平、竖直方向上的分力引起拱顶横位移，与普通的系杆拱桥相比较，拱肋横向位移问题较为突出，稳定性问题亦是此类桥型设计重点考虑因素[4]；而且，外倾拱肋不仅受压弯作用，还承受平面外扭矩，受力行为空间效应明显，这也是此类桥型的主要特征[5-7]。

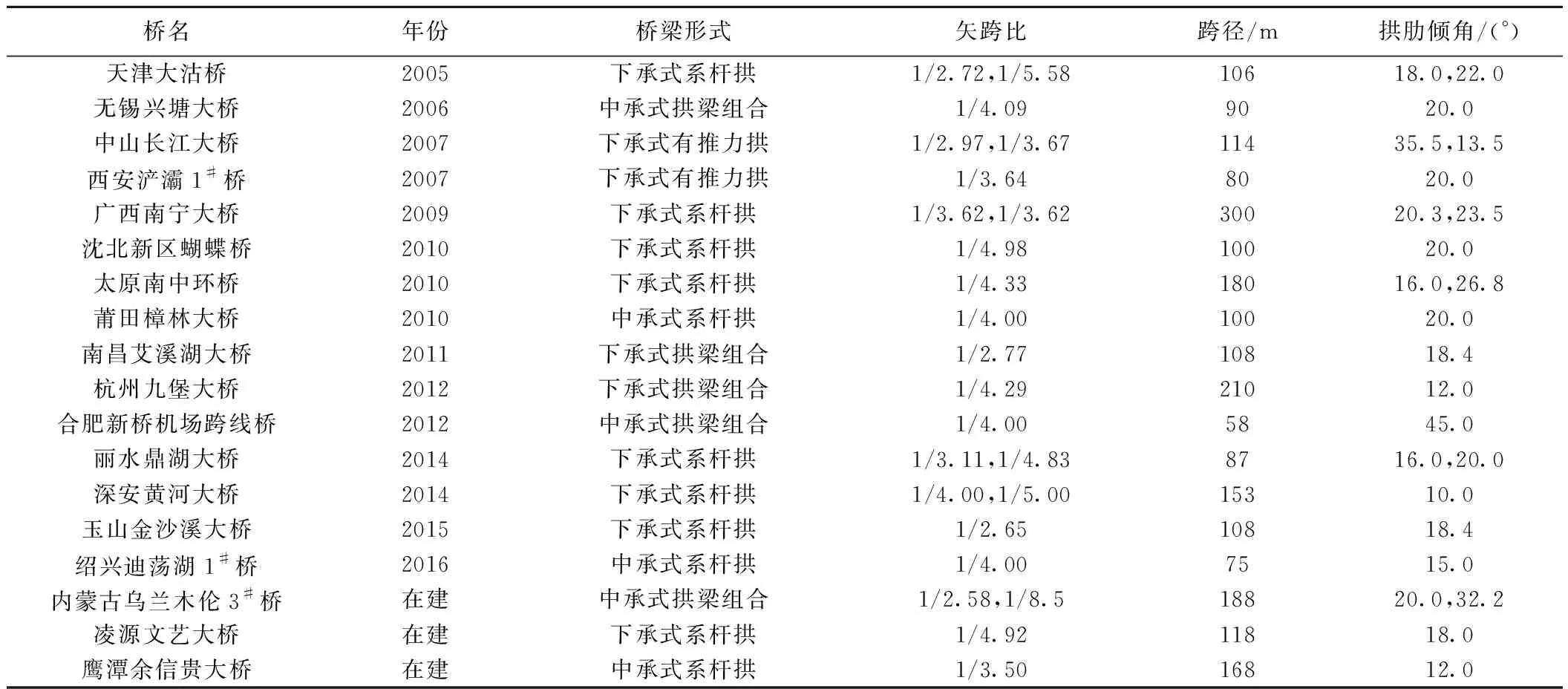
表1 我国部分现有蝴蝶形系杆拱桥

蝴蝶形系杆拱桥问世以来，国内有关学者针对其典型受力特征开展了相关研究。谷利雄[8]利用ANSYS有限元软件建立了中山长江大桥有限元模型，并对其进行稳定性分析，分析结果表明：桥梁的稳定性的主要与桥宽、横向联系有关。失稳时，先内、外拱顶向外倾斜发生失稳，并随着拱肋倾角的增大，稳定安全系数不断降低。刘彬斌[9]以南宁大桥为背景，建立三维全桥杆系模型进行整体稳定性计算并选取西拱肋中部分节段进行局部稳定计算，分析结果表明：局部失稳对结构的第一类稳定起控制作用，在稳定分析中必须考虑局部稳定的影响，而结构的极限承载状态由整体稳定控制。苏庆田[10]以南宁大桥为背景对全桥进行了弹性稳定分析，结果表明：对于薄壁箱形截面构件采用有限元方法计算偏于不安全，必须考虑其局部稳定的影响。傅金龙等[11]以艾溪湖大桥为背景建立空间有限元模型，对该桥在成桥状态下和吊杆张拉施工过程中的结构稳定性进行分析，分析结果表明：该桥的失稳模态主要表现为拱肋平面外失稳；几何非线性和材料非线性、吊杆张拉方式、拱肋矢跨比、外倾角、截面刚度等参数对该桥稳定性有不同影响。罗慧苓[12]基于中国现有蝴蝶形拱桥的统计结果，以余信贵大桥为研究对象，研究了拱肋外倾对桥梁稳定性能的影响，结果表明：余信贵大桥失稳模式表现为平面外失稳，且结构横向稳定问题突出。

由于蝴蝶形系杆拱形式多样，造型多变，每座蝴蝶形系杆拱均有各自的受力特点。本文以蝴蝶形系杆拱桥——余信贵大桥为研究对象，开展其施工阶段和成桥整体受力性能分析，为今后类似蝴蝶形系杆拱桥的设计和施工提供借鉴。

1 工程背景

鹰潭市余信贵大桥位于信江新区与余江县中童镇之间的信江河段上。主桥结构形式(48+168+48)m为中承式蝴蝶形钢箱拱肋混合梁系杆拱桥。主拱拱肋跨径168 m，矢高48 m，矢跨比为1/3.5，主桥主跨桥面宽为33.5 m，设计荷载为城-A级。余信贵大桥的桥型总体布置，见图1。

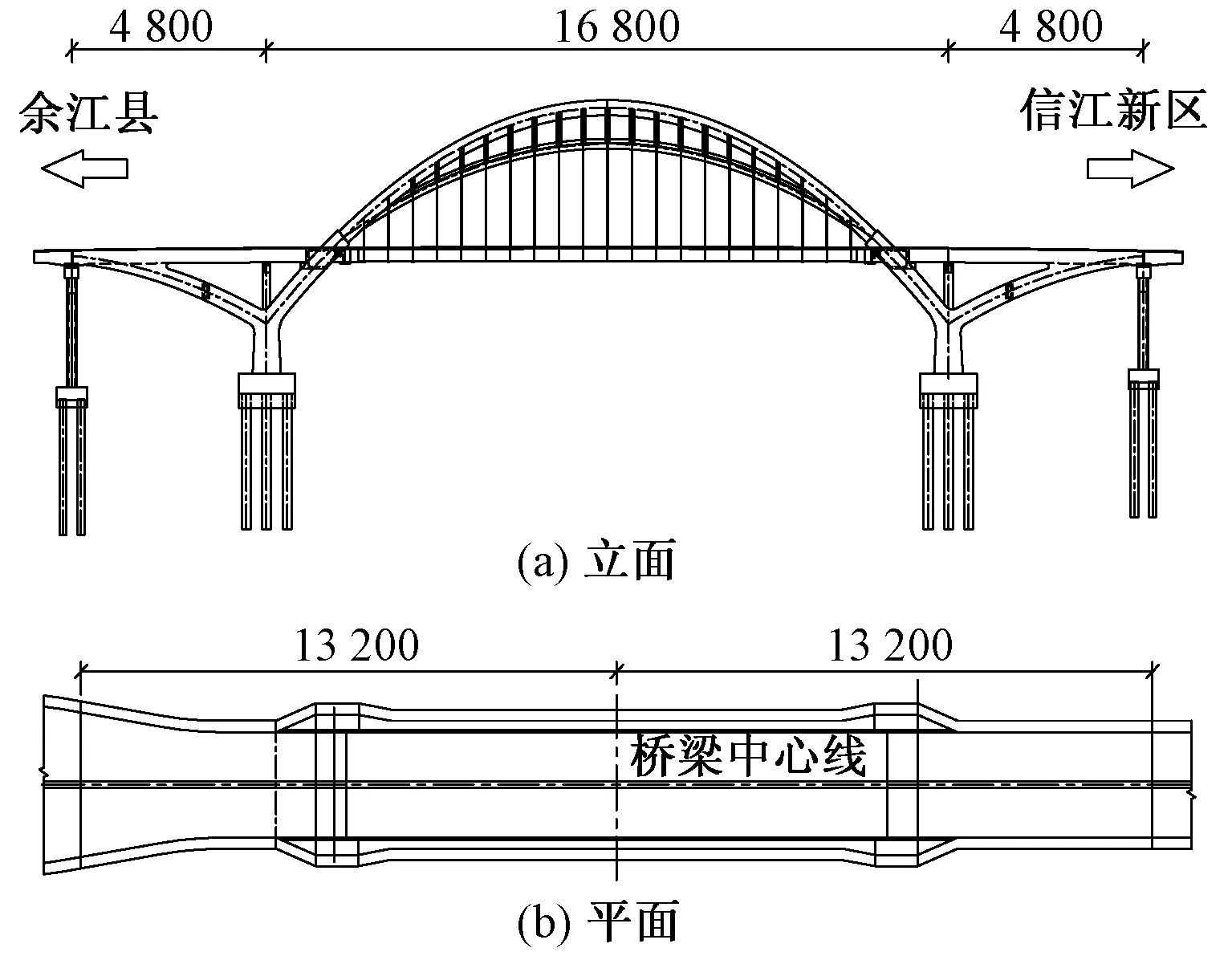
图1 余信贵大桥整体布置(单位：cm)

2 有限元模型建立

采用桥梁计算软件MIDAS/Civil，建立空间计算模型，见图2。除吊杆及系杆采用桁架单元模拟，桥面板采用板单元模拟外，其余构件均采用梁单元模拟。不考虑桥面铺装的抗弯刚度，桥面铺装及桥面附属设施等均考虑其重量。模型共有 2 376 个节点，3 304 个单元。其中，梁单元 2 618 个，桁架单元62个，板单元624个。有限元模型分成32个施工阶段。

图2 全桥有限元计算模型

图3 施工及运营阶段主拱肋应力

因余信贵大桥设计于2014年，JTG D60—2015《公路桥梁设计通用规范》与JTG D64—2015《公路钢结构桥梁设计规范》尚未施行，因此有限元模型仍按照JTG D60—2004《公路桥涵设计通用规范》[13]与JTJ 025—86《公路桥涵钢结构及木结构设计规范》[14]进行大桥施工阶段、运营阶段受力性能计算。

3 主要构件受力性能分析

3.1 拱肋

3.1.1 主拱肋

最不利施工阶段和承载能力极限状态下，主拱肋上下缘正应力及剪应力见图3。可见，在施工阶段和承载能力极限状态下，主拱肋上下缘正应力及剪应力均未超过Q345钢材截面抗压强度设计值-200 MPa、抗拉强度设计值200 MPa和抗剪强度设计值120 MPa，即主拱肋满足承载能力极限状态验算要求。

3.1.2 副拱肋

在施工和运营阶段，副拱肋上下缘正应力及剪应力见图4。可见，在承载能力极限状态下，副拱肋上下缘正应力及剪应力均未超过Q345钢材截面抗压强度设计值-200 MPa、抗拉强度设计值200 MPa和抗剪强度设计值120 MPa，即副拱肋满足承载能力极限状态验算要求。

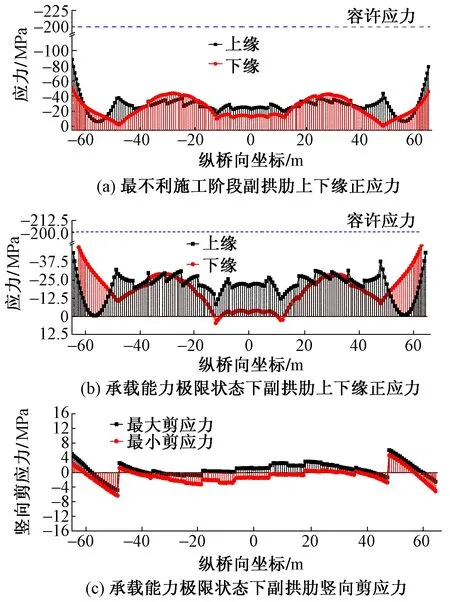
图4 施工及运营阶段副拱肋应力

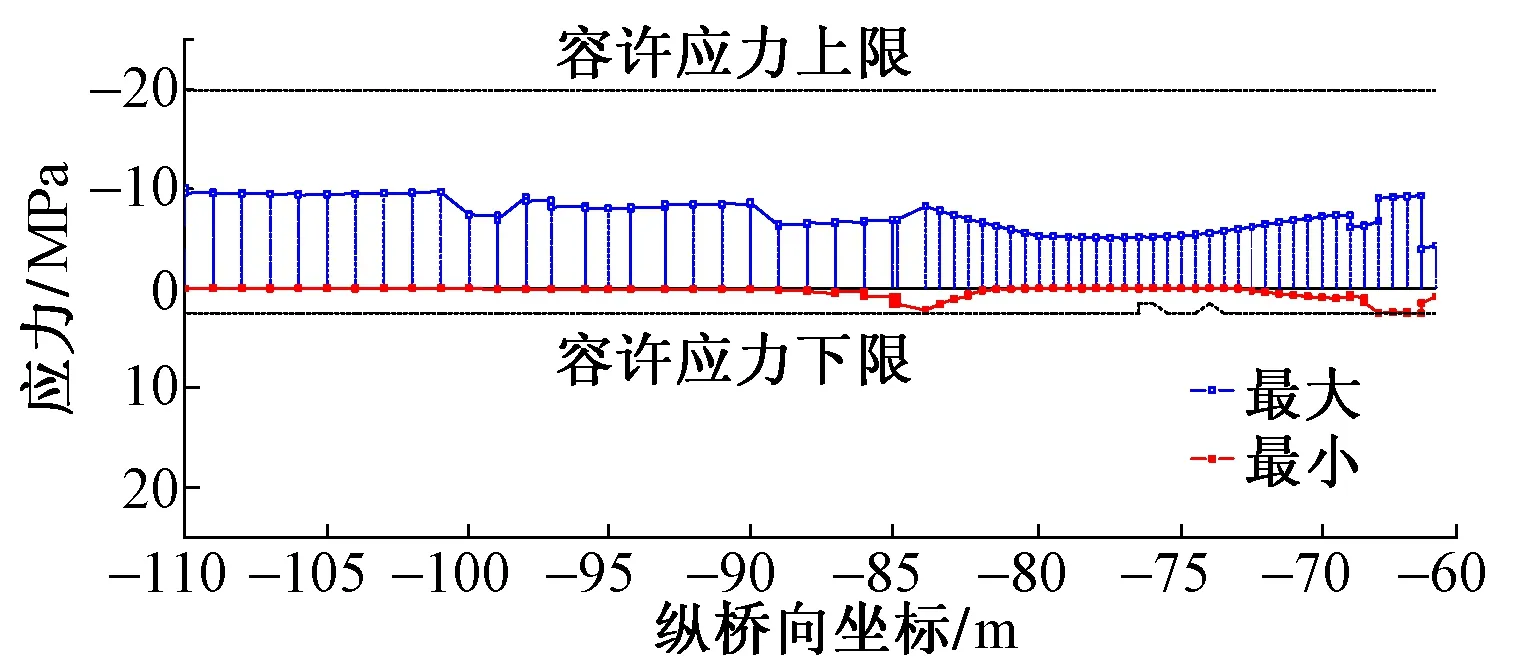
图5 施工阶段三角刚架法向压应力

3.2 三角刚架

施工阶段三角刚架法向压应力见图5。可见，施工阶段三角刚架法向压应力满足要求。在承载能力极限状态下，三角刚架混凝土拱肋验算结果见图6。可见，混凝土拱肋正截面抗弯验算、斜截面抗剪验算、正截面压应力验算满足要求，V腿与边跨主梁交接位置处正截面抗裂验算及斜截面抗裂验算均不满足要求。由于三角刚架域构造复杂，采用杆系模型模拟精度可能不够，该区域实际的应力分布情况进行局部实体有限元分析，并以其分析结果为准。

图6 承载能力极限状态下三角刚架混凝土拱肋验算结果

3.3 主纵梁

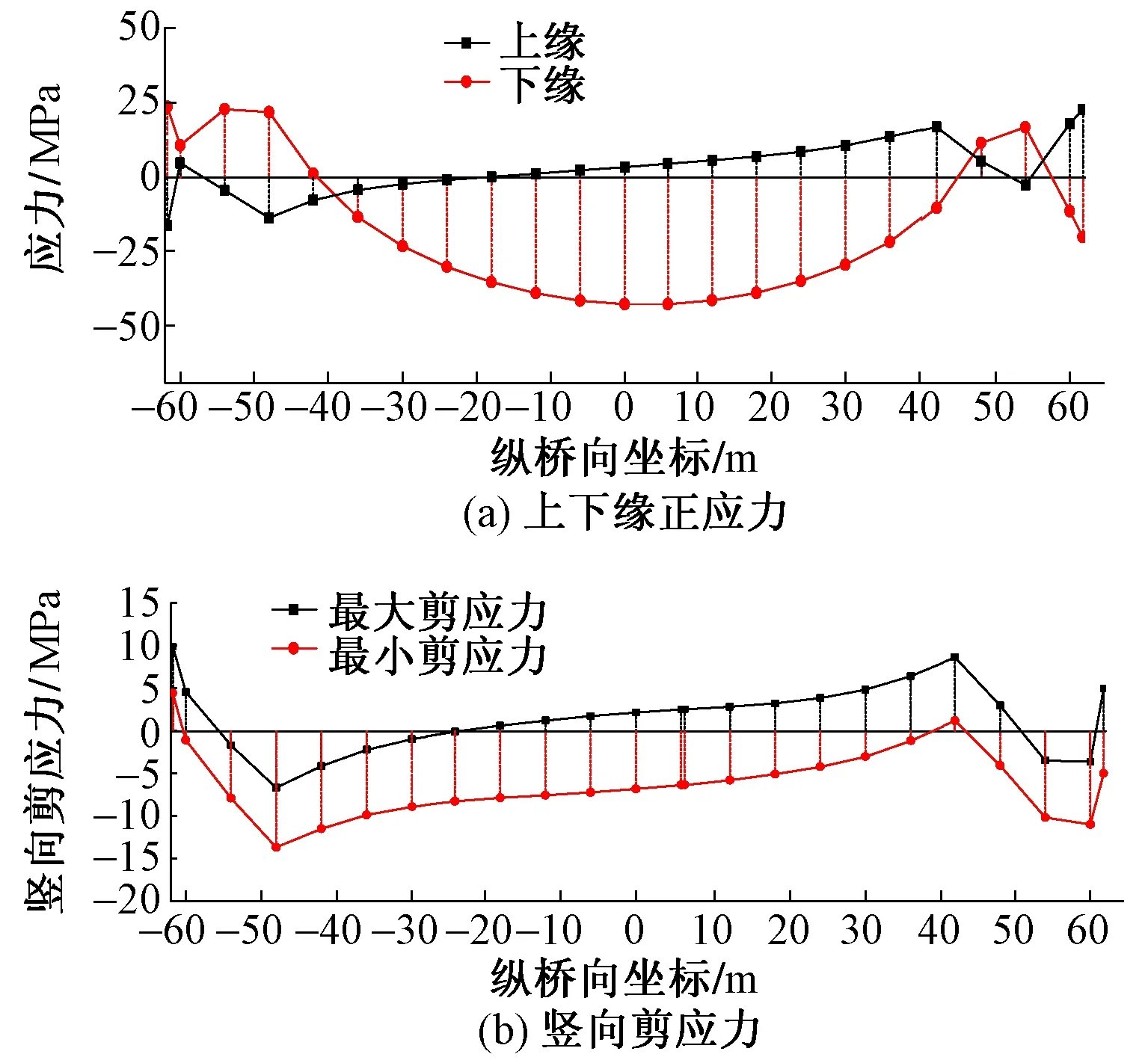
图7 承载能力极限状态下主纵梁应力

因施工阶段主纵梁受力较小，因此本文仅给出承载能力极限状态下主纵梁上下缘正应力及剪应力，见图7。可知，在承载能力极限状态下，主纵梁上、下缘正应力及剪应力均未超过Q345钢材抗压强度设计值-200 MPa，抗拉强度设计值200 MPa和抗剪强度设计值120 MPa，即主拱肋满足承载能力极限状态验算要求。

3.4 系杆和吊杆

系杆和吊杆参照JTG/T D65-01—2007《公路斜拉桥设计细则》[15]中拉索的设计方法进行验算，即拉索应力不应大于其容许应力Ryb的0.4倍。

余信贵大桥系杆包括通长系杆、边跨系杆和中跨系杆3类。通长系杆、中跨系杆和边跨系杆分别采用8孔55束7φ5、4孔27束7φ5和4孔55束7φ5钢绞线。根据使边跨混凝土拱肋和主跨钢拱肋受力合理并平衡拱肋水平推力的原则，在各施工过程和成桥运营阶段，通长系杆、中跨系杆及边跨系杆的最大张拉力分别为 33 093，3 789，2 947 kN，其安全系数分别为3.4，7.3，19.0，满足要求。

在运营阶段的承载能力极限状态下吊杆轴力最大，但所有吊杆的安全系数均不小于3.3[16]，满足要求。

3.5 结构刚度

在车道荷载和人群荷载作用下，主、副拱肋挠度及主纵梁挠度见图8。由图8(a)可知，主、副拱肋挠度最大值均出现在约-30 m处，大小分别为39.8，40.3 mm，均小于L/800(L为跨度)，故主、副拱肋刚度满足要求。由8(b)可知，主纵梁各点挠度差最大值47.2 mm出现在-30 m处，小于L/600，故主跨主梁刚度满足要求。

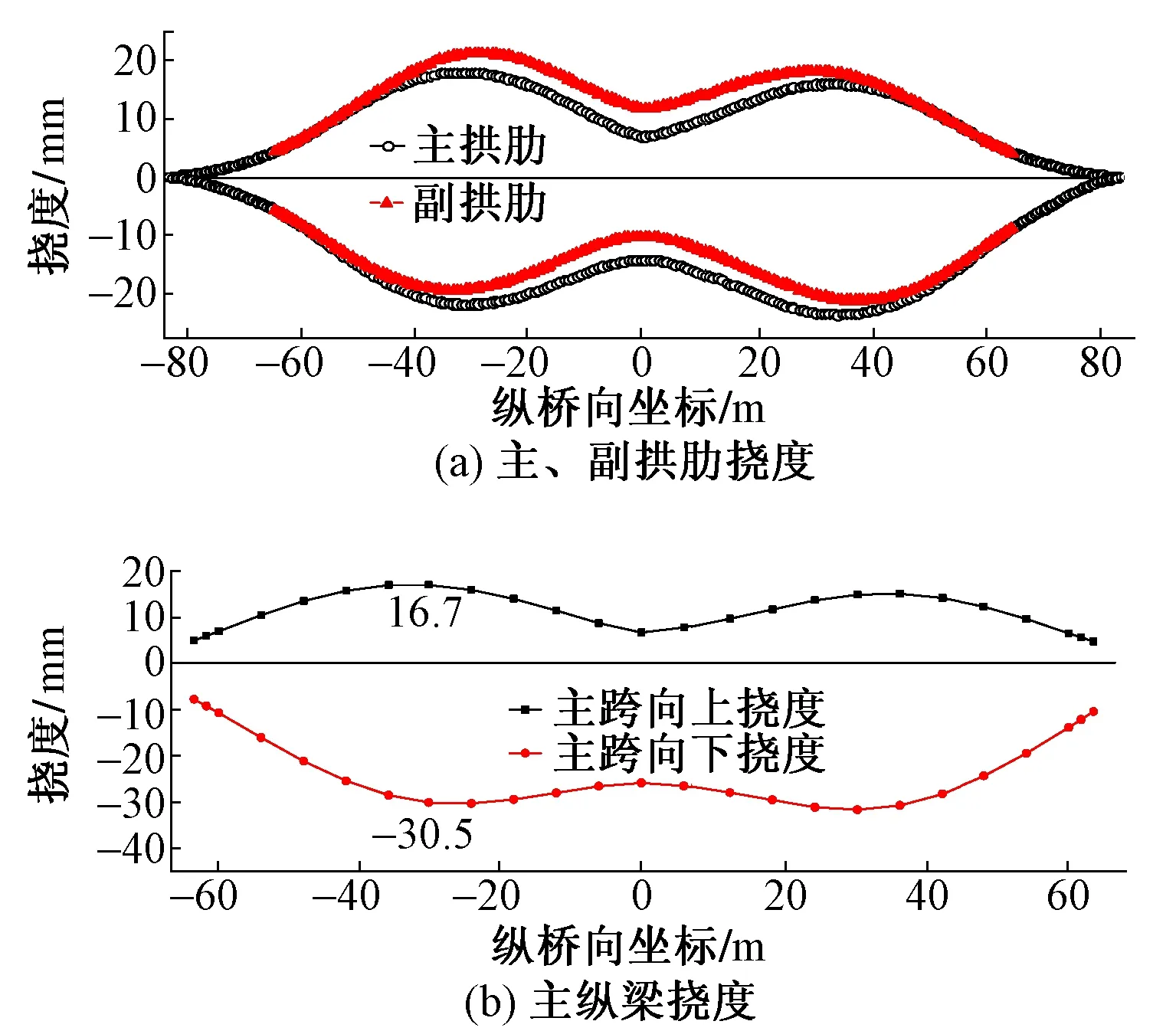
图8 移动荷载作用下主、副拱肋及主纵梁挠度

4 全桥稳定性分析

稳定计算采用第一类线弹性稳定计算方法，控制方程为

根据计算方程式(1)，可将稳定问题转化为求方程的最小特征值问题。

对于车道、人群等可变荷载，根据拱脚推力影响线在主梁上以静力荷载的形式进行布置，使拱脚水平推力最大。

余信贵大桥在恒载及荷载组合作用下的弹性一阶失稳模态均表现为平面外反对称失稳，见图9。稳定系数分别为15.64，13.03，均大于GB 50923—2013《钢管混凝土拱桥技术规范》[16]规定的弹性稳定特征值 4.00，满足要求。

图9 一阶失稳模态

5 结论

1)在施工阶段和承载力能力极限状态下，主拱肋、副拱肋以及主纵梁正应力小于容许应力200 MPa，剪应力小于120 MPa，满足要求。

2)在施工阶段的承载能力力极限状态下，三角刚架混凝土拱肋正截面抗弯验算、斜截面抗剪验算、正截面压应力验算满足要求，但V腿与边跨主梁交接处正截面抗裂验算及斜截面抗裂验算不满足要求。由于三角刚架处构造复杂，采用杆系模型模拟精度存在不足，因此该区域实际的应力分布情况应采用局部实体模型或试验模型进行研究。

3)通长系杆、中跨系杆和边跨系杆的安全系数分别为3.4，7.3，19.0，吊杆的安全系数均不小于3.3，满足要求。

4)在移动荷载作用下，主、副拱肋挠度分别为39.8，40.3 mm，均小于L/800，主纵梁最大挠度差为47.2 mm，小于L/600，故主、副拱肋及主纵梁刚度满足要求。

5)在恒载及荷载组合作用下，余信贵大桥弹性一阶失稳模态均为平面外反对称失稳，稳定系数分别为15.64，13.03，均大于4.00，满足要求。