基于实时中值估计的分布式稳健滤波融合方法

黄 河，陈庆良，张 旭

(中国洛阳电子装备试验中心，河南 洛阳 471000)

0 引言

在电子信息装备多源测量数据融合处理工作中，通常会遇到复杂电磁环境造成的连续粗差。这时，基于白噪声假设的传统方法往往表现不好，需要研究数据融合的稳健方法。

关联、配准、检择、滤波、加权是数据融合中相互联系、相互影响的几个过程，相关的处理方法直接关系到最终的数据质量，本文主要关注其中的稳健滤波、稳健加权问题。对此，很多文献进行了讨论，提出了许多不同方法。魏喜庆等[1]将高斯过程回归引入到容积卡尔曼滤波之中，文献[2—4]也介绍了一些稳健滤波方法，但却均未对样本崩溃点进行分析。加权融合方面，文献[5—8]将权值最优分配原则与卡尔曼滤波结合应用，但未考虑稳健性问题；文献 [9]采用M估计实现参数稳健估计和权值最优分配原则下的加权融合，但只适用于静态数据融合，未讨论运动目标测量数据的稳健滤波融合方法。

本文针对电子信息装备运动目标多源测量数据加权融合中的复杂电磁环境影响，在以往工作[10-12]的基础上，研究提出了基于实时中值估计的分布式稳健滤波融合方法。

1 权值最优分配原则应用中的问题

1.1 融合权值最优分配原则

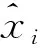
令加权因子分别为W1，W2，…，WS，则

(1)

可知总均方误差为：

(2)

可见，总均方误差是关于各加权因子的多元二次函数，因此必然存在最小值。根据多元函数求极值理论，可求出总均方误差最小时所对应的加权因子为：

(3)

则有

(4)

其对应的最小均方误差为：

(5)

1.2 问题提出

电子信息装备多源测量数据融合处理中，在应用上述精度构建融合权重的权值最优分配原则时，由于动态测量中设备精度的不平稳性，以及没有绝对意义上的真值，需要对设备精度进行动态的近似估计，从而进行自适应的加权融合。这种情况下，由于常用的标准差形式的精度估计方法不具备稳健性，以及复杂电磁环境下粗差的影响，需要研究稳健的滤波方法和稳健的精度估计方法。

本文构建了一种高样本崩溃点的稳健滤波方法，并用稳健滤波残差刻度估计作为动态精度构建融合权重，从而实现稳健的自适应加权融合，这里称作稳健刻度法。

2 基于实时中值估计的稳健滤波方法

2.1 中值估计的稳健性

中值(中位数)估计是一种基本的稳健估计方法。对采样序列yi，其中值为：

(6)

式(6)中，y(j)表示对数据{y1,y2,…,ym}按从大到小排序后的第j个数值。

中值估计是按极小化极大准则的一种最优估计，其影响函数有界，样本崩溃点接近50%，因此中值估计有良好的稳健性，可以提供工程应用中十分重要的高样本崩溃点这一性质。因此，本文研究提出以下基于实时中值估计的稳健递推滤波方法。

2.2 基于双向链表排序的实时中值估计算法

由于中值估计需要对采样序列进行排序，作者从节省内存、减少运算的角度出发，在考虑了数组、单链表、双向链表、队列等数据结构后，选定带顺序号索引的双向链表作为算法实现的基本数据结构，排序算法选用插入排序，因为它更适合向有序表中添加元素。

应用中应先对双向链表进行相应声明，创建、初始化头节点，并根据实际需要设定双向链表节点数目。节点删除时，应依据先入先出的原则，按照插入顺序索引寻找应删除的节点；节点插入时，按照x值大小进行排序，并对相应节点(新节点及大小顺序发生变化的原有节点)的大小顺序索引进行赋值。排序完成后，即可得到中值。实时中值估计主要算法流程如图1所示。

2.3 稳健滤波

2.3.1预测

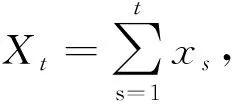
(7)

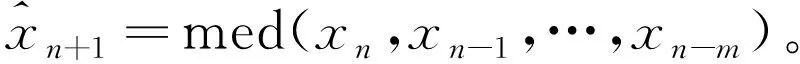
(8)

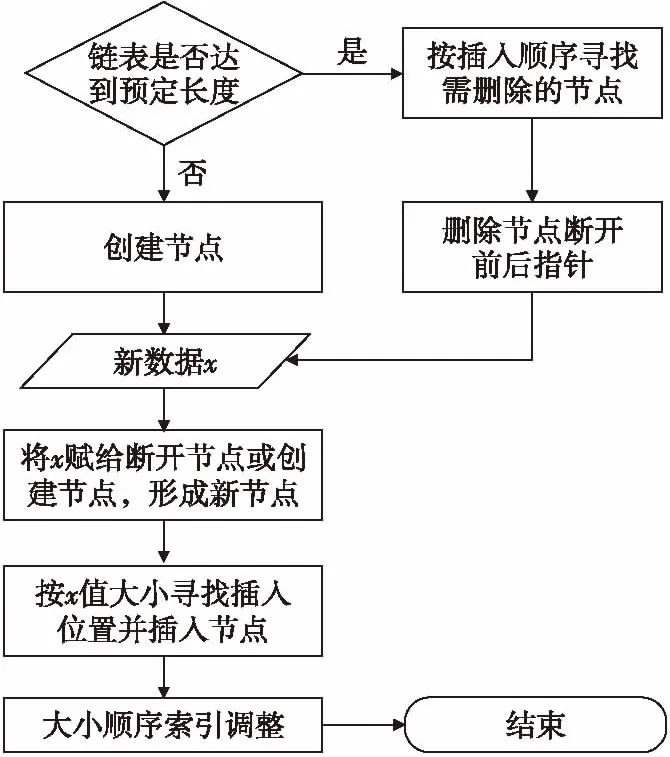
图1 排序双向链表节点插入与删除算法流程图Fig.1 The main flow for inserting and deleting node of the ordered doubly-linked list

2.3.2滤波

(9)

(10)

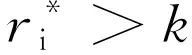
(11)

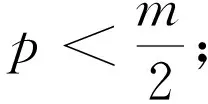
至此，对匀速直线运动，我们构造了基于一阶差分及其误差刻度中值估计的实时稳健滤波方法，它实际上共包含三重中值估计，因而是一种高样本崩溃点的稳健递推滤波方法。对于匀加速直线运动，可以应用类似的方法用二阶差分构造相应的稳健滤波。

实际应用中还应考虑目标机动对算法的影响，据参考文献[13],目标缓慢转弯往往引起长达1 min的相关加速，目标作躲避机动时的相关加速时间为10～30 s，而由大气湍流或飞机自身随机因素引起的相关加速度时间只有1～2 s。综合起来考虑，为避免将机动当作干扰处理，算法的设计样本容量在时间尺度上应不超过2 s。

3 融合方法及算法流程

3.1 分布式融合方法

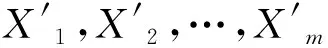
(12)

3.2 算法流程

在工程应用中，稳健滤波融合方法中的实时中值估计和系统误差配准[11]均可应用上述基于双向链表排序的实时中值估计算法(见2.2节)。图2为基于实时中值估计的稳健滤波算法流程。

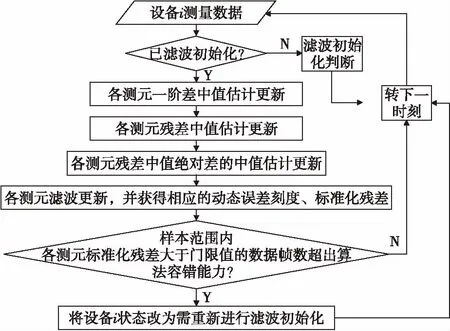
图2 基于实时中值估计的稳健递推滤波算法流程Fig.2 The robust filtering algorithm based on real time median estimation

图3为基于稳健滤波残差刻度估计的分布式自适应加权融合算法流程。

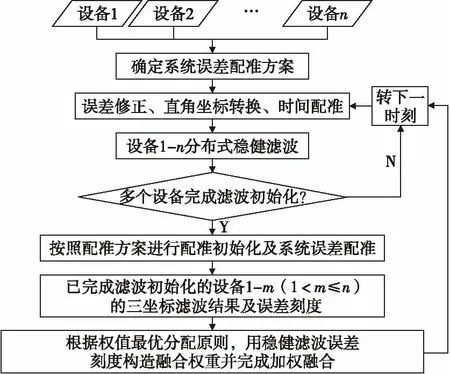
图3 基于稳健滤波残差刻度的加权融合算法流程Fig.3 The distributed weighted fusion algorithm based on robust filtering residual scale estimation

4 测试结果分析

在A、B两雷达参加的某单目标动态测量中，目标大部分航段作匀速直线飞行，部分航段(图4—图7中5 500～7 000航段)作弱机动飞行，A雷达部分航段含连续干扰值，在将两雷达测量数据转至同一直角坐标系并配准后，用本文方法对两雷达数据进行稳健滤波和加权融合测试。

将本文方法对A雷达的滤波结果与卡尔曼滤波进行比较(分别采用匀速模型和当前统计模型卡尔曼滤波进行对比，匀速模型卡尔曼滤波中，过程噪声Q分别取1，9，20倍的Q0，Q0为一确定过程噪声)，并以更高精度的GNSS测量数据作为相对真值，得到滤波融合测试结果。

结果显示(表1，图4—图6)，与卡尔曼滤波相比，本文方法滤波结果受粗差的影响较小，具有较高的样本崩溃点。在将滤波样本容量设为39时，本文稳健滤波方法能够滤除长达15的连续干扰值。

在对A雷达含干扰段数据的滤波测试中，匀速模型卡尔曼滤波发生了视在发散，其中图4(b)，(c)，(d)的滤波发散是由于量测噪声偏离假定模型(粗差)引起的，图5(b)，(c)，(d)的滤波发散是由于弱机动航段系统状态偏离假定模型引起的，两种情形下滤波发散程度均受所设定过程噪声的影响。当前统计模型卡尔曼滤波对机动段处理结果较好(图4(e),图5(e)中5 500～7 000航段)，但当遇到连续粗差时，处理结果较差(容易将连续干扰值判为机动)。

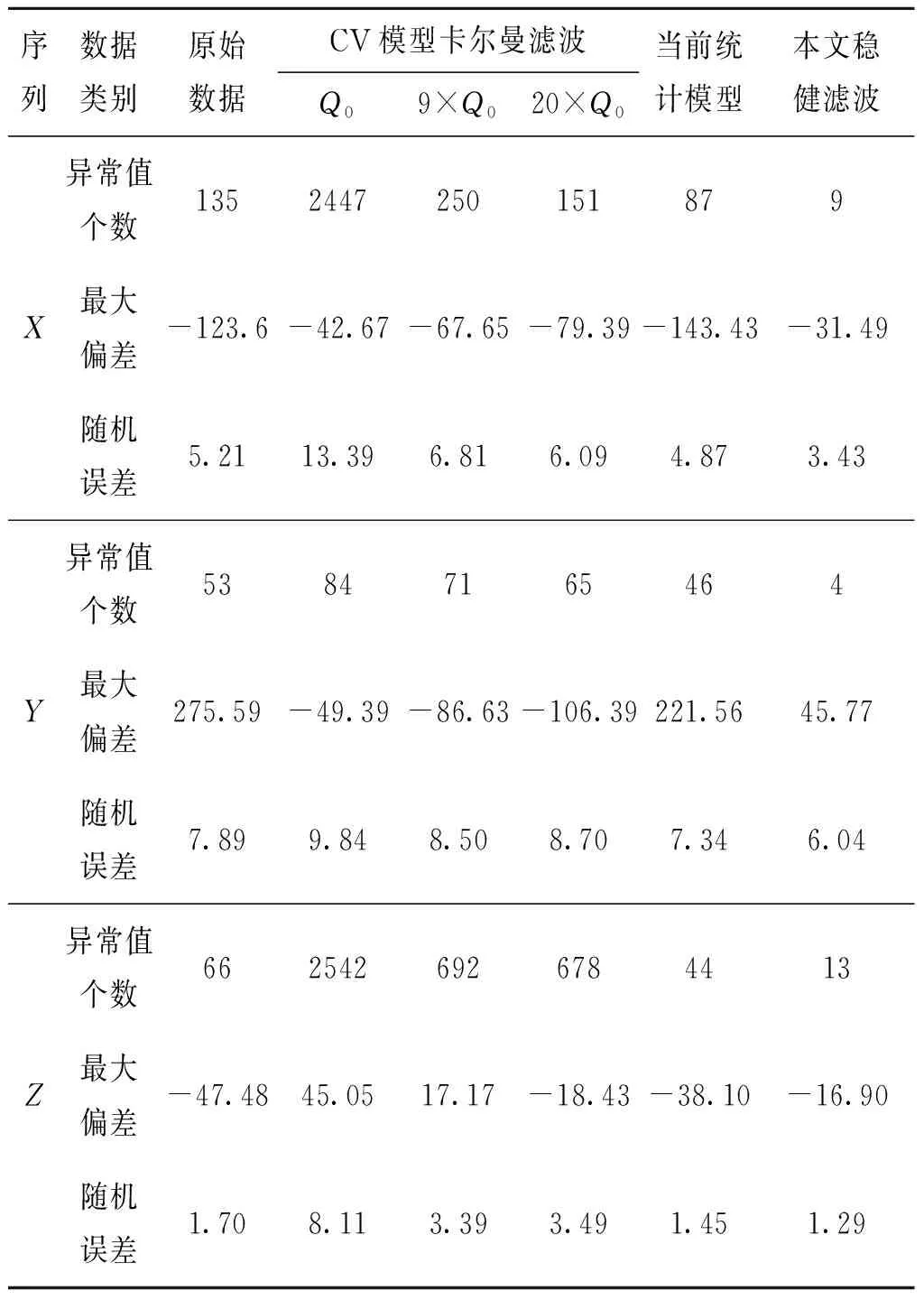
表1 A雷达含干扰航段滤波测试有关数据Tab.1 Relevant data in the filtering test of the disturbed measurement data of radar A

可见，由于卡尔曼滤波需要确知状态方程，并受过程噪声、量测噪声的影响[14]，在复杂电磁环境下的电子信息装备测量数据处理工作中，当卡尔曼滤波假定模型与测量数据真实模型不相符时，滤波效果受到较大影响。

在弱机动条件下，本文滤波方法也具有一定的机动滤波能力，在目标作弱机动前后仍是有效的(图6(a)，(b)，(c)，(d)，图4(f), 图5(f))；同时加权融合测试也达到了较好的稳健效果，融合结果受粗差影响较小(图7)。

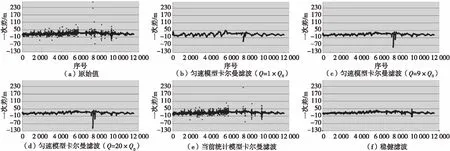
图4 A雷达Y方向滤波前后的一次差Fig.4 Error of Radar A in Y direction before and after filtering

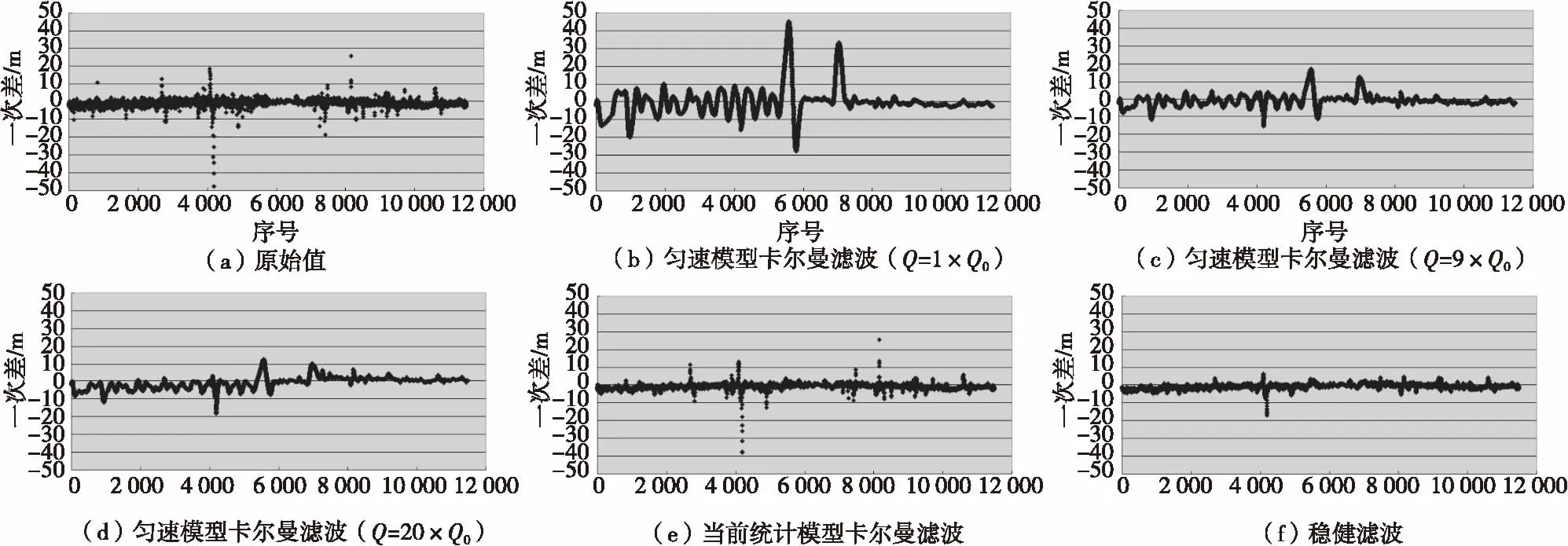
图5 A雷达Z方向滤波前后的一次差Fig.5.Error of Radar A in Z direction before and after filtering

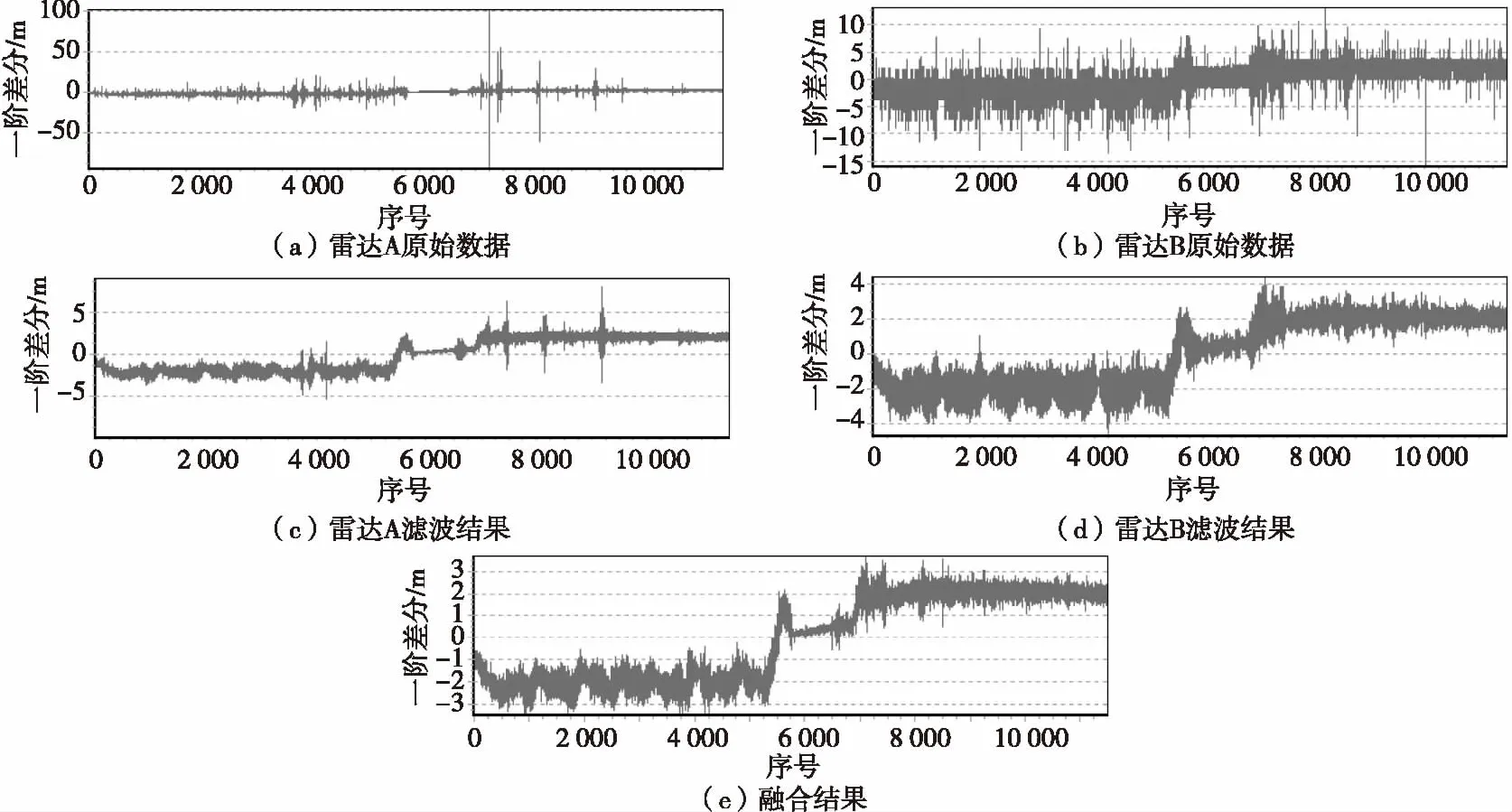
图6 两雷达某测量序列滤波融合前后的一阶差分Fig.6 The first difference of a certain measurement sequence before and afterdata processing

5 结论

本文提出了基于实时中值估计的分布式稳健滤波融合方法，该方法以稳健统计理论为基础，针对电子信息装备多源测量数据加权融合中的复杂电磁环境干扰和传统方法的不稳健性，给出基于实时中值估计和匀速模型的稳健滤波方法，并将稳健滤波残差刻度应用于权值最优分配原则下的融合权重动态计算，最终得到稳健加权融合结果。

典型运动目标实测数据测试结果表明，本文方法具有较高的样本崩溃点，能有效处理含一定长度连续粗差的测量数据，且能用于弱机动情形。与卡尔曼滤波采用最小均方误差为估计准则相比，本文滤波方法所包含的的中值估计属于稳健估计，这也是本文滤波方法相较卡尔曼滤波更具稳健性的根本原因。由于本文方法是在标量(或解耦)意义下针对匀速直线运动目标位置数据得到的，所以在以下条件下是通用的：测量数据为等周期时间序列；状态方程近似于匀速模型，或当系统状态模型与匀速模型发生偏离时，偏离应较小或较慢，以确保过程噪声的影响小于量测噪声的影响。在上述条件下，本文方法有以下特点：样本崩溃点较高，能够滤除干扰等因素造成的连续野值；无需精确的状态方程、过程噪声、量测噪声等先验统计信息；滤波过程实现了对量测噪声的自适应。

当然，本文对稳健滤波融合方法的研究还不够充分，给出了一种匀速模型和标量(或解耦)意义下的稳健滤波融合方法，作者将在以后的工作中结合其他稳健方法开展进一步研究。