偏差仿真中排列组合单步递推算法

刘 峰

（中国运载火箭技术研究院研究发展中心，北京，100076）

0 引 言

飞行器研制过程如图1所示，通常采用六自由度仿真试验考核飞行器控制系统的性能，通过遍历飞行器偏差模型前几项的极限工况，评估偏差项对系统性能的影响程度，找出影响的主要因素。当偏差项有序关联时，需要通过选排列方式遍历偏差模型的前几项，当偏差项相互独立时，只需要通过组合方式遍历偏差模型的前几项。

传统上的排列组合遍历方法中[1,2]，特别是组合遍历，采用傅克慎[3]法的具有较高的运算效率，但生成的组合遍历序列不具备有序性。赵天玉[4]法体现了递归思想，给出了组合构造与序号的函数对应关系，但全面的构造有损运算效率；王孙安等文献[5～8]给出了组合遍历的算法研究与应用实例。

图1 飞行器控制系统六自由度仿真试验设备示意Fig.1 Six Degree of Freedom Simulation Test Equipment for Aircraft Control System

本文提出多种遍历算法，分别为全排列遍历和组合遍历的序数解析算法和单步递推算法，从形式上采用序数解析方式或单步递推方式便于不同遍历的相互嵌套应用，生成的组合遍历序列具备有序性，基于运算量优选得到全排列遍历和组合遍历的单步递推算法，遍历序列有序，有利于事后开展偏差因素影响对比分析等工作。

1 排列组合算法原理

1.1 排列组合基本公式

由《数学手册》第1.1节[1]和《实用数学手册》第1.3节[2]可知，从n个不同的元素中，每次取出n个不同的元素，按一定的顺序排成一列，称为全排列，其排列种数为

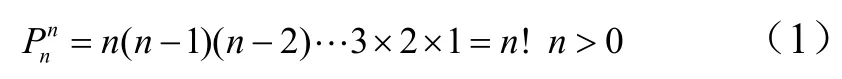
从n个不同的元素中，每次取出k个不同的元素，不管其顺序合并成一组，称为组合，其组合种数为不同的元素，按一定的顺序排成一列，称为选排列，其排列种数为

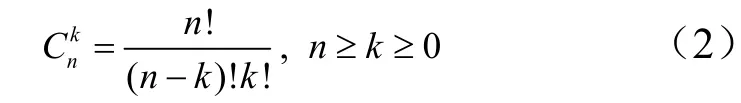
从n个不同的元素中，每次取出k个

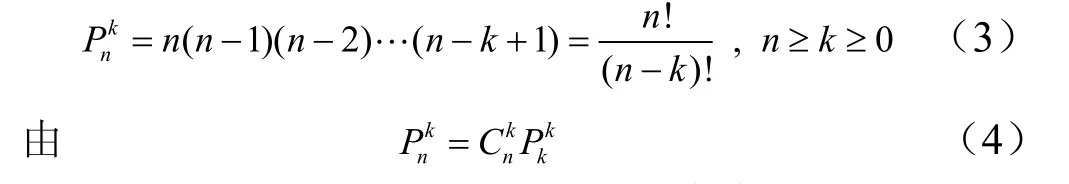
可知，选排列可以表示成组合下嵌套全排列。

1.2 全排列遍历的序数解析

在交换实现排列中，在从1～n的基本整数序列的基础上，根据商数序列调整基本整数序列中数据项的位置，实现当前排列序列。当商数序列的当前值为零时，表示将基本整数序列当前下标的非零值移到排列序列的对应位置，基本整数序列的当前值为零时，自动向后搜索，在移动后将基本整数序列的被移动值清零；当商数序列的当前值为正i时，表示将基本整数序列当前后第i个下标的非零值移到排列序列的对应位置，基本整数序列的当前值为零时，自动向后搜索，以此类推，得到商数序列d，使得：在移动后将基本整数序列的被移动值清零。

全部移动完毕后，基本整数序列被全清零，得到的排列序列即为序数解析后对应全排列遍历中某一特定的排列。

1.3 组合遍历的序数解析

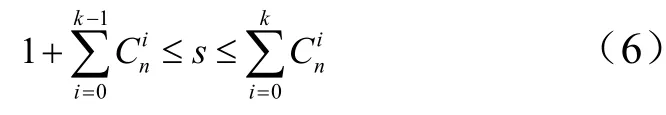
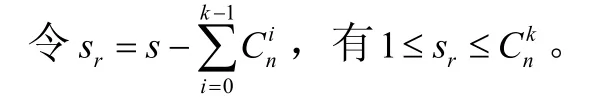
在确定分支中，按照杨辉三角将数据分解为路径，确定左右支路，左小右大，则左支路取1、右支路取0。根据组合递推计算公式有

通过左右支路向上遍历到杨辉三角的顶部后，得到的组合序列即为序数解析后对应组合遍历中某一特定的排列。

1.4 单步递推中关于整数序列的名词解释

全排列遍历或组合遍历中，首先生成整数序列，从左到右，该序列的左端第 1项称为首项或左端项，左端第2项称为次项，右端第1项称为末项或右端项；在搜索过程中，当前搜索索引对应项称为当前项，邻近当前项的左侧第 1项称为左侧项，邻近当前项的右侧第1项称为右侧项。

1.5 全排列遍历的单步递推

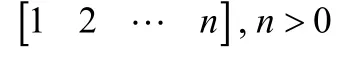
单步递推时，从数列右端向左搜索，若当前项大于左侧项，则停止搜索，完全颠倒从右端项到当前项的所有项的顺序，然后在右端项到当前项序列中找出比左侧项大的最小项，并将其与左侧项交换，由此生成新的序列，作为当前全排列遍历的单步递推结果。

当搜索序列到次项仍不满足当前项大于左侧项的条件，即此时首项大于次项，数列从左到右按照从大到小排列，则单步递推过程中止，循环结束，流程图如图2所示。

图2 全排列单步递推的算法流程Fig.2 Single Step Recursive Algorithm for Full Permutation

1.6 组合遍历的单步递推

单步递推时，从数列右端向左搜索，若当前项大于左侧项，则停止搜索，完全颠倒从右端项到右侧项的所有项的顺序，交换当前项与左侧项，由此生成新的序列，作为当前组合遍历的单步递推结果。

当搜索序列到次项仍不满足当前项大于左侧项的条件，即此时首项与次项均为1，数列从左到右的k项为1，剩余项赋值为0，则单步递推过程中止，循环结束，流程如图3所示。

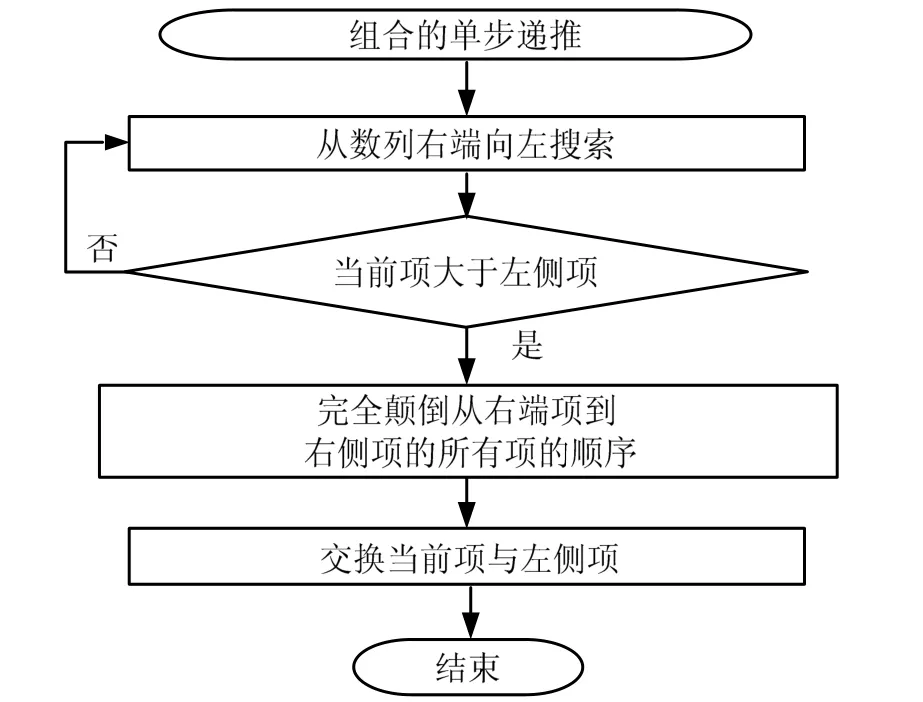
图3 组合单步递推的算法流程Fig. 3 Combined Single Step Recursive Algorithm Flow

全排列遍历和组合遍历的单步递推算法生成的序列存在有序性，故没有重复确保唯一；单步递推算法从递归角度迭代次数符合全排列遍历和组合遍历的性质，故没有遗漏确保完备。

2 排列组合算例推演与分析

2.1 算法的软件开发环境

排列组合遍历算法基于Windows操作系统，采用Visual C++ 6.0（VC6）编译环境和C语言开发，以VC6提供的编译环境进行指令条数统计。为给出直观的可比性，统计Math.h中基本数学函数的指令条数如表1所示（取x=0.618）。计算其全排列序列。首先依次整除4!3!2!1!，得到商数序列A如下：

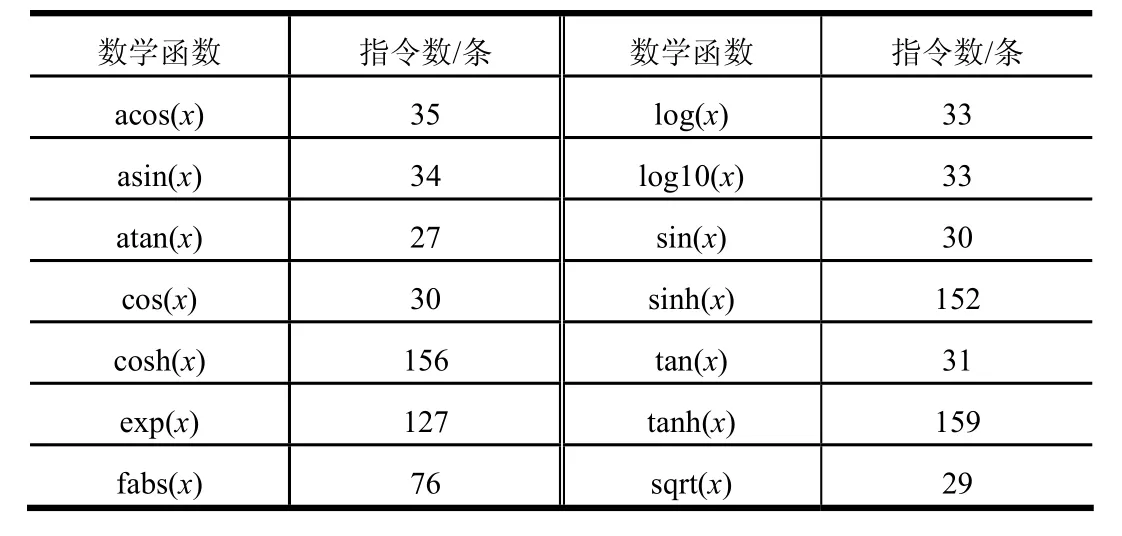
表1 基本数学函数的指令条数Tab.1 Mumber of Instructions for Basic Mathematical Functions

2.2 全排列遍历序数解析的算例

在序数解析时，取n=5时的序数s=59，

第1步：A中第1项为2，则将N中非零首项后的第2项移到P中，原位置清零得到：

式中 ∗表示空位。

第2步：A中第2项为1，则将N中非零首项后的第1项移到P中，原位置清零得到：

依此类推，最后得到目标序列：

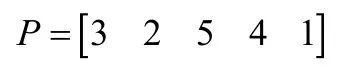
仿真分析可知，软件中生成每个排列的平均指令数为340.00条。

2.3 组合遍历序数解析的算例

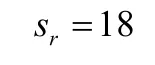
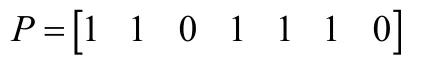
仿真分析可知，软件中生成每个组合的平均指令数为256.68条。

2.4 全排列遍历单步递推算例与统计分析

在单步递推时，取n=5的某一组全排列状态如下：

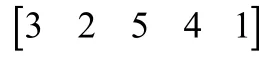
从数列右端向左搜索，当前项5大于左侧项2，停止搜索，有：

完全颠倒从右端项1到当前项5的所有项顺序，有：

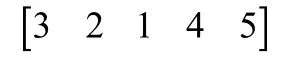
在右端项到当前项序列中找出比左侧项大的最小项4，并将其与左侧项2交换，由此生成新的序列，作为当前组合遍历的单步递推结果如下：

单步递推时，计算 5n=的所有全排列状态的软件指令条数如图 3所示。生成每个组合平均指令数为91.43条。

图4 所有全排列状态的软件指令条数Fig.4 Number of Software Instructions in All Arranged States

在单步递推时，计算不同n工况下的所有全排列状态的软件指令条数如表2所示。

表2 不同工况下全排列状态的软件指令条数Tab.2 Number of Software Instructions in Full Arrangement under Different Working Conditions

从数列右端向左搜索，若当前项1大于左侧项0，得到第1个连续非零的序列，则停止搜索，有：

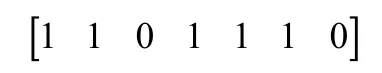
完全颠倒从右端项到右侧项的所有项的顺序，交换当前项与左侧项，由此生成新的序列，作为当前组合遍历的单步递推结果如下：

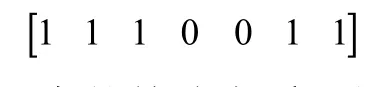
2.5 组合遍历单步递推算例与统计分析

单步递推时，取n=7，k=5某一组组合状态如下：

在完全颠倒顺序的算法中采用折半法可以提高运算效率。

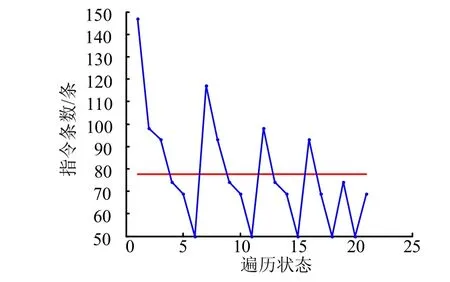
图5 所有组合状态的软件指令条数Fig.5 Number of Software Instructions in AllCombination States

在单步递推时，计算不同n与k组合工况下的所有组合状态的软件指令条数如表3所示。

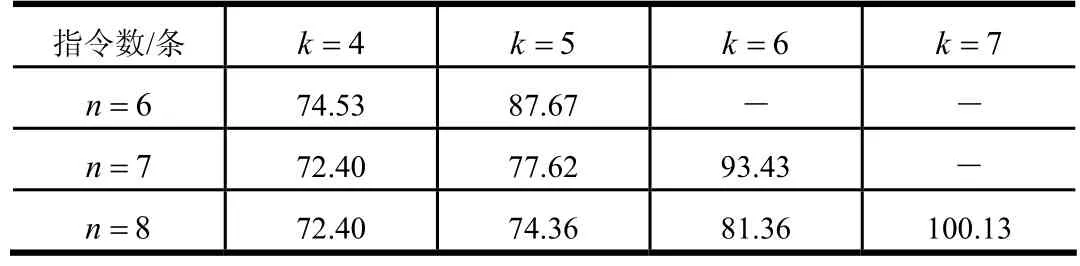
表3 不同组合工况下组合状态的软件指令条数Tab.3 Number of Software Instructions under Different Combination Conditions

2.6 在偏差仿真中的应用

以某飞行器为例，在偏差仿真中共考虑 7n=项偏差，从中随机选择 3k=项进行打靶仿真，则构造初始组合数列如下：

其中，按照顺序的某一位为1时表示选择7项中的某一项，为 0时表示不选，然后可通过单步递推实现偏差项的取舍，从而实现对偏差项的全局遍历。

假设 7项偏差分别为：大气密度、水平风、气动系数、全弹质量、飞行器质量、大气压强和风向角，随机选取3项进行组合遍历的选取状态如图6所示。

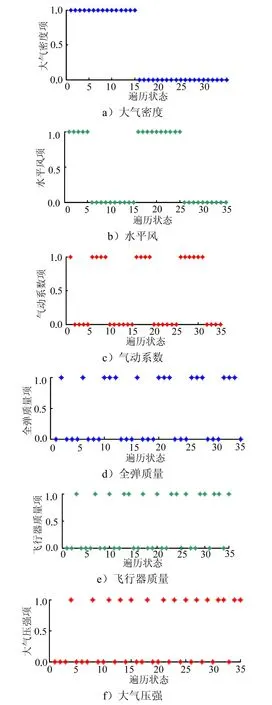
图6 7项偏差下的组合遍历状态Fig.6 Combinatorial Ergodic States under 7 Deviations

续图6

通过带制导的偏差仿真得到组合偏差下热流和动压的最大值如图7所示。

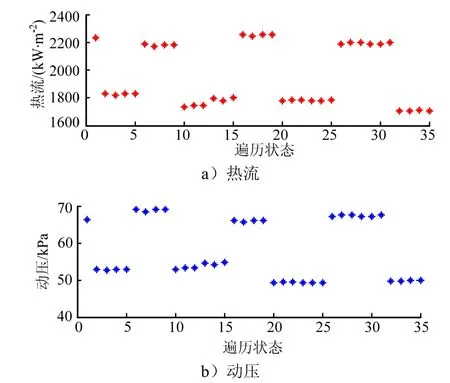
图7 组合偏差下的热流和动压Fig.7 Heat Flow and Dynamic Pressure under Combined Deviations

通过分析可知，气动系数和水平风为影响热流的主要因素，气动系数和大气密度为影响动压的主要因素。取一项偏差进行遍历的结果与极限偏差法等价，组合所有偏差极限工况进行遍历的结果与枚举法等价，而取有限个偏差项进行组合遍历，便于实现运算效率与交叉影响分析之间的均衡。

3 结束语

本文给出了全排列和组合的序数解析算法和单步递推算法，序数解析算法得到的排列组合序列与序数严格对应，意义直观便于使用，只是相比的计算量稍大；单步递推算法的计算量较小，且从算术意义上，可理解为初始化得到量值最低的状态，中止时得到量值最高的状态，单步递推时对序列当前项的左侧项进位，通过颠倒顺序使当前项到右端项的序列获得量值最低的状态，通过单步递推得到的全排列和组合在量值上严格按升幂排列。

此外，对于选排列遍历，可以通过组合遍历中嵌套全排列遍历来实现。通过序数解析算法和单步递推算法，极大方便了与其他形式的遍历方式任意组合，能够应用到飞行器六自由度仿真试验的偏差组合设计等各种离散问题的全局搜索中。