线性弹簧组合式振动时效装置的3次超谐共振特性分析

李俊明， 蔡敢为， 黄院星， 李岩舟

(1. 广西大学 土木建筑工程学院，南宁 530004；2.广西大学 机械工程学院，南宁 530004；3.广西科技大学人事处，广西 柳州 545006；4.广西大学 电气工程学院，南宁 530004)

振动时效(Vibratory Stress Relief， VSR)是一种消除残余应力的方法，实际上是通过振动的形式给工件施加一个动应力，当动应力与残余应力叠加达到或超过材料的屈服极限时[1-2]，工件产生塑性变形而释放应力，有利于提高工件的使用强度、减少变形和稳定精度。特别是在节省时间、能源和费用上具有明显的效果[2-4]。因此在国家倡导节能减排、绿色发展，鼓励工艺技术装备更新改造形势下，进一步研究振动时效技术具有十分重要的意义。

振动时效装置[5]是将一个具有偏心质量的激振器安放在待处理的工件上，通过控制器起动电机并调节其转速使工件处于共振状态[6]，约经20～30 min的振动处理即可达到调整残余应力的目的。振动时效技术适应范围广，从几公斤的小型构件到一、二千吨的海洋平台等大型构件[7-11]。尽管适用范围广，但仍有其局限性。偏心质量激振器虽具有结构简单、造价低、便携、激振力大且可调节等优点，但受其性能限制激励频率范围均在200 Hz以下[12-13]。

大型刚性零件的制备往往会产生很大的残余应力，同时为了保证设备的工作精度，要求这些工件具有较高的刚度，如冶金轧辊、铣床的横梁和立柱等。文中高频率工件是指固有频率大于200 Hz的冶金轧辊、铣床的横梁和立柱等这样高刚度的金属工件。现行的振动时效技术很难消除其残余应力。

为解决高频率工件振动时效问题，研究者提出了工件串(并)联接降频法、悬臂法、振动台法等，这些方法得到的整体系统具有较低固有频率，可以实现在低频率激励下产生共振。在整体系统的振动中，虽然高刚度工件振幅很大，但只是随着整体结构振动作刚体运动，并未发生共振，不会产生振动时效所需要的弹性变形和动应力。因此，这些方法难以取得预期效果。

蒋刚等[14-15]提出并研究了一种高频振动时效。从微观角度分析[15]，高频振动时效是指通过外界输入能量使金属原子回到原先的平衡位置上，从而实现晶格畸变减少，残余应力消除。现行的振动时效技术是通过外界输入能量增加材料内部的位错，位错的增殖导致局部塑性变形，释放残余应力。显然两者微观机理不同。

蔡敢为等[16]提出了高固有频率工件的超谐共振式振动时效装置并取得了发明专利。超谐共振式振动时效装置是指由现行的低频率偏心轮机构激振器作用于非线性振动系统，利用非线性系统的超谐共振特性，以接近工件固有频率的响应频率进行激励，从而实现高频率工件主共振。但专利中并未具体提出采用什么类型的非线性系统来有效实现超谐共振式振动时效装置，仍需深入研究。

圆柱不等截距螺旋弹簧、圆锥螺旋弹簧、空气弹簧等非线性弹簧都可以产生非线性振动，但目前利用这类弹簧的超谐式振动时效装置仍很少。即使非线性弹簧可以实现超谐共振，但非线性弹簧制造工艺复杂，非线性参数难控制、不可调节等这些问题限制了超谐共振式振动时效技术满足不同固有频率工件的需要。

线性弹簧按特定方式组合也可以产生非线性特性，比如分段线性弹簧。本文提出利用线性弹簧来实现超谐共振，设计并研究一种线性弹簧组合振动装置，在此基础上就其非线性弹力特性进行分析，应用多尺度理论对其3次超谐共振的振动机理进行探讨。

1 线性弹簧组合式振动时效装置及原理

图1(a)所示线性弹簧组合式振动时效装置，包括1、高频率工件，2、基座，3、激振块，4、偏心质量激振器，5、刚性槽体结构和三个同刚度等长度的弹簧。高频率工件两端刚性固定于基座，三个弹簧一端连接激振块，另外一端固定在基座上。刚性槽体结构与激振块结构如图1(b)，主要约束激振块仅在垂直方向振动。激振器刚性装卡于激振块内，是整个系统的激励来源。含激振器的激振块与三个弹簧组合构成一个线性弹簧组合质量系统。

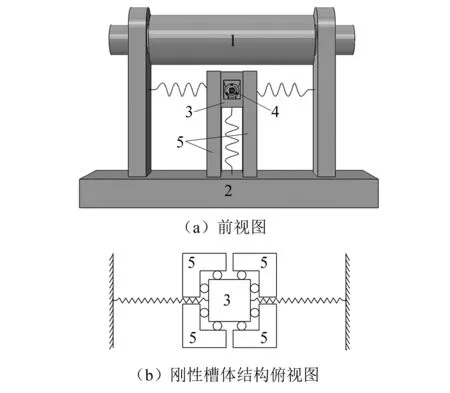
图1 线性弹簧组合式振动时效装置：Fig.1 VSR equipment combined linear springs

受到激振器的激励，激振块在三个弹簧的作用下产生垂直方向的非线性振动，在低频激励下可以响应出3倍于激励频率的高频频率，产生3次超谐共振，激振块以接近工件固有频率的响应频率去激励工件，从而实现高频率工件的主共振。

2 线性弹簧组合质量系统的非线性特性

2.1 非线性弹力

质量为M激振块由三个刚度系数均为K、长度均为L弹簧支承，这里激振块质量M是包含激振器质量在内的总质量。初始状态时，弹簧均保持自然长度，水平方向的两个弹簧与激振块同在一条直线，垂直方向的弹簧垂直此直线。以x为位移，以激振块在静平衡位置为原点，竖直向下为正方向，建立坐标轴，如图2。

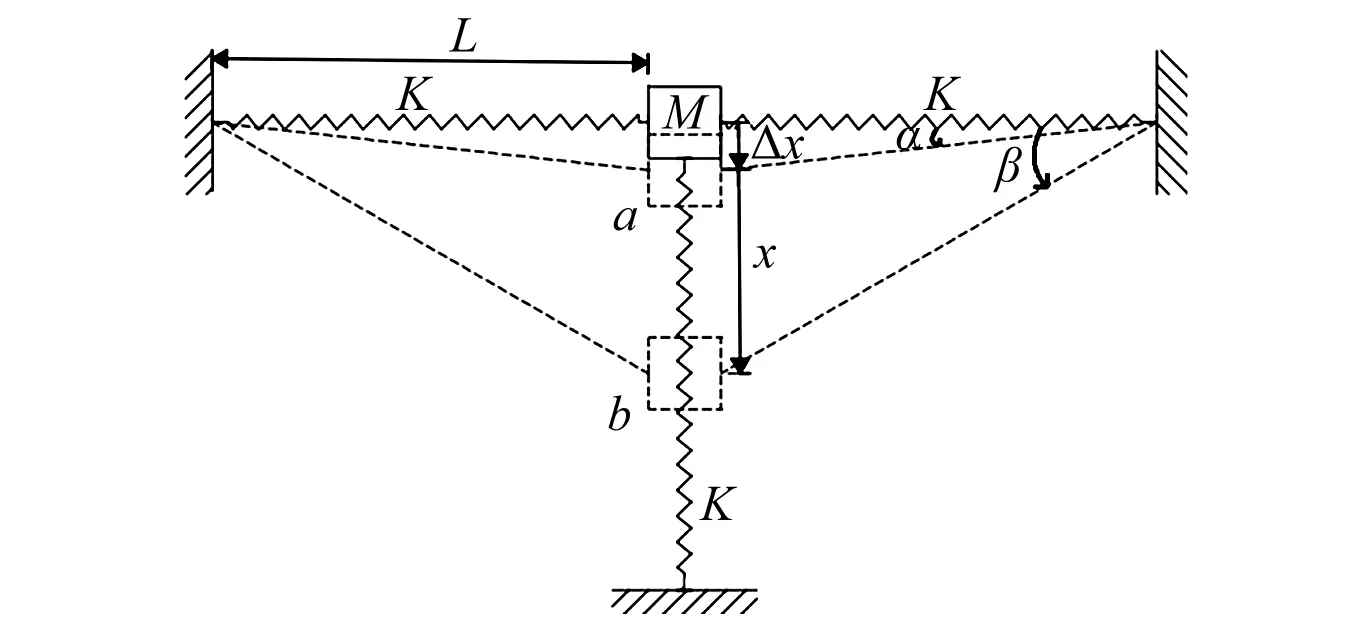
图2 线性弹簧组合质量系统垂直方向振动模型Fig.2 Model of the linear springs combination mass systemvibration in the vertical direction

激振块在重力作用下，会发生微小的位移Δx，在点a处达到静平衡状态，此时水平弹簧与水平方向夹角α。根据静平衡状态，可得

(1)

式中Δ2x=Δx·Δx。

激振块在外力作用下产生一个大位移，在点b处达到平衡状态，此时外力突然消失。结合式(1)，则有

(2)

这里，Fk为指向平衡位置的恢复力。

略去高阶无穷小量后，

(3)

静平衡状态时，激振块只发生了微小位移Δx≪L，Δx→0，所以式(3)等价于

(4)

综上可知，水平方向两个弹簧对质量块的作用力始终保持大小相等，方向相反；垂直方向的恢复力是非线性的。这是非线性弹力的理论基础。

2.2 固有频率

质量为M激振块由三个弹簧支承，并处于静平衡位置，如图3所示。这里的激振块的质量M含激振器质量的总质量，弹簧为仅具有刚度的无质量弹簧，且K1=K2=K3=K。三个弹簧一端连接激振块，另外一端固定，构成一个线性弹簧组合质量系统，激振块只在平面内作微振动，不存在耗散能力和加进能力的广义力，这是一个保守系统。

图3 线性弹簧组合质量系统Fig.3 The linear springs combination mass system

设l1是激振块M的位移在弹簧K1轴线方向上的投影，对于微振动，可以认为恢复力总沿着原来弹簧轴线方向。令弹簧K1轴线方向的余弦为(cosα,sinα)，则弹簧K1的势能为

(5)

则系统的总势能为

(6)

系统的动能：

(7)

利用朗格朗日方程建立系统的运动微分方程。自由度的拉格朗日方程为：

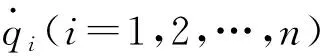
(8)

式中：a11=cos2α+cos2β+cos2γ，

a12=a21=sinαcosα+sinβcosβ+sinγcosγ，

a22=sin2α+sin2β+sin2γ。

根据2.1的讨论可知，静平衡时可取α=0，β=180，γ=270，可得

(9)

设主振动为

(10)

式中：ω0为系统振动的固有频率。φ1,φ2为振幅，φ为相位角。代入方程(9)，得

特征方程为

(11)

由此解出

(12)

式中ω01,ω02为系统振动的固有频率。

相应的主振型可取为

(13)

说明系统以第一阶固有频率振动时只作沿着x2方向即垂直方向振动，且不产生x1方向即水平方向振动。证明图1所示的线性弹簧组合式振动时效装置的合理性和有效性。

2.3 3次超谐共振

图4所示是一个包含偏心质量激振器的线性弹簧组合质量系统的力学模型，设含激振器的激振块总质量为M，激振器的偏心质量为m，偏心距是e，转子的角速度为ω，弹簧刚度系数均为K、长度均为L。

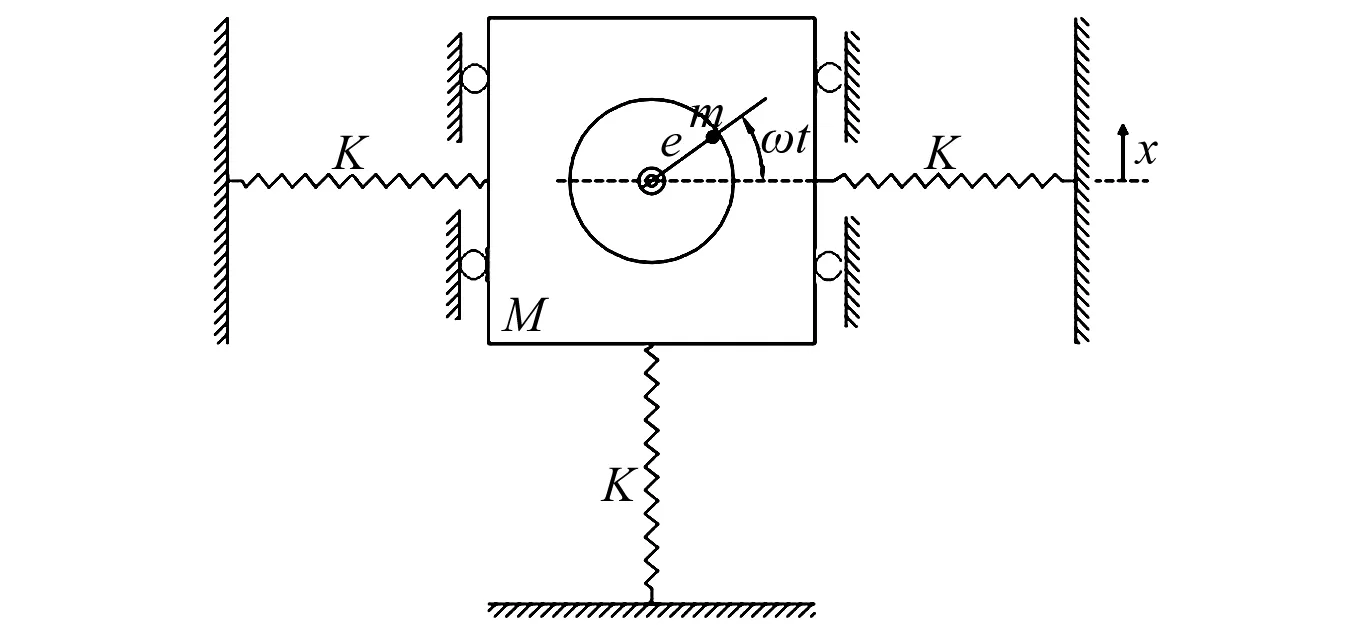
图4 线性弹簧组合质量系统的力学模型Fig.4 The linear springs combination mass system mechanical model

用坐标x表示质量块离开平衡位置的垂直位移，根据达朗伯原理得到系统在垂直方向的运动微分方程为：

(14)

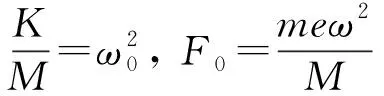
(15)

则方程(15)可写为

(16)

采用多尺度法讨论非线性振动的近似解，设方程式(16)一次近似解为

x(t,ε)=x0(T0,T1)+εx1(T0,T1)

(17)

式中：T0=t，T1=εt表示不同尺度的时间变量。

设Di=∂/∂Ti,(i=0,1)，将方程式(17)代入方程式(16)，令等式两端ε0和ε1的系数相等，可得

(18)

(19)

设方程式(18)的通解的复数形式为

(20)

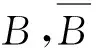
(21)

式中：cc表示其左边各项的共轭复数。

根据非线性振动理论[17-18]，方程式(21)的右边各项中，不仅含eiω0T0，还含有ei(2ω0-ω)T0，e3iωT0,eiωT0项，当3ω≈ω0时产生的共振称为超谐共振。

为了说明线性弹簧组合质量系统3次超谐共振响应特性，选取一组基本参数：含偏心质量激振器质量块总质量M=0.046 2 t，其中激振器的偏心质量m=0.015 6 t，偏心距e=150 mm，弹簧刚度系数均K=96 035 N/mm,材料密度ρ=7.8×10-9t/mm3，弹性模量E=210 000 MPa，泊松υ=0.3。

根据方程式(12)可得线性弹簧组合质量系统的固有频率ω0=229.58 Hz，系统在简谐激励下的响应如图5～6。可见，当激励频率ω=ω0=229.58 Hz时，系统的振幅随时间无限增大即共振时的振动响应，如图5。当激励频率ω=76.53 Hz≈ω0/3时，系统的响应中包含3ω频率的振动，产生了3次超谐共振响应，最大位移约8.4 mm，如图6。

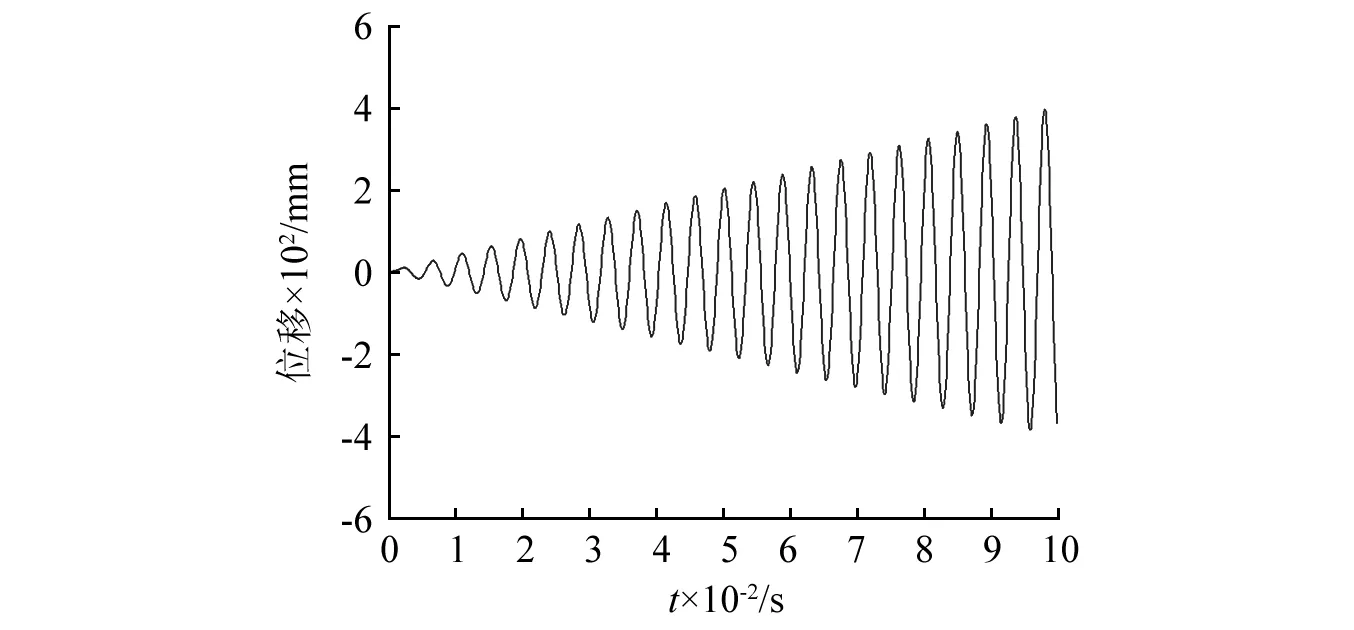
图5 ω=229.58 Hz响应图Fig.5 Time-displacement response for ω=229.58 Hz

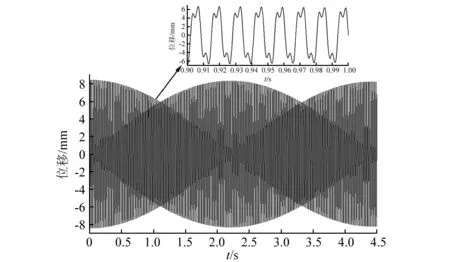
图6 ω=76.53 Hz响应图Fig.6 Time-displacement response for ω=76.53 Hz

3 案例与讨论

以∅920 mm×3 000 mm冶金轧辊(图7)作为振动时效处理的工件，选取一组轧辊基本参数：材料密度ρ=7.8×10-9t/mm3，弹性模量E=210 000 MPa，泊松比v=0.3。振动时效装置如图1，借助ABAQUS软件仿真获得轧辊的固有频率为ω0=229.58 Hz。激振块(含激振器)总质量选取M=0.462 t，通过控制器起动激振器并调节其转速ω=76.53 Hz≈ω0/3，轧辊在激振块激励下，振幅、动应力响应，如图8～11。

图7 轧辊结构尺寸(mm)Fig.7 Structure sizeof the roll(mm)

根据图6，激振块3次超谐共振产生位移较小，初始状态时可保持激振块与轧辊接触但不存在相互作用，两者的初始位移和初始速度都为零。振动过程中，激振块与轧辊分为接触阶段和非接触阶段。接触阶段，在激振块激励下轧辊发生强迫振动，其响应是自由伴随振动和稳态振动的叠加；非接触阶段，轧辊进行自由振动。接触振动主要发生在正向位移，非接触主要发生在负向位移，正向位移值大于负向位移值主要是正向振动中存在激振块与轧辊碰撞激励造成，如图8所示。

振动初期，轧辊在激振块的激励下开始振动，所以振动初期主要表现为过渡阶段的强迫振动响应。轧辊与激振块分离后，进行自由振动且振幅随时间逐渐增大，振动周期更加明显，从图8可以看出，T≈0.004 36=1/229.58。

图9中229.58 Hz的幅值很微弱，76.53 Hz出现明显峰值。因为振动初期，激振块在激振器激励下，3次超谐响应还不明显，但随着时间增加，图10可以看到，229.58 Hz出现明显峰值，幅值显著增大，76.53 Hz振幅减弱。

选择轧辊辊面一条母线为对象，其上各点产生的位移和动应力如图11。沿轧辊长度方向动应力值分布呈中间大、两端小状，与两端固定等截面梁的第一阶振型[19]基本一致。

综合上述分析，轧辊实现了第一阶固有频率的主共振。高刚度轧辊的屈服极限约450～600 MPa，残余应力一般约50～200 MPa，结合图11可知，动应力足够满足振动时效条件达到消除残余应力的目的。

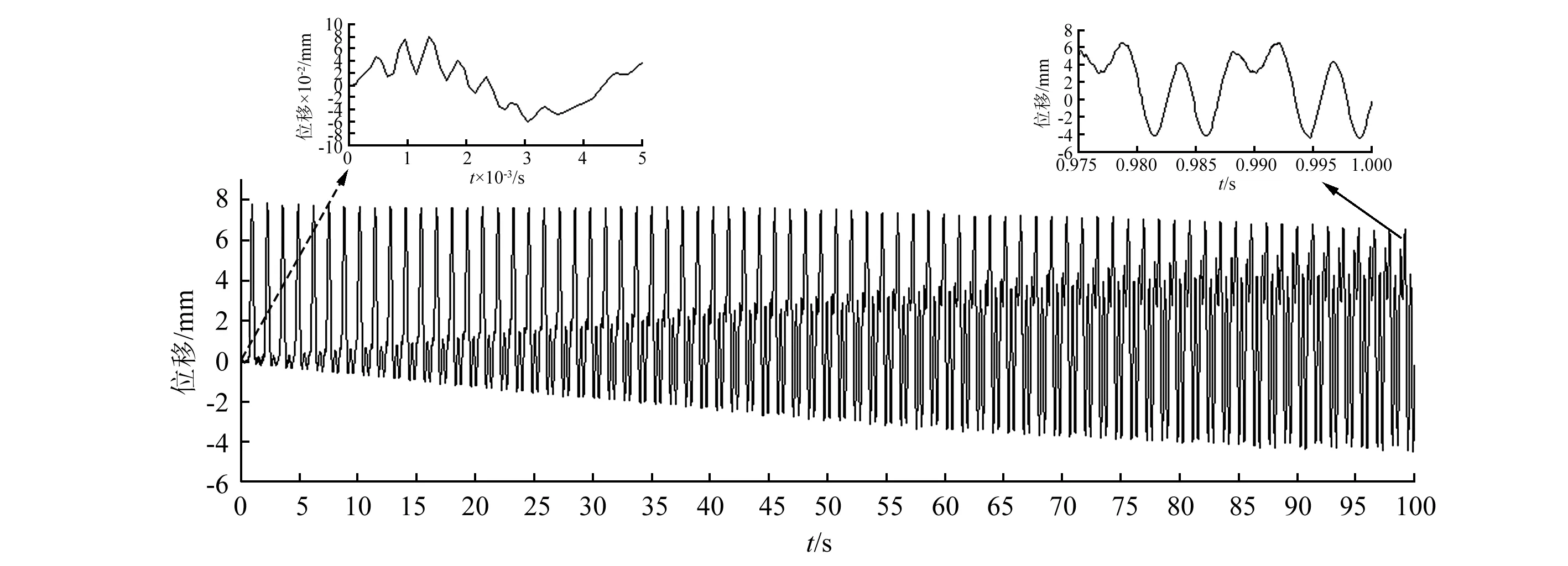
图8 轧辊振幅响应图Fig.8 Time-displacement response of the roll

图9 第0.1 s～0.2 s幅频响应图Fig.9 Amplitude versus frequency response from 0.1 s to 0.2 s

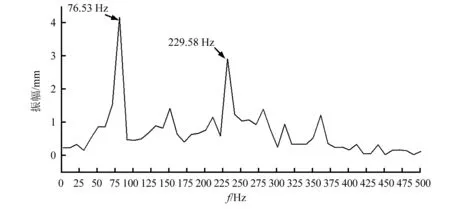
图10 第0.65 s～0.75 s幅频响应图Fig.10 Amplitude versus frequency response from 0.65 s to 0.75 s

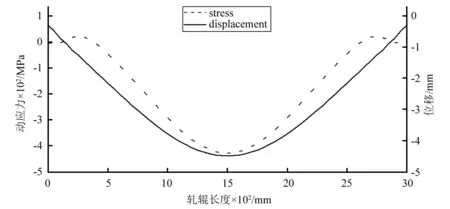
图11 辊面位移、动应力响应图Fig.11 Stress-displacement response along the roll

4 结 论

本文提出的线性弹簧组合式振动时效装置，通过研究发现：

(1)线性弹簧组合质量系统在垂直方向的恢复力是立方形式的非线性力，非线性项系数与弹簧刚度和长度有关。系统在垂直方向振动的固有频率只取决于激振块的质量和弹簧刚度，与弹簧长度无关。

(2)激振块在较低频率激励下，经过三个弹簧组合联合作用，产生3次超谐共振，激振块以其响应的频率激励高频率工件，高频率工件俘获其主共振频率，从而实现共振。

(3)偏心质量激振器是整个振动时效装置的激励来源，为了保证水平方向不受外力扰动，可以采用双轴式惯性激振器，只产生垂直方向的离心力。